2025-09-08
Reflecting
What did I learn today?
Fundamentals of statsicials and thermal physics I
논의 1. 만약 오른쪽으로 갈 확률과, 왼쪽으로 갈 확률이 서로 다르다면? 앞에선 둘다 1/2이었지. 그럼 그냥 식을 이렇게 바꾸면 되는 것 아닌가? 오른쪽으로 갈 확률을 \(p\), 왼쪽으로 갈 확률을 \(q\)라고 하자. \(p+q=1\)이다.
\[\tilde{P}(n_{r}) = \frac{N!}{n_{r}! n_{l}!} p^{n_{r}}q^{n_{l}}\]논의 2. BInomial Distribution을 다 더했을 때, \(n_{r} = 0, N\)까지 다 더했을 떄 1이 나올까? 1이 나와야 \(\tilde{P}(n_{r})\)이 확률이니까.
\[\sum_{n_{r} = 0}^N \frac{N!}{n_{r}!(N-n_{r})!}p^{n_{r}}q^{N-n_{r}}\]다음을 생각해보자.
\[(p+q)^N = (p+q)(p+q)\dots(p+q)\] \[= C_{0}p^0q^N + C_{1}p^1 q^{N-1} + \dots + C_{N}p^N q^0\]이때 계수는 무엇일까? \((p+q)(p+q)\dots(p+q)\)에서 p를 뽑는 개수이다. p를 0번 뽑으면 \(p^0q^N\)의 계수가 될 것이고, p를 2번 뽑는 횟수가 바로 \(p^2q^{N-2}\)의 계수가 될 것이다.
\[= \begin{pmatrix} N \\ 0 \end{pmatrix}p^0 q^N + \begin{pmatrix} N \\ 1 \end{pmatrix}p^1 q^N + \dots + \begin{pmatrix} N \\ N \end{pmatrix}p^N q^0\] \[= \sum_{i}^{N}\begin{pmatrix} N \\ i \end{pmatrix}p^i q^{N-i}\] \[= \sum_{i}^{N} \frac{N!}{i!(N-i)!}p^iq^{N-i}\]\(p+q=1\)이므로, \((p+q)^N\)도 1이다. 따라서 위의 값은 1이다. 그러나 이 값은 Binomial Dist.를 Sum한 것과 동일하다. 따라서 Binomial Dist를 다 더하면 1이다. QED.
논의 3. avarage, mean, expectation value, variance, k-th moment 평균 또는 기댓값은 다음과 같이 표기한다.
\[\langle m \rangle = \bar{m} = \sum_{m} m P(m)\]분산은 평균으로부터 얼마나 떨어져있는지를 나타내는 척도이다.
\[\Delta m = m - \langle m \rangle\]이것의 평균은 다음과 같다.
\[\langle \Delta m \rangle = \langle m - \langle m \rangle \rangle\]평균 기호는 선형성이 존재한다.
\[= \langle m \rangle - \langle m \rangle = 0\]편차의 평균은 항상 0이므로 의미없다. 따라서 제곱의 평균을 사용한다.
\[\langle( \Delta m)^2 \rangle = \langle (m - \langle m \rangle)^2 \rangle\] \[= \langle m^2 - 2m\langle m \rangle + \langle m \rangle^2 \rangle\] \[= \langle m^2 \rangle - 2 \langle m \rangle \langle m \rangle + \langle m \rangle^2\] \[= \langle m^2 \rangle - \langle m \rangle^2\]편차의 제곱을 알기 위해선, random variable 제곱의 평균 값이 필요하다.
평균과 분산만으로는 정규분포를 기술하기 충분하지만, 일반적인 확률분포를 기술하기는 충분하지 않다. 얼마나 퍼져있냐 뿐만 아니라, 퍼져있는 모양은 또 어떠한가? 이는 분산만으로는 다 알 수 없다. \(\langle (\Delta m )^3 \rangle\) 이 필요할 수 있고, 편차의 4승 제곱이 필요할 수 있다. 이를 알기 위해선 각각 3제곱의 평균, 4제곱의 평균이 필요하다. 가장 일반적으로, k제곱의 평균 식을 알고 있다면 우리는 확률분포를 정확히 알고있는 것과 같다. \(\langle (\Delta m)^k \rangle\)를 알기 위해선 다음 정보가 필요하다.
\[\langle m^k \rangle\]이를 k-th moment라고 한다.
이걸 어떻게 알 수 있을까? characteristic function로 알 수 있는 방법이 있다. 이것이 무엇인가? 복소함수의 평균이다.
\[\Phi(\theta) = \langle e^{i\theta m} \rangle = \sum_{m}e^{i\theta m}P(m)\][!question] 왜 \(\langle m^2 \rangle = \sum_{m^2} m^2 P(m^2)\)이 아니라, \(\sum_{m}m^2 P(m)\)일까?{title} 이건 \(m^2\)의 평균을 구하는 것이지. \(m^2\)의 확률은 \(m\)의 확률과 대응되기 때문에 \(P(m)\) 확률을 사용해도 되는 것이다.
같은 논리로, \(e^{i\theta m}\)의 확률은 \(m\)의 확률과 대응되기 때문에 \(P(m)\)을 사용한다.
\(e^x\)를 테일러 전개하면 어떻게 되더라? 테일러 전개가 무엇이었지? 아이디어는 임의의 함수 \(f(x)\)를 다항식 \(1 + x + x^2 + x^3 + \dots\)이라는 무한차원 기저로 표현하는 것이다. 또는, 함수의 local 정보를 알고있을 때 이를 global range로 확장할 때 사용 가능하다. 이때 계수는, \(f(x)\)의 도함수와 차수로 나눈 값을 사용한다.
\[f(x) = f(0) + \frac{f'(0)}{1!}x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + \dots\]\(e^x\)를 전개하면 다음과 같다.
\[e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots\]따라서 다음과 같다.
\[\Phi(\theta) = \sum_{m}e^{i\theta m}P(m)\] \[= \sum_{m}\left( 1 + i\theta m + \frac{(i\theta)^2}{2!}m^2 + \dots + \frac{(i\theta)^k}{k!}m^k +\dots \right) P(m)\]여기서 \(m^k\)만 남기려면, \(\Phi(\theta)\)를 \(\theta\)에 대해 \(k\)번 미분하고, 미분하고 남은 뒤에거는 \(\theta\)에 0을 넣으면 된다! k번 미분하면, \(m^k\)의 계수는 \(k!\)는 상쇄되며, \(i^k\)항만 남는다. 즉, 다음과 같다.
\[\frac{1}{i^k}\frac{d^k\Phi(\theta)}{d\theta^k} \mid _{\theta=0} = \sum_{m}m^kP(m) = \langle m^k \rangle\]\(\Phi(\theta)\)를 알고있다면, k-th moment를 구할 수 있다. 그렇다면, \(\Phi(\theta)\)가 무엇인가? \(\Phi(\theta)\)에서 주어져야할 것은 \(P(m)\)이다. binomial dist의 경우 \(P(m)\)이 알려져있다.
\[P(m) = \tilde{P}(2n_{r} - N) = \frac{N!}{n_{r}!(N-n_{r})!} p^{n_{r}}q^{N-n_{r}}\]따라서 다음과 같다.
\[\Phi(\theta) = \sum_{m}e^{i\theta m} P(m)\] \[= \sum_{m}e^{i\theta m} \left( \frac{N!}{n_{r}! (N-n_{r})!} \right)p^{n_{r}}q^{N-n_{r}}\] \[= \sum_{m}e^{i\theta (2n_{r} - N)} \left( \frac{N!}{n_{r}! (N-n_{r})!} \right)p^{n_{r}}q^{N-n_{r}}\] \[= e^{-Ni\theta} \sum_{m} \left( \frac{N!}{n_{r}! (N-n_{r})!} \right) e^{2i\theta n_{r}} p^{n_{r}}q^{N-n_{r}}\] \[= e^{-Ni\theta}\sum_{m}\left( \frac{N!}{n_{r}! (N-n_{r})!} \right)(pe^{2i\theta})^{n_{r}}q^{N-n_{r}}\] \[= e^{-Ni\theta}(pe^{2i\theta} + q)^N\] \[= (pe^{i\theta} + qe^{-i\theta})^N\]즉, \(P(m)\)을 알면 \(\Phi(\theta)\)를 알 수 있고, 이를 알 수 있다면 \(\langle m^k \rangle\)를 알 수 있다. k-th moment를 알면 확률분포를 전부 알고있는 것과 같다.
평균을 구하려면 \(k=1\)를 넣으면 된다. 분산을 구하려면 \(k=2\)를 넣으면 된다.
\[\langle m \rangle = \frac{1}{i}\frac{d\Phi(\theta)}{d\theta}\mid _{\theta=0}\] \[= \frac{1}{i} N (\dots)^{N-1}(ipe^{i\theta} - iqe^{-i\theta})\mid _{\theta=0}\] \[= N(p - q)\]variance는 무엇인가?
\[\langle m^2 \rangle = \frac{1}{i^2} \frac{d^2\Phi(\theta)}{d\theta^2}\mid _{\theta=0}\] \[= - \frac{d}{d\theta}(N(\dots)^{N-1}(ipe^{i\theta} - iqe^{-i\theta}))\mid _{\theta=0}\]뒤에를 미분하면 \(ipe^{i\theta}(i) - iqe^{-i\theta}(-i) = -pe^{i\theta} - qe^{-i\theta}\)와 같다.
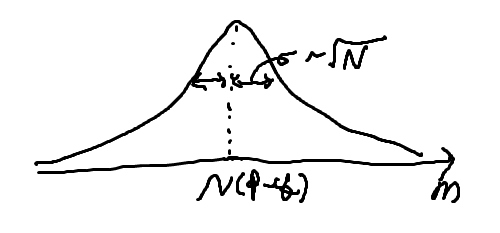
\[= - N(N-1)(\dots)^{N-2}(ipe^{i\theta} - iqe^{-i\theta})^2 - N(\dots)^{N-1}(-pe^{i\theta} - qe^{-i\theta})\mid _{\theta = 0}\] \[= -N(N-1)(-1)(p-q)^2 - N (-1)\] \[= N(N-1)(p-q)^2 + N\] \[\langle (\Delta m)^2 \rangle = \langle m^2 \rangle - \langle m \rangle^2\] \[= N(N-1)(p-q)^2 + N - N^2(p-q)^2\] \[= - N(p-q)^2 + N\] \[= N(1 - (p-q)^2)\] \[= N((p+q)^2 - (p-q)^2)\] \[= 4Npq\]표준편차는 \(\sqrt{ 4Npq }\)와 같고, 우리는 N이 아보가르도수만큼 큰 거시 Case에 관심이 있다. 때문에 \(\sqrt{ N }\) 정도로 근사한다. 정규분포 그래프를 그려볼 수 있는데, 만약 N이 아보가르도수만큼 크다면? 오차율이
\[\frac{\sqrt{ \langle (\Delta m)^2 \rangle }}{\langle m \rangle} \simeq \frac{1}{\sqrt{ N }} = 10^{-12}\]와 같다. 즉 평균값에 비해 표준편차 값은 매우 작은 값이다. 따라서 거시적인 스케일에선 분포가 다음과 같이 보일 것이다.
때문에 위치가 결정된 것 처럼 보인다. 그러나 N이 작아져, 미시적인 스케일로 들어가면, 위치는 확률로써 기술된다는 Concept이다.
Improve:
끌려다니지 않고, 내 삶을 주도하자.
Thanks:
좋은 기숙사에서 살고 있는게 감사하다.
Emotion:
초조, 여유가 없음. 여유롭게, 긍정적이게.