컴퓨터그래픽스 7. Vertex Processing이 무엇인가 - Affine Space
Vertex Processing이 무엇인가?
Vertex Processing이란 한마디로, Local Coordinate로 기록된 Vertex 좌표를 Clip Space 위의 좌표로 옮겨주는 과정이다. 이 과정을 어떻게 해야할까?
(1) Model Transform 먼저, 오브젝트의 중심점을 기준으로 상대적으로 기록되어있던 좌표를 Local Coordinate라고 한다. 하지만 실제로 오브젝트는 어디에 위치해있는가? Scene 위에 절대 좌표계에 위치한다. 이를 World Coordinate라고 한다. 따라서 가장 먼저 Local Space 위의 Vertex 좌표를 World Space 위로 옮겨야 한다.
(2) View Transform 우리가 실제로 보는 화면은, 카메라가 보는 화면이다. 카메라가 보는 시점을 만들려면, 카메라 기준의 좌표계로 Vertex를 옮기고, 카메라의 시야만큼 Cliping 하면 되지 않을까? 따라서, World Space 위의 Vertex를 View Space (Camera Space)로 옮기는 작업을 해야한다.
(3) Projection Projection은 Viewing Volume을 View Plane 위에 투영하거나, Normalized Viewing Volume 위로 투영하는 방법이 있다. View Plane에 투영하는 방법은 Normalized 과정이 없으므로, 일관된 스크린을 얻지 못한다. 따라서 Normalized Viewing Volume 위로 투영하는 방법을 사용한다.
Projection까지 거치면 Local Space 위에 있던 Vertex가 4차원 Clip Space 으로 변환된다. 여기까지가 Vertex Processing에서 담당하는 작업이다. 이후엔 Vertex는 Cliping, Backface Culling을 거쳐 NDC 공간으로 변환된다. 이후 Z-Test를 거쳐 Viewport 좌표로 이동하면 최종적으로 Frame Buffer에 들어가는 정보가 생성된다.
어떻게 변환하는가?
변환을 알아보기 전에, 다음 개념을 명확히 잡을 필요가 있다. Vertex는 벡터인가? 벡터란, 크기와 방향을 갖는 양이고, 그 위치는 중요하지 않다. Vertex를 벡터로 인식하면, Vertex의 위치는 의미가 없는 정보가 된다. 그러나 Vertex는 위치 정보가 중요하다. 따라서, 벡터 뿐만 아니라 위치라는 새로운 Concept이 필요하다.
위치를 어떻게 정의하는가?
Affine Space를 정의한다. Affine Space란, 벡터 공간에 ‘점 (Point)’ 요소를 추가한 공간이다. 점은 \((x, y, z)\)이고, 벡터는 \((a, b, c)\)이다. 점과 벡터를 구분할 수 없다! 이 문제를 해결하기 위해 Homogenous Coordinate를 도입한다. 마지막 값에 점은 1, 벡터는 0으로 다른 값을 주면 둘을 구분할 수 있다.
\[\text{Point} \equiv (x,y,z, 1)\] \[\text{Vector} \equiv (a,b,c,0)\]아핀 공간 위의 Point는 공간위의 위치, 한 점을 의미한다. 아핀 공간 위의 Vector는 크기와 방향을 가진 양이다. Point와 Vector 사이의 Operator 또한 자연스럽게 정의할 수 있다.
- Vector + Vector = Vector
- Vector + Point = Point + Vector = Point
- Point - Point = Vector
- Point + Point = 정의 불가!
점과 점의 덧셈을 정의할 수 없는 이유는, 마지막 성분이 0 또는 1이 아니기 때문이다. 만약 마지막 요소가 1이 되도록 점을 더할 수 있으면, 점과 점의 덧셈을 정의할 수 있지 않을까?
\[\lambda_{1} P_{1} + \lambda_{2} P_{2} = P\] \[\implies \lambda_{1}(P_{1}, P_{2}, P_{3}, 1) + \lambda_{2}(P_{1}, P_{2}, P_{3}, 1) = (\lambda_{1}P_{1} + \lambda_{2}P_{2}, ~\dots, ~\lambda_{1} + \lambda_{2})\]만약 \(\lambda_{1} + \lambda_{2} = 1\)이면, 점 \(P\)의 마지막 요소값은 반드시 1을 만족한다. 이런 방식으로 여러 점을 더하는 방법을 Affine Combination (아핀 조합, 아핀 결합)이라고 한다. 아핀 조합은 일반적으로 다음과 같이 정의된다.
\[\sum_{i \in I}\lambda_{i}P_{i}, ~~~\sum_{i \in I} \lambda_{i} = 1\]이때 \(P_{i}\)는 한 Point, \(I\)는 Index set을 의미한다.
점을 변환할때 가장 많이 사용하는 것이 Affine Transformations (아핀 변환) 이다. 아핀 변환은 선형 변환 + 평행 이동까지 포함된 변환이다.
\[A(p) = L(p)+ \vec{t}\]선형 변환은 평행하고, 균등하고, 원점을 보존하는 성질이 있다. 아핀 변환은 평행 이동이 포함되어 있기 때문에 원점을 보존하지 않는다. 대신 평행하고 균등한 성질은 그대로 가진다. 아핀 변환은 아핀 조합을 넣었을 때 다음 성질을 만족해야 한다.
\[A\left( \sum_{i \in I} \lambda_{i} P_{i} \right) = \sum_{i \in I} \lambda_{i}A(P_{i})\]회전과 스케일링은 행렬로 표현할 수 있지만, 평행 이동은 행렬로 표현할 수 없다. 어떻게 해결할까? 차원을 하나 더 늘리면 평행 이동까지 행렬로 표현할 수 있다. 즉, Homogeneous Coordinate를 도입한다.
[!question] 차원 하나를 더 늘리면 평행 이동을 행렬로 표현 가능하다?{title} 예를들어 2차원 벡터를 Homogeneous Coordinate로 표현 후, 행렬을 사용해 평행이동해보자.
\[\begin{pmatrix} 1 & 0 & p \\ 0 & 1 & q \\ 0 & 0 & 1\end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x + p \\ y + q \\ 1 \end{pmatrix}\]
(1) 이동 행렬
\[T = \begin{pmatrix} 1 & 0 & 0 & x \\ 0 & 1 & 0 & y \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \end{pmatrix}\](2) 회전 행렬
\[R_x = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta_x & -\sin\theta_x & 0 \\ 0 & \sin\theta_x & \cos\theta_x & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}\] \[R_y = \begin{pmatrix} \cos\theta_y & 0 & \sin\theta_y & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\theta_y & 0 & \cos\theta_y & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}\] \[R_z = \begin{pmatrix} \cos\theta_z & -\sin\theta_z & 0 & 0 \\ \sin\theta_z & \cos\theta_z & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}\](3) 스케일 행렬
\[S = \begin{pmatrix}s_{x} & 0 & 0 & 0 \\ 0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}\][!example] 원점이 중심이 아닌 오브젝트를 회전하는 예제{title}
\[P' = TRT^{-1}P\]그냥 회전행렬을 적용하면, 오브젝트가 마치 원점을 기준으로 공전하듯 회전하게 된다. 오브젝트를 기준으로 회전하려면 먼저 오브젝트를 원점으로 끌고오고, 회전을 적용한 후 다시 복원해야 한다. 원점에서 오브젝트의 중심으로 이동하는 이동 행렬을 \(T\)라고 가정하면 다음과 같다.
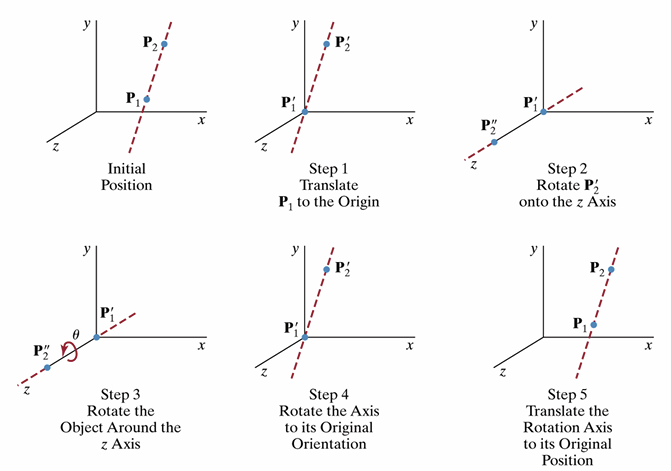
[!example] 임의의 축을 중심으로 회전하는 예제 {title}
축이 원점을 지나지도 않고, 각도도 임의로 주어진 축에 대해 회전하고 싶다.
\[P' = TR_{x}(-\theta_{1})R_{y}(-\theta_{2})R_{z}(\theta)R_{y}(\theta_{2})R_{x}(\theta_{1})T^{-1}P\]
- 축을 지나는 두 점을 알고 있다고 가정한다. 먼저 축을 원점으로 끌고온다. 둘 중 하나의 점으로 변환하는 이동 변환 행렬 \(T\)을 알고 있어야 한다.
- 이후 축을 z축 방향과 동일하게 맞춰야 한다. 이를 위해 x축 기준으로 \(\theta_{1}\)만큼 회전시켜 축을 zx 평면 위에 위치시키고, y축 기준으로 \(\theta_{2}\)만큼 회전시켜 축을 z축과 나란하게 만들 수 있다. 각도는 두 점을 빼면 방향벡터를 얻을 수 있는데, 그 방향벡터와 \(\hat{y}\)을 내적하면 \(\theta_{1}\)를 얻을 수 있고, 회전 후 두 점을 빼서 다시 벡터를 얻은 후 \(\hat{z}\)과 내적하면 \(\theta_{2}\)를 얻을 수 있다.
- 이후 z축 기준으로 회전을 적용한다.
- 2번의 역행렬을 역순으로 적용해 축을 복원한다.
- 1번의 역행렬을 적용해 축을 원래 위치로 복원한다.
이동과 스케일은 크게 문제되진 않는다. 문제는 회전이다! 조금만 상황이 꼬여도 쓰기가 어렵다. 보간도 자연스럽지 않다. 오른쪽 위를 바라보는 애니메이션을 주려 하면 먼저 오른쪽으로 고개를 쭉 돌렸다가 위로 돌리는 부자연스러운 보간이 일어난다.
어디 직관적이면서, 보간도 쉬우면서, 연결도 쉬운 회전 방법이 없을까?
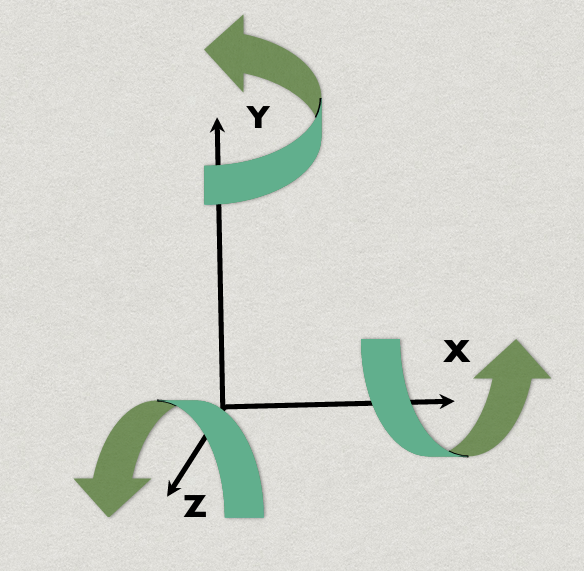
(1) Fixed Angles
위에서 사용한 방법이 Fixed Angles 방법이다. World Coordinate 축 기준으로 회전한다. 위 방식은 간단한 회전도 아주 복잡하게 적용해야 한다. 오브젝트는 그저 자기 기준으로 45도를 돌고싶을 뿐인데 오브젝트의 up벡터를 알아내서 up벡터를 z축으로 맞추고 돌리고 다시 복원해야 하는 개지!랄을 떨어야 한다.
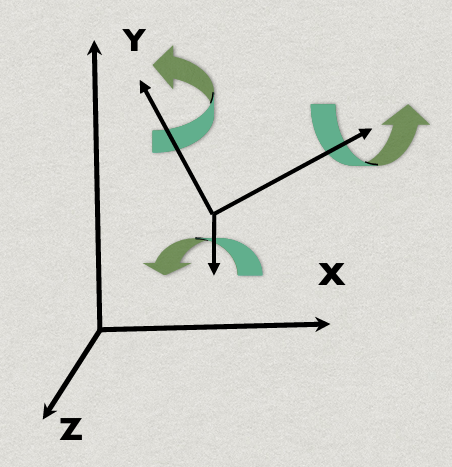
(2) Euler Angles
오브젝트가 기준 축을 가지고 있고, 그 축을 기준으로 회전이 가능하다면 위와 같은 회전이 더 간단해진다. 그냥 본인 기준 up벡터 축을 기준으로 45도 회전하면 된다. 즉, 오일러 각은 본인의 Local Coordinate 축 기준으로 회전한다.
\[(\text{Roll}, \text{Pitch}, \text{Yaw})\]물체는 항상 x축을 바라보고 있다고 가정하고, 물체의 up 방향이 z축의 방향이다. 즉 Roll 각도는 비행기가 방향을 틀 때 기울이는 각도 (갸우뚱 하는 각도), Pitch 각도는 끄덕끄덕하게 하는 각도, Yaw는 좌우로 도리도리하는 각도다.
오일러 각은 Gimbal Lock이라는 심각한 문제가 있다. 만약 Pitch 각도가 \(\pm 90\)이 되어버리는 상황을 생각해보라. 천장 또는 바닥을 수직으로 바라보는 상황이다. 이 경우 비행기가 방향을 틀 때 기울이는 방향과 도리도리하는 방향이 동일해진다. 따라서 회전 축 자유도를 하나 잃는다. 이를 해결하기 위해 다른 회전 시스템을 사용해야 한다.
(3) Axis-Angle 다음과 같은 중요한 정리가 있다.
[!tip] 오일러 회전 정리 (Euler’s Rotation Theorem){title} 3차원 공간 위 Rigidbody를 한 점을 고정시켜놓고 아무리 많은 회전을 수행해도, 결과적으로 단 한번의 회전과 동등하다. 그리고 그 한번의 회전 축은 고정점을 지난다.
Fixed Angle과 Eular Angle에서 보간이 부자연스러운 이유는, 회전이 각각 따로따로 적용되기 때문이다. 위 오일러 회전 정리를 이용해서, 여러 회전을 하나의 회전으로 합쳐버리면 보간이 자연스러워지지 않을까?
\[(\theta, (a_{x}, a_{y}, a_{z}))\]행렬로 표현할 수만 있다면 아핀 변환할 수 있다. 두 행렬 오퍼레이터를 정의하고, 회전 연산을 정의한다.
\[\hat{A} \equiv \begin{pmatrix} a_{x}^2 & a_{x}a_{y} & a_{x}a_{z} \\ a_{y}a_{x} & a_{y}^2 & a_{y}a_{z} \\ a_{z}a_{x} & a_{z}a_{y} & a_{z}^2 \end{pmatrix}\] \[A^* \equiv \begin{pmatrix} 0 & -a_{z} & a_{y} \\ a_{z} & 0 & - a_{x} \\ - a_{y} & a_{x} & 0 \end{pmatrix}\] \[Rot_{(\theta, \vec{a})} = \hat{A} + \cos \theta(I - \hat{A}) + \sin \theta A^*\]이 방법도 단점이 있다. 연속적인 회전 적용이 어렵다. 만약 오브젝트를 연속적으로 회전을 적용한다면, 뒤에 적용하는 회전은 앞에 회전된 결과 효과까지 고려해야 하기 때문이다. 따라서 최선의 방법이 아니다.
(4) Quaternion 쿼터니언이란, 허수부를 3차원으로 확장한 하나의 수다.
\[q = s + x i + y j + zk\]이때 \(i, j, k\)는 각각 다른 방향의 허수 차원이다. 만약 \(z=s + x i\)까지만 있다면 복소수와 같다. 허수는 다음과 같이 정의된다.
\[i^2 = j^2 = k^2 = ijk = -1\]편의상 쿼터니언의 허수 성분을 \(\vec{v}=(x,y,z)\) 벡터로 보고, 다음과 같이 표기한다.
\[q = [s, \vec{v}]\]쿼터니언의 더하기 연산은 다음과 같다.
\[q_{1} + q_{2} = [s_{1} + s_{2}, ~~\vec{v}_{1} +\vec{v}_{2}]\]곱 연산은 다음과 같다. 스칼라부는 스칼라 연산들을 적용하고, 벡터부는 벡터 연산들을 적용한다. 다만 내적했을 때 \(i^2 = j^2 = k^2 = -1\) 성질 때문에, 내적 앞에는 마이너스가 붙는다.
\[q_{1}q_{2} = [s_{1}s_{2} - \vec{v}_{1} \cdot \vec{v}_{2}, ~~s_{1}\vec{v}_{2} + s_{2}\vec{v}_{1} + \vec{v}_{1} \times \vec{v}_{2}]\]내적 연산은 다음과 같다.
\[q_{1} \cdot q_{2} = s_{1}s_{2} + \vec{v}_{1} \cdot \vec{v}_{2}\]내적을 정의했으니 자연스럽게 길이, 단위 쿼터니언도 정의된다.
\[\lvert q \rvert = \sqrt{ q \cdot q }\] \[\hat{q} = \frac{q}{\lvert q \rvert }\]Inverse도 정의된다. \(q q^{-1} = 1\)이 되도록 정의한다.
\[q^{-1} = \frac{1}{\lvert q \rvert^2 }[s, ~-\vec{v}]\]곱셈에 대해 Inverse하면 다음과 같다.
\[(pq)^{-1} = q^{-1}p^{-1}\]뜬금없이 새로운 허수를 왜 정의했냐? 쿼터니언으로 회전을 표현할 수 있기 때문이다!
\[q_{(\theta, ~\vec{A})} = \left[ \cos\left( \frac{\theta}{2} \right), ~\sin\left( \frac{\theta}{2} \right)\vec{A} \right]\]\(\vec{A}\) 축을 기준으로 오른손 방향으로 \(\theta\)만큼 벡터를 회전시키고 싶다면, 위와 같은 쿼터니언을 만든다. 이후 실제 벡터를 회전시키는 연산은 다음과 같다. 먼저 변환할 벡터는 쿼터니언으로 바꿔야 한다.
\[\vec{v} = (v_{1}, v_{2}, v_{3}) \implies v = [0, ~~(v_{1},v_{2},v_{3})]\] \[v' = Rot_{q_{(\theta, ~\vec{A})}}(v) = q v q^{-1}\]위 회전 연산자는 다음과 네가지 성질이 있다.
\[Rot_{q}(v) = Rot_{-q}(v)\] \[Rot_{q}(v) = Rot_{kq}(v)\] \[Rot_{q}(Rot_{p}(v)) = Rot_{qp}(v)\] \[Rot_{q^{-1}}(Rot_{q}(v)) = v\][!note]- 증명{title} 쿼터니언은 덧셈, 곱셈에 대해 결합법칙이 성립한다. 교환 법칙은 덧셈에 대해선 성립하지만, 곱셈에 대해선 성립하지 않는다.
1) \(Rot_{q}(v) = Rot_{-q}(v)\)
\[Rot_{-q}(v) = (-q)v(-q^{-1}) = qvq^{-1} = Rot_{q}(v)\]2) \(Rot_{q}(v) = Rot_{kq}(v)\)
\[Rot_{kq}(v) = (kq)v(kq)^{-1} = \frac{k}{k} qvq^{-1} = Rot_{q}(v)\]3) \(Rot_{q}(Rot_{p}(v)) = Rot_{qp}(v)\)
\[Rot_{q}(Rot_{p}(v)) = q(pvp^{-1})q^{-1} = (qp)v(p^{-1}q^{-1}) = (qp)v(qp)^{-1} = Rot_{qp}(v)\]4) \(Rot_{q^{-1}}(Rot_{q}(v)) = v\)
\[Rot_{q^{-1}}(Rot_{q}(v))=q^{-1}(qvq^{-1})q = (q^{-1}q)v(q^{-1}q) = v\]
\(Rot_{(s, ~(x,y,z))}\) 연산자를 행렬로 변환하면 다음과 같다.
\[R = \begin{pmatrix}1 - 2y^2 - 2z^2 & 2xy - 2sz & 2xz + 2sy \\2xy + 2sz & 1 - 2x^2 - 2z^2 & 2yz - 2sx \\2xz - 2sy & 2yz + 2sx & 1 - 2x^2 - 2y^2\end{pmatrix}\]\(q=[s, ~(x,y,z)]\) 쿼터니언을 보고 \(Rot_{q}\)가 어떤 각도만큼 어떤 축으로 회전할지 알아내는 방법은 다음과 같다.
\[\cos\left( \frac{\theta}{2} \right) = s \implies \theta = 2\cos^{-1}(s)\] \[\vec{v} = (x,y,z)\]쿼터니언은 \(\theta\)를 보간하면 되기 때문에 보간이 쉽다. \(Rot_{q}(Rot_{p}(v)) = Rot_{qp}(v)\) 성질 때문에 연속적인 회전 적용도 쉽다. 짐벌락 현상도 없다. 단점은, 쿼터니언을 보고 이게 어떤 회전일지 바로 연상하기는 어렵다는 것이다. 그래도 쿼터니언이 베스트.