컴퓨터그래픽스 23. Phong Light Model

게시 2025/07/20 업데이트 2025/07/21

By 신희곤

6 분읽는 시간

Phong Lighting Model

빛에서 고려해야할 중요한 요소는 광원과 표면이다. 광원과 표면을 어떻게 모델링 하는지는 반사 모델에 따라 다르다.

광원은 빛의 색상, 위치, 방향, 점광원, 면광원, 감쇠 특성, 빛의 편광 상태 등의 정보를 가질 수 있다.

표면 속성은 표면의 고유 색깔, 위치, 방향, 표면의 미세 구조, 거칠기, 투명도 등의 정보를 가질 수 있다.

퐁 라이팅 모델에서는 광원과 표면 속성을 어떻게 모델링했을까?

광원 = 색상, 위치, 방향, 형태(점, 방향, 면), 감쇠, 편광 특성
표면 속성 = 환경/확산/정반사 반사율, 위치, 방향의 파라미터
카메라 = 위치, 방향, 시야각

위 정보들은 Uniform 변수를 통해 쉐이더로 전달된다고 가정한다.

퐁 라이팅 모델의 아이디어는 다음과 같다.

난반사는 대충 균일하게 퍼지겠지.
정반사는 입사각과 반사각이 같을 수록 많이 보이고, 차이날 수록 적게 보이겠지.
간접 반사 조명 효과는 그냥 전역 조명으로 퉁치자.

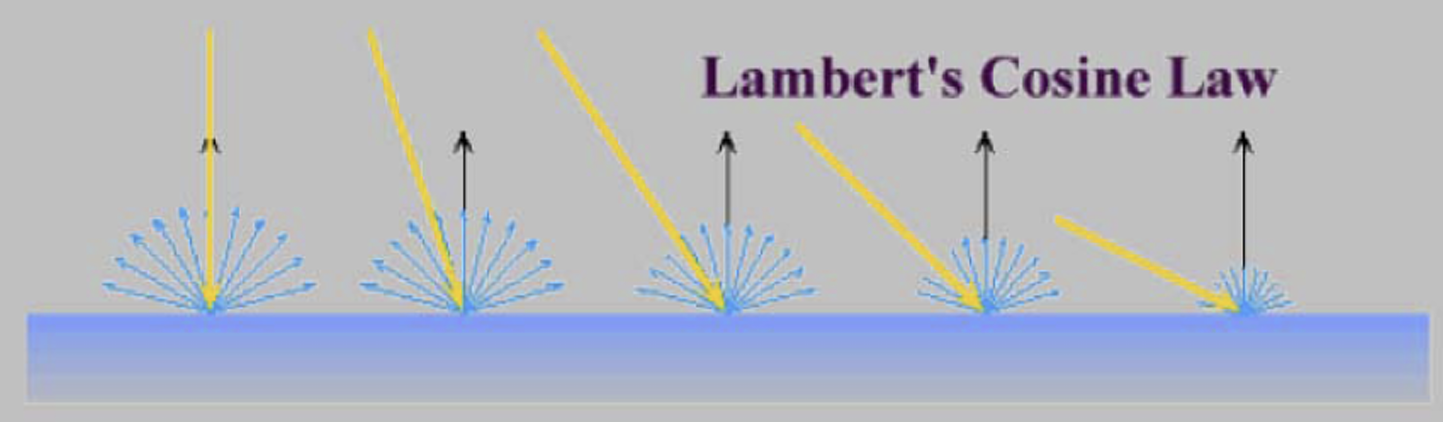
(1) 난반사는 대충 균일하게 퍼지겠지. 이를 람베르트 코사인 법칙(Lambert’s Cosine Law)라고 부른다.

표면과 수직하게 입사할 수록 난반사가 커지고, 비스듬하게 입사할 수록 난반사 양이 작아진다. 즉 난반사되는 빛의 양 \(I_{\text{diffuse}}\)는 표면 벡터와 입사 벡터를 내적한 양과 비례한다. 그리고 비례 상수 \(k_{d}\)를 정의하면 다음과 같다.

\[I_{\text{diffuse}} = k_{d} I_{\text{light}} \hat{n} \cdot \hat{l}\]

\(\vec{n}\)는 표면 법선 벡터, \(\vec{l}\)는 입사광 방향으로의 방향 벡터와 같다. 만약 내적 결과가 음수라면? \(I_{\text{diffuse}} < 0\)이며, 이 경우는 취급하지 않겠다.

(2) 정반사는 입사각과 반사각이 같을 수록 많이 보이고, 차이날 수록 적게 보이겠지.

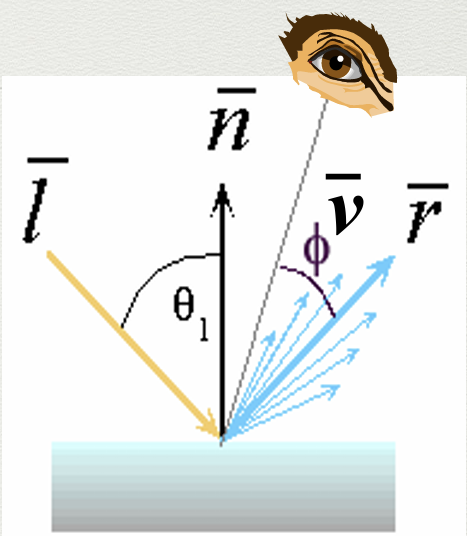
우리의 시선 벡터, 즉 카메라 방향 벡터 \(\hat{v}\)은 Uniform 변수로 주어진다. \(\hat{v}\)와 반사 방향 벡터 \(\hat{r}\)가 일치할 수록 \(I_{\text{specular}}\) 양이 커지며, 그렇지 않을 수록 작아진다. 따라서 비례 상수 \(k_{s}\)와 상수 \(n_{\text{shiny}}\)을 도입하면 다음과 같다.

\[I_{\text{specular}} = k_{s} I_{\text{light}} (\hat{v} \cdot \hat{r})^{n_{\text{shiny}}}\]

\(\hat{r}\)은 어떻게 계산하는가?

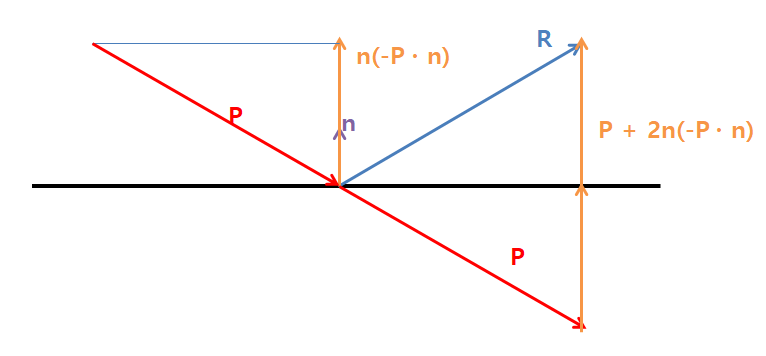
따라서 다음과 같다. 이때 \(P = -\hat{l}\)과 같고, \(\hat{l}\)는 광원 방향으로의 벡터다.

\[\hat{r} = - \hat{l} + 2n(\hat{l} \cdot \hat{n})\]

\(n_{\text{shiny}}\)는 무엇인가? 표면의 광택도와 같다. 이 값이 클 수록 더 집중된 하이라이트가 생기며, 작을 수록 넙대대한 하이라이트가 생긴다.

\(n_{\text{shiny}} = 0.1\): 매우 거친 표면, 넓은 하이라이트
\(n_{\text{shiny}} = 1\): 보통 표면
\(n_{\text{shiny}} = 10\): 매끄러운 표면, 집중된 하이라이트
\(n_{\text{shiny}} > 100\): 거울에 가까운 매우 매끄러운 표면

\(\hat{v} \cdot \hat{r} = \cos \phi \leq 1\)이며, \(n_{\text{shiny}}\) 값이 클 수록 \(\cos \phi\) 항이 빠르게 감소한다. 따라서 시선 벡터가 조금만 벗어나도 하이라이트를 보지 못한다.

(3) 간접 반사 조명 효과는 그냥 전역 조명으로 퉁치자. \(k_{\text{ambient}}\) 상수를 정의하면 다음과 같다.

\[I_{\text{ambient}} = k_{\text{ambient}}I_{\text{light}}\]

왜 이 효과가 필요한가? 없으면 아래처럼 보인다.

있으면 그나마 좀 낫다.

따라서, 최종적인 퐁 셰이딩 모델의 공식은 다음과 같다.

\[I = I_{\text{ambient}} + \sum_{i=1}^{\text{lights}} (I_{\text{diffuse}} + I_{\text{specular}})\]

위는 Ray Casting 식이고, \(\rho(x,x',x'')\)로 표현하면 다음과 같다. 어차피 \(I_{\text{light}}\)는 모든 항에 곱해져 있으므로, 묶어서 따로 분리할 수 있다.

\[\text{lighting}\_\text{model(d,q,l,n)} = \rho(\vec{v}, q, \vec{l}, \hat{n})\] \[= k_{\text{ambient}} + k_{d} \hat{n} \cdot \hat{l} + k_{s}(\hat{v} \cdot \hat{r})^{n_{\text{shiny}}}\]

\(d = \vec{v} = v \hat{v} =\) 시선 벡터
\(q =\) 시선의 위치
\(\vec{l} = l \hat{l} =\) 빛의 입사 방향 벡터의 반대 광원쪽의 방향 벡터
\(n = \hat{n}=\) 표면 법선 벡터
\(\hat{r} = - \hat{l} + 2n(\hat{l} \cdot \hat{n})\) = 반사 벡터

[!NOTE]- 구현 by GPT{title}

  
vec3 phongLighting(vec3 position, vec3 normal, vec3 viewDir, 
                  vec3 lightPos, vec3 lightColor, 
                  vec3 ambient, vec3 diffuse, vec3 specular, 
                  float shininess) {
    vec3 lightDir = normalize(lightPos - position);
    vec3 reflectDir = reflect(-lightDir, normal);
    
    // 환경광
    vec3 ambientColor = ambient * lightColor;
    
    // 확산광
    float diff = max(dot(normal, lightDir), 0.0);
    vec3 diffuseColor = diff * diffuse * lightColor;
    
    // 정반사광
    float spec = pow(max(dot(viewDir, reflectDir), 0.0), shininess);
    vec3 specularColor = spec * specular * lightColor;
    
    return ambientColor + diffuseColor + specularColor;
}

IT, 컴퓨터그래픽스

Phong Lighting Model

인기 태그