컴퓨터그래픽스 22. Rendering Equation

게시 2025/07/20 업데이트 2025/07/21

By 신희곤

14 분읽는 시간

렌더링 방정식이 무엇인가?

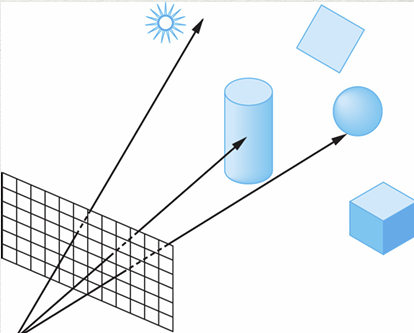
물체는 고유의 색깔이 존재한다. 광원에서 빛이 나와서 물체 표면에 반사 반사되어 우리 눈에 들어온다. 우리 눈에 들어온 빛의 세기에 따라 원뿔세포의 흥분 정도가 결정된다. 즉 빛이 반사되어 카메라로 들어오는 빛의 세기를 계산해야 한다. 그 빛의 세기를 결정짓는 방정식이 렌더링 방정식이다.

\[I(x,x') = g(x,x') \left[ \epsilon(x,x') + \int_{S} \rho(x,x',x'') I(x',x'')dx'' \right]\]

\(I(x,x')\)는 점 \(x'\)에서 \(x\)로 가는 빛의 세기다. \(\epsilon(x,x')\)는 \(x'\)에서 \(x\)로 방출되는 빛의 양이다. 광원일 때 값이 존재한다. \(g(x,x')\)는 감쇠 계수다. \(\rho(x,x',x'')\) \(x''\)에서 온 빛이 \(x'\)에 부딪혀 \(x\)로 갈 때 얼마나 반사되는지 나타내는 반사 계수다.

그래서 렌더링 방정식을 어떻게 써먹는데?

직접 쓰기엔 적분과 재귀식때문에 써먹기 어렵다. 가장 간단하게 2~3번 반사되서 들어오는 빛이 아니라, 광원에서 반사되서 직접 들어오는 빛만 체크해보자. 즉, \(x''\) 위치가 광원일 때만 고려해보자.

\[I(x,x') = g(x,x')\left[ \epsilon(x,x') + \sum_{광원}\rho(x,x',x'')I(x',x'')dx'' \right]\]

이것이 직접 조명 (direct illumination) 방법이다. 이를 쉐이더에서 구현하려면 어떻게 해야할까?

현재 Fragment 위치에서 Ray를 카메라 방향으로 쏜다고 상상하자. 만약 물체와의 교점이 존재하고, 그 물체가 광원이라면 광원 색을 반환한다. 그렇지 않으면 직접 조명광을 계산한다. 교점이 없다면, 배경 색깔을 반환한다.

  
// p = Fragment 위치, d = p - COP 벡터
color trace(point p, vector d)
{
    point q = intersect(p, d, status);
    
    if (status == light_source)
        return light_source_color;
    if (status == no_intersection)
        return background_color;

    n = normal(q); // 교차점 q 표면에서의 노말 벡터
    l = direction(q, light_source_position);
    direct = lighting_model(d, q, l, n);
    
    return direct;
}

\(\rho(x,x',x'') = \text{lighting}\_\text{model}(d,q,l,n)\)
\(\epsilon(x,x') = \text{light}\_\text{source}\_\text{color}\)
\(x = p\)
\(x' = q\)
\(x'' = \text{light}\_\text{source}\_\text{position}\)

위 코드를 Ray Casting이라 한다. 이를 Fragment Shader에서 구현하려면 어떻게 해야할까?

픽셀의 view 또는 world 위치 p는 어떻게 입력받을까?
d는 어떻게 계산할까?
교차점을 어떻게 계산하지?
백그라운드 컬러는 어떻게 알지?
광원 정보들을 어떻게 알지?

(1) 픽셀의 view 또는 world 위치 p는 어떻게 입력받을까? Vertex Processing에서 World Transform 또는 View Transform까지만 적용 후, 그 값을 Fragment Shader로 전달해주면 된다.

(2) d는 어떻게 계산할까? 카메라 위치 COP를 uniform 변수로 전달받으면 된다. 이때 p와 같은 공간에 있어야 한다. World/View Space

(3) 교차점을 어떻게 계산하지? 간단하게 그 픽셀에 해당하는 뎁스 버퍼로 근사한다. 그때 얻는 좌표는 스크린 공간 위의 (픽셀 위치, Depth) 값과 같다. 픽셀 위치는 gl_FragCoord로 얻을 수 있다. 와 같다. 이를 View 또는 World 공간으로 옮겨야 한다.

[!tip] vec4 gl_FragCoord{title}
\[(x,y,z,w)\]
스크린 공간 위의 좌표다. \(x, y =[0,\text{width}] \times [0,\text{height}]\)이다. \(z\)는 깊이값(0.0~1.0)이며, \(w\)는 원근 변환에서 사용한 \(w\)의 역수와 같다. 즉 \(\frac{1}{w}\)다.

따라서 Screen -> NDC -> Clip -> View -> World 공간으로 이동해야 한다.

Screen -> NDC 공간으로 옮기기 위해 vec2 resoultion을 uniform로 입력받는다.

  
// (0.0 ~ 1.0)
vec3 uv = (gl_FragCoord.xy / resolution, depth);

// (-1.0 ~ 1.0)
vec3 ndc = uv * 2.0 - 1.0;

NDC -> Clip 공간으로 옮기기 위해, 원근 나누기의 역을 취한다. 현재 \(\frac{1}{w}\)값을 알고 있다. 따라서, 이 값의 역수를 취해 \(x,y,z\)에 곱해주면 된다.

  
float w = 1.0 / gl_FragCoord.w;

vec4 clipPos = (ndc.xyz * w, w);

View와 World는 역행렬을 uniform 변수로 입력받아, 그저 행렬 벡터곱을 해주면 끝이다.

  
vec4 worldPos = inverseViewProjMatrix * clipPos;
worldPos = worldPos / worldPos.w;

마지막에 w값으로 나눠주는 이유는, \(w=1\)일 때가 아핀 좌표계의 좌표와 같기 때문이다.

(4) 백그라운드 컬러는 어떻게 알지? 유니폼 변수로 하늘 색깔을 주면 된다.

(5) 광원 정보들을 어떻게 알지? World 공간의 광원 정보는 Application State에서 알고 있으므로, unfirom 변수로 전달해주면 된다.

아직 해결하지 못한 질문들은 다음과 같다.

교차점의 물체가 광원인지 아닌지 어떻게 알지?
교차점 표면의 법선 벡터를 어떻게 알지?
라이팅 모델을 어떻게 구현하지?

그러나 위 코드를 그대로 사용하기는 어렵다. 다음과 같은 문제점들이 있기 때문이다.

그림자를 만들지 않는다.
단일 광원인 경우만 고려한다.
- 광원이 여러개라면, 모든 광원에 대해 반복문을 돌려서 최종 색을 혼합해야 한다.
광원에서 표면 사이의 장애물 검사를 하지 않는다.
단일 레이만 고려한다.
- 픽셀당 레이를 여러개를 쏘고 싶은데, 그 방향과 수는 어떻게 결정할까?
재귀적 반사광을 고려하지 않는다.
깊이 버퍼로 교차점을 계산하고 있다.
- 더 정확한 교차점 계산을 해야한다. 이는 고급컴퓨터그래픽스 내용이다.
감쇠 계수를 고려하지 않는다.

앞으로 해결하지 못한 질문들과, 문제점들을 해결해보자.

재귀, 단일, 감쇠계수 문제를 해결하자.

  
color trace(point p, vector d, int step)
{
    if (step > max) return background_color;
    
    point q = intersect(p, d, status);
    if (status == light_source)
        return g(p,q) * light_source_color;
    if (status == no_intersection)
        return background_color;
    
    n = normal(q);
    for (all r, t)
    {
        r = reflect(q,n,d);
        t = refract(q,n,d);
        reflected = lighting_model(d,q,r,n) * trace(q,r,step+1);
        refracted = lighting_model(d,q,t,n) * trace(q,t,step+1);
    }
    
    return g(p,q) * average(reflected + refracted);
}

\(\rho(x,x',x'') = \text{lighting}\_\text{model}(d,q,l,n)\)
\(\epsilon(x,x') = \text{light}\_\text{source}\_\text{color}\)
\(g(x,x') = g(p,q)\)`
\(x = p\)
\(x' = q\)
\(x'' = r, t\)

먼저 재귀를 구현한다. 계산량 폭증을 막기 위해 재귀의 Max 스탭을 제한한다.

그리고 \(g(x,x')\)를 도입한다. 최종 결과에 곱한다.

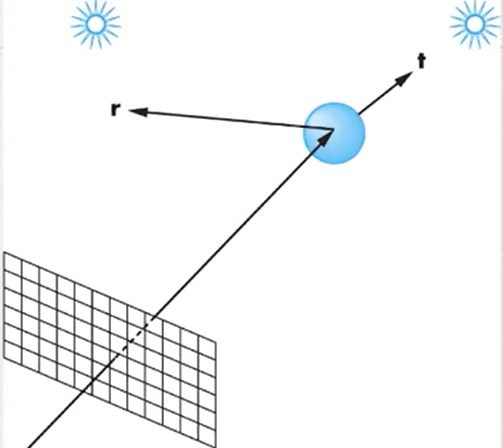
마지막으로, 적분식을 구현한다. 적분식의 의미는, 모든 방향으로 빛이 \(x'\)에 들어오고, \(x\)로 반사되기 때문에 무한대의 방향을 가진다. 그러나 실제로 무한대의 계산은 할 수 없기 때문에, 세가지 방법을 사용한다.

1도씩 Sampling 하거나, 랜덤으로 방향을 정하거나, 미리 정해둔 방향 (Pre-determined shoot)으로만 쏘거나. 방향을 랜덤으로 정하는게 가장 결과가 좋다고 한다. 이 방향을 결정하는 함수를 reflect, refract라고 한다.

[!tip] 교양 지식{title} 랜덤으로 Ray를 쏘거나, 반사 방향을 결정하는 방법을 Monte-Carlo Approach 이라 한다. 레이는 100개부터 많게는 100만개까지도 설정 가능하다.
매 픽셀마다 100만개 레이를 쏘기는 부담스러우므로, 이를 최적화하고자 했다. Radiosity 방법은 정적인 영역(패치)으로 분할하고, 각 패치간의 빛 교환 비율(Form-factor)을 사전에 계산한다. 이는 동적 Scene에 적용하기 어려우며, 메모리 또한 많이 필요하다는 단점이 있다.

이러면 모든 광원의 위치를 알 필요는 없게 되었다. 그러나, 다음과 같은 새로운 물음이 생긴다.

reflect, refract 함수는 어떻게 구현하는가?
g(p,q) 함수는 어떻게 구현하는가?

감쇠 계수 함수는 어떻게 구현하는가?

감쇠 계수 \(g(p,q)\)는 광원의 모델에 따라 다르다. 예를 들어 점 광원은 \(\frac{1}{d^2}\)로 감소할 수 있지만, 그렇지 않은 광원도 있다. 따라서 어떤 라이팅 모델을 사용하냐에 따라서 다른 구현체를 갖는다.

라이팅 모델을 어떻게 구현하지?

라이팅 모델 또는 반사 모델 (\(\rho(x,x',x'')\))은 여러가지 모델이 존재한다.

Blinn-Phong 모델
- 경험적 모델
- 계산이 간단하고, 경험적으로 근사된 반사 모델.
Cook-Torrance 모델
- 물리 기반 모델 (Physically-Based)
- Microfacet 이론을 기반으로 정반사를 현실적으로 구현한 반사 모델.
Oren-Nayar 모델
- 물리 기반 모델 (Physically-Based)
- 거친 람버시안 표면 모델을 기반으로 난반사를 현실적으로 구현한 반사 모델.
Ward 모델
- 경험적/물리 기반 혼합
- Anisotropic (비등방성)으로 인한 하이라이트를 그럴듯하게 표현해준다.
- 비등방성이란, 표면의 결 때문에 빛의 반사가 입사 방향에 따라 달라지는 성질이다.

빛이 표면의 한 점에서 반사 또는 투과되는 모든 현상을 고려한 함수를 일반적으로 BSDF 함수라고 부른다. BSDF는 크게 두가지 함수 BRDF + BTDF로 구분한다.

BRDF는 양방향 반사율 분포 함수로, 반사되는 현상을 다루는 함수다. Blinn-Phong, Cook-Torrance, Oren-Nayar, Ward 모델이 모두 BRDF를 모델링하는 방법이다.

BTDF는 양방향 투과율 분포 함수로, 모든 물체가 불투명하면 고려할 필요가 없다. 유리나, 반투명한 물체가 있을 때 필요하다.

추가적로 BSSRDF 함수는 양방향 표면하 산란 반사율 분포 함수로, 빛이 표면에 들어갔다가 내부 산란 후 다시 다른 점으로 반사되는 현상을 다루는 함수다. 피부, 우유, 왁스 등의 현실적인 구현을 위해 고려되기도 한다.

IT, 컴퓨터그래픽스