컴퓨터그래픽스 15. 컴퓨터에서 색깔을 어떻게 표현할까
색깔은 어떻게 표현할까?
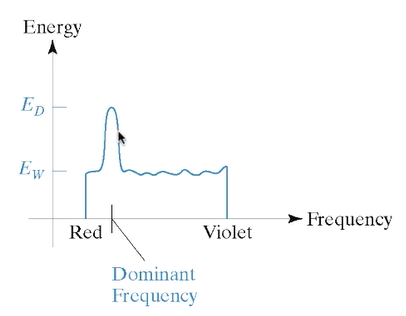
빛은 전자기파면서 광자(Photon)다. 우리는 전자기파 중 특정 파장의 영역만 볼 수 있다. 가시 광선이다. 특정 가시광선 파장을 갖는 단일 전자기파가 우리 눈에 들어오면, 색을 볼 수 있다. 그런데 전자기파는 항상 단일로 존재하진 않는다. 파동이기 때문에, 여러 파장 성분이 중첩되어 있을 수 있다. 여러개의 가시광선으로 중첩되어 있으면, 어떤 색을 보게 될까? 세기가 가장 큰 파장의 색깔을 주로 보게 된다. 빛의 세기란 무엇인가? 빛의 세기는 광자 개수와 비례한다. (광전 효과) 즉, 위치 시간에 대한 빛 신호를 푸리에 변환했을 때 얻는 주파수에 대한 함수값이 가장 큰 주파수 대역 색을 위주로 보게 된다. 그 색의 주파수를 Domiant Frequency 라고 한다.
원뿔 세포의 흥분 정도는 광자 자체의 에너지 \(E=hf\) 에 비례하지 않는다. 예를들어 빨간색과 보라색 파장의 광자가 같은 개수로 들어오면 보라색 위주로 보이는 것이 아니다. 흥분 정도는 광자의 개수와 비례하여 두 색의 균일한 혼합색을 보게 된다.
Hue는 Domiant Color다. Brightness, 밝기는 Total Photon이 결정한다. 즉 들어온 빛의 총 광자 수가 많을 수록 밝다고 느낀다. Saturation, 채도란 색의 순수도다. 빛이 Domiant Frequency로만 이루어질 수록 색은 순수해진다. Domiant Frequency 뿐 아니라 다른 주파수의 색이 섞일 수록 순수한 색에서 멀어지며, 흐릿한 색깔이 만들어진다.
색상 스펙트럼이 연속이면서, 밝기 채도 Hue를 모두 정의 가능한 Color 모델을 어떻게 정의할 수 있을까?
CIE (XYZ) Model이 무엇인가?
목표는 다음과 같다. 색깔 정보를 컴퓨터가 이해할 수 있도록 어떻게 정의할 수 있을까? 모든 색깔을 하나하나 코드로 정의하기엔, 색깔 스펙트럼이 연속적이기 때문에 이론상 무한개의 색깔이 있다. 따라서 불가능하다. 아이디어를 사람의 눈에서 얻는다. 사람의 눈은 특정 몇개의 색깔만을 인식할 수 있다. 그 색깔 비율의 조합으로 색을 인식한다. 즉, 기본 색을 정의하고 그 색을 적당히 혼합하면 모든 색을 표현할 수 있겠네? 그럼 어떤 색을 기본 색으로 정의할까? 깊게 고민할 필요 없이 사람과 같이 Red, Green, Blue를 기본 색으로 정하면 될 것이다.
만약 어디서부터 어디까지가 빨간색 파장이고, 어디서부터 어디까지가 파란색 파장인지 알면 그 파장 값을 경계값으로 설정하고 \((R,G,B)\)로 색을 표현하면 끝나지 않을까? 하지만 애초에 어디서부터 어디까지 빨간색 파장인지 정의할 수가 없다.
따라서 다른 방법을 고안한다. R, G, B 빛을 얼마나 섞어야 특정 색깔을 표현하는지 많은 사람들을 대상으로 무수히 많은 실험을 했다. 그 결과, 다음 세 함수를 만들어내는데 성공한다.
\[\bar{r}(\lambda), ~\bar{g}(\lambda),~ \bar{b}(\lambda)\]함수의 입력은 특정 단색광의 파장이다. 함수의 출력은 필요한 빛의 세기다. 즉 특정 파장 \(\lambda\)의 단색광을 만들려면 빨간색 파란색 초록색 파장의 빛을 얼마나 섞어야 되는지 알 수 있게 되었다. 다만 이 함수는 문제가 있다. 특이 케이스의 \(\lambda\) 값을 넣으면 음수가 생기는 경우가 존재한다. 빨간색 빛을 -20만큼 섞어라? 이게 뭔 개소리야? 따라서, 다루기 편하도록 색깔 함수를 선형변환하여 다른 기저로 표현한다.
\[\begin{pmatrix} \bar{x}(\lambda) \\ \bar{y}(\lambda) \\ \bar{z}(\lambda) \end{pmatrix} = M \begin{pmatrix} \bar{r}(\lambda) \\ \bar{g}(\lambda) \\ \bar{b}(\lambda) \end{pmatrix}\]x, y, z가 다음 특징을 갖도록 정규화한다.
- 항상 0 이상의 값을 가진다.
- \(\bar{y}\)의 크기는 밝기와 동등하다.
[!warning] 이렇게 변환한 x, y, z 값은 각각 r, g, b에 대응되지 않는다. {title} \(\bar{x}\), \(\bar{y}\), \(\bar{z}\)는 \(x=M_{11}\bar{r} + M_{12} \bar{g} + M_{13} \bar{b}\) 와 같이 \(\bar{r}\), \(\bar{g}\), \(\bar{b}\)의 혼합이기 때문이다. 즉 x, y, z는 r, g, b가 아니라, 가상의 (imaginary) 3원색을 의미한다. 가상의 삼원색에서 역 선형변환을 거치면 실제 3원색을 얻는다.
여기까지 하면 단색광 파장 \(\lambda\)의 색은 \(x,y,z\)로 표현할 수 있게 된다. 하지만 여러 파장이 여러 세기로 중첩된 색은 아직 표현할 수 없다. 표현하고 싶은 색의 세기 밀도 \(P(\lambda)\)를 정의하면, 가시광선 파장 범위에 대해 \(P(\lambda)\bar{x}(\lambda)\)를 적분하면 총 필요한 \(x\) 색의 세기를 얻는다. 이를 다음과 같이 정의하자.
\[X \equiv \int P(\lambda)\bar{x}(\lambda)d\lambda\] \[Y\equiv \int P(\lambda)\bar{y}(\lambda)d\lambda\] \[Z\equiv \int P(\lambda)\bar{z}(\lambda)d\lambda\]X, Y, Z를 CIE XYZ 색 공간의 좌표라고 한다. 각각은 imaginary 3원색의 세기와 같다. 실제 빛의 세기 는 Y의 값과 동일하다.
[!warning] Y 값에 대한 오해{title} Y의 크기는 밝기가 맞다. 하지만 그게 색깔이 아니진 않다. Y는 색깔 지표임과 동시에 그 크기가 밝기와 동등한 것이다.
예를 들어, \((X, Y, Z)\) 색에서 밝기를 2배 늘리고 싶다고 Y만 냅다 2배로 올리면 색깔 혼합 비율이 깨져서 다른 색으로 변한다.
\[(X,Y,Z) \neq (X,2Y,Z)\]모두 2배씩 늘려야 동일한 색을 표현하면서 밝기만 2배가 된다.
\[(X,Y,Z) = (2X,2Y,2Z)\]
색깔은 값 자체가 중요하지 않고, 다른 색에 대해 혼합된 비율이 중요하다. 따라서 다음 값을 정의한다.
\[x \equiv \frac{X}{X+Y+Z}\] \[y \equiv \frac{Y}{X+Y+Z}\] \[z = 1-x-y\]이를 xy 색도 좌표라고 한다. 색이 갖는 속성엔 밝기, 채도, 색상(Hue)가 있는데, 그 중 밝기 정보를 뻬고 Hue와 Saturation만 나타낸 좌표다. CIE XYZ 좌표의 총 합을 알면, 색도 좌표에서 CIE XYZ 좌표로 바로 변환할 수 있다.
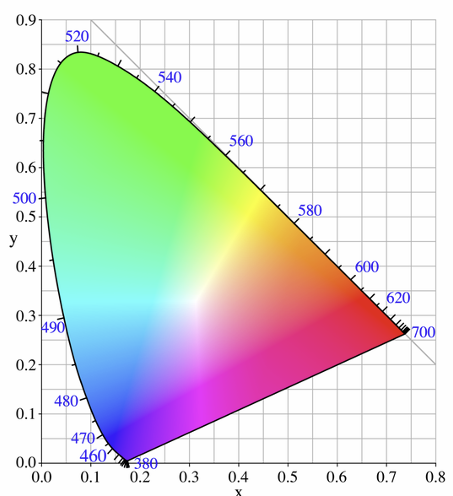
\[X=x(X+Y+Z)\] \[Y=y(X+Y+Z)\] \[Z=(1-x-y)(X+Y+Z)\]x, y를 2차원 평면 그래프로 그리면 아래와 같다.
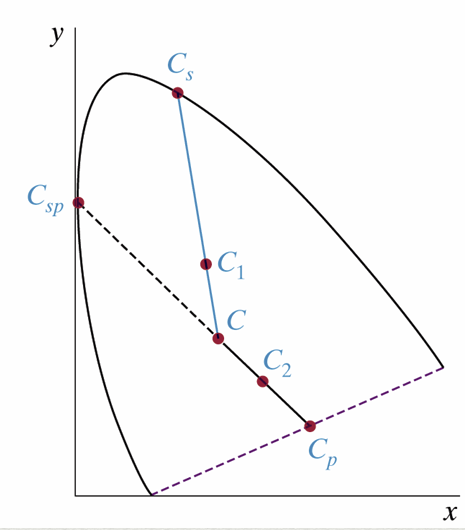
\(C\)는 모든 색이 동일하게 혼합된 Illuminant라고 정의하자. \(C\)와 어떤 색 \(C_{n}\)의 두 점을 직선으로 이었을 때 CIE 그래프와 만나는 지점이 Hue (Domiant Color)와 같다. Saturation가 가장 큰 색은 테두리에 있는 색이다. 안쪽으로 갈 수록 채도가 낮아진다. 밝기는 그냥 Y 값이다.
RGB Model이 무엇인가?
위 모델은 사람이 볼 수 있는 모든 색깔을 다 표현할 수 있다. 하지만.. 모니터는 저 색깔을 전부 표현할 수 없다. 또 사용하기도 불편하다. 따라서 제일 많이 쓰는 모델은 RGB 모델이다.
R, G, B 값을 0에서 1까지 가질 수 있고, 수치를 조절해서 사용한다.
\[(R, G, B)\]순수 색 \(R:(1,0,0),~G:(0,1,0),~B:(0,0,1)\)은 CIE XYZ space에서 어느 좌표인지 정해야 한다. 이 차이가 다양한 RGB 모델 종류가 여러개인 이유이다. sRGB, Adobe RGB, Display P3, Rec. 2020, ... 예를들어 sRGB의 R, G, B 색의 색도 좌표(x, y)는 다음과 같다.
\(R,G,B\) 각각의 \((X+Y+Z)\) 값은 다음과 같다.
\[R\simeq 0.6443, ~~G \simeq 1.192, ~~B \simeq 1.2032\]따라서 \(R, G, B\)의 CIE XYZ 좌표는 다음과 같다.
\[R = (0.4124, 0.2126, 0.0193), ~~G=(0.3576,0.7152,0.1192), ~~B=(0.1805,0.0722,0.9505)\]위 값을 그대로 사용하면 RGB space에서 XYZ space로 변환하는 변환 행렬을 만들 수 있다.\(\begin{pmatrix} X \\ Y\\Z \end{pmatrix} = \begin{pmatrix} 0.4124 & 0.3576 & 0.1805 \\ 0.2126 & 0.7152 & 0.0722 \\ 0.0193 & 0.1192 & 0.9505 \end{pmatrix} \begin{pmatrix} R_{sRGB} \\ G_{sRGB} \\ B_{sRGB} \end{pmatrix}\)
YIQ Model이 무엇인가?
옛날 흑백 티비에서 컬러 티비로 전환되는 과도기에 호환성을 위해 개발한 모델이다. 요즘엔 흑백티비가 사라졌으므로, 안쓴다. 흑백 티비는 밝기 정보만 필요한데, 컬러 티비는 밝기 정보와 색깔 정보가 둘다 필요하다. 이를 동일한 모델로 효율적이게 사용하려면, 밝기 정보와 색깔 정보를 분리할 필요가 있다. 이것이 YIQ 모델이고, 밝기(Y)와 색깔(I, Q) 정보를 다음 공식으로 분리할 수 있다.
\[Y=0.299R + 0.587G + 0.114B\] \[I = 0.5957R - 0.2744G - 0.3213B\] \[Q = 0.2155R - 0.5226G + 0.3111B\]이 모델을 사용하면 흑백티비에는 Y 신호만 주면 되기 때문에 데이터 전송량을 줄일 수 있었다. 위에서 사용한 R, G, B는 sRGB가 아니다. sRGB는 1996년도에 나온 모델이고, YIQ 모델은 1950년대 흑백티비에서 사용할려고 개발된다. 저 RGB 값은 NTSC RGB 표준이고, sRGB와 개념은 같지만 R, G, B의 CIE XYZ 좌표가 다르다.
NTSC RGB 좌표에서 sRGB 좌표로 변환하려면 NSTC RGB 좌표를 XYZ 좌표로 바꾸고, 그 XYZ 좌표를 sRGB 좌표로 바꾸면 된다. 두 변환은 선형 변환이고, 두 변환의 행렬을 곱하면 하나의 행렬로 NSTC RGB -> sRGB로 변환하는 행렬을 만들어낼 수 있다.
CMY, CMYK Model이 무엇인가?
프린터에서 사용하기 위해 개발한 모델이다. 프린터는 빛과 반대로 색을 더할수록 어두워진다. 따라서 RGB를 뒤집은 색깔을 기본 3원색으로 사용한다. 하얀색에서 빨간색을 빼면 청록색 (Cyan), 초록색을 빼면 자홍색 (Magenta), 파란색을 빼면 노란색 (Yellow) 이다. 따라서 CMY 모델이라 부른다.
\[(C,M,Y) = (1,1,1) - (R,G,B)\]단점이 있다. 검은색을 표현하기 위해선 잉크를 세번 칠해야 하고, 낭비로 이어진다. 또 세번 칠하더라도 완전한 검은색으로 보이지 않고 어두운 갈색으로 보이는 좃버그가 있었다. 따라서 검은색 (Key) 을 추가하여 4원색으로 표현하는 모델이 CMYK 모델이다. RGB에서 CMYK로 변환하는 식은 다음과 같다.
\[(C',M',Y') = (1-R, 1-G, 1-B)\] \[K=\text{min}(C', M', Y')\]C’, M’, Y’ 중 최솟값이 K(검정)인 이유는, 이 최솟값이 세 잉크가 가지고 있는 공통 회색성분이고 이를 검은색으로 대체할 수 있기 때문이다.
\(1-K\)로 나누는 이유는 무엇인가? 원래 \(C', M', Y'\)는 0~1 범위를 가지고 있었다. 하지만 \(K\)만큼 뺐으니, 최댓값이 1에서 \(1-K\)로 줄었다. 이를 다시 최댓값 1로 정규화 하기 위해 \(1-K\)로 나눈다.
만약 \(K=1\)이면, 위 식이 정의가 안되므로 예외처리를 해야한다. \(K=1\)이면 검정색만 쓰겠다는 것이다.
\[K=1, ~C=0,~ M=0,~ Y=0\]HSV, HSL 모델이 무엇인가?
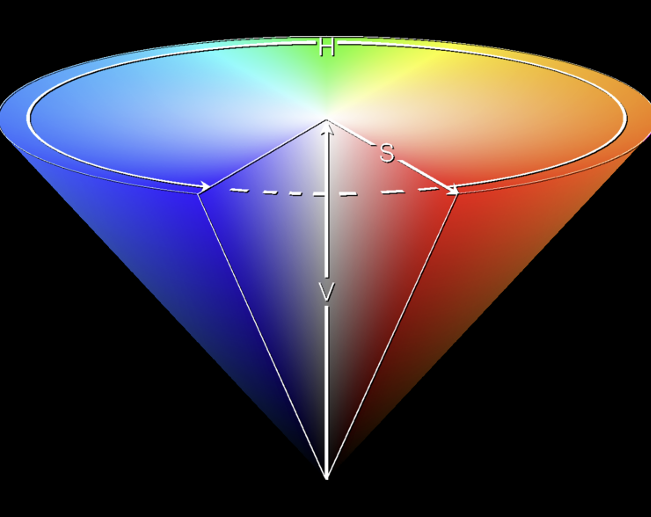
RGB 모델의 단점은 현재 색깔에서 밝기만 줄거나 채도만 줄이거나 하는게 힘들다. 따라서 색의 삼원색을 색상(Hue), 채도(Saturation), 밝기명도(Value) 를 사용하는 모델을 개발한다.
- Hue : 위 space에서 각도와 같다. \(0\degree\)는 빨간색, \(120\degree\)는 초록색, \(240\degree\)는 파랑색이다.
- Saturation : 색의 선명도와 같다. 0% ~ 100% 범위를 가지며 0%에 가까울수록 무채색, 100%에 가까울 수록 쨍한 색깔이 된다.
- Value : 색깔의 밝기와 같다. 0%는 검정색, 100%는 가장 또렷한 색이다.
RGB와 HSV 사이의 변환이 자유자재로 된다면 색깔을 다루는데 아주 편리할 것이다. RGB to HSV 변환 공식은 다음과 같다.
\[\text{Const} = \begin{cases} C_{max} = \text{max}(R,G,B) \\ C_{min}=\text{min}(R,G,B) \\ \Delta = C_{max} - C_{min} \end{cases}\] \[H = \begin{cases} 60\degree \times \left( \frac{G-B}{\Delta}\right) ~\%~ 360\degree & \text{if }C_{max} = R \\ 60\degree \times \left( \frac{B-R}{\Delta} \right) + 120\degree & \text{if }C_{max} = G \\ 60\degree \times \left( \frac{R-G}{\Delta}\right) + 240\degree & \text{if }C_{max} = B \\ \\ 0 \degree & \text{if } \Delta = 0 \end{cases}\] \[S = \begin{cases} 0 & \text{if } C_{max} = 0\\ 1 - \frac{C_{min}}{C_{max}} = \frac{\Delta}{C_{max}} & \text{otherwise} \end{cases}\] \[V = C_{max}\]최댓값을 제외한 나머지 색상을 뺀 후 \(\Delta\)로 나누는 것의 의미가 무엇인가? 우선 \(C_{max}\) 색깔은Determiant Color와 같고, 그 색에서 얼만큼 각도가 틀어졌는지를 나머지 두 색의 차이로 구할 수 있다. 예를 들어 \(C_{max}=G\)면 \(B-R\)을 했을 때 양수값이 나오면 \(B\)쪽에 좀 더 가까운거고, 음수값이 나오면 \(R\) 쪽에 더 가까운 것이다. \(G=120 \degree\), \(R=0\degree\)이므로 음수 방향이 \(R\)이 되도록 설정해야 한다. 같은 원리로 \(C_{max}=G\)의 경우 음수 방향이 \(G\)가 되도록, \(C_{max}=R\)의 경우 음수 방향이 \(B\)가 되도록 설정해야 한다. 이후 \(\Delta\)로 나누면 차이값이 정규화되어 \(-1\)~\(1\) 범위를 갖게 된다. \(60\degree\)를 곱하여 \(-60\degree\)~\(60\degree\) 범위를 갖게하고, 각 색의 Offset 값을 더하면 Hue 값을 얻을 수 있다. Red의 경우 기준이 \(0\degree\)이므로, \(-10\degree\)나 \(380\degree\)와 같이 각도가 범위를 벗어날 수 있다. 그런 각도를 \(0\degree \sim360\degree\)범위로 정규화 하기 위해 나머지 연산을 사용된다. 만약 \(\Delta=0\)이면 최댓값과 최솟값의 색 차이가 없다는 말과 같고, 이는 R G B값이 모두 같은 회색과 같다.
HSV to RGB 변환 공식은 다음과 같다. HSV 값은 H: \(0\degree\)~\(360\degree\), S: 0~1, V: 0~1으로 간주한다.
\[C=V \times S\]Chroma는 위 공식에서 \(\Delta\)에 해당한다. 만약 \(C_{min}=0\)이면 가장 세기가 강한 색의 값은 \(C\)와 동일하다. \(C_{min}\)을 알고있으면, 세기가 가장 강한 색의 값은 \(C+C_{min}\)으로 알 수 있다. 가장 세기가 강한 색의 값은, \(H\)의 범위를 통해 알 수 있다. \(0\degree \leq H < 60\degree\)면 가장 강한 색은 빨간색이고, 두번째로 강한 색은 초록색이다. \(60\degree \leq H < 120\degree\)면 가장 강한 색은 초록색이고, 두번째로 강한 색은 빨간색이다. \(120\degree \leq H < 180\degree\)면 가장 강한 색은 초록색이고, 두번째로 강한 색은 파란색이다. \(180 \degree \leq H < 240\degree\)면 가장 강한 색은 파란색이고, 두번째로 강한 색은 초록색이다. \(240\degree \leq H < 300\degree\)면 가장 강한 색은 파란색이고, 두번째로 강한 색은 빨간색이다. \(300\degree \leq H < 360\degree\)면 가장 강한 색은 빨간색이고, 두번째로 강한 색은 파란색이다.
두번째로 강한 색의 성분은 다음과 같이 계산한다.
\[X=C \times \left( 1 - \left\lvert \left( \frac{H}{60\degree}~\%~2 \right) - 1 \right\rvert \right)\]마지막으로 \(C_{min}\) 값은 다음과 같이 구할 수 있다.
\[C_{min} = C_{max} - \Delta = V - C = V - V \times S = V(1-S)\]최종 \((R,G,B)\) 색은 H의 범위를 분기로 가장 강한 색에 \(C\)값을, 두번째로 강한 색에 \(X\)를 넣고 전체적으로 \(C_{min}\) 값을 구하면 된다. 예를들어, \(120\degree \leq H < 180\degree\)인 경우 가장 강한 색은 초록색이고, 두번째로 강한 색은 파란색이다. 따라서 R, G, B는 다음과 같다.
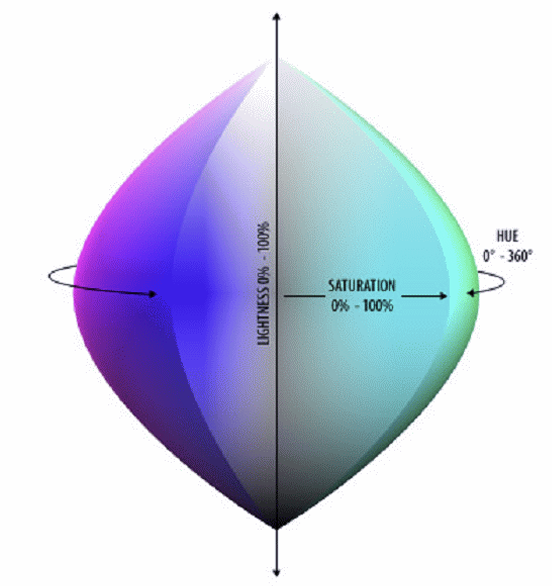
\[(R,G,B) = (C_{min}, ~C+C_{min},~ X+C_{min})\]HSV는 어두운 색의 비율이 많기 때문에, 비율을 맞추고자 Value 대신 Lightness (광도)를 사용하는 모델도 존재한다. L은 0%가 검정이고, 50%가 가장 또렷한 (순수한) 색깔, 100%가 흰색으로 표현된다.
Color Gamut이 무엇인가?
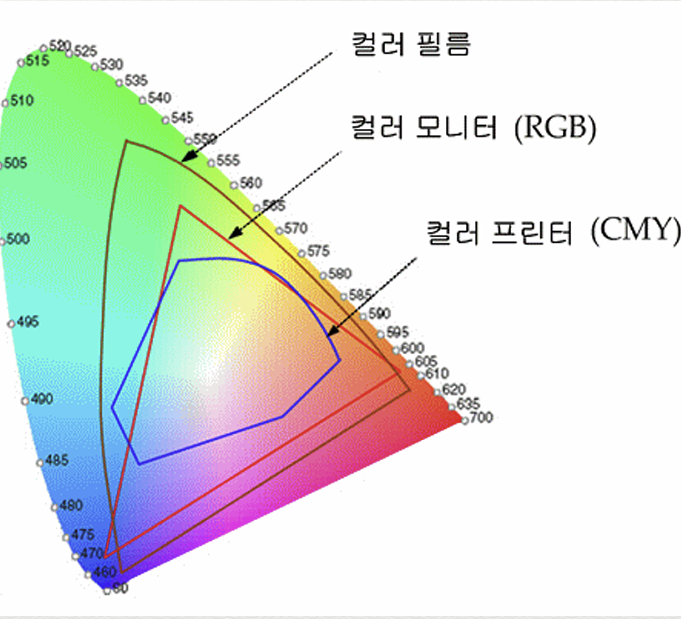
컬러 개멋이란, 표현 가능한 색의 영역을 뜻한다. CIE XYZ space는 이론상 모든 색을 표현하기 때문에, 가장 넓은 Color Gamut을 가진다. sRGB는 그보다 좁은 Gamut을 가진다. xy 색조 영역으로 변환하면 CIE XYZ는 말굽 모양, sRGB는 말굽 모양 내의 삼각형 영역과 같다. Adobe RGB는 sRGB보다 조금 더 넓은 Gamut을 갖는다. CMYK는 sRGB보다 더 좁은 Gamut을 갖는다.
Gamma correction가 무엇인가?
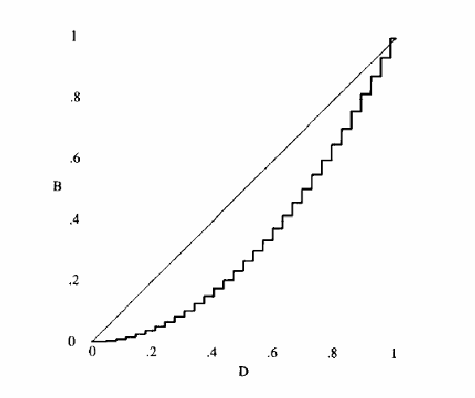
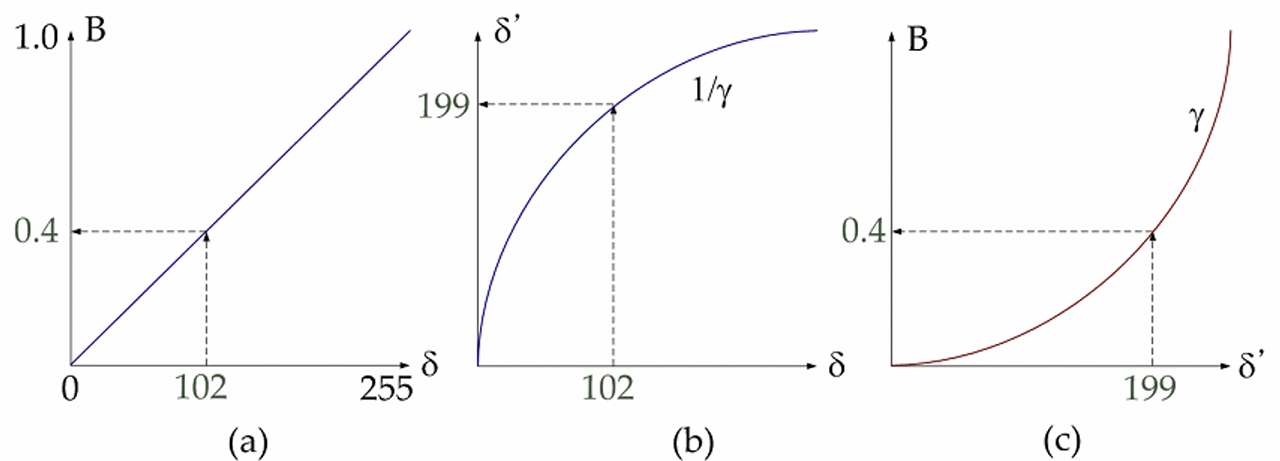
모니터의 빛을 내는 소자에 입력 신호를 넣어주면 빛이 나온다. 입력 신호를 선형적으로 변화시키며 넣어주면, (b)와 같은 결과를 기대했지만 실제로는 어둡다가 갑자기 밝아지는 (a)와 같은 결과가 나온다. 왜 그럴까? 소자에서 빛이 입력 신호에 비례하지 않고, 지수함수 관계에 있기 떄문이다!
입력 신호를 작게주면 계속 어두운 빛만 나오다가, 입력 신호가 커지는 시점에서 급격하게 나오는 빛이 늘어난다. 이를 보정해주는 방법이 Gamma correction이다.
\[B= \alpha \delta^\gamma\]\(B\)는 실제 방출하는 빛의 세기, \(\delta\)는 넣어주는 입력 신호와 같다. \(\alpha\)는 비례 상수, \(\gamma\)도 상수다. \(\alpha\)와 \(\gamma\) 값을 테스트를 통해 찾아내면, 다음 과정을 거쳐 \(B\)와 \(\delta\)를 비례하도록 만들 수 있다.
\[\delta' = \delta^{1/r}\] \[B = \alpha(\delta')^\gamma = \alpha (\delta^{1/\gamma})^\gamma = \alpha \delta\]위 식에서 \(\delta'\)가 실제로 넣어줘야 할 입력 신호와 같다. \(B\)를 알면 \(\delta\)는 간단하게 알 수 있고, \(\gamma\)를 알면 \(\delta\)를 통해 \(\delta'\)를 계산해 실제 넣어줘야 할 입력 신호를 구할 수 있다.
Color Gamut Correction가 무엇인가?
sRGB, Adobe RGB 등 다양한 Gamut을 가진 색 모델들이 있다. 만약 sRGB에서 Adobe RGB로 바꾸고 싶다면, 색깔들을 적당히 보간해서 Adobe RGB의 모든 Gamut을 사용하도록 변환해야 한다. 반대로 Adobe RGB에서 sRGB로 바꾸고 싶다면, 색깔을 잘 꾸겨 넣어서 표현되지 않는 색이 없어야 한다. 이런 문제를 Color Gamut Correction이라고 한다.