컴퓨터그래픽스 14. Rasterization 과정에서 픽셀을 생성하는 방법

Rasterization에서 픽셀을 어떻게 생성하는가?

먼저 Primitive 테두리에 해당하는 픽셀을 구한다. 이후 내부 픽셀들은 Fill Algorithm으로 구하여 프래그먼트를 생성한다.

선분의 시작과 끝 Vertex점의 픽셀 위치를 알고 있다 치면..

선분은 어떻게 그리는가?

방법 (1) 시작 점을 기준으로 주변 점 8개를 \(\varepsilon_{i}\)라고 하자. \(\varepsilon_{i}\)와 목표 점 \(p\)의 맨해튼 거리가 최소가 되는 점을 계속 선택해 나가면 된다. 이 과정은 \(\varepsilon_{i} = p\)가 될 때까지 반복한다.

방법 (2) 두 점을 알고 있으면 직선의 방정식 \(y=mx+n\)의 \(m, n\) 값을 구할 수 있다. 이후 시작 점의 x에서 시작하여 끝점 x까지 x를 1씩 증가하면서 직선의 방정식에 대입하여 y값을 계산한다. 이후 그 y값과 가장 가까운 픽셀을 선택하면 된다.

위 방법은 기울기가 \(0.3\)같이 나오면 매 계산마다 곱셈 나눗셈을 반복하게 된다. 이걸 더하기 빼기만으로 가능하게 할 수 있을까?

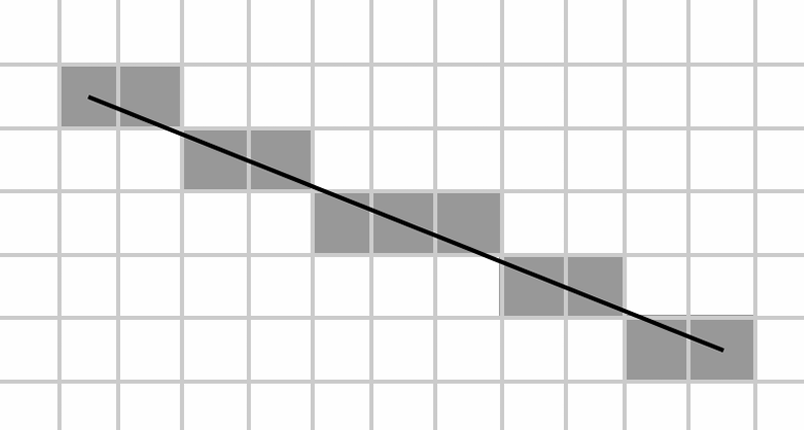
방법 (3) Digital differential analyzer (DDA) \(\Delta x\), \(\Delta y\)를 계산한다. 두 값중 \(\Delta x\)가 더 크면 x 방향으로 1씩 늘리고, \(\Delta y\)가 더 크면 y 방향으로 1씩 늘린다. 이후 step만큼 반복하면서 변분량을 더해가면 된다.

DDA(Point p0, Point p1)
{
    diff = (p1.x - p0.x, p1.y - p0.y);
    step = max(diff.x, diff.y);
    dx = diff.x / step;
    dy = diff.y / step;

    
    for (x = p0.x, y = p0.y, i = 0; i < step; i++)
    {
        plot(x, y);
        x += dx;
        y += dy;
    }
    
    plot(x, y);
}

부동소수점을 사용한다는 단점이 남아 있으므로, 다음과 같은 테크닉을 사용해볼 수 있다.

소숫점 연산을 정수 연산으로 할 수 있는 테크닉. 2/5를 계속 더한다면, 변수 두개를 생성함.

1. numerator
2. denominator numerator를 2씩 더함. denominator를 5로 설정함. numerator가 5보다 커지면 5를 빼서 5보다 작게 만들고, 그때 1을 더함.

이제 선분 그리는 방법으로 Primitive 테두리를 그릴 수 있게 되었다. 그렇다면…

테두리 내부는 어떻게 채우는가?

내부를 채우려면, 어떤 픽셀에 대해서 Primitive 내부에 있는 픽셀인지 외부에 있는 픽셀인지 판별하는 방법이 필요하다. 그 방법은 무엇일까?

방법 (1) Odd-Even Rule (홀짝 규칙) Primitive가 삼각형일때만 사용한다. 현재 픽셀에서 아무 방향으로 Ray를 쏴 봤을 때, 선분과 교차 점이 홀수개면 삼각형 안쪽, 짝수개면 삼각형 바깥쪽임을 알 수 있다. 이를 모든 픽셀에 대해서 수행하면 삼각형에 한에선 모든 Fragment를 찾아낼 수 있다.

방법 (2) Nonzero Winding-Number Rule (감는 수 규칙)

방법 (3) Flood Fill 포토샵이나 그림판에서 물감채우기 할때나 쓰는 알고리즘. 내부 점에서 시작하여 이웃 점이 테두리를 만날 때까지 재귀적으로 반복한다. 이 알고리즘은 레스터화에서 적용하기는 무리가 있다. 그 이유가 무엇인가? 재귀적으로 구현하기 때문에 GPU에서 처리하기 어렵다. 또, 오동작이 발생하는 경우가 존재한다.

방법 (4) Scan-Line Algorithm 하드웨어에서 사용하는 방식이다. 방법은 단순하다. 가로 방향으로 스캔하듯 x축 한 줄에 있는 모든 점을 얻는다. 점을 정렬하고, 점 사이에 있는 픽셀을 모두 프래그먼트로 만들면 된다.

하지만 예외 케이스가 존재한다. 수평선, 꼭지점은 따로 예외처리를 해줘야 한다.

…