컴퓨터그래픽스 12. Primitive를 어떻게 표현할까

Primitive를 어떻게 표현하는가?

(1) 점 : 원점과 벡터로 이루어진다. (2) 직선 직선은 (한 점 + 방향 벡터) or (두 점)이 주어지면 알 수 있다.

\[\vec{P} = \vec{Q} + \alpha \vec{v}\]

두 점이 주어지면, 두 벡터를 빼서 방향 벡터를 만들 수 있다.

\[\vec{P} = \vec{Q} + \alpha (\vec{R} - \vec{Q})\] \[= (1 - \alpha)\vec{Q} + \alpha \vec{R}\] \[= \alpha_{1}\vec{Q} + \alpha_{2}\vec{R}\]

직선은 두 점의 아핀 결합으로 표현될 수 있다. 이때, 계수의 합은 항상 1이다. \(\alpha_{1} + \alpha_{2} = 1\) 아핀 결합 (Affine Combination) 이란, 계수의 합이 1이 되는 선형 결합을 의미한다.

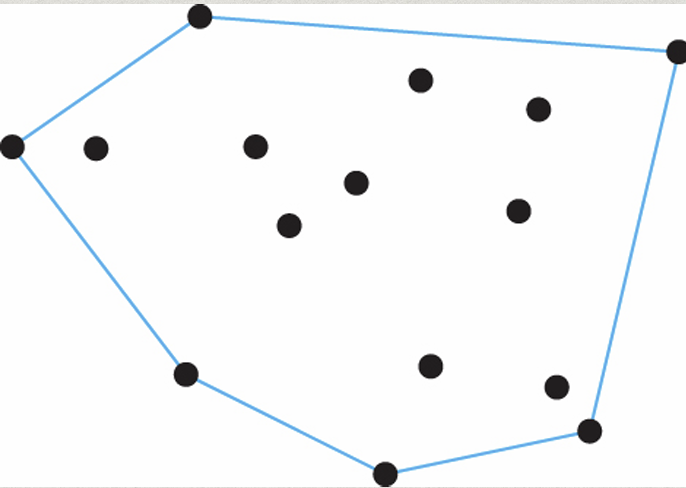
(3) Convex Polygon (볼록 다각형)

Convex Polygon의 내부 영역은 볼록 결합으로 표현 가능하다. (씨발 왜?) 볼록 결합 (Convex Combination) 이란, 계수가 모두 양수인 아핀 결합을 의미한다.

\[\vec{P} = \alpha_{1}\vec{P}_{1} + \alpha_{2} \vec{P}_{2} + \dots + \alpha_{n} \vec{P}_{n}\] \[\sum_{i}\alpha_{i} = 1 ~\cap ~\alpha_{i} \geq 0\]

(4) 평면 세 점이 주어지면 하나의 평면을 결정할 수 있다. 평면 위의 점 \(\vec{T}(\alpha,\beta)\)는 두 방향 벡터 \(\vec{P} - \vec{Q}\), \(\vec{Q} - \vec{R}\)의 선형 결합 (span)으로 표현 가능하다.

\[\vec{T}(\alpha,\beta) = \vec{P} + \alpha(\vec{P} - \vec{Q}) + \beta(\vec{Q} - \vec{R})\] \[\vec{T} = \alpha' \vec{P} + \beta' \vec{Q} + \gamma' \vec{R}\]

평면 또한 세 벡터의 아핀 결합으로 나타낼 수 있다. 만약 볼록 결합이면, \(\vec{T}\)는 평면이 아닌 삼각형을 의미하게 된다.

결론 : Primitive는 일반적으로 Points의 Affine/Convex Combination으로 나타낼 수 있다.