컴퓨터그래픽스 10. Projection
ㅇ
Projection은 어떻게?
투영(사영)이란 무엇인가? 어떤 집합을 부분 집합으로 조건을 만족시키며 옮기는 과정이다. 컴퓨터 그래픽스에선, 카메라가 바라보는 영역 위의 모든 점을 평면 위로 사영하거나, 정규화된 영역 위로 사영한다. 카메라가 보는 시야를 Viewing Volume이라고 부른다. 즉, Vertex를 View Plane 위로 사영하거나, Normalized Viewing Volume 위로 사영한다. 그 과정에서 원근감을 어떻게 살리는지가 관건이다.
먼저 3차원 View Space에서, 2차원으로 투영하는 방법을 살펴보자.
Viewing Volume to View Plane
(1) Orthogonal Projection (직교 투영 모델)
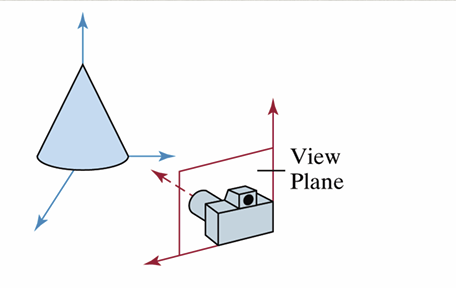
위 그림에서 카메라와 나란하게 View Plane을 이루며, 카메라가 바라보는 방향의 반대 방향이 DOP와 같다. Direction of Projection (DOP)란, Vertex에서 투영되는 방향과 같다. 나중에 보겠지만, 이는 Oblique Parallel Projections의 특수한 케이스와 같다.
카메라는 -z축 방향 \((0,0,-1)\)을 바라본다고 가정한다. 카메라의 위치는 항상 원점 \((0,0,0)\)이며, View Plane은 xy 평면과 같다. DOP는 \((0,0,1)\)이다. 따라서 평면의 방정식은 다음과 같다
\[\hat{n} \cdot (\vec{r} - \vec{r}_{0}) = 0\] \[\implies (0,0,-1) \cdot (\vec{r} - \vec{0}) = 0\] \[\implies (0,0,-1) \cdot (x,y,z) = 0\] \[\implies z = 0\]직선의 방정식은 Vertex를 지나고, DOP 방향과 나란하다. 따라서 다음과 같다.
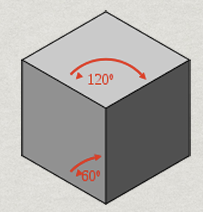
\[(x,y,z) = (v_{x}, v_{y}, v_{z}) + t(0,0,1)\](2) Isometric Projection, Trimetric Projection
위 그림과 같이 정사각형의 윗면이 120도, 옆면이 60도로 보이도록 투영한다. View Transform 단계에서 카메라를 Isometric View 각도로 회전시킨 후, 직교투영하면 된다.
좀 더 자연스럽게 Isometric에서 각도를 좀 더 틀어서 직교투영할 수도 있다. (Trimetric View)
[!tip] 투영 행렬 간단하게 계산하는 테크닉{title} P를 직선 u에 투영하는 투영 행렬, x를 투영시키고 싶은 벡터, u를 투영할 직선의 방향 단위벡터라고 하자. 투영 행렬 P는 \(uu^T\)로 간단히 만들 수 있음을 증명할 수 있다.
\[Px = P(x_{\parallel}+x_{\bot})\]\(x\)를 \(u\)와 평행한 성분과 수직한 성분으로 나눌 수 있다. Let, \(P = uu^T\)
\[= uu^T x_{\parallel} + uu^T x_{\bot}\]이때 \(u^Tx_{\bot} = u \cdot x_{\bot} = 0\)이다. Let, \(x_{\parallel} = ku\)
\[= uu^T(ku)\] \[= k uu^Tu = ku (u \cdot u) = ku = x_{\parallel}\]\(Px\)의 결과가 \(x_{\parallel}\)과 같다. 즉 행렬 \(P\)는 직선 \(u\) 방향에 투영시키는 행렬과 같다.
\[P=\begin{pmatrix} u_{1} \\ u_{2} \\ u_{3} \end{pmatrix} \begin{pmatrix} u_{1} & u_{2} & u_{3} \end{pmatrix} = \begin{pmatrix} u_{1}^2 & u_{1}u_{2} & u_{1}u_{3} \\ u_{2}u_{1} & u_{2}^2 & u_{2}u_{3} \\ u_{3}u_{1} & u_{3}u_{2} & u_{3}^2 \end{pmatrix}\]더 일반적으로, 정규직교벡터 \(u\) set이 만드는 공간 위로 투영하는 행렬 \(P\)은 다음과 같다.
\[P=BB^T, ~~~B=\begin{pmatrix} u_{1} & u_{2} & \dots & u_{n} \end{pmatrix}\]만약 기저 \(u\)가 정규직교벡터가 아니라면, 투영 행렬은 다음과 같다.
\[P=B(B^TB)^{-1}B^T\]예를 들어, 정규직교하는 두 벡터 \(u,v\)는 평면을 Span한다. 이때 그 평면 위로 투영시키는 투영 행렬은 다음과 같다.
\[B = \begin{pmatrix} u_{1} & v_{1} \\ u_{2} & v_{2} \\ u_{3} & v_{3} \end{pmatrix}\] \[P = BB^T = \begin{pmatrix} u_{1} & v_{1} \\ u_{2} & v_{2} \\ u_{3} & v_{3} \end{pmatrix} \begin{pmatrix} u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \end{pmatrix}\] \[= \begin{pmatrix} u_{1}^2 + v_{1}^2 & u_{1}u_{2} + v_{1}v_{2} & u_{1}u_{3} + v_{1}v_{3} \\ u_{2}u_{1} + v_{2}v_{1} & u_{2}^2 + v_{2}^2 & u_{2}u_{3} + v_{2}v_{3} \\ u_{3}u_{1} + v_{3}v_{1} & u_{3}u_{2} + v_{3}v_{2} & u_{3}^2 + v_{3}^2 \end{pmatrix}\]
(3) Oblique Parallel Projection
직교 투영은 너무 정직하게 투영해서 이상해 보인다. 살짝 각도를 줌으로써 좀 더 자연스럽게 만들어보자.
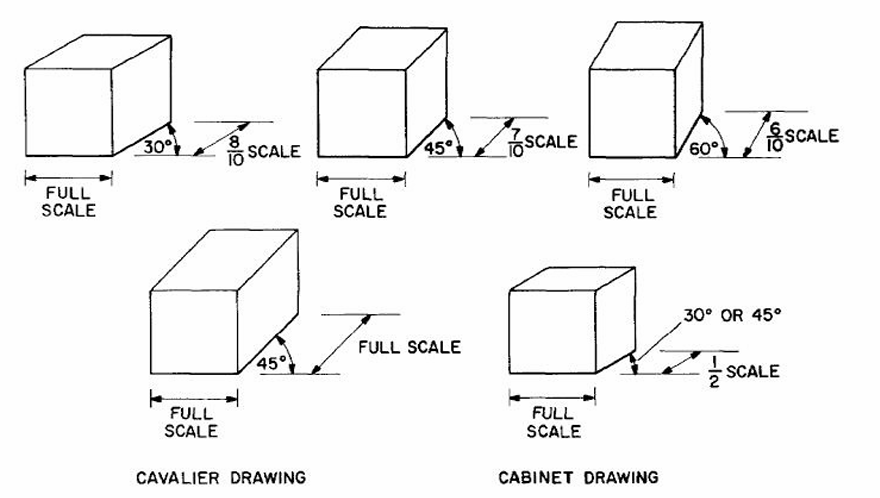
이 방식으로 투영한 결과는 위와 같다. 이번 투영 방식은 가구나 인테리어 디자인에서 많이 사용된다고 한다. 정면은 보존되면서 측면을 입체적으로 보여주기 때문이다.
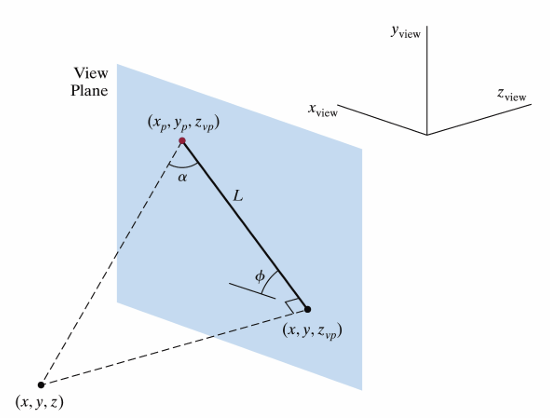
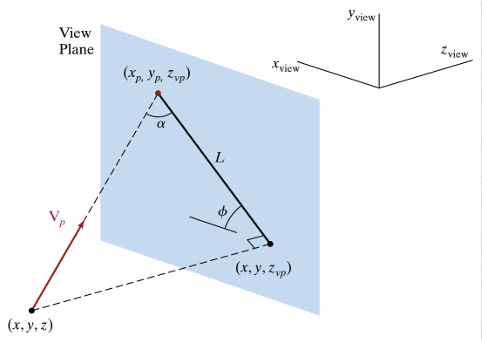
임의의 점 \((x,y,z)\)를 행렬 곱 했을 때 투영된 위치 \((x_{p}, y_{p}, z_{vp})\)가 나오도록 투영 행렬을 구해보자. View Plane은 xy 평면과 나란하고, 그때의 \(z\)값은 고정이므로 \(z \equiv z_{vp}\)로 정의한다.
각도 2개를 파라미터로써 조절할 수 있다. 투영할 점을 \(P\), 투영된 점을 \(P'\), 직교투영한 점을 \(P_{o}\)라고 하자. \(PP'\)와 \(P'P_{o}\) 사이의 각도를 \(\alpha\), \(P'P_{o}\)와 x축이 이루는 각도를 \(\phi\)라고 정의한다. \(\alpha = 90, \phi=0\)이면 직교 투영과 같다. 먼저 \(x_{p}, y_{p}\)는 다음과 같이 간단히 구할 수 있다.
\[\tan \alpha = \frac{z_{vp} - z}{L} \implies L = \frac{z_{vp}-z}{\tan \alpha}\] \[x_{p} = x+L\cos \phi, ~~y_{p} = y+L\sin \phi\]이를 행렬로 나타내면 다음과 같다.
\[\implies x_{p} = x + \left( \frac{z_{vp}-z}{\tan \alpha} \right) \cos \phi= x + 0 + \left( - \frac{\cos \phi}{\tan \alpha} \right)z + z_{vp} \frac{\cos \phi}{\tan \alpha}\] \[\implies y_{p} = y + \left( \frac{z_{vp} - z}{\tan \alpha} \right)\sin \phi = 0 + y + \left( -\frac{\sin \phi}{\tan \alpha} \right) + z_{vp} \frac{\sin \phi}{\tan \alpha}\] \[\begin{pmatrix} x_{p} \\ y_{p} \\ z_{p} \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & - \frac{\cos \phi}{\tan \alpha} & z_{vp} \frac{\cos \phi}{\tan \alpha} \\ 0 & 1 & - \frac{\sin \phi}{\tan \alpha} & z_{vp} \frac{\sin \phi}{\tan \alpha} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}\]\(z=z_{vp}\)로 만들지 않는 이유는, Vertex Processing 이후에 Z-Test와 같은 처리에 깊이 정보가 필요하기 때문이다.
만약 DOP 벡터 \(V_{p}\)가 정의된다면 다음과 같이 쓸 수 있다.
\[\sin \phi = \frac{V_{py}}{V_{px}^2 + V_{py}^2}, ~~\cos \phi = \frac{V_{px}}{V_{px}^2 + V_{py}^2 }, ~~\tan \alpha = \frac{V_{pz}}{V_{px}^2 + V_{py}^2}\] \[P = \begin{pmatrix} 1 & 0 & - \frac{V_{px}}{V_{pz}} & z_{vp} \frac{V_{px}}{V_{pz}} \\ 0 & 1 & - \frac{V_{py}}{V_{pz}} & z_{vp} \frac{V_{py}}{V_{pz}} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]Parameter 값인 \(\alpha, \phi\)를 조절하면 위와 같이 보이게 된다.
(4) Perspective Projection
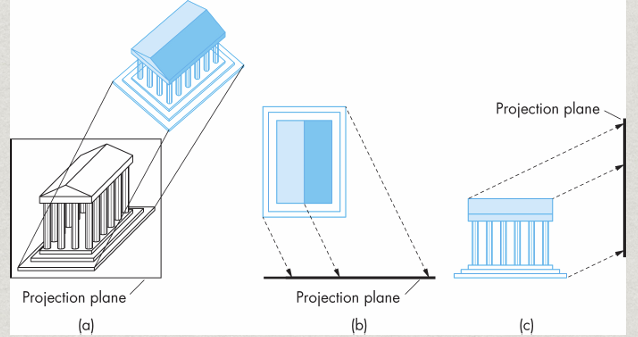
OPP의 문제점은, 위 그림과 같이 현실과 다른 왜곡이 자주 생긴다는 것이다. 왜 왜곡이 생길까? 현실과 다르니까.
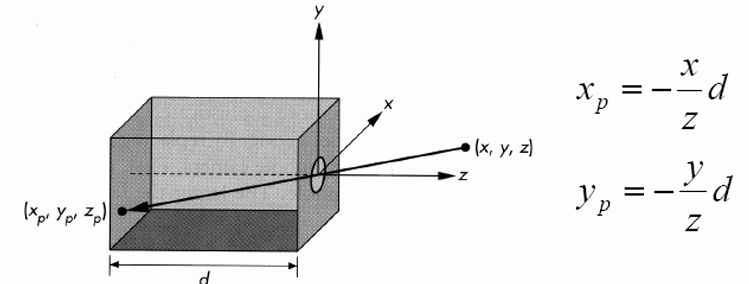
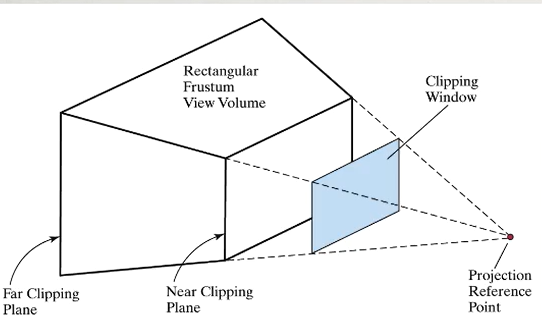
현실에선 빛이 눈, 카메라 렌즈 등의 한 점으로 모이고, 그 점을 지나서 View Plane에 투영된다. 컴퓨터 그래픽스에서 사용되는 원리는 위 그림과 같다. 모든 DOP는 한 점을 지나고, View Plane은 그 앞에 배치하여 투영한다. 이를 Pin hole Camera Model (바늘구멍 카메라)라고 한다.
바늘 구멍의 위치를 COP (Center of Projection)라고 하자. COP 위치는 원점으로 잡는다. Screen Position은 \(z=-d\) 위치로 놓는다. COP와 Vertex Point를 지나는 직선의 방정식은 다음과 같다.
이 직선의 방정식과 \(z'=-d\) 평면의 교점이 투영점이다. 따라서 다음 정보를 얻는다.
\[-d = uz \implies u = - \frac{d}{z}\] \[x_{p} = ux = -\frac{d}{z}x, ~~y_{p} = uy = - \frac{d}{z}y\]이를 행렬로 표현하면 다음과 같다.
\[\begin{pmatrix} x_{p} \\ y_{p} \\ z_{p} \\ 1 \end{pmatrix} = \begin{pmatrix} - \frac{d}{z} & 0 & 0 & 0 \\ 0 & -\frac{d}{z} & 0 & 0 \\ 0 & 0 & 0 & -d \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}\]행렬에 변수 \(z\)가 들어가면 모든 점마다 행렬이 다 다르게 줘야한다. 이러면 Uniform 변수로 주기 곤란하기 때문에, 조작이 필요하다. Homogenous Coordinate위 Point의 \(w\) 성분은 항상 1이다. 따라서 다음 성질이 존재한다.
\[\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} kx \\ ky \\ kz \\ k \end{pmatrix}\]이를 이용하여 행렬을 조작한다.
\[\begin{pmatrix} x_{p} \\ y_{p} \\ z_{p} \\ 1 \end{pmatrix} = \begin{pmatrix} - d & 0 & 0 & 0 \\ 0 & -d & 0 & 0 \\ 0 & 0 & -d & 0 \\ 0 & 0 & 0 & z \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} -dx \\ -dy \\ -dz \\ z \end{pmatrix} = \begin{pmatrix} - \frac{d}{z}x \\ - \frac{d}{z}y \\ - d \\ 1 \end{pmatrix}\]네번째 행을 다음과 같이 바꿔도 동일한 결과를 얻는다.
\[\begin{pmatrix} x_{p} \\ y_{p} \\ z_{p} \\ 1 \end{pmatrix} = \begin{pmatrix} - d & 0 & 0 & 0 \\ 0 & -d & 0 & 0 \\ 0 & 0 & -d & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} -dx \\ -dy \\ -dz \\ z \end{pmatrix} = \begin{pmatrix} - \frac{d}{z}x \\ - \frac{d}{z}y \\ - d \\ 1 \end{pmatrix}\]따라서, 아래 행렬을 핀홀 카메라 투영 행렬로 사용한다.
\[P \equiv \begin{pmatrix} -d & 0 & 0 & 0 \\ 0 & -d & 0 & 0 \\ 0 & 0 & -d & 0 \\ 0 & 0 & 1 & 0 \end{pmatrix}\][!node] Parallel vs Perspective{title} 계산량은 비슷하다. Perspective이 현실적이다. 치수의 정확도를 보존하기 위해선 Parallel을 사용한다.
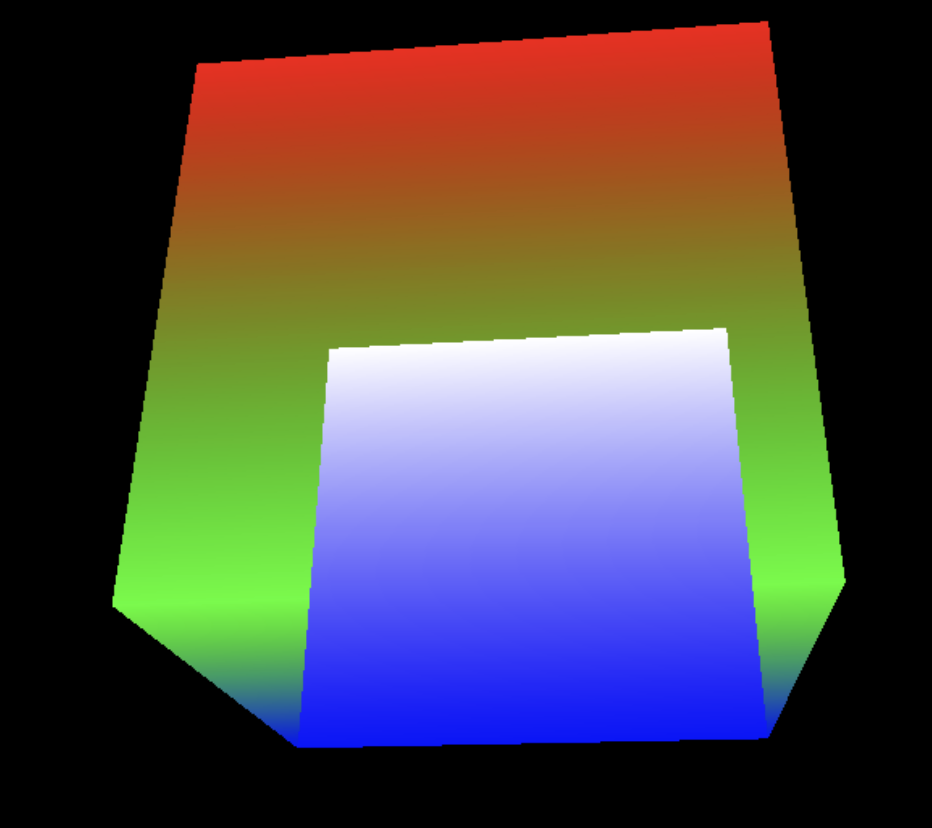
View Plane에 투영하는 방법은, Normalized를 고려하지 않기 때문에 항상 일관적인 화면을 얻을 순 없다. 또, 깊이 값을 날리기 때문에 위 사진과 같이 겹쳐있는 물체를 구분할 수 없다. 따라서 Normalized Viewing Volume에 투영하는 방법이 중요하다.
Viewing Volume to Normalized Viewing Volume
추후 원근 나누기를 했을 때 모든 좌표값이 \((-1, 1)\)가 되어 NDC 공간 내에 들어가도록 정규화해야 한다. 이를 어떻게 할까?
핵심은 다음과 같다. Viewing Volume을 정의하고, 그 Viewing Volume을 정규화하는 변환 행렬을 만드는 것이다.
(1) Orthogonal Projection
직교 투영에서는 \(w\) 성분이 항상 1이다. 따라서 정규화 과정을 거치고 난 뒤의 클립 공간의 좌표 그대로 NDC 좌표가 된다.
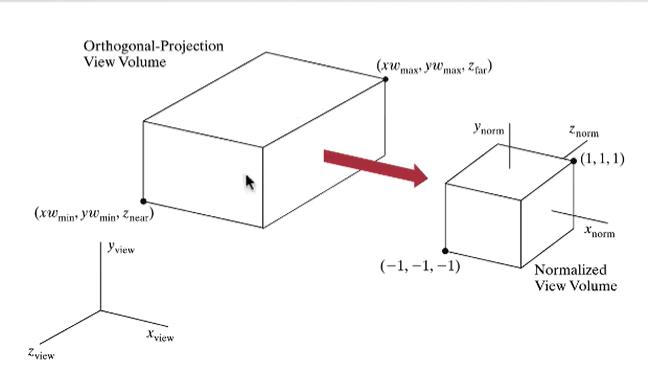
Viewing Volume를 Normalized 하려면, Volume의 폭, 높이, 깊이를 알아야 한다. 깊이 정보 \(z_{near}\)과 \(z_{far}\)는 Camera의 Paramater로 설정한다. 이론상 깊이는 무한이지만, 컴퓨터 연산능력 한계로 인해 제한이 필요하다.
Viewing Volume의 왼쪽 하단 점이 \((x_{min}, y_{min}, z_{near})\)으로 주어지고, 오른쪽 상단 뒤 점이 \((x_{max}, y_{max}, z_{far})\)로 주어지면 다음과 같다.
\[w = x_{max} - x_{min}\] \[h = y_{max} - y_{min}\] \[d = z_{far} - z_{near}\]시야에 보이는 점은 다음 조건을 만족하는 점임을 유의하라.
\[x_{min} \leq x \leq x_{max} ~~\cap~~ y_{min} \leq y \leq y_{max} ~~ \cap ~~ z_{near} \leq z \leq z_{far}\] \[x_{c} = 2\left( \frac{x-x_{min}}{w} \right) - 1 = \frac{2}{w}x - \frac{2x_{min}}{w} - 1\] \[y_{c} = 2\left( \frac{y-y_{min}}{h} \right) - 1 = \frac{2}{h}y - \frac{2y_{min}}{h} - 1\] \[z_{c} = -\left( 2\left( \frac{z-z_{near}}{d} \right) - 1 \right) = - \frac{2}{d}z + \frac{2z_{near}}{d} + 1\]왜 앞에다 2를 곱하는가? \(w\)로 나눠서 정규화하면 0부터 1까지 범위로 주어진다. 실제 범위는 \(-1\)부터 \(1\)까지 이므로 2를 곱해준다. z축의 방향을 뒤집어주기 위해 -를 붙인다. 위 결과를 행렬로 나타내면 다음과 같다.
\[\begin{pmatrix} x_{c} \\ y_{c} \\ z_{c} \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{2}{w} & 0 & 0 & -\frac{2x_{min}}{w}-1 \\ 0 & \frac{2}{h} & 0 & -\frac{2y_{min}}{h}-1 \\ 0 & 0 & - \frac{2}{d} & \frac{2z_{near}}{d}+1 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}\](2) Oblique Parallel Projection
(3) Perspective Projection
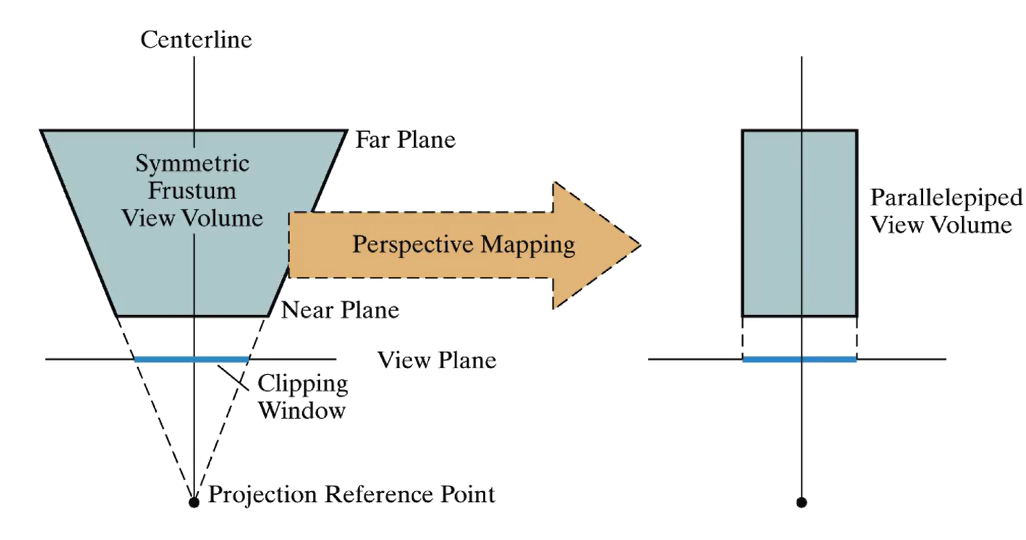
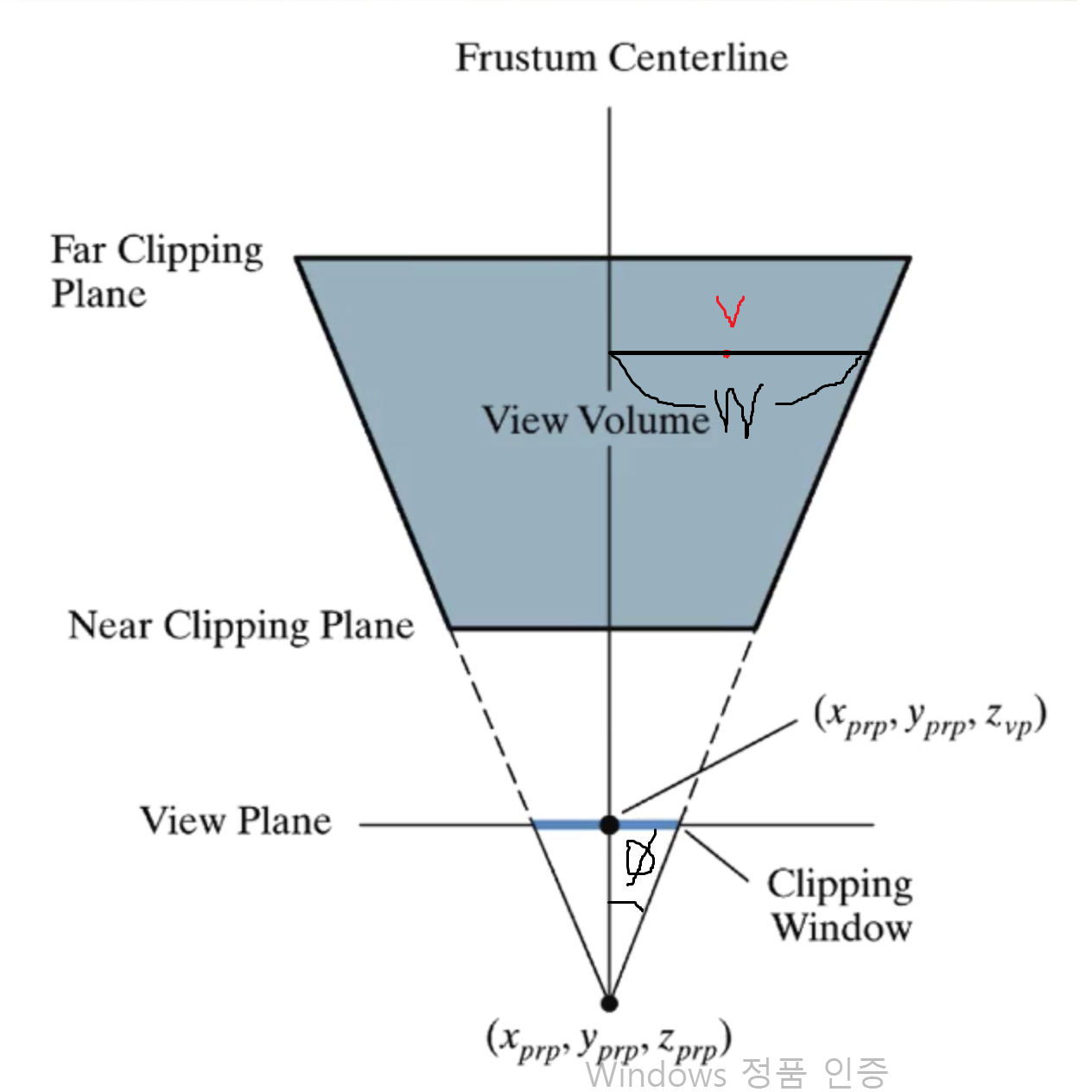
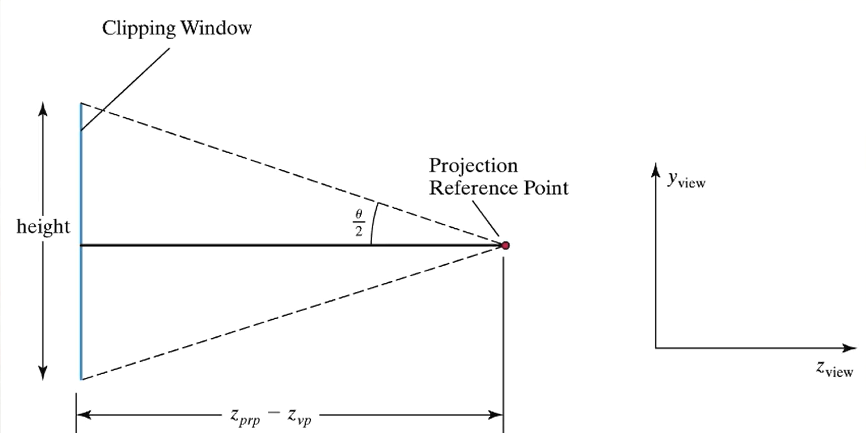
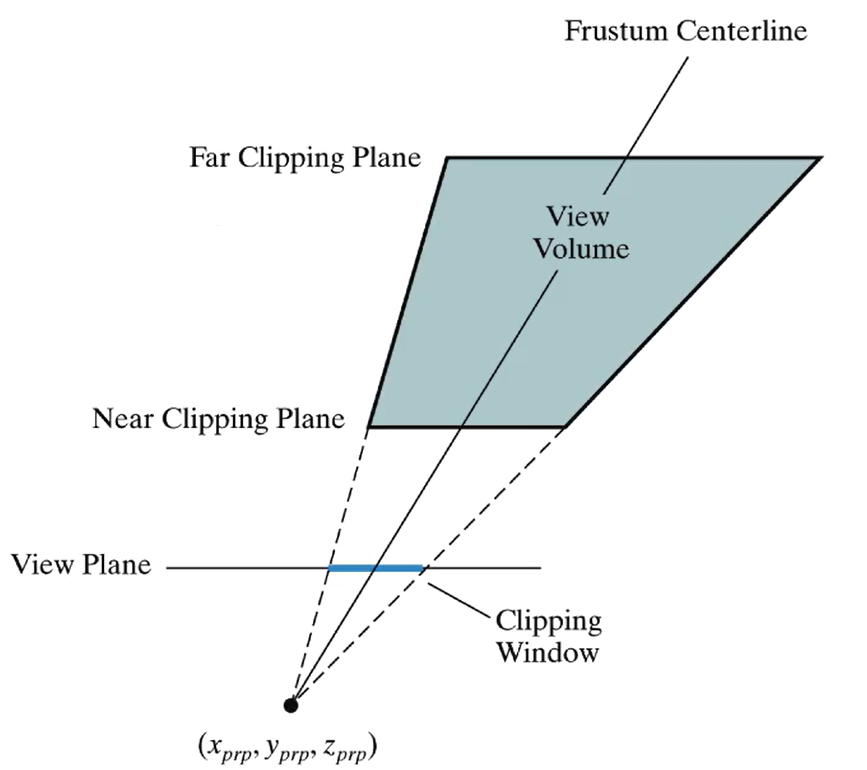
Persepctive에서 Viewing Volume은 Frustum이라고 부른다. Frustum은 피라미드 밑동과 같은 모양이다. Projection Reference Point의 좌표를 일반적으로 \((x_{prp}, y_{prp}, z_{prp})\)로 설정할 수 있겠지만, 그 점을 \((0,0,0)\)라고 잡으면 계산이 간편해진다.
목표는 피라미드 밑기둥 같이 생긴 Frustum을 Normalized Viewing Volume 위로 투영하는 것이다. 따라서 Frustum을 정의한다. Near Plane의 좌측 하단 점을 \((l, b)\), 우측 상단 점을 \((r,t)\), 깊이를 \(n\)이라고 하자. Far Plane의 깊이는 \(f\)으로 하고, 좌측 하단 점과 우측 하단 점은 비례식을 세우면 자동으로 결정된다.
\[n:f=l:l_{f}=r:r_{f}=t:t_{f} : b:b_{f}\]좌측 하단 점은 \(\left( \frac{f}{n}l, \frac{f}{n}b \right)\), 우측 상단 점은 \(\left( \frac{f}{n}r, \frac{f}{n}t \right)\)과 같다.
정규화 핵심 아이디어는, 저 \(W\) 값을 알아낼 수 있으면 정규화 가능하다는 것이다. Vertex의 위치를 \((x,y,z)\)라고 정의 후 구해보자. 최종 목표는\(\frac{(x_{c}, ~y_{c}, ~z_{c})}{w_{c}}\)가 \([-1, 1]\) 범위에 들어오도록 만드는 것이다.
\[\tan \phi = \frac{W}{z} \implies W = z\tan \phi\] \[x_{c} = 2\left( \frac{x-x_{prp}}{W} \right) - 1 = 2\left( \frac{x-x_{prp}}{z\tan \phi} \right) - 1\] \[y_{c} = 2\left( \frac{y-y_{prp}}{H} \right) - 1 = 2\left( \frac{y-y_{prp}}{z\tan \theta} \right) - 1\] \[z_{c} = 2\left( \frac{z-z_{prp}- n}{f-n} \right) - 1\]간단하게 PRP는 \((0,0,0)\)이라고 가정하고, 식을 정리하면 다음과 같다.
\[x_{c} = \frac{2}{z\tan \phi}x - 1\] \[y_{c}=\frac{2}{z\tan \theta}y - 1\] \[z_{c} = \frac{2}{f-n}z - \frac{n}{f-n} - 1\] \[= \frac{2}{f-n}z + \frac{-n - (f-n)}{f-n} = \frac{2}{f-n}z - \frac{f}{f-n}\]행렬로 표현하면 다음과 같다.
\[\begin{pmatrix} x_{c} \\ y_{c} \\ z_{c} \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{2}{z\tan \phi} & 0 & 0 & -1 \\ 0 & \frac{2}{z\tan \theta} & 0 & -1 \\ 0 & 0 & \frac{2}{f-n} & -\frac{f}{f-n} \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}\]현재 행렬에 \(z\) 정보가 들어가 있기 때문에, 동차 좌표계 트릭을 사용해서 행렬에 상수만 남겨야 한다.
\[\begin{pmatrix} x_{c} \\ y_{c} \\ z_{c} \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{2}{\tan \phi} & 0 & -1 & 0 \\ 0 & \frac{2}{\tan \theta} & -1 & 0 \\ 0 & 0 & \frac{2}{f-n}z -\frac{f}{f-n}& 0 \\ 0 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \frac{2}{\tan \phi} - z \\ \frac{2}{\tan \theta} - z \\ \frac{2}{f-n}z^2 - \frac{f}{f-n}z \\ z \end{pmatrix}\]z를 없앨 수 없다. 따라서 \(z_{c}\) 유도할 때 \(z\)를 사용하지 않는 다른 방식으로 구할 필요가 있다.
OpenGL에서 카메라는 \(-z\) 방향을 바라보고, 오브젝트의 \(z\)는 모두 음수값을 가진다. 따라서 축을 뒤집기 위해 \(w_{c}=-z\)로 설정한다.
\(z_{c}\)를 \(-z\)로 나눴을 때, \(z=n\)이면 \(z_{c}=-1\)과 같다. \(z=f\)이면 \(z=1\)과 같다. 즉
\[\frac{z_{c}}{-n} = -1 ~~ \cap ~~ \frac{z_{c}}{-f} = 1\]을 동시에 만족해야 한다.
\[z_{c} = Az + B\]라고 가정하고, 위 방정식에 대입해보자.
\[\frac{An+B}{-n} = -1 \implies An + B = n\] \[\frac{Af + B}{-f} = 1 \implies Af + B = -f\] \[A(n-f) = n+f \implies A = \frac{n+f}{n-f} = - \frac{f+n}{f-n}\] \[\left(- \frac{f+n}{f-n} \right)n + B = n \implies B = n\left( 1+ \frac{f+n}{f-n} \right) = n\left( \frac{f-n +f +n}{f-n} \right) = \frac{2fn}{f-n}\]따라서, \(z_{c}\)는 다음과 같다.
\[z_{c} = \left(- \frac{f+n}{f - n} \right)z + \frac{2fn}{f-n}\]만약 \(\frac{x_{c}}{w_{c}}=\frac{x_{c}}{(-z)}=-1\)이면, 임의의 \(z\)에 대해 \(n:l=z:x\implies x=\frac{l}{n}z\) 관계를 만족한다. 똑같이 \(\frac{x_{c}}{(-z)}=1\)이면, \(n:r=z:x\implies x=\frac{r}{n}z\) 를 만족한다. 따라서
\[x_{c} = Ax+Bz\]라고 가정하고, 연립방정식을 풀어보자.
\[\left( A\left( \frac{l}{n}z \right) + Bz \right) \frac{1}{(-z)} = -1 \implies A\left( \frac{l}{n}\right) + B = 1\] \[\left( A\left( \frac{r}{n}z \right) + Bz \right) \frac{1}{(-z)} = 1 \implies A \left( \frac{r}{n} \right) + B = -1\] \[\implies A\left( \frac{l}{n} - \frac{r}{n} \right) = 2 \implies A = \frac{2n}{l-r} = - \frac{2n}{r-l}\] \[\left( -\frac{2n}{r-l} \right)\left( \frac{l}{n} \right) + B = 1 \implies B = \left(1 + \frac{2l}{r-l} \right) = \frac{r-l+2l}{r-l} = \frac{r+l}{r-l}\]따라서, \(x_{c}\)는 다음과 같다.
\[x_{c} = -\frac{2n}{r-l}x + \frac{r+l}{r-l}\]같은 논리로, \(\frac{y_{c}}{(-z)}=-1\)이면, 임의에 \(z\)에 대해 \(n:b=z:y\implies y=\frac{b}{n}z\) 관계를 만족한다. \(\frac{y_{c}}{(-z)}=1\)이면, \(n:t=z:y \implies y= \frac{t}{n}z\) 관계를 만족한다. 이는 \(l \to b\), \(r \to t\)로 바뀐 대칭 관계이므로 \(y_{c}\)는 다음과 같다.
\[y_{c} = -\frac{2n}{t-b}y + \frac{t+b}{t-b}\]따라서 행렬은 다음과 같다.
\[\begin{pmatrix} x_{c} \\ y_{c} \\ z_{c} \\ 1 \end{pmatrix} = \begin{pmatrix} -\frac{2n}{r-l} & 0 & 0 & \frac{r+l}{r-l} \\ 0 & -\frac{2n}{t-b} & 0 & \frac{t+b}{t-b} \\ 0 & 0 & -\frac{f+n}{f - n} & \frac{2fn}{f-n} \\ 0 & 0 & -1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}\]매개변수를 주는 방법으로 \(r,l,t,b\) 대신 많이 쓰는 방법이 각도를 주는 것이다.
가로 각도와 세로 각도 두개를 줘도 되지만, 일반적으로 많이 사용하는 방법은 아니다. 가장 많이 쓰는 방법은 세로 각도만 주고, Aspect radio 정보로 가로 각도를 계산하는 것이다. 세로 각도를 FOV라고 부른다. FOV와 Aspect radio는 조절 가능한 Camera Parameter와 같다. Aspect Radio는 \(\frac{\text{Width}}{\text{Height}}\)로 계산한다. 그래야 tan(FOV)와 Aspect Radio 값을 곱해야 가로 성분 길이가 계산되기 때문이다.
\[\theta = \text{Height Angle} = FOV\]\(t-b\)는 Near 평면의 Height와 같다.
\[t-b = 2n\tan\left( \frac{\theta}{2} \right)\]\(r-l\)은 Near 평면의 Width와 같고, 만약 가로 각도가 \(\phi\)라면 다음과 같을 것이다.
\[r-l = 2n \tan\left( \frac{\phi}{2} \right) = 2n \cdot Aspect \cdot \tan\left( \frac{\theta}{2} \right)\]Frustum이 대칭이라면, \(r = -l\), \(t = -b\)와 같다. 따라서, \(r+b = r+ (-r) = 0\), \(t+b = t + (-t) + 0\)이다. 최종 투영 행렬은 다음과 같다.
\[P = \begin{pmatrix} -\frac{1}{Aspect \cdot \tan(FOV / 2)} & 0 & 0 & 0 \\ 0 & -\frac{1}{\tan(FOV / 2)} & 0 & 0 \\ 0 & 0 & -\frac{f+n}{f-n} & \frac{2fn}{f-n} \\ 0 & 0 & -1 & 0 \end{pmatrix}\]만약 Frustum이 비대칭이면 어떻게 할까? (Oblique Perspective Projection)
Shearing 되어있는 경우, 역 Shearing 행렬을 적용해서 View Volume을 대칭으로 만들고, Perspective 행렬을 적용하면 된다.
X축 방향으로 Shearing 하는 변환 행렬은 다음과 같다.
\[H_{x}(sh_{xy}, sh_{xz}) = \begin{pmatrix} 1 & sh_{xy} & sh_{xz} & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]\(sh_{xy}\), \(sh_{yz}\)는 각각 xy 평면과 나란한 방향으로, xz 평면과 나란한 방향으로 층밀림 정도를 의미한다.
Y축 방향으로 Shearing 하는 변환 행렬은 다음과 같다.
\[H_{y}(sh_{yz},sh_{yz}) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ sh_{yx} & 1 & sh_{yz} & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]Z축 방향으로 Shearing하는 변환 행렬은 다음과 같다.
\[H_{z}(sh_{zx}, sh_{zy}) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ sh_{zx} & sh_{zy} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]일반적인 Shearing 행렬은 다음과 같다.
\[H = \begin{pmatrix} 1 & sh_{xy} & sh_{xz} & 0 \\ sh_{yz} & 1 & sh_{yz} & 0 \\ sh_{zx} & sh_{zy} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]카메라 효과 구현하는 방법
- Orthogonal Projection
- Pan / Tilt - View Coordinate Rotation
- Crab / Ped - View Coordinate Translation
- Zoom - min/max control
- Track - View Coordinate Traanslation
- Perspective Projection
- Pan / Tilt - View Coordinate Rotation
- Crab / Ped - View Cooridnate Translation
- Zoom - FOV Control
- Track - View Coordinate Translation
Alpha and Blending이 무엇인가?
색깔 정보 R, G, B에 Alpha값을 추가해서 반투명 효과를 계산한다. Alpha and Blending 기능이 켜져있다면, 모드에 따라 겹쳐있는 Fragment의 색깔을 혼합해야 한다. Blending 모드는 다음과 같다.
- Opaque : 덮어쓰기
- Transparent : 알파값대로 섞기
- Additive : 두 색을 더하기
- Multiply : 두 색을 곱하기
그런데 Alpha and Blending 기능을 사용하고 싶은데, Early Z-test를 해버리면 뒤에 겹쳐있는 프레그먼트가 다 걸러지니까 문제가 되는거 아닌가? 맞다! 그래서 Alpha값을 통해 혼합 모드를 키면 자동으로 Early Z-Test 기능이 꺼진다. 따로 신경써줘도 좋다.