포스트

인공지능 9. 결정론적 지식을 다루는 방법

게시
By 신희곤
16 분읽는 시간
인공지능 9. 결정론적 지식을 다루는 방법

결정론적 지식을 어떻게 모델링할까?

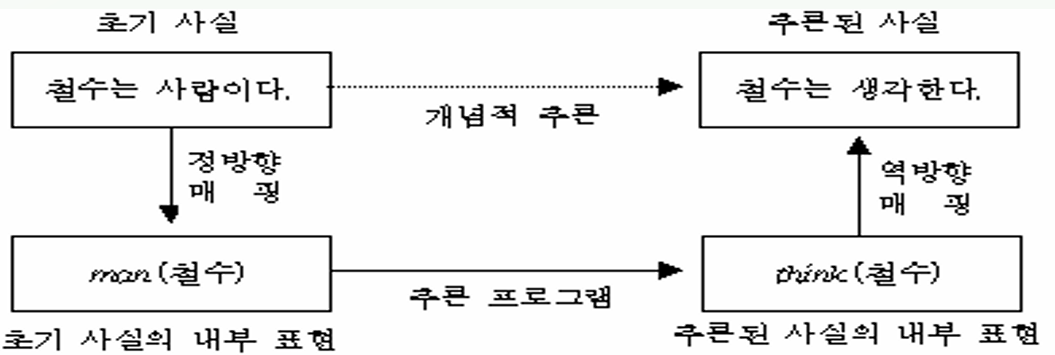
가장 기본적인 아이디어는, 우선 인간이 이해 가능한 사실을 기계가 이해 가능한 사실로 매핑해야 한다. 이후 기계가 추론 과정을 통해 새로운 지식을 출력하고, 그 출력한 지식을 다시 인간이 이해 가능한 사실로 역매핑하는 과정을 거친다.

Pasted image 20250614132603.png

사실을 기계가 이해 가능하도록 표현하는 방법에는 네가지가 있다.

(1) 규칙 기반 시스템(Rule-Based Systems) 해당 시스템에는 규칙과 사실이 존재한다. 규칙이란 만약 \(P\)이면, \(Q\)이다. 즉 \(P \to Q\) 관계가 하나의 규칙이다. 이때 \(P\), \(Q\)가 하나의 사실이다. 사실은 컴퓨터가 이해하지 못하고 그냥 문장 형식으로 저장된다. 따라서 지식이란 (사실 + 규칙) 이다.

예를들어, 규칙 리스트 \(\{R_{1}, R_{2}, \dots, R_{n}\}\)이 있을 때 초기 사실 \(\{F_{1}, F_{2}, \dots \}\)에서 시작하여 도달할 수 있는 모든 사실관계를 얻어내는 것을 순방향 추론 (Forward Chaining) 이라 한다. 액체 pH=3 → 산 판정 → 초산 결론

반대로, 얻고 싶은 사실 \(F\)에서 시작하여 필요한 조건들을 역추적해서 구할 수 있다. 이를 역방향 추론 (Backward Chaining) 이라 한다. 역방향 추론은 어떤 가설을 증명할 때 사용할 수 있다. 또는 어떤 사실을 만들어내기 위해서 어떤 조건들이 필요한지 구하고 싶을 때도 사용 가능하다. 초산인가? → 산인가? ∧ 냄새=식초인가? 확인

위 방법은 규칙을 사람이 일일히 지정해줘야 하는 불편함이 있고, 사실 자체는 컴퓨터가 이해하지 못하므로 체계적이지 못하다는 느낌을 받는다.

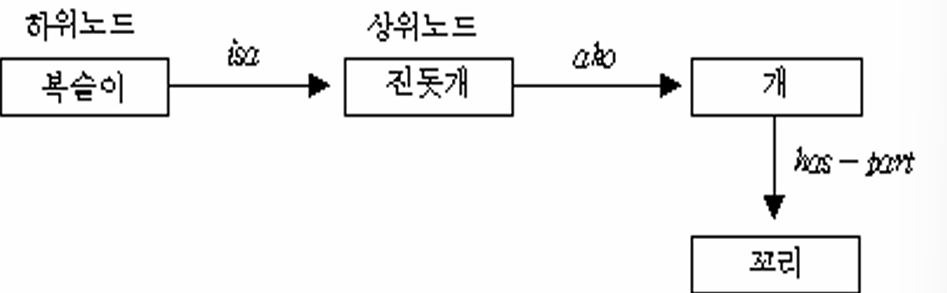
(2) 의미망(Semantic Net) 의미망은 위 규칙기반 시스템을 확장한 것이다. 객체를 노드로, 객체 사이를 연결하는 관계를 단방향 엣지로 나타낸다. 이 엣지를 아크라고 한다. 객체 사이의 관계는 다음과 같다.

  • is a (isa): 상속 관계. 하나의 사례. ako보단 더 구체적이다.
  • a kind of (ako): 상속 관계. 하나의 종류. isa보다 더 추상적인 관계다.
  • has-part: 부품 관계.

[!example] 예시{title}

  • 진돗개는 개의 한 종류이다. = ako(진돗개, 개)
  • 개는 꼬리가 있다. = has-part(개, 꼬리)
  • 복슬이는 진돗개이다. = isa(복슬이, 진돗개)

Pasted image 20250614135906.png

어떤 객체 \(O\)의 속성 \(A\)가 있는지 찾아내는 알고리즘을 특성 상속 알고리즘이라고 한다. 아이디어는 간단하다. 먼저 객체 \(O\)가 직접 \(A\)를 갖고있는지 체크한다. 갖고있지 않으면, 상속 관계인 부모로 이동해서 그 부모가 \(A\)를 갖고있는지 체크한다. 갖고있다면, \(O\)는 \(A\)를 갖고 있다고 판단하고 종료한다.

이때 상속 관계는 isa, ako 관계와 같다. 이게 가능한 이유는 무엇인가? 부모, 즉 추상 객체가 가지고 있는 모든 속성은 하위 구현 객체가 상속받기 때문이다.

(3) 프레임(Frame) 의미망을 쓰다보니깐.. 뭔가 상속 개념이 객체지향이랑 비슷한데? 그럼 객체처럼 만들어 볼까? 이것이 프레임이다.

객체가 프레임이고, 프로퍼티는 슬롯이고, 프로퍼티의 값은 슬롯의 값과 같다. 메서드는 프로시저(Procedure)라고 한다.

예를들어, 복슬이의 속성 중 isa으로 진돗개를 가지고 있고, ako에 개, 포요류 등을 가지고 있다. 추가 슬롯으로 다리 개수, 털 색깔 정보도 담을 수 있다.

프로시저는 프레임에 미리 정의된 동작이다. 어떤 이벤트가 발생하면, 프로시저가 실행되어 지식을 자동으로 관리하도록 만든다. 프로시저 종류는 다음과 같다.

|프로시저 종류|실행 시점 (Trigger)|주된 목적| |—|—|—| |When-Needed|값이 필요한데 비어있을 때|값의 동적 계산, 외부 조회| |When-Read|값이 읽힐 때마다|접근 기록, 데이터 포맷팅| |When-Written|값이 쓰여지거나 변경될 때|연관 데이터 업데이트, 유효성 검사| |When-Removed|값이 삭제될 때|연관 데이터 정리, 관계 해제| 예를들어 사각형 프레임이 가로, 세로, 넓이 슬롯을 가지고 있다고 하자. 넓이 슬롯의 값은 가로 또는 세로의 값이 변경될 때, 즉 When-Written일 때 업데이트되면 된다. 이런 식으로 프로시저를 활용한다.

이렇듯 지식을 프레임으로 관리할 수도 있다.

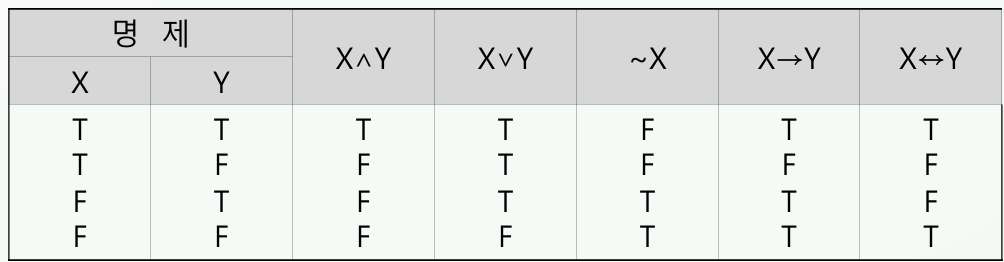
(4) 명제 논리(Propositional Logic) 명제가 무엇인가? 명제란, 참/거짓 판단이 가능한 문장이다. 명제들을 논리 연산자로 연결한다. 논리 연산자는 다음과 같다.

\[\land = \text{AND}, ~~\lor = \text{OR}, ~~\lnot = \text{NOT}, ~~\to = \text{조건}, ~~ \leftrightarrow = \text{동치}\]

Pasted image 20250614151139.png

각 명제를 하나의 심볼 (\(P, Q, X, Y, \dots\))로 표현한다. 이 심볼들을 논리 연산자로 연결한 것을 복합명제라고 한다.

즉, 명제는 사실이며 지식은 명제 또는 복합명제와 같다.

이제 논리학에서 증명된 것들을 끌어와서 추론 과정에 사용할 수 있게 되었다. 논리학에서 사용되는 것들은 다음과 같다.

[!NOTE] \(A\)가 거짓이면, 명제 \(A \to B\)는 반드시 참이다.{title} 예를들어, ‘달이 네모라면 나는 날 수 있다.’는 반드시 참이다. 뭔 뚱딴지 같은 소리냐? 애초에 달이 네모라는 가정이 거짓이기 때문에, 논리적으로 참인 것이다. 그 이유는 다음 관계가 성립하기 때문이다.

\[A \to B = (\lnot A) \lor B\]

\(A\)면 \(B\)이다가 참인 것은, \(\lnot A\)가 참이거나 \(B\)가 참이면 된다. 왜? \(A \to B\)가 거짓이 될 때는 \(A\)가 참이면서 \(B\)가 거짓일 때 뿐이기 때문이다.

\[A \to B = \lnot( A \land \lnot B ) = (\lnot A) \lor B\]

또는, 집합론으로 증명도 가능하다. 어떤 명제 \(P\)는 명제 \(P\)를 참으로 만드는 모든 경우의 집합 \(Set(P)\)와 같다.

\[P \leftrightarrow Set(P)\]

즉, \(A\)이면 \(B\)이다 관계는 \(Set(A)\)가 \(Set(B)\)의 부분집합인 것과 같다. 아래 관계는 동치 관계이다.

\[A \to B \leftrightarrow Set(A) \subseteq Set(B)\]

이때 \(A\)가 항상 거짓이면? \(Set(A)\)는 공집합이다. 그리고 공집합은 모든 집합의 부분 집합이다. 따라서 \(Set(A) \subseteq Set(B)\)가 항상 성립된다. 따라서 \(A\to B\)가 항상 성립된다.

[!NOTE] Modus Pones (가언적 삼단논법){title}

\[P \to Q\]

인 사실을 알고 있다. 이때 \(P\)라는 사실이 주어지면, \(Q\) 또한 사실이라는 것을 추론할 수 있다. 주의할 점은, \(\lnot P\)라면 \(\lnot Q\)인 것은 아니다. 예를들어, 비가 오면 -> 땅이 젖는다. 만약 비가 왔다면, 땅이 젖을 것이다. 그러나 비가 오지 않으면, 땅이 안젖는건 아니다.

[!NOTE] Modus Tollens (부정 논법){title} 가언적 삼단논법에서, 대우를 취한 결과도 새로운 사실이다. 즉

\[P \to Q\]

라면, 대우를 취한

\[\lnot Q \to \lnot P\]

것도 사실이다.

예를들어 비가 오면 -> 땅이 젖는다. 땅이 젖지 않으면 -> 비가 오지 않는 것이다. 이것은 사실이다.

[!NOTE] 삼단논법{title} 나는 \(A \to B\)라는 사실을 알고 있다. 이때 \(B \to C\)라는 새로운 사실이 주어지면, \(A \to C\) 또한 사실이다.

예를들어 소크라테스 -> 인간, 인간 -> 언젠가 사망이면 소크라테스 -> 언젠가 사망은 사실이다.

[!tip]- 추가적으로 논리학에서 사용될 수 있는 추론 규칙…{title}

  • AND elimination
  • Double negation elimination
  • Implication elimination
  • Biconditional elimination
  • De Morgan’s Law
  • Distributive Law
  • Complementary literal
  • Advanced complementary literal

그래서 명제 논리로 추론을 어떻게 할까? 먼저 사실을 CNF로 변환한다. CNF로 변환하면, 위반 규칙을 사용해서 새로운 사실을 추론할 수 있다.

Conjunctive Normal Form (CNF) 식은 AND로 연결되어 있는 하나의 식이다. 모든 사실은 CNF 식으로 변환할 수 있다.

  1. \(\leftrightarrow\)를 제거한다. \(A \leftrightarrow B \equiv (A \to B) \land (B \to A)\)
  2. \(\to\)를 제거한다. \(A \to B \equiv \lnot A \lor B\)
  3. \(\lnot\)를 드모르간으로 분배한다. \(\lnot(A \land B) = \lnot A \lor \lnot B\)
  4. 괄호 안에 AND가 있으면, 분배한다.
    • \(A \lor (B \land C) = (A \lor B) \land (A \lor C)\)

위반 규칙이란, 두개의 절 \((P \lor A)\)와 \((\lnot P \lor B)\) 둘다 참이라는 사실을 알고 있다고 하자. 즉 다음 CNF 식이 참이다.

\[(P \lor A) \land(\lnot P \lor B)\]

\(P\)가 참이면, \(B\)가 참이어야 한다. 반대로 \(P\)가 거짓이면, \(A\)가 참이어야 한다. \(P\)는 반드시 참 또는 거짓이므로, \(A\) 또는 \(B\)는 반드시 참이다. 따라서 다음 새로운 사실을 추론할 수 있다.

\[A \lor B\]

(5) 술어 논리(Predicate Logic) 명제 자체는 규칙 기반 시스템과 같이 컴퓨터가 이해할 수 없다는 단점이 있다. 따라서, 명제 내부의 객체들을 추출하고, 그 명제들의 관계를 나타내는 방법이다. 그 관계는 술어 (Predicates) 기호로 나타낸다. \(\forall, \exists\)와 같은 한정사 (Quantifiers) 를 사용할 있다.

예를들어 소크라테스는 사람이다. 모든 사람은 죽는다. 따라서 소크라테스는 죽는다를 술어로 표현하면 다음과 같다.

\[\text{Human}(\text{소크라테스}), ~~ \forall x ~~ \text{Human}(x) \to \text{Mortal}(x)\] \[\therefore ~~ \text{Mortal}(\text{소크라테스})\]

술어 논리를 명제 논리식으로 바꿔서, 명제 논리식으로 새로운 지식을 추론한다. 즉 술어를 통해서 지식을 더 체계화하는 것 뿐이다.

그래서 뭘 써야되는데?

논리보다 규칙을 통해 지식을 표현하는 방법이 더 많은 추론을 할 수 있다고 증명되어 있다. 따라서 현재는 상속 기반의 의미망, 프레임으로 지식베이스를 구축하고 있다. 딥러닝이나 LLM에선 하이브리드 방식으로 사용한다.

IT, 인공지능