인공지능 7. 유전 알고리즘

게시 2025/07/19

By 신희곤

30 분읽는 시간

인공지능 7. 유전 알고리즘

Unimodal, Multimodal, Combinatorial의 차이점이 무엇인가?

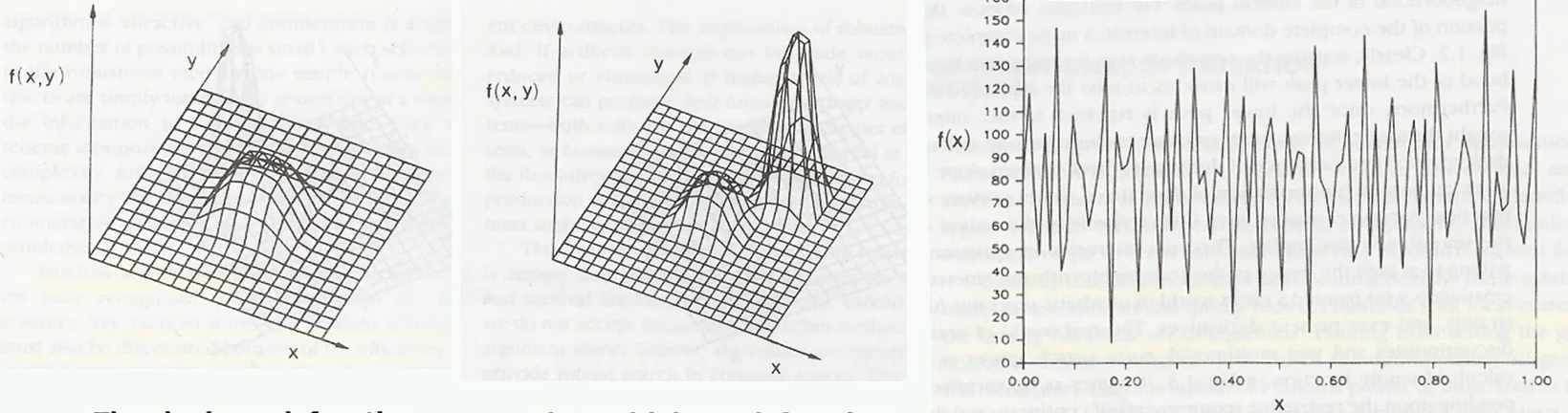
Unimodal Problem은 최적의 Peak가 하나만 존재하는 문제다. 힐 클라이밍이 최고의 알고리즘이다. Multimodal Problem은 Peak가 여러개 존재하는 문제다. 많은 경우 빔 서치를 사용한다. Combinatorial Problem은 Peak를 셀수도 없을 정도로 무수히 많은 문제다. 모든 경우를 다 따질수 없기 때문에, MCTS처럼 좋은 경우만 탐색하거나 추후 배울 Combinatorial Optimization 방법을 사용한다.

Combinatorial Problem의 Solution을 어떻게 구할 수 있을까?

많은 문제는 단일 파라미터의 최적값만 구하지 않는다. 여러개의 파라미터 Set 중, 최적의 파라미터 조합을 찾아야 한다. 예를 들어, 로봇팔의 경우 손목의 x, y, z angle, 팔꿈치의 x, y, z angle이 정의되고 팔을 뻗기 위해 필요한 각도 파라미터의 조합이 존재한다. 이렇게 최적의 파라미터 조합을 찾는 최적화를 조합 최적화 (Combinatorial Optimization) 라고 한다.

최적화란 무엇인가? 어떤 식이 존재하고, 그 식을 최적화하는 파라미터 (주로 최대, 최솟값)을 찾는 것이다. 함수 최적화란, 함수의 최대나 최솟값을 찾는 것이다. 그렇다면, 조합 최적화는 어떻게 할 수 있을까?

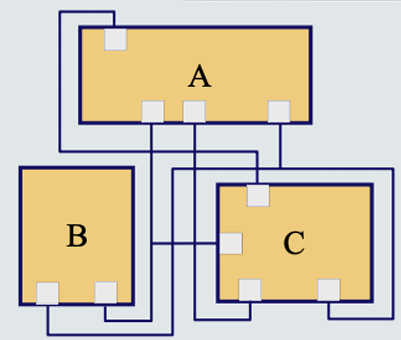
VLSI 최적화 문제에 대해 알아보자. VLSI 문제란, 기판의 위치, 포트 위치에 따라 필요한 전선의 개수, 총 길이, 각 전선의 길이 등이 달라진다. 총 전선의 길이를 최대한 짧게 하고, 각 전선이 일정 길이 이상 넘지 않도록 하는 조합을 찾아야 한다.

조합 최적화에 대해 VLSI 최적화 문제에 대해 알아보자. VLSI 문제는 회로 기판 위에 전선을 어떻게 두고 어디에 두고 어떻게 겹쳐야 가장 최적의 결과를 내는지 알아야 한다. 겹치는게 적을 수록 좋고, 선을 적게 쓸수록 좋겠지? 즉 전선 위치를 놓는 포트 위치를 어디에 둬야하는가?

먼저, 기판의 위치, 포트 위치 등을 인자값으로 받는 목적 함수 (cost function, loss function) 를 정의해야 한다. 목표는 Efficiency가 가장 큰 파라미터 조합을 찾는 것과 같다.

[!note] Efficiency란?{title} 정확도, 비용, 효율, 가성비 등 모든 것을 따져서 매기는 하나의 값이다.
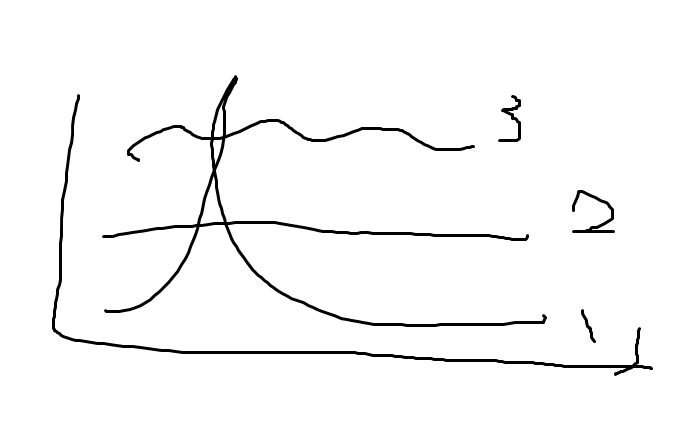
예를 들어, 위 그래프의 y축이 Efficiency라고 하자. 1번이 Hill Climbing이다. 유니모달의 경우 최고의 선택이다. 2번이 A* 알고리즘이다. 3번이 유전 알고리즘이다. 항상 무난히 괜찮다. CO Problem의 경우 A* 쓸바에 GA 쓰면 되기 때문에, A*는 절대 쓰지 않는다.

목적 함수를 최적화하기 위해, Local Search 아이디어를 사용한다. Local Search란, 임의의 시작점에서 시작하여 이웃 중 더 좋아보이는 위치로 이동한다. 이를 반복하면, 더 이상 좋아질 수 없는 위치까지 도달할 수 있다. 이웃을 방문하는 방법은 세가지로 구분할 수 있다.

First Improvement: 가장 먼저 보이는 좋아보이는 답으로 이동한다.
Best Improvement: 모든 이웃을 다 살펴보고, 그 중 가장 좋은 답으로 이동한다.
Random Walk: 랜덤으로 이동한다.

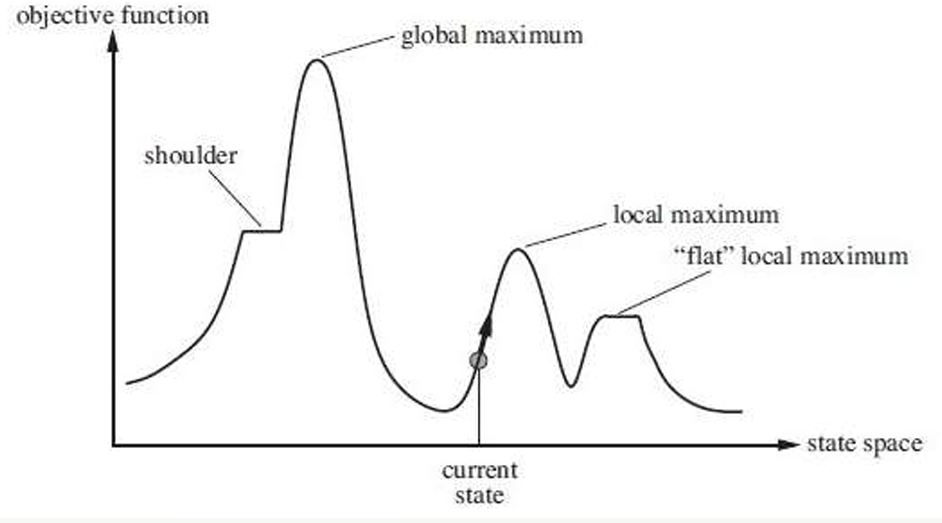
Local Search의 가장 큰 문제는, 극대 극소점 또는 flat한 곳에서 Local Optima에 빠진다는 것이다. 가장 간단히 생각할 수 있는 해결책은, Random Walk 방법을 적용하는 것다. 평소에는 Best 해로 이동하되, 가끔씩 안좋은 방향으로도 이동하게 만들면 된다. 이를 적용하면 해의 퀄리티는 좋아지지만, 해를 찾는 시간은 더 걸리기에 총 Efficiency는 떨어질 수 있다. 따라서 Local Optima를 똑똑하게 해결하기 위해 여러 알고리즘을 고안했고, 그 알고리즘들을 Metaheuristics라고 한다.

[!question] Metaheuristics의 heuristics은 heuristics function의 heuristics인가?{title} ㄴㄴ. 휴리스틱의 넓은 의미는 대충 인간의 경험적 감으로 ‘이정도면 되겠지?’ 하는걸 휴리스틱이라고 함. Metaheuristics은 100% 최적해를 찾아주지 않지만, 경험적으로 괜찮은 Solution을 찾아주는 알고리즘 집합을 뜻한다.

Metaheuristics는 단일로 Local Search하는 방법과, 집단(Population)으로 Local Search하는 방법으로 구분한다.

Local search metaheuristics
- Simulated Annealing (SA): 담금질(Annealing)에서 아이디어를 얻는다.
  - 담금질은 온도가 높을 수록 원자가 활발하게 움직이고, 낮을 수록 느리게 움직인다.
  - 온도(Temperature) 변수를 도입하여, 온도가 높으면 Random Walk으로 여러 지역을 탐험(Exploration)한다. 저온이 될 수록 좋은 해답 근처로 이동 (Exploitation)한다.
  - 더이상 좋은 해답이 나오지 않을 때까지 담금질을 반복한다.
  - 대부분 Global Optima를 찾아준다. Solution의 퀄리티가 중요하다면, SA를 사용한다.
- Tabu Search: 단기 기억 메모리를 도입한다.
  - 이웃 중 최고를 고르고, 선택한 이웃을 일정 기간동안 기억한다. 이웃 중 최고는 현재 해답보다 안좋아도 된다.
  - 다음 이웃을 탐색할 때, 기억해둔 위치를 제외한 다른 이웃으로 이동한다.
- Iterated Local Search (ISL), …
Population based metaheuristics
- Genetic Algorithm (GA): 생물의 진화 방식에서 아이디어를 얻는다.
- Scatter Search, Memetic Algorithm, Partical Swarm Optimazation (PSO), …

Genetic Algorithm이 무엇인가?

생물은 여러 개체가 만나 자손을 낳음을 반복하여 더 환경에 최적화된 방향으로 진화한다. 여기서 아이디어를 얻는다. 여러 인구(Population)를 정의하고, 진화를 거듭한다면 최적해를 찾을 수 있을 것 같다.

[!tip] 사실 Evolutionury(진화) Algorithm은 Genetic Algorithm만 있는게 아니다.{title} Genetic Algorithm 뿐만 아니라 Genetic Programming, Evolution Strategy, Evolution Programming 총 4가지가 존재한다. 지금은 GA만 사용하므로, 사실상 Evolutionury Algorithm 하면 Genetic Algorithm이긴 함.
차이점은 인코딩이 그래프나 트리냐 벡터냐, 진화 연산자가 Crossover냐 Muration이냐에 따라서 다름. GA는 인코딩이 벡터고, Crossover를 주로 사용함.

생명체가 진화를 어떻게 하는가? 두 암수가 만나 자식을 낳는다. 우월한 개체일 수록 자식을 낳을 확률이 높다. 자연선택 자식을 낳는다는 의미는 무엇인가? 부모의 두 염색체를 교차하여 자식의 염색체를 만든다. 이 과정에서 낮은 확률로 돌연변이가 생길 수 있다. 자식은 또 다음 세대의 짝을 만나 번식에 실패할 수도, 성공할 수도 있다. 이를 무수히 많이 반복한다.

위 과정을 알고리즘으로 나타내면 다음과 같다.

t = 0;
Population 초기화. P(t)
수렴 조건에 따라 다음을 반복한다.
{
    P(t)를 평가한다.
    우수한 개체 쌍을 선택한다. (Selection)
    자식을 낳는다. (Crossover)
    자식을 돌연변이 화한다. (Mutation)
    자식을 Polulation에 추가한다. (Insertion)
    t += 1;
}

이때 t는 세대를 의미한다.

그렇다면, 구현해야 하는 것은 다음과 같다.

수렴 조건을 어떻게 판단하는가?
염색체를 어떻게 표현하는가?
염색체를 평가하는 함수를 어떻게 정의하는가?
두 염색체를 어떻게 선택하는가?
두 염색체를 어떻게 교차하여 하나의 염색체로 만드는가?
돌연변이를 어떻게 만드는가?

염색체(Chromosomes)를 어떻게 표현하는가?

문제에서 조절 가능한 파라미터를 염색체로 표현해야 한다. 이를 Encoding 한다고 한다. 인코딩 기법에는 다음과 같은 방법이 있다.

Binary Encoding
Ternary, Quaternary: 3진법, 4진법 (0,1,2), (0,1,2,3)
Integer
Real Valued
Hexadecimal: 16진법: 0~9, A, B, C, D, E, F

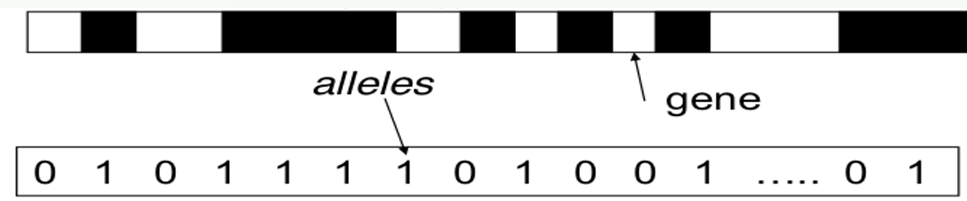
하나의 염색체(Chromosomes)는 solution에 해당하며, 각 비트는 유전자 (gene) 에 해당한다. 한 비트의 값들이 대립 유전자(allele) 에 해당한다. Chromosomes은 String 또는 Vector로 구현할 수 있다.

가장 많이 사용하는 인코딩은 Binary Encoding 기법이다. 이유가 무엇인가? 교차나 돌연변이를 만들기 아주 간단해지기 때문이다. 실제로 어떻게 인코딩하는지 살펴보자.

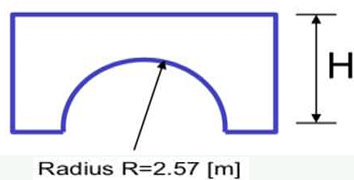
[!example] 다리 모양을 최적화{title}
가능한 파라미터 값은 높이 H와 반지름 R이다. H의 범위가 0m ~ 32m라면, H를 표현하기 위해 5비트가 필요하다. R은 0m ~ 10m까지 가능하다면, R을 표현하는데 4비트가 필요하다. (\(2^4=16 > 10\)) 따라서, Chromosomes을 9비트로 정의하여 두개를 가져다 붙이면 된다.
\[101101001\]
앞에서부터 5개의 비트를 H, 뒤의 4개의 비트를 R이라고 하자.
\[H=10110=16+4+2=22m\] \[R=1001=8+1=9m\]

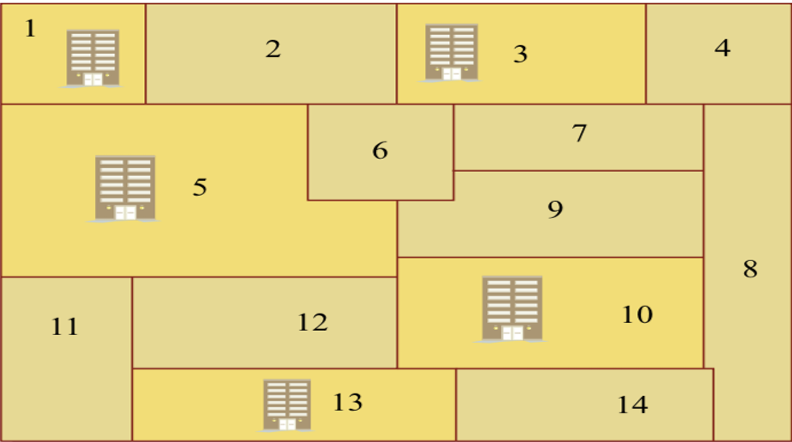
[!example] 소방서 배치 문제{title}
각 지역이 있을 때, 소방서가 몇개, 어디에 설치되어야 최적인가? 간단하게 14개 비트를 사용해서 각 지역마다 소방서가 설치되면 1, 설치가 안되면 0으로 나타낼 수 있다. 위 그림을 바이너리 코드로 나타내면 다음과 같다.
\[10101000010010\]

위와 같이 Encoding과 Decoding을 할 수 있다.

하지만 모든 문제가 항상 비트로 다 표현할 수 있는 건 아니다. 예를 들어, 외판원 문제의 경우 도시를 방문하는 순서를 int로 기록하는 방법이 더 편할 수 있다. 이미 인코딩 schemes가 많이 개발되어 있으므로, 문제에 맞게 적당한 인코딩 방법을 사용하면 된다.

Fitness and Selection를 어떻게 하는가?

Selection은 GA에서 가장 중요하고, 비용이 많이 드는 과정이다. 가장 어려운 것은 fitness function을 정의하는 것이다. 우리는 그냥 만들어진거 사용한다.

Selection 방법은 세가지가 존재한다.

(1) Ranking selection Population을 Fitness 값으로 정렬하고, 순위별로 확률을 차등 부여한다. 이후 k명을 뽑는 방법이다. 정렬을 사용하기에 연산 비용이 크다.. Fitness 값 차이가 극단적인 경우에도 안정적으로 작동하는 장점이 있다.

(2) Roulette-wheel selection or Proportionate selection Fitness 값이 높은 친구를 높은 확률로 뽑는 방법이다. Fitness 값을 양수로 정규화 해야한다.

\[Pr(h_{i}) = \frac{Fitness(h_{i})}{\sum_{j=1}^{M}Fitness(h_{j})}\]

모든 population에 대해 위 확률을 계산하고, 랜덤 숫자를 뽑아서 룰렛 판에 걸린 크로모좀을 뽑는다. 자기 자신이 여러번 선택될 수 있다.

(3) Tournament selection 임의로 k마리를 뽑아, 그 중 가장 Fitness가 높은 크로모좀을 부모로 선택한다. k는 보통 2~3으로 설정한다. 부모 수를 모두 채울 때까지 이것을 반복한다. 랜덤성이 크기 때문에, 수렴이 안될 위험성이 존재한다.

선택해야 하는 부모는 몇 명인가? population의 수를 N이라고 하자. N은 짝수라고 가정한다. Insertion Strategy에 따라 Selection해야 할 부모 수가 달라진다. 만약 세대 전체 교체라면, N마리 뽑는다. 이후 N/2 쌍의 부부를 만든다. 만약 Steady-State라면, 2명을 뽑아 한쌍의 부모만 만든다. 이후 Control Parameter로써 주어진 Crossover rate, Mutation rate를 사용해, 각 부부쌍에 대해 Crossover를 수행할건지, Mutation을 수행할건지 결정한다.

보통 Crossover rate는 0.1~0.5, Mutation rate는 0.01~0.05 정도로 설정한다. 이는 부모가 Crossover할 확률이 0.1 ~ 0.5고, 자식 쌍이 돌연변이가 될 확률이 0.01 ~ 0.05라는 뜻이다. 즉, 각 부모 쌍에 대해 랜덤 넘버를 뽑아 Crossover rate보다 낮으면 Crossover하고, 더 높으면 하지 않는 방법으로 구현할 수 있다. 만약 Crossover를 하지 않으면, 부모를 그대로 자손으로 삼는다.

왜 Crossover rate를 1로 설정해서 모든 부모를 갈아치우지 않는가? 꼭 Crossover나 Mutation을 한다고 항상 좋아지는게 아니기 때문이다. 따라서, 좋은 형질의 부모까지 갈아치우지 않고 적당히 보존시켜주는게 더 안전하다.

Crossover를 어떻게 하는가?

Chromosomes 인코딩 방식을 어떤걸 선택했는지에 따라 다른 Crossover operator를 적용해야 한다. 먼저 Binary Encoding에 대해 살펴보자. 크게 세가지 Crossover 방법이 존재한다.

(1) Single-point crossover

랜덤하게 하나의 Point를 찍는다. 그 Point를 기준으로 Cross해서 2마리의 자식 개체를 생성한다. 가장 많이 사용하는 방식이다.

(2) Multi-point crossover

2개 이상의 Point를 사용한다.

(3) Uniform crossover

각 비트 자리마다 동전을 던져서 (50%의 확률) 부모 1의 유전자를 받을지, 부모 2의 유전자를 받을지 결정한다.

[!question] 단순히 Crossover할 뿐인데 왜 결과가 최적해에 가까워지는가?{title} 만약 바이너리 인코딩을 앞의 4자리를 정보 1, 뒤의 5자리를 정보 2로 설정했다고 가정하자. 만약 2번째 자리를 Point 잡고 Crossover하면, 정보가 완전 뒤죽박죽 섞이는 것 아닌가? Crossover가 의미 없는 것 아닌가?
그럼에도 GA는 괜찮은 최적해를 찾아준다. 그 이유는, 위의 케이스처럼 안좋은 Crossover가 일어날 수도 있지만, Crossover를 했더니 운좋게 Fitness 값이 큰 자식이 생길 수도 있다. Crossover 결과로 낮은 Fitness 값을 가지는 자식은 점점 도태되고, 훌륭한 Fitness 값을 가지는 자식은 점점 살아남는다. 이를 무수히 많이 반복하면, 큰 수의 법칙에 따라 Polulation은 점점 좋은 방향으로 최적화된다.

Mutation는 어떻게 만드는가?

생성된 자식에 대해, 각 비트 자리마다 Mutation rate 확률로 비트를 뒤집는다. 이러면 아주 낮은 확률로 돌연변이 자손이 생성된다.

왜 돌연변이를 만들어야 하는가? 해공간이 아주 큰 경우, 크로스오버만 하면 특정 범위로 점점 수렴하지만, 사실 완전 다른 곳에 더 좋은 해가 존재할 수도 있다. 따라서, 가끔 다른곳을 탐색하도록 튀는 값을 부여해야 한다. 만약 돌연변이가 좋지 않은 값이면 자연스럽게 도태될 것이고, 좋은 값이면 Selection될 확률이 높으므로 Local optima에서 벗어날 수 있게 된다. 이것이 계속 반복되면, Global Optima까지 찾아낼 수 있다.

[!note] Crossover와 Mutation이 해공간 탐색에서 어떤 역할을 하는가?{title} Crossover와 Mutation은 각각 활용(Exploitation)과 탐색(Exploration)에 해당한다. Selection and Crossover은 좋은 두 부모를 뽑아서 더 좋은 자손을 만드는 것과 같다. 이를 반복하다 보면, 집단 전체가 비슷해져서 새로운 조합이 잘 안만들어진다. 수렴 지점이 Global Optima라면 원하는 결과를 얻은 것이지만, Local Optima라면 해결해야 한다.
Mutation은 위에서 설명했듯이, 새로운 가능성을 탐색하는 기회를 준다. 그러나 Mutation이 너무 자주 발생하면, 랜덤 탐색과 비슷하게 되고 수렴하지 않을 가능성이 높다.
따라서 Crossover rate와 Mutation rate를 적절히 조절해야 하고, 이것이 Exploitation과 Exploration의 밸런스를 조율하는 것과 같다.

Insertion 전략을 어떻게 세울까?

(1) 가장 단순하게 N명의 부모를 Selection해서 N마리의 자손을 생성 후 전 세대 인구를 교체하는 방법이 있다. 일부 다처제가 가능하다.

[!question] Crossover rate가 1보다 작으면 N마리보다 작은 자손이 생성될 수 있는 것 아닌가?{title} 아니다. Crossover를 하지 않아도, 부모 형질을 그대로 자손 형질로 사용하여 총 N마리의 자손이 유지된다.

(2) 또는 Selection 단계에서 2마리만 선택해서, 생성한 자손을 polulation에서 fitness 값이 가장 안좋은 개체와 교체하는 방법이 있을 수 있다.

(3) Elitist Strategy, Hall-of-frame 선택한 부모 중 가장 우수한 일정 비율의 부모는 엘리트로 설정해서, Crossover를 하지 않고 그대로 다음 세대로 물려주는 전략을 사용할 수 있음. 이 방법은 자칫하면 우수한 부모의 형질만 너무 많아지게되는 문제가 존재할 수 있기 때문에, 엘리트를 기억해서 다음 Selection에서 엘리트를 선택하지 않도록 구현할 수도 있음.

[!question] 왜 특정 형질만 남으면 문제가 되는가?{title} 특정 형질만 남는다는 것은, 해공간에서 국소 범위에 크로모좀이 몰려있다는 것과 같다. 이러면 세대를 거듭해도 총 Fitness 값의 변화가 작아진다. 돌연변이가 운좋게 일어나지 않는 이상 그대로 수렴하여 Local optima에 빠질 위험성이 있다.

Initialization를 어떻게 하는가?

Multi Modal Problem의 경우 초기 값을 잘 설정하는게 중요하다. 초기 값을 잘 지정하면 바로 Global optima를 찾을 수 있지만, 그렇지 않다면 뺑뻉 돌다가 겨우 찾을 수도 있다.

그러나 Combinatorial Problem에선 초기화가 그렇게 중요하지 않다. 그냥 골고루 뿌려주기만 하면 된다. 따라서 초기 모집단은, 그냥 랜덤한 크로모좀을 생성하면 된다.

수렴 조건(GA Convergence)을 어떻게 판단하는가?

전체 Population의 Average Fitness 값의 변화가 몇세대 거듭해도 별 차이가 없다면, 수렴되었다고 판단 할 수 있다. 또는 그냥 고정값으로 반복시켜도 된다.

Control Parameter로 어떤 값이 있는가?

Population Size
Crossover Rate
Mutation Rate

각 값은 고정값이 아니라, Dynamic하게 변화시켜도 무방하다. 예를들어, Mutation Rate를 세대에 비례하여 큰 값에서 점점 작아지도록 만들면, 초창기엔 해공간을 넓게 탐색하다가 점점 안정적으로 수렴하도록 만들 수 있다.

GA 알고리즘을 어떻게 사용하는가?

Encoding
Fitness Function 정의
Genetic operators 정의
1. Initialization, Selection, Crossover, Mutation, Insertion
2. 여러개가 있는데, 그 중 잘되는걸 선택하면 된다.
Control Parameter 설정
실행
1. 세대와 Population의 Fitness 그래프를 계속 모니터링 해야 한다.
2. 점진적으로 증가 또는 감소하다가 수렴하면 GA가 잘 작동한거고, 그래프가 요동치면 어딘가 잘못된 것이다.
답이 잘 나왔다면 Decoding
답이 잘 못나왔다면 Tuning
1. Genetic operators를 바꿔본다. 특히 selection이 중요
2. Control Parameter를 바꿔본다.

AI 엔지니어링을 한다는건 5번과 7번을 반복하는 것이다.

GA가 Robust한 이유는 무엇인가?

Robust = 강하다, 웬만해선 잘 동작한다

Domain 의존성이 낮다. Encoding만 잘 하면, 다른 문제를 같은 방법으로 풀어버릴 수 있다.
여러 Population of points를 기준으로 동시에 탐색하기 때문에, Local Optima를 피하기 유리하다.
1. 병렬 컴퓨팅을 적용하기도 유리하다. 따라서 다른 알고리즘에 비해 비교적 빠른 시간 내에 해를 찾을 수도 있다.
Local Search에서 이웃 노드로 Transition할 때 Gradient 정보를 사용하지 않으므로, f(x)가 미분이 어렵거나, f(x)가 블랙박스일 때도 사용할 수 있다.
반드시 좋은 쪽으로만 Transition하는게 아니라, 확률적으로 가기 때문에 Local Optima를 잘 빠져나올 수 있다.

외판원 문제에 대해 알아보자. 외판원 문제가 왜 조합 최적화 문제지?

IT, 인공지능