포스트

인공지능 6. Monte Carlo Tree Search

게시
By 신희곤
18 분읽는 시간
인공지능 6. Monte Carlo Tree Search

민맥스 알고리즘은 항상 제로섬 게임에서 사용할 수 있는 최고의 알고리즘인가? 그렇지 않다. (1) 휴리스틱 함수를 만들기 어렵고, (2) 깊이가 깊어질수록 넓이가 기하급수적으로 넓어지고, (3) 제한 시간 내에 최적해를 찾아내기 어렵다. 이를 해결하게 위해 Bandit-based methods를 사용한다.

Bandit-based Methods가 무엇인가?

이 방법은 원-암드 밴딧이라는 슬롯머신에서 유래한 방법이다. 어떤 슬롯머신을 돌렸을 때 가장 최고의 결과를 얻는가? 좋은 슬롯 머신을 찾기 위해 한번씩 돌려봐야 한다. 그런데 돌려보다가 돈을 다 써버리면? 말짱 도루묵이다. 만약 돌려보다가 잭팟이 터졌다! 그럼 그 슬롯머신만 쓰겠지? 그런데 그 슬롯머신이 사실 안좋은 슬롯머신인데, 우연히 잭팟이 터졌던 거일 수도 있다. 사실 확률이 더 좋은 슬롯 머신이 바로 옆에 있을 수도 있다.

새로운 슬롯머신을 테스트해보는 것이 탐험(Exploration) 이고, 좋아보이는 슬롯머신을 사용하는게 활용(Exploitation) 이다. 탐험과 활용의 밸런스를 적절히 잡아야 최고의 결과를 얻어낼 수 있다. 그 방법을 Bandit-based Method라고 말하며, UCB(Upper Confidence Bound) 와 같은 알고리즘이 수학적인 공식으로 탐험과 활용의 밸런스를 잡아준다.

Monte Carlo Tree Search가 무엇인가?

민맥스 트리의 단점을 해결하고자 Bandit-based Method를 적용한 탐색 기법이다. 어떻게 민맥스 트리의 단점을 해결하는가? 먼저, MCTS는 휴리스틱 함수를 사용하지 않는다. 대신에, 랜덤으로 수를 두는 시뮬레이션을 무수히 많이 돌려봐서 얻는 승률을 평가치로 사용한다. 그리고, 모든 가능한 수를 탐색하지 않는다. 좋아 보이는 수만 적당히 확장하기 때문에, 민맥스 트리가 산 모양으로 확장된다면 MCT는 낙하산 모양으로 확장된다. 또한, 최고의 수를 찾다가 중간에 중단해도, 지금까지 찾아둔 적당히 좋은 해 정도는 알고 있다. 즉 제한 시간 내에 적당한 해를 찾는데 용이하다.

그렇다면, MCTS는 항상 최적의 해를 찾을 수 없는 것 아닌가? 그렇지 않다. 시간만 충분히 주어진다면, MCTS는 Optima 해를 찾음이 증명되었다.

그래서 MCTS는 어떻게 State tree를 Search하는 건가? 다음 네가지 과정을 계속 반복한다.

  1. Selection: 루트 노드에서 시작하여, Tree policy 대로 확장 가능한 노드를 선택한다.
    • 확장 가능한 것은, terminal node가 아니고 탐험되지 않은 자식 노드가 있는 경우다.
    • Tree policy란, 노드를 Selection하는 정책이며 탐험과 활용의 밸런스를 조율하는 방법이다.
  2. Expansion: 만약 선택한 노드를 방문한 적이 있으면, 자식 노드를 확장한다.
    • 어떻게 확장할 것인지는 Tree policy에 따라 다르다.
  3. Simulation: 선택한 노드 또는 확장한 노드 하나를 골라 시뮬레이션을 돌린다.
    • 시뮬레이션 방법은 Default Policy가 결정한다.
  4. Backpropagation: 시뮬레이션 결과를 선택한 노드와, 모든 부모 노드에게 반영한다.

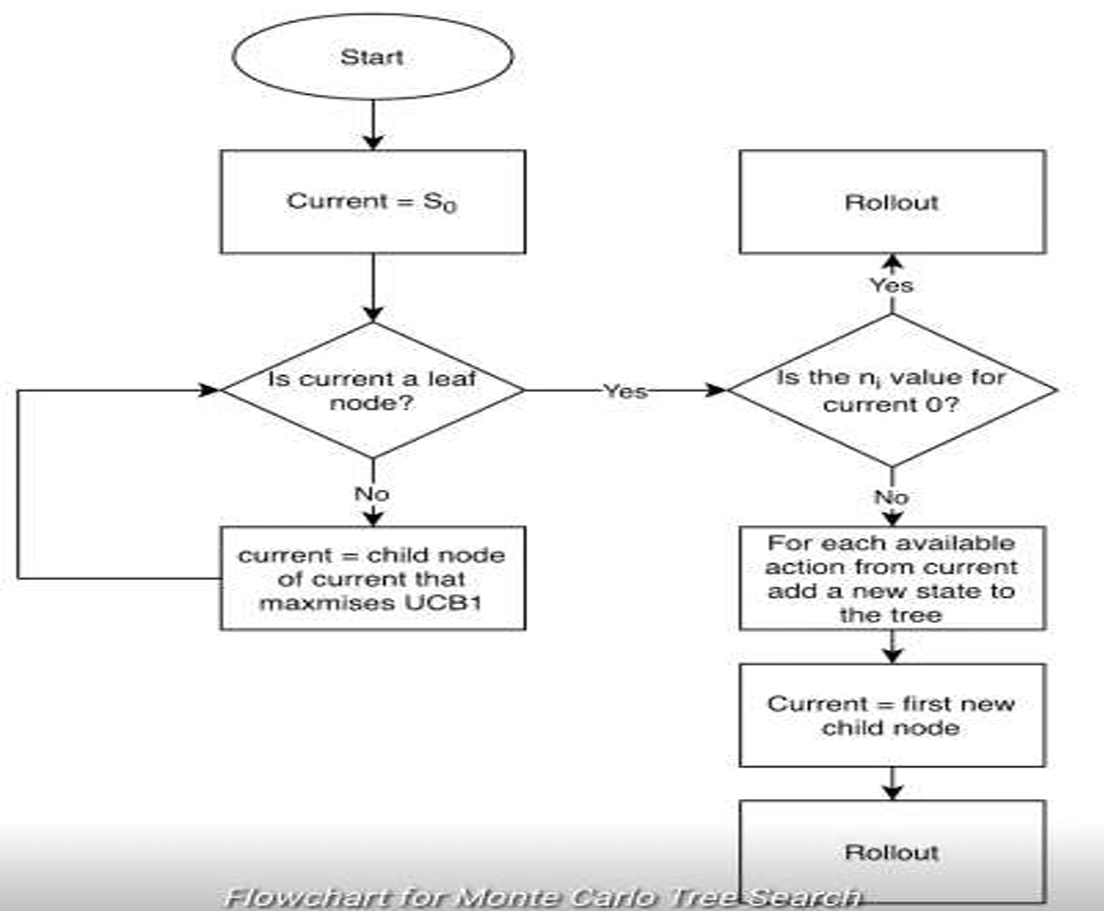
이 과정을 한눈에 보여주는 Flow Chart는 다음과 같다.

Pasted image 20250427022208.png

  1. 루트 노드에서 시작한다.
  2. 현재 선택한 노드가 리프 노드인가?
    1. 아니라면, 자식 노드중에 UCB1 값이 가장 큰 자식을 선택 후 2번으로 돌아간다.
  3. 선택한 노드가 한번도 방문하지 않은 노드인가?
    1. 맞다면, 시뮬레이션 후 백프로파게이션을 수행한다.
    2. 아니라면, MoveGenerator로 자식 노드를 확장 후 가장 첫번째 노드를 시뮬레이션 후 백프로파게이션을 수행한다.

[!tip] 시간이 끝나면, 어떤 해를 선택해야 할까?{title} 승률(가중치)이 가장 높은 해를 선택할 수도 있고, 가장 많이 방문한 (Robust) 노드를 선택할 수도 있다. 승률을 기준으로 선택하면, 잘못된 수를 둘 수도 있다. 시뮬레이션은 완전 랜덤이기 때문에, 승률이 잘못 계산될 수도 있기 때문이다. 가장 많이 방문한 노드는 그만큼 유망한 선택지이기 때문에 많이 방문했을 것이다. 이 노드를 선택하면 안전하다. 많은 경우 가중치와 방문 횟수를 모두 고려하여 선택한다. 가중치 두개를 통해 \(w_{1}M + w_{2}R\) 값이 큰 선택지를 선택할 수 있을 것이다. 그러나 가중치를 따로 튜닝해야 하는 귀찮음이 있다.

즉, 위의 과정은 고정되어 있고 우리는 Tree policy와 Default Policy만 잘 결정해주면 된다.

Tree policy로는 무엇이 있는가?

대표적으로 UCB1 Algorithm (Upper Confidence Boundary) 이 존재한다.

\[UCB 1 = \overline{X}_{j} + 2C_{p} \sqrt{ \frac{\ln n}{n_{j}} }\]
  • \(\overline{X_{j}}\) : 모든 자식 노드의 Reward를 평균낸 값.
  • \(C_{p}\) : 벨런스 상수.
  • \(n\) : 부모 노드의 방문 횟수.
  • \(n_{j}\) : 선택한 노드 \(j\)의 방문 횟수.

만약 방문 횟수가 적을 수록 두번째 항 (탐험 항)의 값이 커지게 되며, 선택될 가능성이 높아진다. 자식 노드의 Reward 평균 값이 높을 수록 첫번째 항 (활용 항)의 값이 커지게 되며, 또한 선택될 가능성이 높아진다. 이 두가지를 모두 고려한 UCB 값이 클 수록 노드가 선택될 가능성이 높아진다!

또, 게임 초반부에는 Value 값을 그렇게 신뢰할 수 없다. 좋은 노드라도 시뮬레이션 돌렸을 때 안좋은 가중치를 얻게될 수도 있고, 좋지 않은 노드라도 시뮬레이션 돌렸을 때 좋은 가중치를 얻게될 수도 있기 때문이다. 따라서 초반엔 \(n_{j}\) 값이 작으므로, 자연스럽게 탐험 위주로 수행되다가 방문이 많이 될수록 탐험 항의 값이 작아져 활용 위주로 Selection된 된다.

Default policy로는 무엇이 있는가?

시뮬레이션이란, 게임이 진행되는 하나의 경우의 수를 보는 것이다. 시뮬레이션은 수백만번은 돌려야 하므로, 아주 빨라야 한다. 따라서 수를 아무렇게나 완전 랜덤하게 두는 방법을 많이 사용한다.

실제 MCTS 알고리즘 사용을 어떻게 하는가?

먼저, tree가 root node밖에 없는 경우에서 바로 MCTS를 사용할건지, partial tree (부분 트리)를 어느정도 만들고 MCTS를 사용할건지 정해야 한다. partial tree는 보통 Depth = 1~2 정도로 만들며, 파셜 트리에서 시작하는게 훨씬 빠르기 때문에 파셜 트리를 만드는 것을 권장한다.

왜 partial tree를 만드는게 더 빠른가? 어차피 윗단계는 트리가 얼마 되지도 않아서 금방 만들 수 있는 것 아닌가? 실제로 MCTS 알고리즘이 동작하는 순서를 따라가보면 그 이유를 금방 알 수 있다.

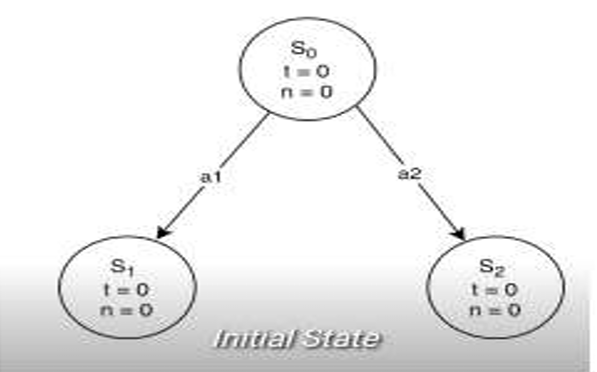
(1) 먼저, partial tree 없이 root node에서 시작하는 경우를 살펴보자.

Pasted image 20250427024614.png

각 노드는 \(\overline{V_{i}}\)와 \(n_{i}\) 값을 메모리에 가지고 있어야 한다. \(n\) 값은 어차피 역전파 적용을 위해 각 자식 노드는 부모에 대한 Pointer를 가지고 있어야 하고, 이 Pointer로 부모의 \(n_{i}\)값을 사용하면 된다. \(t\equiv\overline{V_{i}}\)라고 하자. 보통 \(\overline{V_{i}}\) 값은 \([0, 1]\) 또는 \([-1, 1]\) 사이의 값으로 정규화해서 사용하지만, 직관성을 위해 정규화하지 않겠다.

  • Iteration 1
    1. 루트 노드 \(S_{0}\)에서 시작한다.
    2. 리프 노드이고, 방문한 적 없으므로 시뮬레이션을 돌린다.
    3. 역전파를 수행한다. \(S_{0}\): \(t=0\), \(n=1\)로 바뀐다.
    4. 그런데 루트 노드를 시뮬레이션 돌린다는거 자체가 의미 없는거같은데, 보통 예외처리 할까?
  • Iteration 2
    1. 루트 노드 \(S_{0}\)에서 시작한다.
    2. 리프 노드고, 방문한 적 있으므로 자식 노드를 확장한다.
    3. 두 노드 모두 \(n=0\)이므로, \(\text{UCB1} = \infty\)이다. 이런 경우 항상 First node를 선택한다.
    4. 시뮬레이션 돌려서 \(t=20\)을 얻었다.
    5. 역전파를 수행한다.
      1. \(S_{1}: t=20, n=1\)
      2. \(S_{0}: t=10, n=2\)
  • Iteration 3
    1. 루트 노드 \(S_{0}\)에서 시작한다.
    2. 리프 노드가 아니므로, 자식 노드 중 UCB1 값이 가장 큰 노드를 선택한다. \(S_{2}\)는 방문한 적 없으므로 UCB 값이 무한이다. 따라서 \(S_{2}\)를 선택한다.
    3. 리프 노드이고, 방문한 적 없으므로, 시뮬레이션 돌린다. \(t=10\)을 얻었다.
    4. 역전파를 수행한다.
      1. \(S_{2}: t=10, n=1\)
      2. \(S_{0}: t=10, n=3\)
  • Iteration 4
    1. 루트 노드 \(S_{0}\)에서 시작한다.
    2. 리프 노드가 아니므로, 자식 노드 중 UCB1 값이 가장 큰 노드를 선택한다. \(S_{1}\), \(S_{2}\) 방문 횟수는 같고 리워드는 \(S_{1}\)이 더 높으므로, \(S_{1}\)이 선택된다.
    3. 리프 노드고, 방문한 적 있으므로 확장한다. 확장 후 첫번째 노드를 선택한다.
    4. 시뮬레이션 돌리고, 역전파를 수행한다.
  • Iteration …

알 수 있는 점은, Depth = 1에 있는 모든 노드는 한번씩 시뮬레이션 된다. Depth = 2에 있는 노드도 대부분 시뮬레이션된다. 복잡한 게임의 경우 초반에 가능한 선택지가 너무 많기 때문에, Depth 1, 2를 확장하는데 시간이 무지하게 오래 걸리게 된다.

(2) 그렇다면, partial tree가 있는 상태에서 시작하는 경우를 살펴보자. 파셜 트리는 노드마다 값이 \(\langle\text{N/A}, 0 \rangle\)로 채워진다. 싸이클을 한번 돌릴 때마다, 한꺼번에 많은 노드에 값이 채워진다. 따라서 Iteration 연산을 줄일 수 있다. 그 줄인 시간만큼 더 시뮬레이션 돌려서 더 정확한 해를 찾을 수 있게 된다.

그렇다면, partial tree는 어떻게 만드는가? 보통 게임 초반에는 수를 아무렇게나 두지 않고, 어디에 둬야 하는지 정석 수가 몇 수정도 존재한다. 예를 들어, 체스의 경우 오프닝이 있고, 오목의 경우 주형이 있음. 이 정보를 가지고 partial tree를 만들 수 있다.

항상 MCTS가 Minmax보다 좋은가? 그렇진 않다. 만약 체스와 같이 휴리스틱 함수가 뚜렷하게 정의되어 있다면, 굳이 무수히 시뮬레이션 돌리는 MCTS를 사용하지 않고 민맥스 트리를 사용하는게 나을 수 있다.

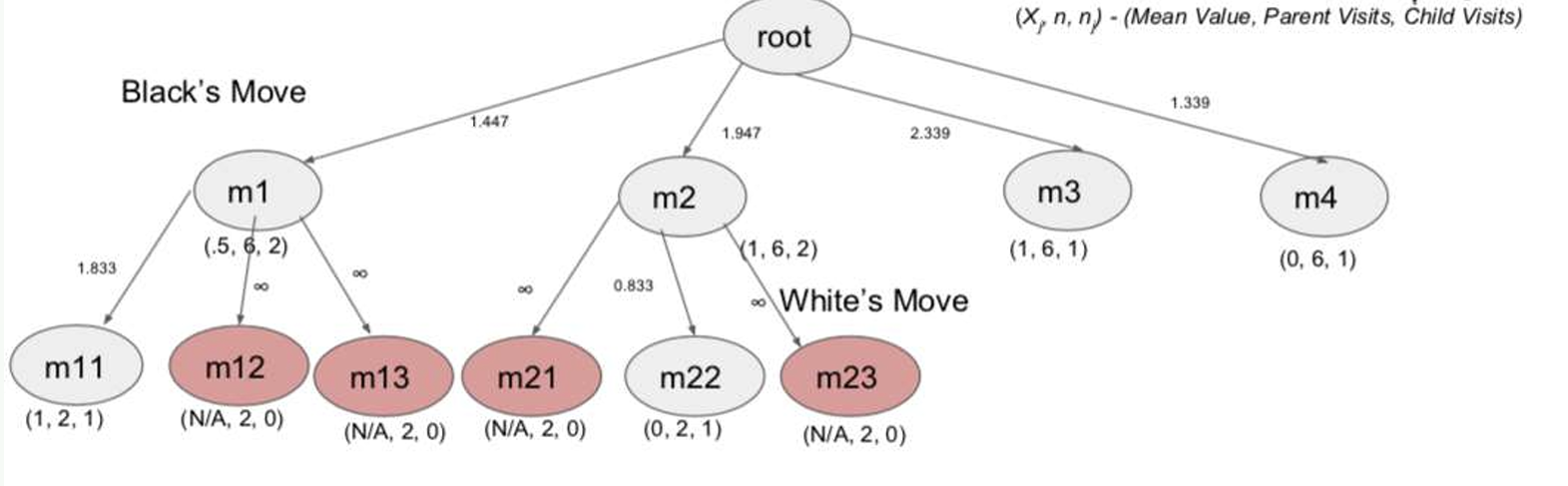
예시: 오셀로 10번 이터레이터 수행

Pasted image 20250427030837.png

  1. 위 그림은 Iteration를 6번 돌린 상태다.
  2. 빨간 노드는 아직 트리에 추가된 노드가 아니다.
  3. 10번 Iteration 돌린 후, max or robust or max-robust 기준으로 어떤 수를 선택해야 하는가?
  4. 수를 선택 후 딱 두고 나면, 그 수를 루트로 하는 아래쪽 Subtree만 남기고, 나머지 형제 가지는 전부 메모리에서 지워도 된다.

만약 멀티 플레이어의 경우 MCTS를 어떻게 적용할 수 있을까?

멀티 플레이가 될 경우, 제로섬 게임이 아니게 된다. 내가 이득을 얻어도 상대방이 꼭 손해가 아닐 수 있다. 연합의 개념을 도입해야 한다. 두 연합으로 묶는다면, 제로섬 게임처럼 만들 수 있다. 한쪽 연합이 이득을 보면, 다른쪽 연합이 손해를 본다.

하지만 연합은 게임 상황에 따라 다이나믹하게 바뀌기 때문에, 아직도 해결하고 있는 문제다.

IT, 인공지능