포스트

인공지능 2. 문제란 무엇인가

게시 업데이트
By 신희곤
14 분읽는 시간
인공지능 2. 문제란 무엇인가

에이전트는 환경에서 문제 상황을 인지하고, 그 문제 상황을 합리적으로 해결할 수 있어야 한다. 그렇다면…

문제 상황이란 무엇인가?

인공지능에서 문제 상황은 초기 상태, 목표 상태, 연산자로 표현 가능해야 한다. 연산자는 상태를 변화시키는 함수와 같다. 초기 상태에서 연산자들을 적용하여 목표 상태로 도달했다면 문제를 해결한 것이다. 초기 상태와 목표 상태는 상태 공간 위에 존재하며, 목표 상태로 도달하는 것은 상태 공간 위에서 Search(탐색)하는 것과 같다. 상태 공간이란 모든 상태가 존재하는 공간이다.

상태 공간을 어떻게 표현하는가?

상태 공간은 방향성 그래프를 사용해서 표현한다. node는 현재 상태, arc는 연산자, \(C(N_{i},N_{j})\)는 두 노드 사이의 경로 비용을 뜻한다.

상태 공간은 방향성 그래프를 사용해 표현하고, 문제를 푸는 것은 초기 상태에서 목표 상태로 도달하는 경로를 찾는 것이다. 따라서, 그래프 탐색 알고리즘 (Search)가 중요하다!

문제를 어떻게 해결하는가?

  1. 상태를 표현하는 자료구조를 정한다.
  2. 초기 상태와 목표 상태를 정한다.
  3. 규칙에 맞는 연산자(함수)를 정의한다.
  4. 상태 공간에서 초기 상태 노드에서 목표 상태 노드로 가는 경로를 탐색한다.
    1. 손으로 풀 때 : 직접 상태 공간 그래프를 그려본다.
    2. 컴퓨터로 풀 때 : 적절한 Search 알고리즘을 선택한다.

[!example]- Example 1: 문장 분석{title} 문법을 정의하고, 임의의 문자열이 문장에 속하는가? 이는 자연어 처리에서 중요한 문제다.

문장 정의

  1. Symbol a와 뒤에 놓인 Symbol b
  2. Symbol a와 뒤에 놓인 문장
  3. 문장과 뒤에 놓인 심볼 b
  4. 문장과 뒤에 놓인 다른 문장

기호 정의

  • $$는 string이다.
  • $$는 null을 포함한다.
  • \(S\)는 문장이다.

이떄 abaab가 문장인가? 판단해보자.

\[abaab = Saab = SaS = SS = S\]

문장이다.

상태 공간 그래프는 다음과 같다.

00001 (16).jpg

만약 이를 구현하려면, 상태는 string 자료구조를 사용하면 될 것이다. 초기 상태는 인풋 스트링, 목표 상태는 \(S\)이다. 위의 1~4번 규칙을 연산자로 만들면 된다.

[!example]- Example 2: 원숭이와 바나나 문제{title} 어떤 방에 원숭이, 상자 그리고 바나나가 있다. 바나나를 얻기 위하여 원숭이가 어떤 동작들을 수행해야 하는가? 원숭이는 다음 과정을 순서대로 수행해야 바나나를 얻을 수 있다.

  1. 원숭이가 상자가 있는 곳으로 가서
  2. 상자를 바나나가 있는 곳까지 밀고 가서
  3. 상자 위로 올라가
  4. 바나나를 잡아야 한다.

방의 상태는 그냥 어떤 struct로 표현하면 될 것이다. 원숭이의 위치 = v, 상자의 위치 = u, 원숭이가 상자 위에 있는지 여부 = x, 원숭이가 바나나를 가졌는지 여부 = y 등이 상태가 될수 있다. 따라서

\[(\vec{v}, \vec{u}, x, y)\]

를 하나의 상태로 나타낼 수 있다.

만약 초기에 원숭이의 위치가 \(\vec{a}\), 상자의 위치가 \(\vec{b}\)라면 초기 상태는 다음과 같다.

\[(\vec{a},\vec{b},0,0)\]

바나나의 위치가 \(\vec{c}\)라면, 목표 상태는 다음과 같다.

\[(\vec{c}, \vec{c}, 1, 1)\]

원숭이가 할 수 있는 행동은 네가지 함수로 만들 수 있다. 이것이 연산자에 해당한다.

  1. goto(u) : 원숭이가 위치 u로 이동한다.
  2. pushBox(u) : 원숭이가 상자를 u 위치로 밀고 간다.
  3. climbBox() : 상자 위로 올라간다.
  4. grasp(u) : 바나나를 잡는다.

연산자의 결과는 항상 같지 않고, 현재 상태 변수에 따라 다른 결과를 낼 수 있다. 이렇게 변수에 따라 달라지는 연산자들의 집합을 스키마(schema)라고 한다. 상태 변수를 스키마 변수(schema variable)라고 표현한다.

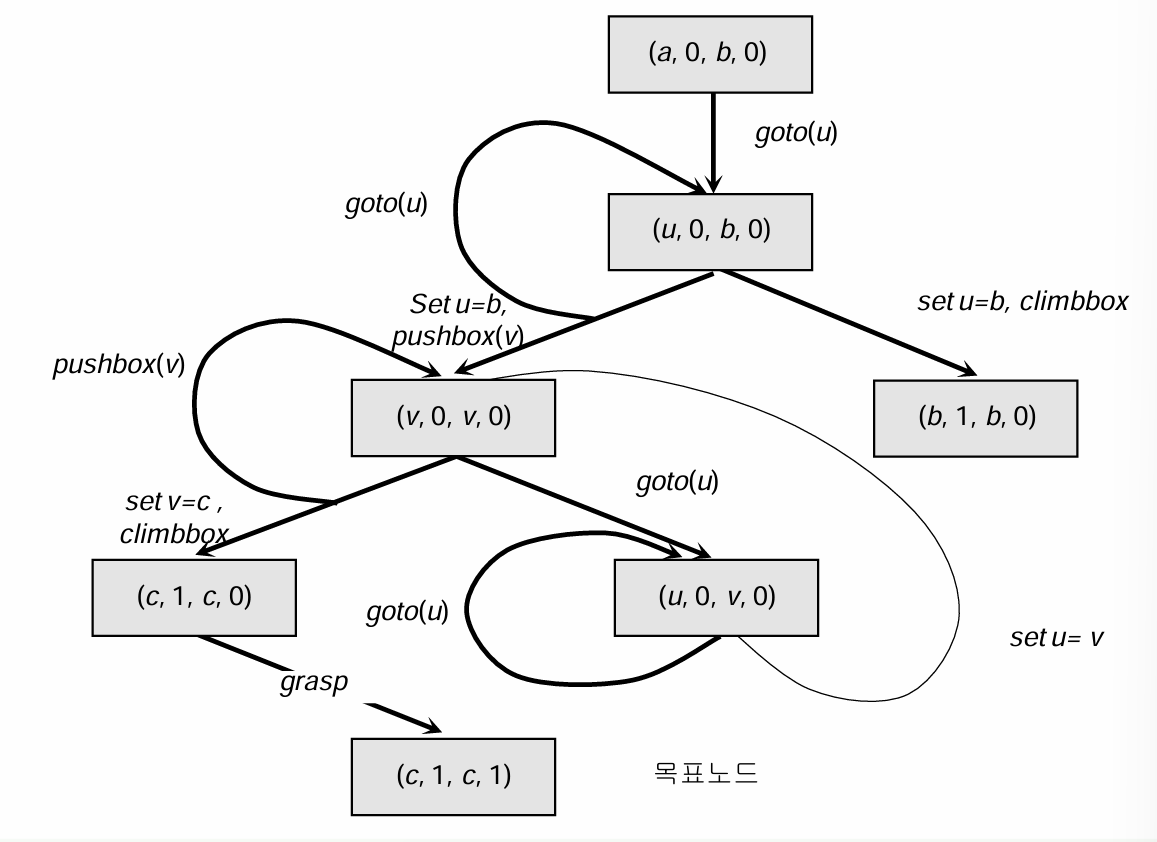
상태 공간 그래프를 그리면 다음과 같다.

Pasted image 20250410140232.png

[!example]- Example 3: 선교사 식인종 문제{title} Pasted image 20250410150332.png

3명의 선교사와 3명의 식인종이 나룻배를 타고 강을 건너려고 하는데, 나룻배에는 최대 2명 밖에 탈 수 없다. 만약 강의 어느 쪽에서라도 식인종의 수가 선교사의 수보다 많으면 식인종들은 선교사를 잡아먹게 된다. 이때 선교사들이 잡혀 먹히지 않고 6명이 무사히 강을 건너려면 어떻게 해야 하는가?

상태는 왼쪽 선교사의 수, 왼쪽 식인종의 수, 오른쪽 선교사의 수, 오른쪽 식인종의 수, 배의 위치로 설정하면 될 것 같다.

\[(\text{왼쪽 선교사, 왼쪽 식인종, 오른쪽 선교사, 오른쪽 식인종, 배의 위치})\]

초기 상태와 목표 상태는 다음과 같다.

\[\text{초기 상태:} ~~(3, 3, 0, 0, L)\] \[\text{목표 상태:}~~(0,0,3,3,R)\]

연산자는 왼쪽으로 선교사 or 식인종을 태워 이동하는 것과, 오른쪽으로 선교사 or 식인종을 태워 이동하는 것이 있다.

  • \(ML(x, y)\) : 선교사 x, 식인종 y명, 배를 왼쪽으로 이동
  • \(MR(x,y)\) : 선교사 x, 식인종 y명, 배를 오른쪽으로 이동 제약 조건은 \(1 \leq x+y \leq 2\)이며, 한쪽에 선교사보다 식인종의 수가 많으면 바로 종료 상태가 될 수 있다.

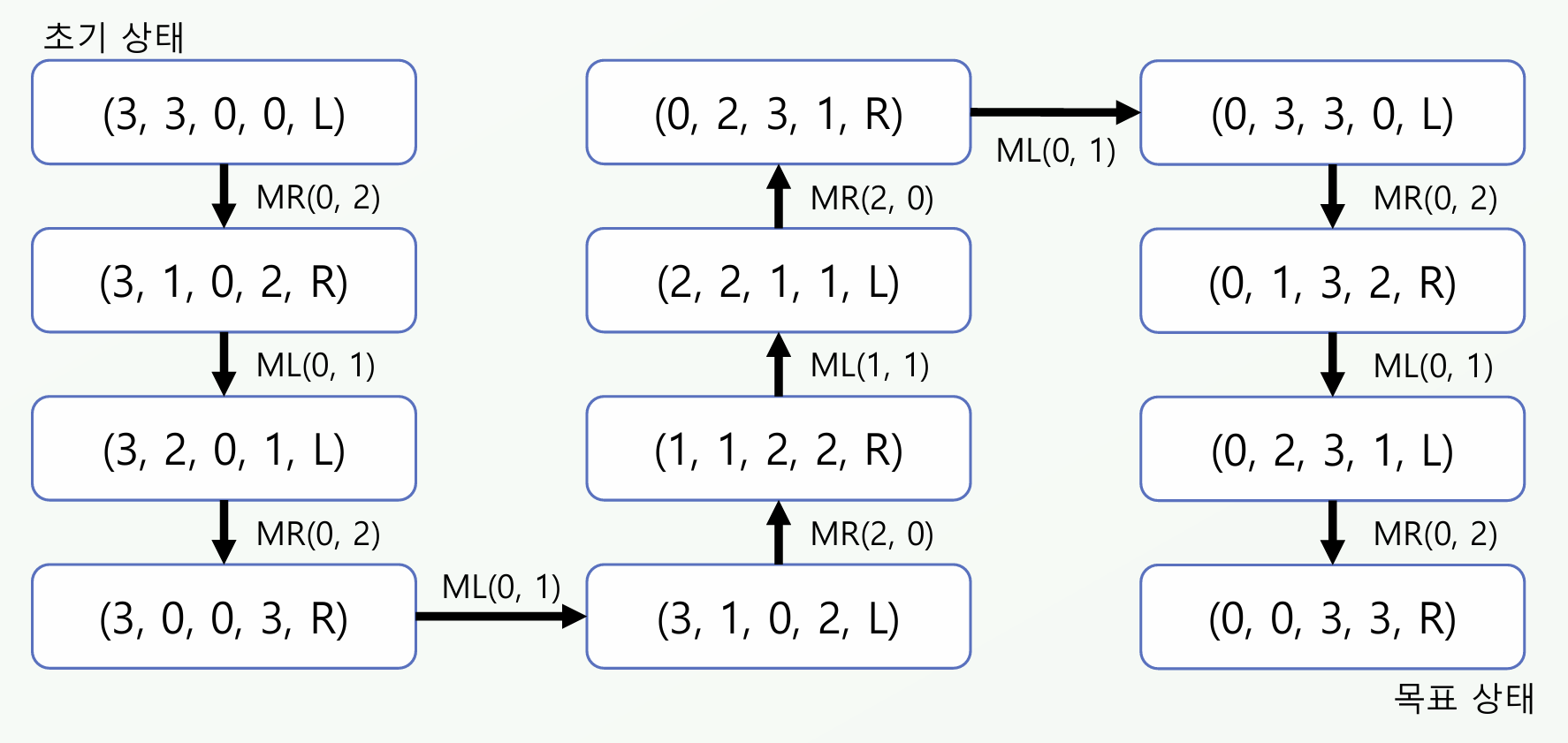
상태 공간을 그리면 다음과 같다.

Pasted image 20250410151724.png

대칭성이 존재한다. Key Operator는 \(ML(1,1)\)을 반드시 지나야 한다. 따라서 문제를 절반으로 분할하여 풀면, 나머지는 대칭해주면 문제를 풀게 된다. Key Operator를 찾았더니 효율이 두배 올랐다!

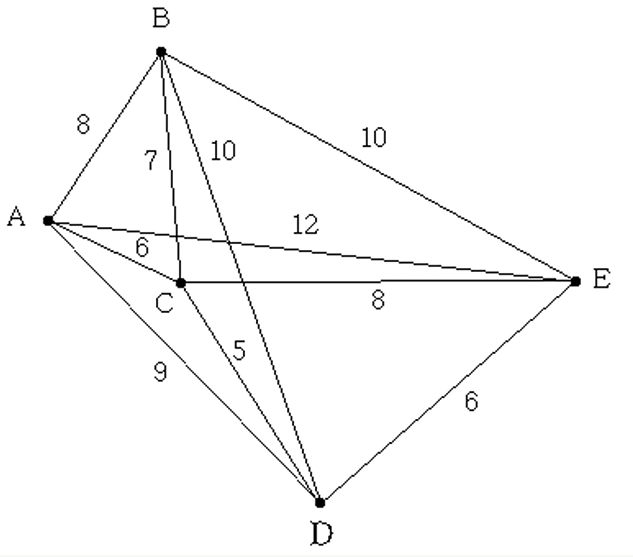
[!example]- Example 4: 외판원 문제{title} Pasted image 20250410152729.png

여러 도시들이 있고 한 도시에서 다른 도시로 이동하는 비용이 모두 주어졌을 때, 모든 도시들을 단 한 번만 방문하고 원래 시작점으로 돌아오는 최소 비용의 이동 순서를 구하라.

상태는 방문하는 도시를 리스트로 표현하면 된다. 시작 조건은 \((A)\)이고, 종료 조건은 다음과 같다.

  1. 같은 도시를 두번 이상 방문
  2. 모든 도시를 한번씩 방문 두번째 종료 조건이 목표 상태와 같다.

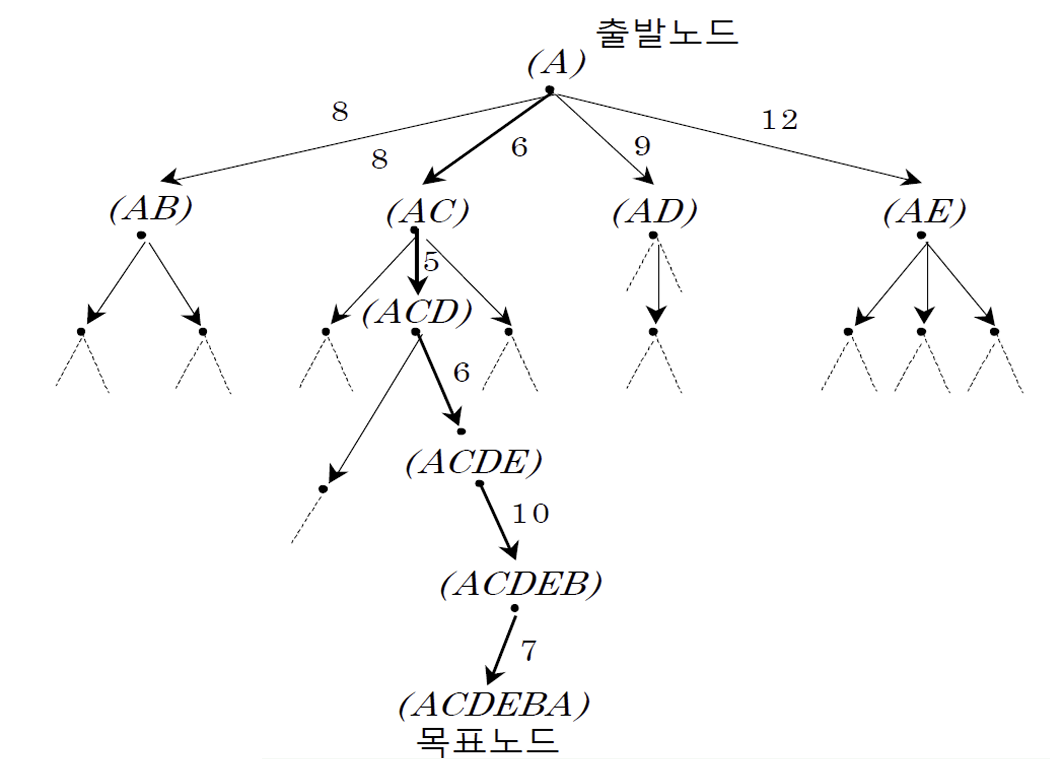
연산자는 인접한 노드로 이동하는 것이고, 그때 비용이 든다. 상태 공간은 다음과 같다.

Pasted image 20250410152851.png

상태 공간이 너무 거대해서 손으로 그릴 수가 없다! 이럴땐 상태 공간을 축소하거나, 컴퓨터를 사용해 문제를 풀어야 한다.

상태 공간이 너무 크면 어떻게 하냐?

문제 축소를 해야한다. 문제 축소의 핵심은, 반드시 지나야 하는 상태를 먼저 찾는 것이다. 초기 상태 -> 반드시 지나야 하는 상태로 문제를 부분 문제로 분할하면 문제가 축소된다.

원숭이 예제로 예를 들면, 반드시 지나야 하는 상태는 네가지가 존재한다.

  1. 원숭이와 상자의 위치가 같아지는 상태
  2. 상자를 갖고 바나나 밑으로 이동하는 상태
  3. 바나나 밑에서 상자 위로 올라가는 상태
  4. 바나나 위치에서 상자 위로 올라와서 바나나를 그랩하는 상태

반드시 지나가야 하는 상태로 가는 연산자는 Key Operator라고 부른다. Key Operator를 잘 찾으면 문제를 분할하여 생각할 수 있고, 문제를 분할하여 따로따로 풀면 병렬성을 통해 시간을 절약할 수 있다. 또, 의미 없는 상태 공간을 날려버릴 수 있어 메모리적으로도 효율이 좋다. 따라서 찾을 수 있으면 key Operator를 반드시 찾자!

상태공간 그리기 귀찮다. 컴퓨터가 알아서 탐색해서 답을 찾을 수 있게 가능할까?

물론 가능하다. Search 기법은 크게 맹목적 탐색과 경험척 탐색으로 나뉜다. 무슨 차이인가?

  • 맹목적 탐색 (uninformed search) : 정해진 규칙을 맹목적으로 따라 상태 공간을 탐색하는 기법이다. 마치 눈 가리고 더듬더듬 찾아가는 것과 비슷해 blind search라고 말하기도 한다.
  • 경험적 탐색 (informed search) : 휴리스틱 함수를 사용해서 탐색 효율을 높히는 기법이다.

또, 문제 상황에 따라 아무 해를 찾으면 장땡인 상황이냐, 반드시 최적해를 찾아야 하는 상황이냐에 따라서 다른 탐색 알고리즘을 선택해야 할 것이다.

맹목적 탐색으로 다음과 같은 알고리즘이 있다.

  • 깊이 우선 탐색 (depth-first search, DFS)
  • 넓이 우선 탐색 (breath-first search, BFS)
  • 균일 비용 탐색 (uniform cost search)
  • 반복적 깊이심화 탐색 (interative-deepening search)
  • 양방향 탐색 (bidirectional search)

경험적 탐색으로 다음과 같은 알고리즘이 있다.

  • 언덕 오르기 (hill-climbing)
  • 최상 우선 탐색 (best-first search)
  • A* 알고리즘 (a* algorithm)
  • 빔 탐색 (beam search)

결론부터 말하자면, 어떤 문제를 풀더라도 강조표시한 알고리즘이 우선적 고려 대상이다.

IT, 인공지능