인공지능 14. Q-Learning이란

Q러닝이 무엇인가?

Q러닝은 에이전트가 사전 지식 없이, 시행착오를 통해 환경과 상호작용하며 가장 큰 보상을 얻는 경로를 스스로 탐색하는 강화학습 알고리즘이다.

그게 어떻게 가능할까?

Q러닝은 현재 상태를 알면 미래 상태를 알 수 있다는 마르코프 성질에 기반한다. 즉, 과거 상태를 고려하지 않고 현재 상태만을 고려한다. 그리고 현재 상태에서 어떤 행동을 취했을 때 어떤 보상을 제일 크게 받는지 랜덤하게 시행착오한다. 그 결과를 학습하며, 최종적으로 가장 큰 보상을 받는 경로를 찾아낸다.

따라서 우리가 명시적으로 정의해줘야 하는 것은 상태, 행동, 보상이다.

상태를 어떻게 정의하는가? 상태는 딱 필요한 정보만 사용자가 잘 정의하면 된다. 보통 인덱스나, Feature vector를 사용한다.

행동을 어떻게 정의하는가? 행동이란 특정 상태에서 취할 수 있는 모든 동작이다.

\[\text{Actions}(s) = \{ A_{1}, A_{2}, \dots \}\]

현재 상태에서 다음 상태로 넘어가기 위한 모든 행동을 생각해보고, 연산자를 정의한다.

\[\text{Result(s,a)} = s_{r}\]

연산자는 상태 \(s\)에서 행동 \(a\)를 취했을 때, 결과 상태 \(s_{r}\)를 반환한다.

보상을 어떻게 정의하는가? 보상은 간단하게 정의한다. 행동을 통해 확실하게 옳은 상태로 갔다면 + 보상을 부여하고, 확실하게 옳지 않은 상태로 갔다면 - 보상을 부여한다.

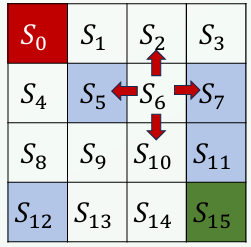
[!example] Frozen Lake − 에이전트는 시작 지점부터 얼음위를 걸어서 종료지점에 도달해야 함{title}

상태는 \(\{ S_{0}, S_{1}, \dots, S_{15}\}\)이다. 에이전트가 각 상태에서 가능한 행동은 \(\{ \text{right, left, up, down} \}\)이다. 연산자는 행동으로 인한 함수를 정의한다.

\[\text{Result}(S_{i}, \text{right}) = S_{i+1}\] \[\text{Result}(S_{i}, \text{left}) = S_{i-1}\] \[\text{Result}(S_{i}, \text{up}) = S_{i - 4}\] \[\text{Result}(S_{i}, \text{down}) = S_{i + 4}\]

그리고 보상은, 목표한 칸으로 도달하면 \(R=1\), 구멍에 빠지면 \(R=-1\), 얼음 위를 걸으면 \(R=0\)으로 부여한다.

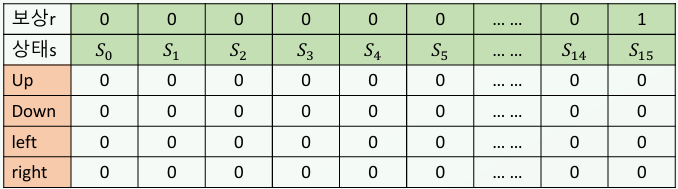
학습에 대해 알아보자. 먼저 \(Q(s,a)\) 함수를 정의한다. 이 함수는, 상태 \(s\)에서 행동 \(a\)를 취했을 때 받을 수 있는 보상의 Quality를 의미한다. \(Q(s,a)\)는 테이블로 저장 가능하다. 이를 Q-Table이라 한다.

에이전트는 탐색하거나, 활용하거나 두가지 선택지가 가능하다. 활용을 선택하면, 현재 상태 \(s\)에서 가장 퀄리티가 좋은 보상의 행동 \(a\)를 선택한다.

\[\text{arg}\max_{a} Q(s,a)\]

탐색을 선택하면 \(Q\) 함수가 업데이트된다. 어떻게 업데이트할까? 먼저 현재 상태 \(s\)에서 가능한 모든 행동 중 무작위를 하나 선택한다. 그 행동을 \(a\)라고 하면, \(Q(s,a)\)를 업데이트하게 된다.

현재 상태 \(s\)에서 행동 \(a\)를 취하면, 보상 \(r\)을 받을 것이다. 그리고 이동한 다음 상태 \(s'\)의 \(Q(s',a')\) 기대치가 높다면, \(Q(s,a)\)는 좋은 보상 퀄리티를 갖는다.

\[Q(s,a) = r + \max_{a'}Q(s',a')\]

그리고, Frozen Lake 문제를 생각해보면 경로를 삥삥 돌아서 목표에 도착하는 것보다 빨리 도착할 수록 좋은 해다. 즉, 보상을 빨리 받을수록 좋다. 나중에 받는 보상일 수록 보상의 퀄리티를 낮춰야한다. 때문에 따라서 할인 계수 (감쇠 계수) \(\gamma\)를 도입한다.

\[Q(s,a) = r + \gamma\max_{a'}Q(s',a')\]

\(\gamma < 1\)로 설정한다. 그 값은 고정값이어도 된다.

만약 외부 랜덤 요인때문에 연산자가 결정적이지 않다면? 즉, 연산자가 같은 출력값에 대해 다른 출력값을 가질 수 있다면? 이를 비결정적인(Nondeterministic) 환경이라 한다. 이 경우 \(Q\)값을 한번에 갱신하는 것보다, 기존의 \(Q\)값을 유지하며 점진적으로 개선하는 방법을 사용한다.

\[Q(s,a) = (1-\alpha)Q(s,a) + \alpha(r + \gamma \max_{a'}Q(s',a'))\]

\(\alpha\)를 학습률이라고 한다. 위 식이 일반적인 \(Q(s,a)\)이며, 결정적인 환경이면 \(\alpha = 1\)과 같다.

어떤 기준으로 활용, 탐색을 선택할까? 0과 1 사이의 랜덤 숫자를 뽑는다. 이후 설정된 기준 값 \(\epsilon\)를 설정하고, \(\text{rand} < \epsilon\)면 탐색한다. 그렇지 않으면, 해를 이용한다. \(\epsilon\)값은 \(Q\)를 업데이트하는 과정 중에 계속 감소시켜 초반에 많은 탐색을 하도록 만들고, 후반엔 탐색을 줄이도록 구현한다. (decaying E-greedy 기법)

for i in range(1000):
    e = 0.1 / (i + 1)   # 에피소드가 늘 수록 ε ↓
    
    if rand < e:
        a = random
    else:
        a = argmax(Q(s,a))

---

초기 상태에서 시작해서, 활용과 탐색을 반복하여 한번의 시행착오를 거친다. 이 시행착오를 무수히 많이 반복하여 \(Q(s,a)\)를 업데이트한다. 이 과정이 무수히 많이 반복되면, 최적 \(Q\)값으로 수렴된다.