인공지능 13. 마르코프 성질이 무엇인가
마르코프 성질이 무엇인가?
현실 세상에는 직전의 상태가 다음 상태를 결정짓는 경우가 많다. ‘오늘 날씨가 흐렸으니 내일은 비가 올 것 같다’와 같이 말이다. 미래의 상태가 현재의 상태에만 의존하는 성질을 마르코프 성질이라고 한다.
즉, 현재의 상태를 알고 있으면 미래를 예측하는 예측 모델을 만들 수 있다. 어떻게 예측할 수있을까?
먼저 상태를 정의한다. 그리고 상태가 다음 상태로 전이될 확률이 얼만지 지정한다. 이를 조건부 확률로 나타낼 수 있다.
\[p_{ij} = P(\text{다음상태} = j, \text{현재상태 = i})\]상태와 상태 전이 확률을 정의하면, 상태 전이도를 그릴 수 있다. 예를들어, 상태 전이 확률이
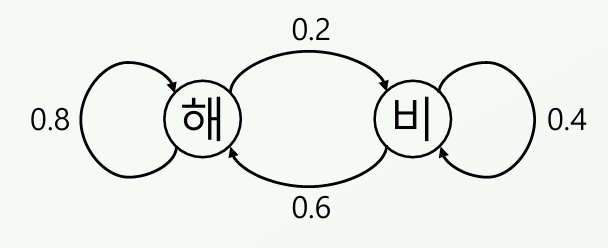
\[P(\text{다음상태 = 비}\mid \text{현재상태 = 비} = 0.4)\] \[P(\text{다음상태 = 해}\mid \text{현재상태 = 비} = 0.6)\] \[P(\text{다음상태 = 비}\mid \text{현재상태 = 해} = 0.2)\] \[P(\text{다음상태 = 해}\mid \text{현재상태 = 해} = 0.8)\]와 같을 때 상태 전이도는
와 같다. 현재 상태에 대응하는 모든 상태 전이 확률의 합은 1이다. 현재 상태가 비일 때, 0.4 + 0.6 = 1, 현재 상태가 해일 때, 0.8 + 0.2 = 1
전이 확률은 행렬로 나타낼 수 있다. 행은 현재 상태, 열은 내일 상태로 정의하자. 즉, 동일 행의 확률의 합이 1이어야 한다.
\[P = \begin{pmatrix} 0.8 & 0.2\\ 0.6&0.4 \end{pmatrix}\][!example] 예제 1{title} 동전 1과 동전 2가 있다. 동전 1을 던져 앞면이 나올 확률은 0.7, 동전 2를 던져 앞면이 나올 확률은 0.6이다. 하루에 동전을 하나 골라 한번 던진다. 만약 오늘 앞면이 나오면 내일 동전 1을 던지 고, 오늘 뒷면이 나오면 내일 동전 2를 던진다.
\[\{ \text{동전 1 던짐}, \text{동전 2 던짐} \} = \{ S_{1}, S_{2}\}\]
- 모든 상태를 나열하시오.
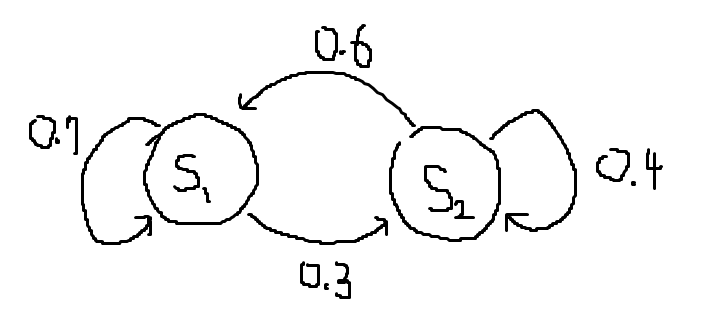
\[P(\text{내일} = S_{1} \mid \text{오늘} = S_{1}) = 0.7\] \[P(\text{내일} = S_{2} \mid \text{오늘} = S_{1}) = 0.3\] \[P(\text{내일} = S_{1} \mid \text{오늘} = S_{2}) = 0.6\] \[P(\text{내일} = S_{2} \mid \text{오늘} = S_{2}) = 0.4\]
- 상태 전이 확률을 정의하시오.
\[P = \begin{pmatrix} 0.7 & 0.3 \\ 0.6 & 0.4 \end{pmatrix}\]
- 전이 확률 행렬을 나타내시오.
행: 현재 상태 열: 내일 상태
- 상태 전이도를 그리시오.
[!example] 예제 2{title} 월요일에 해가 날 확률은 50%다. 화요일, 수요일, 목요일, 금요일의 날씨는 아래와 같은 마르코프 체인을 따른다. 월화수목금 날씨가 “해비비해해”로 나타날 확률을 구하시오
\[P(\text{월=해})P(\text{비}\mid\text{해})P(\text{비}\mid\text{비})P(\text{해}\mid\text{비})P(\text{해}\mid\text{해})\] \[= 0.5 \times 0.2 \times 0.4 \times 0.6 \times 0.8 = 0.0192\]
2스탭 뒤의 확률은 \(P^2\), n스탭 뒤의 확률은 \(P^n\)으로 계산 가능하다. 만약 \(n \to \infty\)로 보내면, 특정 상태로 수렴될 수 있다.
\[P = \begin{pmatrix} 0.8 & 0.2 \\ 0.6 & 0.4 \end{pmatrix} \implies P^2 = \begin{pmatrix} 0.76 & 0.24 \\ 0.72 & 0.28 \end{pmatrix} \implies \dots \implies P^n = \begin{pmatrix} 0.75 & 0.25 \\ 0.75 & 0.25 \end{pmatrix}\]따라서 해 뜨는 날이 75%, 비오는 날이 25%라고 추측할 수 있다.
\[P = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0.3 & 0.4 & 0.3 & 0 \\ 0 & 0.3 & 0.4 & 0.3 \\ 0 & 0 & 0 & 1 \end{pmatrix} \implies P^n = \begin{pmatrix} 1 & 0 & 0 & 0 \\ \frac{2}{3} & 0 & 0 & 0 \\ \frac{1}{3} & 0 & 0 & \frac{2}{3} \\ 0 & 0 & 0 & 1 \end{pmatrix}\]전이 확률 행렬을 보면, 확률이 0으로 수렴하는 칸과 특정 값으로 수렴하는 칸이 있다. 이를 구분하기 위해 3가지 개념을 도입한다.
- Accessible (방문 가능한) = 상태 i에서 j로 이동할 수 있는 경로가 있다면, 상태 j는 i에서 방문 가능하다.
- Recurrent = 상태 \(i\)에서 accessible인 \(^\forall j\)에 대해, \(^\forall j\)가 \(i\)로도 Accessible하면 Recurrent한 상태다.
- \(^\exists j\)에 대해서 하나라도 \(i\)로 Accessible하지 못하면, Transient 상태다.
- Transient = Recurrent한 상태가 아니면 Transient하다.
상태 전이를 무한번 해버리면, Recurrent 상태는 어떤 확률로 수렴하고, Transient 상태는 0으로 수렴하게 될 것이다. 그 이유는, Transient 상태는 재귀적 방문이 불가능하므로 스텝이 늘어날 수록, 그 상태를 방문할 확률이 점점 줄어들기 때문이다.
[!example] 다음 마르코프 체인 중에서 모든 recurrent 상태를 고르시오.{title}
상태 1의 Accessible한 상태는 1이므로, Recurrent이다. 상태 2의 Accessible한 상태는 1, 2, 3, 4인데 1, 3, 4에서 다시 되돌아올 수 없으므로 Transient 상태다. 상태 3의 Accessible한 상태는 3, 4인데 둘다 다시 3으로 올 수 있으므로 Recurrent 상태다. 상태 4의 Accessiable한 상태는 3, 4인데 둘다 다시 4로 올 수 있으므로 Recurrent 상태다.
\(A(i)\)는 상태 \(i\)에서 accessible한 모든 상태들의 집합이라고 하자. 만약 상태 \(i\)가 recurrent 상태라면 \(A(i)\)는 recucrent class다.
[!example] 모든 Recurrent class를 찾으시오.{title}
\[A(1) = \{ 1 \}\] \[A(2) = \{ 1, 2, 3, 4 \}\] \[A(3) = \{ 3, 4 \}\] \[A(4) = \{ 3, 4 \}\]\(i=2\)를 제외한 나머지 상태는 Recurrent 상태다. 따라서 \(\{ 1\}, \{ 3, 4 \}\)가 Recurrent class이다.
Recurrent class의 성질은 다음과 같다.
- 최소 하나의 recurrent 상태가 존재한다.
- Recurrent 상태들은 recurrent class로 구분된다.
- transient 상태는 유한 횟수만 방문된다.
- recurrent class 안에서는 무한히 반복 방문이 일어난다.
- n이 커질수록 recurrent class에 머무를 확률이 1에 가까워진다.
[!example] 문제{title} 동전 1과 동전 2가 있다. 동전 1을 던져 앞면이 나올 확률은 0.7, 동전 2를 던져 앞면이 나올 확률은 0.6이다. 하루에 동전을 하나 골라 한번 던진다. 만약 오늘 앞면이 나오면 내일 동전 1을 던지 고, 오늘 뒷면이 나오면 내일 동전 2를 던진다. 첫날에 던질 동 전은 랜덤으로 선택한다 (첫날 동전 1 혹은 동전 2를 선택할 확 률은 각 50%다).
\[P = \begin{pmatrix} 0.7 & 0.3 \\ 0.6 & 0.4 \end{pmatrix}\]
- 셋째날에 동전 1을 던질 확률은 얼마인가? 전이 행렬은 다음과 같다.
2단계 후 전이 행렬은 다음과 같다.
\[P^2 = \begin{pmatrix} 0.7 & 0.3 \\ 0.6 & 0.4 \end{pmatrix} \begin{pmatrix} 0.7 & 0.3 \\ 0.6 & 0.4 \end{pmatrix} = \begin{pmatrix} 0.67 & 0.33 \\ 0.66 & 0.34 \end{pmatrix}\]위 행렬은 첫째날 -> 셋째날로 전이하는 행렬이다. 즉 첫째날에 동전을 선택하는 두가지 경우가 존재하고, 각각의 경우에 대한 동전 1을 선택할 확률을 계산해 더하면 된다.
\[P(\text{동전 1}) \times 0.67 = 0.5 \times 0.67 = 0.335\] \[P(\text{동전 2}) \times 0.66 = 0.5 \times 0.66 = 0.33\] \[\therefore ~~ 0.335 + 0.33 = 0.665\]\[P^3 = \begin{pmatrix} 0.67 & 0.33 \\ 0.66 & 0.34 \end{pmatrix}\begin{pmatrix} 0.7 & 0.3 \\ 0.6 & 0.4 \end{pmatrix} = \begin{pmatrix} 0.667 & 0.333 \\ 0.666 & 0.334 \end{pmatrix}\]
- 만약 월요일에 던진 동전이 앞면이 나왔다면, 같은 주 금요일에 던진 동전도 앞면이 나올 확률은 얼마인가? 월요일에 던진 동전이 앞면이 나왔다면, 화요일은 100% 동전 1을 던진다. 즉 화 -> 금으로 가는 3스탭 전이행렬이 필요하다.
금요일에 던진 동전이 앞면이 나올 확률은 다음과 같다.
\[P(\text{금 앞면}) = P(\text{금 동전 1}) \times P(\text{앞면 \mid 동전 1}) + P(\text{금 동전 2}) \times P(\text{앞면 \mid 동전 2})\] \[= (0.667 \times 0.7) + (0.333 \times 0.6) = 0.4669 + 0.1998 \simeq 0.6667\]