인공지능 12. 베이지안 추론이란

베이지안 추론이 무엇인가?

베이지안 추론이란 증거를 근거하여 어떤 가설이 얼마나 정확한지 확률로 추론하는 추론 방법이다. 이 베이지안 추론에 베이스 정리를 사용한다. 베이스 정리을 근거해서 베이지안 분류기를 만들 수 있다. 베이지안 분류기는 분류모델의 시초격이다.

베이지안 분류기는 어떤 데이터를 가장 확률이 높은 클래스로 분류하는 모델이다. 학습이 완료되어 이미 지식을 가지고 있는 베이지안 분류기에, 새로운 데이터를 넣으면 그 데이터와 가장 적합한 클래스로 분류가 가능하다.

베이지안 분류기가 어떻게 데이터를 분류하는가? 분류 방법에 따라 최소 오류 베이지안 분류기, 최소 위험 베이지안 분류기로 구분한다.

최소 오류 베이지안 분류기란?

최소 오류 베이지안 분류기란 잘못된 클래스로 분류할 방법을 최소화하는 분류기다. 즉, 오류 확률을 최소화 하도록 분류한다. 만약 입력 데이터 \(\mathbf{x}\) 에 대한 클래스 \(\omega_{1}\)의 사후 확률이 0.7이면, 그만큼 잘못 분류할 확률은 0.3과 같다. 이 잘못 분류할 확률이 오류 확률이다. 오류 확률을 최소화하려면, 사후 확률이 가장 큰 클래스 \(\omega_{i}\)를 선택하면 된다.

만약 클래스가 \(\omega_{1}, \omega_{2}\) 두개일 때 최소 오류 베이지안 분류기의 분류 규칙은 다음과 같다.

\[P(\omega_{1}\mid\mathbf{x}) > P(\omega_{2}\mid\mathbf{x})\text{이면, } \mathbf{x} \text{를 } \omega_{1} \text{로 분류하고,}\] \[P(\omega_{1}\mid\mathbf{x}) < P(\omega_{2}\mid\mathbf{x})\text{이면, } \mathbf{x} \text{를 } \omega_{2} \text{로 분류하라.}\]

만약 클래스가 \(\omega_{1}, \omega_{2}, \dots\)인 Multiclass라면, 입력 데이터 \(\mathbf{x}\)에 대한 사후 확률이 가장 큰 클래스로 분류한다. 분류 규칙은 다음과 같다.

\[k = \text{arg}\max_{i}(P_{\omega_{i}} \mid \mathbf{x})\text{일 때 } \omega_{k} \text{로 분류하라.}\]

[!question] 그런데, 확률은 사건에 대해서만 계산 가능한 것 아닌가? \(\omega_{i}\)는 단순한 클래스 아닌가?{title} ‘데이터의 클래스가 \(\omega_{i}\)이다.’라는 사건으로 정의할 수 있다.

분류 문제의 실험은 무엇인가? 모집단에서 임의의 데이터를 하나 추출(sample)하고, 그 데이터의 특징 벡터 \(\mathbf{x}\)와 클래스 \(\omega\)를 관찰하는 행위와 같다. 이 실험의 표본 공간은 모든 가능한 \((\mathbf{x}, \omega)\) 쌍이다.

사건이 무엇인가? 표본 공간의 부분집합이다. 즉, 클래스 \(\omega_{i}\) 사건이란, 추출한 데이터의 클래스가 \(\omega_{i}\)인 모든 결과 집합이라고 볼 수 있다.

따라서 \(P(\omega_{i}\mid\mathbf{x})\)는, 사건 ‘데이터의 특징이 \(\mathbf{x}\)이다.’가 일어났다는 조건 하에 사건 ‘데이터의 클래스가 \(\omega_{i}\)이다’.가 일어날 확률이다.

사후 확률은 다음과 같다.

\[P(\omega_{i}\mid\mathbf{x}) = \frac{p(\mathbf{x} \mid \omega_{i})P(\omega_{i})}{p(\mathbf{x})}\]

데이터 \(\mathbf{x}\)가 연속적이라고 가정하고, 우도를 확률 밀도로 작성한다.

즉, 클래스 별 사전 확률 \(P(\omega_{i})\)와 우도 \(p(\mathbf{x}\mid\omega_{i})\)를 계산할 수 있으면, 사후 확률을 계산해 분류가 가능하다. 분모 \(p(\mathbf{x})\)는 무시해도 된다. \(P(\omega_{i}\mid\mathbf{x})\)를 비교하는데, 모두 공통분모로 들어있기 때문이다.

먼저 사전 확률은 단순히 클래스 \(\omega_{i}\)의 원소 \(n_{i}\)과 전체 데이터 개수 \(N\)으로 계산 가능하다.

\[P(\omega_{i}) = \frac{n_{i}}{N}\]

우도는 훈련 집합을 통해 \(p(\mathbf{x}\mid\omega_{i})\)를 추정해야 한다. 부류 조건부 확률이라고도 하며, 매우 중요한 문제다.

최소 위험 베이지안 분류기란?

최소 위험 베이지안 분류기란, 잘못 분류했을 때 위험도를 최소화한다. 최소 오류 베이지안 분류기와 무엇이 다를까? 잘못 분류했을 때 위험도가 다른 경우가 있다. 예를들어 환자인 사람을 정상으로 분류하는 것이 정상인 사람을 환자로 분류하는 것보다 더 위험하다. 이런 위험도에 가중치를 매기고, 그 위험도를 최소화하는 분류기가 최소 위험 베이지안 분류기다.

손실 행렬 \(C\)를 정의한다. 손실 행렬의 i행 j열의 값은, \(\omega_{i}\)로 분류해야 하는데 \(\omega_{j}\)로 잘못 분류했을 때 생기는 손실과 같다. \(i=j\)이면 \(c_{ij}\) 값은 0이 될 것이다. 그 이유는, 잘 분류했기 때문이다.

클래스 \(\omega_{i}\)를 선택했을 때 예상 손실도 \(q_{i}\)를 다음과 같이 계산할 수 있다.

\[q_{i} = \sum_{j}c_{ji} P(\omega_{j} \mid \mathbf{x})\]

만약 클래스가 \(\omega_{1}, \omega_{2}\) 두개일 때 최소 위험 베이지안 분류기의 분류 규칙은 다음과 같다.

\[\mathbf{x}\text{를 } q_{2} > q_{1} \text{이면 } \omega_{1} \text{로 분류하고, } q_{1} > q_{2} \text{면 } \omega_{2}\text{로 분류하라.}\]

우도비로 다시 쓰면, 다음과 같다.

\[\mathbf{x}\text{를 } \frac{p(\mathbf{x} \mid \omega_{1})}{p(\mathbf{x} \mid \omega_{2})} > T \text{이면 } \omega_{1} \text{로 분류하고, } \frac{p(\mathbf{x} \mid \omega_{1})}{p(\mathbf{x} \mid \omega_{2})} < T \text{면 } \omega_{2}\text{로 분류하라.}\]

이때, \(T\)의 정의는 다음과 같다.

\[T \equiv \frac{(c_{21} - c_{22}) P(\omega_{2})}{(c_{12} - c_{11})P(\omega_{1})}\]

이는 \(q_{1} = c_{11}p(\omega_{1}\mid\mathbf{x}) + c_{21}p(\omega_{2}\mid\mathbf{x})\), \(q_{2} = c_{12}p(\omega_{1}\mid\mathbf{x}) + c_{22}p(\omega_{2}\mid\mathbf{x})\)를 대입하면 쉽게 유도할 수 있다.

만약 클래스가 \(\omega_{1}, \omega_{2}, \dots\)인 Multiclass라면, \(q_{i}\) 값을 최소로 하는 클래스 \(\omega_{i}\)로 데이터 \(\mathbf{x}\)를 분류하면 된다. 분류 규칙은 다음과 같다.

\[\mathbf{x}\text{를 } k = \text{arg} \min_{i} q_{i}\text{일 때 } \omega_{k}\text{로 분류하라.}\]

식별 함수가 무엇인가?

베이지안 분류기를 식별 함수를 사용해서 분류 규칙을 일반화할 수 있다.

\[\mathbf{x}\text{를 } k = \text{arg} \max_{i} g_{i}(\mathbf{x})\text{일 때 } \omega_{k}\text{로 분류하라.}\]

식별 함수는 다음과 같다.

\[g_{i}(\mathbf{x}) = \begin{cases} P(\omega_{i}\mid\mathbf{x}) & \text{(최소 오류 베이지안 분류기)}\\ \frac{1}{q_{i}} & \text{(최소 위험 베이지안 분류기)} \end{cases}\]

왜 식별 함수를 쓰는가? 어차피 비교하는거면, \(f(x)\)가 단조 증가 함수라면 \(g_{i}(x)\)를 비교하는 것과 \(f(g_{i}(x))\)를 비교하는 것은 같은 효과를 낳는다. \(f(x)\)를 로그 함수로 택하면, 곱셈을 덧셈으로 바꿔주므로 수식 전개에 이점을 얻을 수 있다.

\[\ln(g_{i}(\mathbf{x})) = \ln(p(\mathbf{x}\mid\omega_{i})P(\omega_{i}))\] \[= \ln p(\mathbf{x}\mid\omega_{i}) + \ln P(\omega_{i})\]

또한 곱셈을 덧셈으로 바꾸면, 곱셈으로 생기는 매우 작은 언더플로우를 방지해 더 안정적인 값을 다룰 수 있다.

정규분포에서의 베이지안 분류기가 무엇인가?

정규 분포는 현실 세계와 잘 맞는 경향이 있다. 우도가 정규 분포를 따른다고 가정하고, 베이지안 분류기를 분석해보자. 기존의 정규 분포 식은 다음과 같다.

\[N(\mu,\sigma^2) = \frac{1}{(2\pi)^{1 / 2} \sigma} e^{- \frac{(x - \mu)^2}{2 \sigma^2}}\]

이를 평균벡터, 공분산행렬로 확장하면 다음과 같다.

\[N(\mathbf{\mu, \Sigma}) = \frac{1}{(2\pi)^{d/2} \lvert \Sigma \rvert^{1/2} } e^{- \frac{1}{2}(\mathbf{x} - \mathbf{\mu})^T \Sigma^{-1} (\mathbf{x} - \mathbf{\mu})}\]

이를 사용해 우도를 표현하자.

\[p(\mathbf{x}\mid\omega_{i}) = N(\mu_{i}, \Sigma_{i}) = \frac{1}{(2\pi)^{d/2} \lvert \Sigma_{i} \rvert^{1/2} } e^{- \frac{1}{2}(\mathbf{x} - \mathbf{\mu_{i}})^T \Sigma_{i}^{-1} (\mathbf{x} - \mathbf{\mu_{i}})}\]

로그를 씌워 식별 함수를 만들자.

\[g_{i}(\mathbf{x}) = \ln(p(\mathbf{x}\mid \omega_{i}) P(\omega_{i}))\] \[= \ln p(\mathbf{x} \mid \omega_{i}) + \ln P(\omega_{i})\] \[= \ln\left( \frac{1}{(2\pi)^{d/2} \lvert \Sigma_{i} \rvert^{1/2} } e^{- \frac{1}{2}(\mathbf{x} - \mathbf{\mu_{i}})^T \Sigma_{i}^{-1} (\mathbf{x} - \mathbf{\mu_{i}})} \right) + \ln P(\omega_{i})\] \[= \ln \frac{1}{(2\pi)^{d/2} \lvert \Sigma_{i} \rvert^{1/2} } + \ln e^{- \frac{1}{2}(\mathbf{x} - \mathbf{\mu_{i}})^T \Sigma_{i}^{-1} (\mathbf{x} - \mathbf{\mu_{i}})} + \ln P(\omega_{i})\] \[= \ln (2\pi)^{-d / 2} + \ln \lvert \Sigma_{i} \rvert^{ - 1/ 2 } + - \frac{1}{2}(\mathbf{x} - \mu_{i})^T \Sigma_{i}^{-1} (\mathbf{x}-\mu_{i}) + \ln P(\omega_{i})\] \[= - \frac{d}{2} \ln(2\pi) - \frac{1}{2} \ln \lvert \Sigma_{i} \rvert + \ln P(\omega_{i}) - \frac{1}{2} (\mathbf{x} - \mu_{i})^T \Sigma_{i}^{-1} (\mathbf{x} - \mu_{i})\]

이것이 식별 함수다. 더 풀어보면, 결론을 얻는다.

\[= - \frac{d}{2} \ln(2\pi) - \frac{1}{2} \ln \lvert \Sigma_{i} \rvert + \ln P(\omega_{i}) - \frac{1}{2} (\mathbf{x}^T\Sigma_{i}^{-1} - \mu_{i}^T\Sigma_{i}^{-1}) (\mathbf{x} - \mu_{i})\] \[= - \frac{d}{2} \ln(2\pi) - \frac{1}{2} \ln \lvert \Sigma_{i} \rvert + \ln P(\omega_{i}) - \frac{1}{2} (\mathbf{x}^T\Sigma_{i}^{-1}\mathbf{x} - \mathbf{x^T} \Sigma_{i}^{-1} \mu_{i} - \mu_{i}^T \Sigma_{i}^{-1} \mathbf{x} + \mu_{i}^T \Sigma_{i}^{-1} \mu_{i})\]

이때, \(\mathbf{x}^T \Sigma_{i}^{-1} \mu_{i}\)는 스칼라 값과 같고, 스칼라의 전치는 스칼라와 같다. 그리고, 공분산 행렬은 대칭행렬이다. 따라서

\[\mu_{i}^T \Sigma_{i}^{-1} \mathbf{x} = (\mu_{i}^T \Sigma_{i}^{-1} \mathbf{x})^T = \mathbf{x}^T \Sigma_{i}^{-1} \mu_{i}\]

즉 다음과 같다.

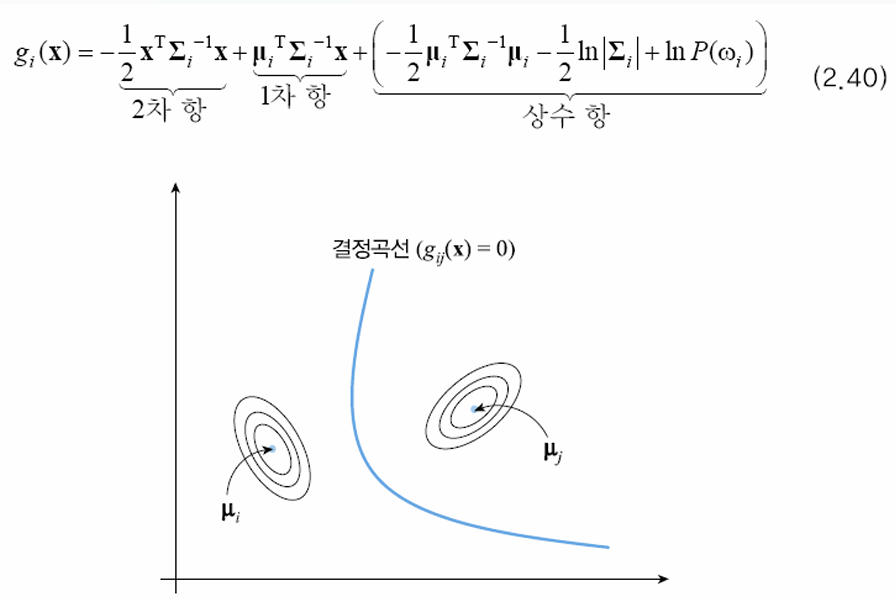
\[g_{i}(\mathbf{x}) = - \frac{1}{2} (\mathbf{x}^T\Sigma_{i}^{-1}\mathbf{x}- 2\mu_{i}^T \Sigma_{i}^{-1} \mathbf{x} + \mu_{i}^T \Sigma_{i}^{-1} \mu_{i})- \frac{d}{2} \ln(2\pi) - \frac{1}{2} \ln \lvert \Sigma_{i} \rvert + \ln P(\omega_{i})\]

\(g_{i}(\mathbf{x})\)는 \(\mathbf{x}\)에 대한 2차식이다.

베이지안 분류기에서 학습하는 방법은, 주어진 데이터를 통해 각 클래스 별 \(\mu_{i}\), \(\Sigma_{i}\)를 미리 계산해두는 것이다. 그러면 \(\mathbf{x}\)가 주어지면 식별 함수 \(g_{i}(\mathbf{x})\)를 구할 수 있고, 이를 통해 분류가 가능하다.

[!tip] 역행렬{title}

\[M_{ij}^{-1} = \frac{1}{\det M} cof(M_{ji})\] \[cof(M_{ij}) = (-1)^{i+j}\det M_{ij}^C\]

\(M_{ij}^C\)는 \(M\)에서 \((i,j)\)를 포함한 행, 열을 제외한 행렬과 같다.

\(2\times 2\) 역행렬:

\[A^{-1} = \frac{1}{ad - bc} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}\]

대각행렬 역행렬: 대각선의 역수

결정 경계가 무엇인가?

두 클래스 \(\omega_{i}\), \(\omega_{j}\)를 구분하는 경계는, 다음 조건을 만족하는 \(\mathbf{x}\)와 같다.

\[g_{i}(\mathbf{x}) = g_{j}(\mathbf{x})\]

즉, 다음을 만족하는 \(\mathbf{x}\)의 집합과 같다.

\[g_{ij}(\mathbf{x}) = g_{i}(\mathbf{x}) - g_{j}(\mathbf{x}) = 0\]

선형 분류가 무엇인가?

정규분포를 따르는 베이지안 분류기가 모든 부류의 공분산 행렬이 같은 상황과 같다.

\[\Sigma_{i} = \Sigma\]

식별 함수를 \(i\) 항이 있는 것과, 없는 것으로 구분하면 다음과 같다.

\[g_{i}(\mathbf{x}) = \frac{1}{2}\underbrace{(\mu_{i}^T \Sigma_{i}^{-1} \mu_{i}- 2\mu_{i}^T \Sigma_{i}^{-1} \mathbf{x} + 2 \ln P(\omega_{i}))}_{\text{i에 따라 다름}} - \frac{1}{2} \underbrace {(\mathbf{x}^T\Sigma_{i}^{-1}\mathbf{x} - d\ln 2\pi + \ln \lvert \Sigma \rvert )}_{\text{i에 무관함}}\]

\(i\)에 무관한 항은 지워도 되므로, \(\mathbf{x}\)에 대한 선형식으로 변한다.

\[g_{i}(\mathbf{x}) = (\Sigma^{-1} \mu_{i})^T \mathbf{x} + \left( \ln P(\omega_{i}) - \frac{1}{2} \mu_{i}^T \Sigma^{-1} \mu_{i} \right)\] \[= \mathbf{w}_{i}^T \mathbf{x} + b_{i}\]

선형 분류의 결정 경계는 다음과 같다.

선형 분류의 결정 경계계는 직선이다.

비선형 분류란 무엇인가?

비선형 분류의 결정 경계는 비선형이다.

기각이란 무엇인가?

만약 정상일 확률 55%, 암일 확률 45%와 같이 암인지 아닌지 애매한 경우는 판단을 보류해야 한다. 즉, 판단을 기각해야 한다.

\[\lvert P(\omega_{1} \mid \mathbf{x}) - P(\omega_{2} \mid \mathbf{x}) \rvert < \Delta\]

이면 판단을 기각한다. \(\Delta\)는 사용자가 설정하는 임계값이다. 이 값이 클수록, 분류기가 더 확실한 상황에서만 분류한다.