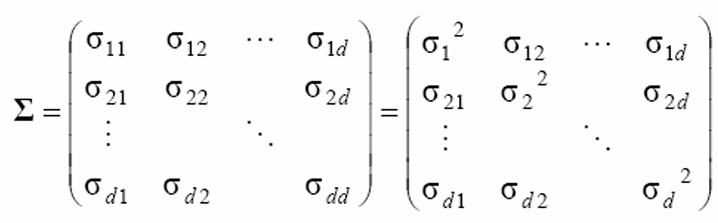인공지능 11. 불확실한 정보를 다루는 방법
불확실한 정보를 기반으로 어떻게 추론하는가?
결국 목표는 추론 가능한 에이전트를 만드는 것이다. 지금 지식 베이스는 결정론적 지식, 비결정론적 지식을 구축할 수 있게 되었다. 결정론적 지식은 그냥 추론 사슬을 통해 추론하면 된다. 주관적인 지식은 퍼지 추론을 사용한다. 그렇다면, 불확실한 지식을 가지고 어떻게 추론을 통해 새로운 지식을 얻어낼까?
불확실한 정보란, 다음과 같은 정보다.
\[\text{내일 비가 올 수도 있고 안올 수도 있다.}\]이런 불확실한 정보를 나타내기 위해 확률을 도입한다.
\[\text{내일 비가 67\% 확률로 온다.}\]현재 가장 많이 사용하는 방법은 확률론(Probability Theory)을 도입하고, 베이지안 추론(Bayesian Inference)을 사용하는 것이다.
확률론이 무엇인가?
실험(Experiment)이란, 어떤 현상을 관찰하는 행위다. 동전 던지기, 주사위 굴리기 표본 공간(Sample Space)이란, 실험에서 일어날 수 있는 모든 가능한 결과들의 집합이다. 예를들어 주사위를 던질 때 표본공간 \(S\)는 다음과 같다.
사건(Event)이란, 표본 공간의 부분집합이다. 우리가 관심을 갖는 특정 결과들의 집합이다. 예를들어 짝수가 나오는 사건은 다음과 같다.
\[E = \{ 2,4,6 \}\]확률(Probability)이란, 실험을 통해 특정 사건 \(E\)가 일어날 가능성을 0과 1 사이의 숫자로 표현한 것이다.
\[P(E) = \frac{\text{사건 E의 원소 개수}}{\text{표본 공간 S의 원소 개수}}= \frac{3}{6} = 0.5\]확률을 사용하면 불확실한 실험 결과를 숫자로 표현할 수 있다.
확률 변수가 무엇인가?
표본 공간 내의 수학적 대상은 항상 숫자가 아닐 수 있다. 예를들어, 동전 던지기의 표본 공간은 다음과 같다.
\[\Omega=\{ H,T\}\]이러한 경우를 쉽게 다루려면, 표본 공간에 있는 각각의 결과를 실수 값에 대응시키는 함수가 필요하다. 이 함수를 확률 변수(Random Variable)라 한다.
예를들어, 동전 두개 던지기를 예로 들면, 표본 공간은 다음과 같다.
\[\Omega = \{ (H,H), (H,T), (T,H), (T,T) \}\]확률 변수 \(X(s)\), \(^\forall s \in S\)를 앞면이 나온 횟수라 정의하자. 매핑하면 다음과 같다.
\[X((H,H)) = 2, ~~X((H,T))= 1, ~~X((T,H)) = 1,~~ X((T,T)) = 0\]앞으로 이 확률 변수 \(X\)가 이산적인지, 연속적인지 두가지 경우를 생각해야 한다.
확률 변수 \(X\)의 새로운 표본 공간은 다음과 같이 표기한다.
\[\Omega_{X} = \{ 0, 1, 2 \}\]위 표본 공간은 근원 표본 공간과 다르다. 근원 표본 공간은 실험 결과의 모든 가짓수이며, 확률 변수의 표본 공간은 확률 변수의 값 공간 또는 치역(Range) 이다.
확률 분포가 무엇인가?
먼저 \(X\)가 이산적인 경우를 따져보자. 사건을 확률변수로 표현할 수 있게 되었다. 확률 변수가 \(X=x_{0}\)일 사건, 확률 변수가 \(X=x_{1},x_{2},\dots\)일 사건 등.
동전 두개 던지기 예제에서 확률 변수가 \(1\)일 사건은 앞면과 뒷면이 동시에 나온 사건과 동치이며, 그 확률은 다음과 같다.
\[P(X=1) = \frac{2}{4} = \frac{1}{2}\]각각의 확률 변수 \(^\forall x \in X\)에 대응하는 확률 \(P(X=x)\)를 짝지어 둔 목록 또는 함수를 확률 분포(Probability Distribution)라고 한다. 이산적 확률 분포는 확률 질량 함수 \(P(X=x)\), 표, 막대 그래프 등으로 나타낼 수 있다. 연속적 확률 분포는 확률 밀도 함수 \(f(x)\), 그래프로 나타낼 수 있다. 확률 변수가 \([a, b]\) 범위일 확률은 다음과 같이 계산한다.
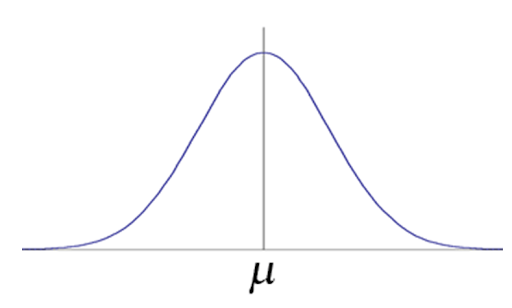
\[P(a \leq x \leq b) = \int_{a}^{b} f(x)dx\]일상에서 가장 많이 사용되는 확률 밀도 함수는 정규 분포 또는 가우시안 함수이며, 그 모양과 식은 다음과 같다.
\[f(x) = \frac{1}{\sigma \sqrt{ 2\pi }} e^{-(x - \mu)^2 / 2 \sigma^2}\]그리고, 총 확률의 합은 1이어야 한다.
\[\sum_{i}P(X=x_{i}) = 1\] \[\int_{-\infty}^{\infty} f(x)dx = 1\]결합 확률이 무엇인가?
\[Z=(X,Y)\]2개 이상의 확률 변수를 한 쌍으로 묶어서 결합 확률 변수(Joint Random Variable)로 생각할 수 있다. 결합 확률 변수는 벡터다. \(Z\)의 표본 공간은, 각각의 확률 변수의 표본 공간의 곱으로 정의된다. 확률 변수가 \(\{X_{1}, X_{2}, \dots, X_{n} \}\)에 대한 결합 표본 공간은 다음과 같다.
\[\Omega_{X_{1}} \times \Omega_{X_{2}} \times \dots \times \Omega_{X_{n}} = \prod_{i=1} \Omega_{X_{i}}\]결합 확률 변수에 대응하는 확률의 분포가 결합 확률 분포(Joint Probability Distribution)이다. 이는 표, 그래프로 나타낼 수 있다.
예를들어, 색깔이 다른 두 동전을 동시에 던질 때는 첫번째 동전이 앞면인 경우를 \(X\), 두번째 동전이 앞면인 경우를 \(Y\)라고 하자. 그때의 이산 결합 확률 분포표는 다음과 같다.
연산 결합 확률 분포는 결합 확률 밀도 함수 \(f(x,y)\)로 표현되며, \(X\)가 \([a,b]\) 범위일 확률인 동시에 \(Y\)가 \([c,d]\)일 확률은 이중적분으로 계산된다.
\[P(a \leq X \leq b, c \leq Y \leq d) = \int_{c}^{d}\int_{a}^{b} f(x,y) dx dy\]결합 확률 분포를 알면, 각 개별 확률 변수의 확률 분포를 얻어낼 수 있다. 이를 주변 확률 분포라고 한다. 아이디어는 \(X=x\)에 대응되는 나머지 확률 변수의 값을 모두 더하는 것이다.
\[P(X=x) = \sum_{y} P(X=x, Y=y)\] \[f(x) = \int_{-\infty}^{\infty}f(x,y)dy\]만약 다음 조건을 만족하면, 두 확률 변수 \(X, Y\)는 독립이라고 정의한다.
\[P(X,Y) = P(X) P(Y)\]조건부 확률이 무엇인가?
조건부 확률 개념에는 두개의 사건이 존재한다. 사건 \(B\)가 일어났다는 조건 하에 사건 \(A\)가 일어날 확률을 조건부 확률이라 한다.
\[P(A\midB) = \frac{P(A \cap B)}{P(B)}\]표본 공간을 사건 \(B\)의 집합으로 가정하고, 사건 \(A\)와 \(B\)의 부분집합이 일어날 확률이 바로 사건 \(B\)가 일어났다는 조건 하에 사건 \(A\)가 일어날 확률과 동일하다.
예를들어, 주사위를 던졌을 때 짝수가 나왔다는 조건 하에 3보다 큰 수가 나오는 조건부 확률을 계산해보자. 표본 공간은 다음과 같다.
\[S = \{ 1,2,3,4,5,6\}\]3보다 큰 수가 나오는 사건 \(A\)는 다음과 같다.
\[A = \{ 4,5,6 \}\]짝수가 나오는 사건 \(B\)는 다음과 같다.
\[B = \{ 2, 4, 6 \}\]사건 \(A\)와 \(B\)의 교집합은 다음과 같다.
\[A \cap B = \{ 4, 6 \}\]교집합 사건의 확률과 \(B\) 사건의 확률은 다음과 같다.
\[P(A \cap B) = \frac{2}{6} = \frac{1}{3}, ~~P(B) = \frac{3}{6} = \frac{1}{2}\]따라서, 사건 \(B\)가 발생한 조건 하에 \(A\)가 발생할 조건부 확률은 다음과 같다.
\[P(A\midB) = \frac{\frac{1}{3}}{\frac{1}{2}} = \frac{2}{3}\]베이스가 무엇인가?
베이스 정리를 알게 되면, 베이지안 추론을 할 수 있게 된다. 베이지안 추론이 무엇인가? 베이지 추론의 목적은, 증거들을 종합하여 어떤 가설이 얼만큼 정확한지 그 확률을 추론하는 것이다.
어떤 가설 \(H\)를 설정하고, 증거 \(E\)들을 종합해봤을 때 최종적으로 그 가설 \(H\)가 얼마나 정확한지 추론해낼 수 있다.
이때 가설 \(H\)가 보편적으로 사실일 확률을 \(P(H)\)라고 하며, 이를 사전 확률이라 한다. 이는 미리 알고이는 정보와 같다. 어떤 가설 \(H\)가 사실이라고 가정했을 때, 우리가 관찰한 증거 \(E\)가 나타날 조건부 확률을 \(P(E\midH)\)라고 하며, 이를 우도라고 한다. 증거 \(E\)를 관찰한 후에, 가설 \(H\)가 사실일 것이라고 업데이트되는 확률을 \(P(H\midE)\)라고 하며, 이를 사후 확률이라고 한다. 사후 확률을 계산하는 계산식이 베이스 정리다.
\[\underbrace{P(H\midE)}_{\text{사후 확률}} = \frac{\overbrace{P(E\midH)}^{\text{우도}} \cdot \overbrace{P(H)}^{\text{사전 확률}}}{\underbrace{P(E)}_{\text{증거 확률}}}\]예를 들어, 어떤 환자가 기침을 하며 본인이 폐럼인지 아닌지 검사하러 온 상황을 생각해보자. 가설 \(H\)는 ‘이 환자가 폐렴에 걸렸다.’로 설정한다. 전체 인구 중 폐렴에 걸린 사람은 0.1%정도이므로, 사전 확률은 다음과 같다.
\[P(H) = 0.001\]폐렴인 환자가 기침을 할 확률을 \(80\%\)라 하자. 따라서 우도는 다음과 같다.
\[P(E\midH) = 0.8\]보편적인 일반인이 기침할 확률이 증거 확률이며, 이를 \(10\%\)라고 가정하자.
\[P(E) = 0.1\]이를 통해 사후 확률 \(P(H\midE)\)를 베이스 정리를 통해 계산해낼 수 있다.
\[P(H\midE) = \frac{0.8 \times 0.001}{0.1} = 0.008\]즉, 기침하는 환자가 폐렴일 확률은 \(0.8\%\)라고 추론해낼 수 있다.
평균 벡터, 공분산 행렬이 무엇인가?
하나의 관측 대상에 대한 여러개의 수치적 특징(feature)를 모아둔 벡터 \(\mathbf{x}\)를 특징 벡터 (Feature Vector)라고 하자. 이는 각각의 확률 변수 \(\{X_{1}, X_{2}, \dots, X_{n}\}\)을 벡터 \(\mathbf{x}\)로 묶은 것과 같다.
이산적인 확률 변수를 다루고, \(\mathbf{x}\)에 대응하는 확률 질량 함수 \(P(\mathbf{x})\)를 정확히 알고 있다면 평균 벡터 \(\mathbf{\mu}\)와 공분산 행렬 \(\Sigma\)은 다음과 같다.
\[\mathbf{\mu} = \sum_{\mathbf{x}} \mathbf{x}P(\mathbf{x})\] \[\Sigma = \sum_{\mathbf{x}} (\mathbf{x} - \mathbf{\mu})(\mathbf{x} - \mathbf{\mu})^T P(\mathbf{x})\]연속적인 확률 변수를 다루고, \(\mathbf{x}\)에 대응하는 확률 밀도 함수 \(p(\mathbf{x})\)를 정확히 알고 있다면 평균 벡터 \(\mathbf{\mu}\)와 공분산 행렬 \(\Sigma\)은 다음과 같다.
\[\mathbf{\mu} = \int_{R^d} \mathbf{x} p(\mathbf{x}) d\mathbf{x}\] \[\Sigma = \int_{R^d} (\mathbf{x} - \mathbf{\mu}) (\mathbf{x} - \mathbf{\mu})^T p(\mathbf{x})d \mathbf{x}\]그러나 위와 같은 이상적인 상황은 거의 없고, 보통 Sample Data를 추출해서, 그 Sample Data의 평균과 공분산 행렬을 구하는 경우가 많다. Sample Data가 \(\mathbf{x}_{1}, \mathbf{x}_{2}, \dots, \mathbf{x}_{N}\)와 같이 주어진다면 평균 벡터 \(\mathbf{\mu}\)와 공분산 행렬 \(\Sigma\)은 다음과 같다.
\[\mathbf{\mu} = \frac{1}{N} \sum_{i=1}^{N} \mathbf{x}_{i}\] \[\Sigma = \frac{1}{N-1} \sum_{i=1}^{N} (\mathbf{x_{i} - \mathbf{\mu}})(\mathbf{x}_{i} - \mathbf{\mu})^T\]공분산 행렬은 아래와 같이 생겼다.
대각 성분은 각 확률 변수의 분산이며, 크로스 성분은 두 확률 변수의 상관관계와 같다.
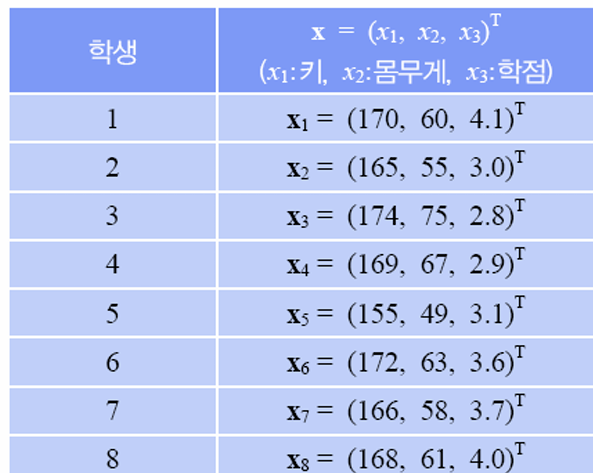
8개의 샘플이 주어졌을 때, 평균 벡터와 공분산 행렬은 다음과 같다.
키와 몸무게는 상관관계가 꽤 있지만, 학점과 키, 몸무게는 상관관계가 거의 없음을 확인할 수 있다.
보통 차원의 크기 (Feature 개수) \(d\)를 늘릴 수록 추론이 정확해진다. 그러나 표본 공간이 커진다. 표본 공간이 커지면 Search가 힘들어진다. 따라서, 핵심 Feature만 추출해서 모델링하는게 중요하다. 그렇기 위해선, 상관 관계가 높은 두 Feature는 하나로 줄이는게 낫다. 위 예제에서 키와 몸무게는 상관관계가 크므로, 둘 중 하나만 사용해도 무방하다.
Gaussian Mixture Model
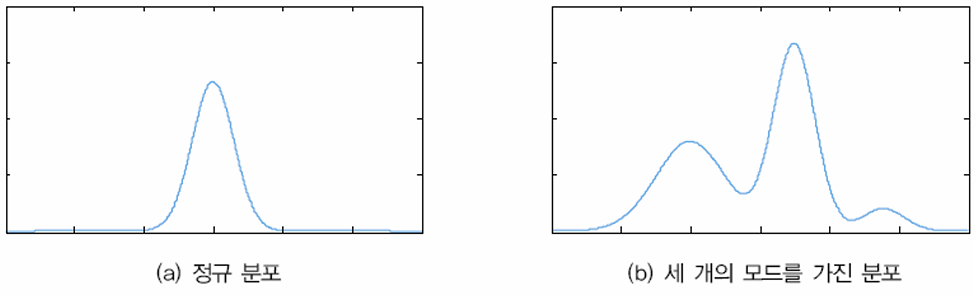
어떤 확률 분포 \(X\)가 단일 가우시안 분포를 따를 수 있지만, 모드가 여러개 존재할 수도 있다. 그럴땐 이를 뭉뚱그려 하나의 가우시안으로 생각하지 말고, 가우시안 분포가 여러개 결합되어있는 모양으로 생각하는게 합리적이다.
만약 세개의 모드가 있다면, 확률 분포는 세개의 가우시안 분포가 결합된 모양과 같다.
\[N_{1} \sim (\mu_{1}, \sigma_{1}), ~~N_{2} \sim (\mu_{2}, \sigma_{2}),~~N_{3} \sim (\mu_{3}, \sigma_{3}),\]따라서 확률 밀도 함수는 다음과 같을 것이다.
\[P(X) = \alpha_{1} N_{1} + \alpha_{2}N_{2} + \alpha_{3}N_{3}\]\(\alpha_{i}\) 파라미터를 찾아내는 알고리즘 (EM 알고리즘)을 대학원 과정에서 배운다고 한다.