인공지능 10. 주관적인 지식을 다루는 방법

애매한(Fuzzy) 지식을 어떻게 모델링할까?

Fuzzy란, 모호한 지식을 명확하게 다루기 위한 수리 이론이다. 모호한 지식이란, ‘저 여자는 예쁘다’와 같이 참/거짓으로 구분하기 어려운 지식을 말한다. 따라서 Fuzzy Theory에선 가중치를 사용한다. 어떤 여자는 0.6만큼 예쁘다, 어떤 여자는 0.4만큼 예쁘다와 같이 주관적인 지식을 표현한다.

집합을 도입한다. 결정론적 논리에선 원소가 특정 집합에 속하는 경우는 속하거나(1)/속하지 않거나(0) 둘 중 하나로 구분할 수 있다. 그러나, 비결정론적 논리에선 원소가 특정 집합에 속하는 정도를 \([0, 1]\) 사이의 범위로 나타낸다. 그 집합이 Fuzzy Set이고, 특정 집합 \(A\)에 속하는 소속도를 반환하는 함수를 Membership Function (소속 함수) 라고 한다.

\[\mu_{A}(x) : X \to [0, 1]\]

이 소속 함수는 마치 휴리스틱 함수처럼 잘 정의해야 한다.

[!NOTE] 퍼지 이론의 언어로 위 예제를 표현하면?{title} 어떤 여자 \(^\exists A\)는 ‘예쁘다’ 퍼지 집합에 속하는 정도는 \(\mu_{\text{예쁘다}}(A)\)와 같다.

퍼지 집합의 연산이 무엇인가?

만약 키가 크고(AND) 잘생긴 사람의 소속도는? 키가 크지 않은(NOT) 사람의 소속도는? 키가 크거나(OR) 돈이 많은 사람의 소속도는? 어떻게 계산할 수 있을까?

집합을 각각 교집합(AND), 합집합(OR), 여집합(NOT)로 생각하고, 그 집합의 소속 함수를 정의한다. 임의의 원소 Set \(^\forall x \in X\)와 두 개의 퍼지 집합 \(A,B\)를 가정하자. (1) 여집합

\[\mu_{A^c}(x) = 1-\mu_{A}(x)\]

예를들어, \(A\)가 ‘젊다’의 퍼지 집합이라면, 그것의 여집합은 ‘젊지 않다’와 같다.

(2) 합집합

\[\mu_{A\cup B}(x) = \max(\mu_{A}(x), \mu_{B}(x))\]

(3) 교집합

\[\mu_{A \cap B} (x) = \min(\mu_{A}(x), \mu_{B}(x))\]

여집합은 납득이 간다. 교집합, 합집합은 왜 \(min, max\)를 사용하는걸까?

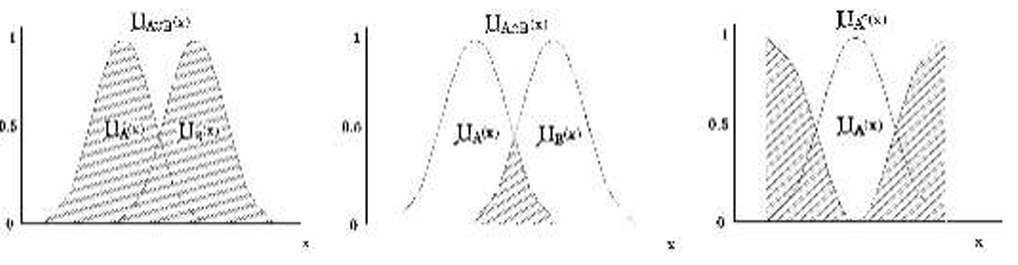
위 그래프의 \(x\)축은 \(x\), \(y\)축은 소속함수 값을 그린 것이다. 첫번째 그림은 합집합이다. 합집합의 소속함수 값은, 두 소속함수 중 큰 값을 취한 것과 같다. 두번째 그림은 교집합이다. 교집합의 소속함수 값은, 두 소속함수 중 작은 값을 취한 것과 같다.

퍼지 관계가 무엇인가?

관계 Relation란 무엇인가? 두 집합 \(X, Y\)가 있을 때 관계 \(R\)은 순서쌍 \((x,y)\)의 집합으로 정의한다. 어떤 순서쌍 \((x,y)\)는 관계 \(R\)에 속하거나, 속하지 않거나 둘 중 하나와 같다.

퍼지 관계 Puzzy Relation란 무엇인가? 두 집합 \(X,Y\)가 있을 때 퍼지 관계 \(R\)은 순서쌍 \((x,y)\)가 \(R\)가 어느 정도로 속하는지를 나타낸다. 퍼지 관계는 다음 소속 함수로 정의한다.

\[\mu_{R}(x,y): X \times Y \to [0, 1]\]

이 퍼지 관계의 소속 함수 또한 휴리스틱처럼 잘 정의해야 한다.

예를들어 사람들 \(X = \{ 철수, 영희 \}\)와 과일들 \(Y = \{사과, 배, 포도 \}\)을 정의하자. 관계 \(R\)을 ‘좋아한다’로 정의하자. 철수는 사과는 0.5만큼 좋아하고, 배를 0.3만큼 좋아하고, 포도를 0.7만큼 좋아한다. 영희는 또 각각 좋아하는 정도가 다를 것이다. 이러한 관계 \(R\)를 행렬로 한번에 표현할 수 있다. 행을 \(X\), 열을 \(Y\)의 원소라고 하자.

\[R = \begin{pmatrix} 0.5 & 0.3 & 0.7 \\ 0.9 & 0.6 & 0.2 \end{pmatrix}\]

즉, \(X=\{ x_{1}, x_{2}, \dots, x_{n} \}, Y= \{ y_{1}, y_{2}, \dots, y_{n} \}\)라고 하면 관계 \(R\)은 다음과 같다.

\[R = \begin{pmatrix} \mu_{R}(x_{1},y_{1}) & \mu_{R}(x_{1}, y_{2}) & \dots & \mu_{R}(x_{1},y_{m}) \\ \mu_{R}(x_{2},y_{1}) & \mu_{R}(x_{2}, y_{2}) & \dots & \mu_{R}(x_{2}, y_{m}) \\ \vdots & \vdots & & \vdots\\ \mu_{R}(x_{n}, y_{1}) & \mu_{R}(x_{n}, y_{2}) & \dots & \mu_{R}(x_{n}, y_{m}) \end{pmatrix}\]

역퍼지 관계가 무엇인가?

퍼지 관계 \(R:X \to Y\)라면, 역퍼지 관계는 \(R^{-1}: Y \to X\)다. 즉, 사람이 과일을 좋아하는 정도였다면 역퍼지 관계는 과일이 사람에게 사랑받는 정도와 같다.

\[\mu_{R^{-1}}(y,x): Y \times X \to [0, 1]\]

이는 그저 역행렬과 같다.

\[R^{-1} = R^{T} = \begin{pmatrix} \mu_{R^{-1}}(y_{1},x_{1}) & \mu_{R^{-1}}(y_{1}, x_{2}) & \dots & \mu_{R^{-1}}(y_{1},x_{n}) \\ \mu_{R^{-1}}(y_{2},x_{1}) & \mu_{R^{-1}}(y_{2}, x_{2}) & \dots & \mu_{R^{-1}}(y_{2}, x_{n}) \\ \vdots & \vdots & & \vdots\\ \mu_{R^{-1}}(y_{m}, x_{1}) & \mu_{R^{-1}}(y_{m}, x_{2}) & \dots & \mu_{R^{-1}}(y_{m}, x_{n}) \end{pmatrix}\]

즉 위 철수, 영희 예제의 역퍼지 관계는 다음과 같다.

\[R^{-1} = R^{T} = \begin{pmatrix} 0.5 & 0.9 \\ 0.3 & 0.6 \\ 0.7 & 0.2 \end{pmatrix}\]

[!example] example{title}

퍼지 관계 \(R\)의 소속 함수를 다음과 같이 정의하자.

\[\mu_{R}(x,y) = \begin{cases} 0 & \text{if } x \geq y \\ \frac{y-x}{\max(Y)- \min(X)} & \text{if } x < y \end{cases}\]

퍼지 관계 \(R\)는 다음과 같다.

\[R = \begin{pmatrix} 0 & \frac{1}{2} & 1 \\ 0 & \frac{1}{4} & \frac{3}{4} \end{pmatrix}\]

역퍼지 관계 \(R^{-1}\)은 다음과 같다.

\[R^{-1} = \begin{pmatrix} 0 & 0 \\ \frac{1}{2} & \frac{1}{4} \\ 1 & \frac{3}{4} \end{pmatrix}\]

퍼지 관계의 연산이 무엇인가?

퍼지 관계 집합도 퍼지 집합의 일종이다. 따라서, 합집합 교집합 여집합 연산을 그대로 사용할 수 있다. 임의의 원소 Set \(^\forall (x,y) \in X \times Y\)와 두 개의 퍼지 관계 \(P,R\)를 가정하자. (1) 여집합

\[\mu_{P^c}(x,y) = 1-\mu_{P}(x,y)\]

(2) 합집합

\[\mu_{P\cup R}(x,y) = \max(\mu_{P}(x,y), \mu_{R}(x,y))\]

(3) 교집합

\[\mu_{P \cap R} (x,y) = \min(\mu_{P}(x,y), \mu_{R}(x,y))\]

예를들어 \(P\)를 좋아한다, \(R\)을 친하다라고 하자. \(P^c\)는 좋아하지 않는 관계다. \(P \cup R\)은 좋아하거나 친한 관계다. \(P \cap R\)은 좋아하고 친한 관계다.

퍼지 관계의 합성이 무엇인가?

관계를 합성한다는게 무슨 말일까? 두 관계 \(P: X \to Y\), \(R : X \to Z\)를 생각해보자. 두 관계의 합성 관계는 \(P \circ R : X \to Z\)와 같다. 즉, 두 관계를 통해서 새로운 관계를 추론해내는 것과 같다.

새로운 퍼지 관계 집합 \(^\exists(x,z) \in X \times Z\)의 원소가 존재하려면? 적어도 하나의 \(X\to Y\) 관계가 \(^\exists(x,y) \in X \times Y\)에 존재해야 하며, 동시에 적어도 하나의 \(Y \to Z\) 관계가 \(^\exists(y,z) \in Y \times Z\)에 존재해야 \(X \to Z\) 관계가 적어도 하나 존재해야 한다.

이를 논리식으로 쓰면 다음과 같다. 고전 관계이므로 \(\mu_{P}, \mu_{R}\)는 0 또는 1의 값을 가진다.

\[\mu_{P \circ R}(x,z) = (\mu_{P}(x,y_{1}) \land \mu_{R}(y_{1},z) ) \lor (\mu_{P}(x,y_{2}) \land \mu_{R}(y_{2},z) ) \lor \dots\]

그렇다면, 퍼지 관계를 합성한다는 것은 무슨 말일까? 퍼지 관계의 합성 또한 두 퍼지 관계를 통해서 새로운 관계를 추론하는 것과 같다. 두 퍼지 관계를 합성했을 때 나오는 새로운 퍼지 관계 집합 \(P \circ R :X \times Z\)의 소속 함수는 \(\lor \to \max\), \(\land \to \min\)으로 자연스럽게 확장할 수 있다.

\[\mu_{P \circ R}(x,z) = \max_{y \in Y} [\min\{\mu_{P}(x,y), \mu_{R}(y,z)\}]\]

두 관계 \(P, R\)가 행렬로 주어지면, 합성을 통해 얻는 새로운 관계 \(T\)는 두 행렬을 마치 행렬곱 하듯 계산하면 된다.

그러나 \(*\) 연산이 \(\min\), \(+\) 연산이 \(\max\)가 되는 것 뿐이다.

\[T_{11} = \max[\min(P_{11}, R_{11}), \min(P_{12}, R_{21}), \min(P_{13}, R_{31})]\] \[= \max(0, 0.3, 0.5) = 0.5\]

퍼지 논리가 무엇인가?

기존의 논리식에서 사용되는 연산자는 다음과 같다.

\[\land = \text{AND}, ~~\lor = \text{OR}, ~~\lnot = \text{NOT}, ~~\to = \text{조건}, ~~ \leftrightarrow = \text{동치}\]

이때 \(P, Q\)는 참(1) 또는 거짓(0)의 값만 가질 수 있었다. 이를 \([0,1]\) 범위로 확장한 규칙을 퍼지 논리라고 한다. 따라서 연산자 또한 퍼지 규칙에 맞게 변형된다.

\[\min = \text{AND}, ~~\max = \text{OR}, ~~1-a = \text{NOT}, \to = \min(1, 1-a+b)\]

조건 명제가 왜 위와 같이 정의되는가? 앞서 \(P\to Q\)는 \(\lnot P \lor Q\)와 동치라고 했다. 따라서 \(\max(1-a, b)\)와 같아야 하는 것 아닌가? 맞다. 그렇게 쓸 수도 있다. 그러나 제시된 정의가 퍼지 추론 시스템에서 더 강력한 수학적 기반을 제공하며, 특히 퍼지 제어 시스템에서 널리 사용된다고 한다.

퍼지 규칙이 무엇인가?

정리해보자. 퍼지 이론에서의 사실은 퍼지 집합과 소속 함수와 같다. 규칙은 퍼지 규칙과 같다. 지식은 사실 + 규칙과 같다.

퍼지 규칙은, ‘만약 ~라면, ~이다’와 같은 형태로 표현되는 것이다. 예를 들어, 퍼지 집합 \(A\)가 온도가 높다, \(B\)가 스위치를 낮게 내린다라면 ‘만약 온도가 높다면, 스위치를 낮게 내린다.’ 이는 퍼지 규칙이다.

퍼지 규칙은 퍼지 관계로 나타낼 수 있다. 예를 들어, 위 예제의 퍼지 규칙은 \(R:A \to B\)와 같은 퍼지 관계로 나타낼 수 있으며, 퍼지 논리식을 사용하면 다음과 같다.

\[\mu_{R}(x,y) = \min(1, 1 - \mu_{A}(x) + \mu_{B}(y))\]

주관적인 지식을 가지고 어떻게 추론하는가?

우리가 주관적인 지식을 갖고있을 때, 하게되는 통상적인 추론은 다음과 같다.

• 지금 많이 더운데, 에어컨 온도를 얼만큼 낮추는게 좋을까?
• 음식이 적당히 맛있었고, 서비스는 좋았는데 팁을 얼마나 주는게 좋을까?

가장 먼저 지식베이스를 구축해야 한다. 지식은 사실과 규칙과 같다. 그리고 사실은 퍼지 집합과 소속 함수와 같다.

퍼지 집합은 ‘덥다’, ‘세기가 강하다’와 같다. 파라미터는 온도를 넣어야 한다. 온도를 \(x\)라고 하고, 에어컨의 세기를 \(y\)라고 하자. 입력값이 x, 구하고 싶은 출력값을 y라고 생각하자.

\[\mu_{\text{덥다}}(x) = \dots\] \[\mu_{\text{강하다}}(y) = \dots\]

소속 함수를 정의한다.

이후 퍼지 규칙을 정의해야 한다. ‘만약 온도가 덥다면, 에어컨을 강하게 튼다.’ 이것이 퍼지 규칙과 같다. 즉, 덥다를 \(A\), 강하다를 \(B\)라고 하면 \(A\to B\) 퍼지 관계로 나타낼 수 있다.

\[u_{A\to B}(x,y) = \min(1, 1 - \mu_{A}(x) + \mu_{B}(y))\]

퍼지 관계의 소속 함수 또한 정의한다.

이제 \(x\)값을 통해 적절한 \(y\)값을 얻어내는 추론을 할 수 있게 되었다. 이를 퍼지 추론이라고 한다. 일반적인 추론법은 무게중심법(Centroid) 을 사용한다. 프로세스는 다음과 같다.

먼저 주어진 \(x=x_{0}\)값으로 소속도 값을 얻는다.

\[\alpha = \mu_{A}(x_{0})\]

이후 새로운 퍼지 집합 \(B'\)를 정의한다. (맘다니(Mamdani) 추론을 사용한다.)

\[\mu_{B'}(y) = \min(\alpha, \mu_{B}(y))\]

이는 기존의 \(\mu_{B} - y\) 그래프를 떠올려 봤을 때, \(\alpha\) 높이보다 윗 부분이 잘려나간 그래프와 같다. 이후 그 그래프의 기하학적 무게중심 위치의 \(y\)값을 결론으로 추론한다.

\[y_{\text{final}} = \frac{\int y \cdot \mu_{B'}(y) dy}{\int \mu_{B'}(y) dy}\]

이러한 퍼지 이론, 추론 기법은 가전제품, 제어 시스템에서 많이 활용한다