운영체제 19. 논리 주소와 물리 주소를 어떻게 연결할까

메모리 경영

논리 주소를 물리 주소와 언제 대응시킬까?

주소는 논리 주소와 물리 주소가 존재한다. 논리 주소는 한 프로그램에서만 사용하는 가상의 주소다. 물리 주소는 실제 램의 주소를 뜻한다. 논리 주소는 물리 주소와 대응되어야 한다. 언제 대응시켜야 할까?

프로그램은 컴파일되어 어셈블리어로 변환되고, 어셈블리어는 다시 컴파일되어 기계어로 변환된다. 기계어가 실행되면 링커가 프로그램을 메모리에 올려 프로세스가 된다. 프로세스는 CPU에 의해 실행된다.

컴파일 과정에서 미리 물리 주소로 변환하면 될까? 안된다. 다른 프로세스와 주소 충돌 가능성이 있다. 또, 물리 주소가 하나 변환되면 다시 컴파일해야 하는 불편이 있다.

그럼 컴파일은 논리 주소로 저장하고, 링킹 과정에서 물리 주소로 변환하면 될까? 안된다. 물리 주소가 바뀌면, 메모리 공간위에 있는 코드를 다시 덮어쓰기 해야한다. 유연함이 떨어진다.

따라서 논리 주소를 사용한 프로그램 코드를 메모리 위에 올린다. 이후 CPU가 명령어를 실행하는 순간에, 논리 주소를 물리 주소로 변환한다. 이 방법을 사용한다.

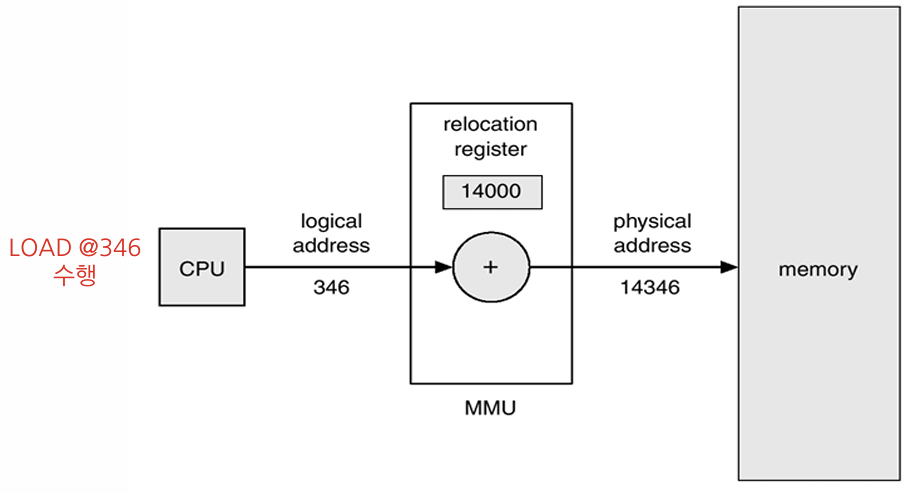
어떻게 실행시점에서 변환하는가? CPU가 논리 주소를 읽는다. 논리주소를 물리주소로 변환해주는 MMU (Memory Management Unit) 하드웨어에 논리 주소를 보낸다. 변환된 물리 주소를 통해 메모리 공간에 접근할 수 있다.

논리 주소와 물리 주소를 어떻게 대응하는가?

첫번째 아이디어는, 물리 메모리 공간을 고정된 크기로 분할하고, 그 공간에다 프로그램을 적재하는 것이다. Fixed Partition 방법이다. 이방법은 고정된 크기 이상의 프로그램은 적재할 수 없다. 또는 아주 작은 프로그램이면, 많은 메모리 공간 낭비가 생긴다. 따라서 쓰지 않는다.

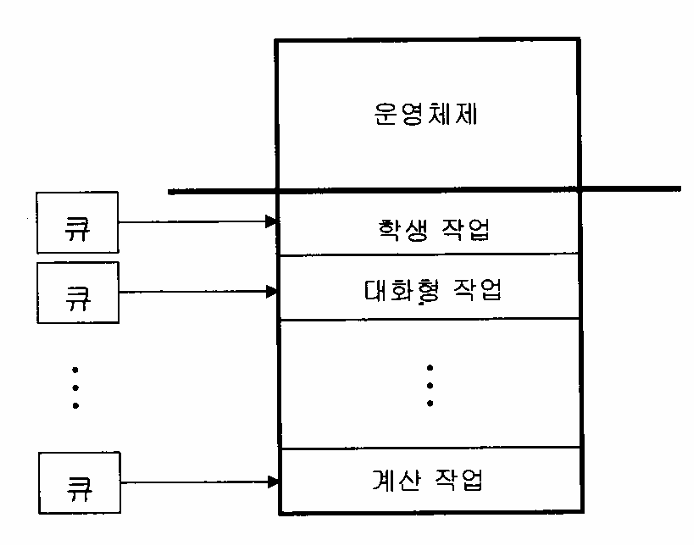
두번째 아이디어는, 프로그램 유형에 따라 그룹을 만들고, 그 그룹마다 분할하는 크기를 다르게 설정하는 것이다. Fixed Partition 방법의 확장그러나, 한 그룹에 몰릴 수 있는 문제가 있다. 그리고 특정 그룹에 속하는 프로세스의 크기가 정해진 그룹의 크기보다 작다는 보장이 없다. 따라서 쓰지 않는다.

세번째 아이디어는, 그냥 비어있는 적당한 곳에 넣는 방법이다. Variable Partition 방법이다. 적당한 곳이란 무엇인가? First fit, Best fit, Worst fit 세가지 선택지가 있다.

• First fit : 가장 첫번째 빈자리로 적재
• Best fit : 가장 딱 맞는 곳에 적재
• Worst fit : 가장 널널한 곳에 적재

시뮬레이션 결과 First fit, Best fit이 Worst fit보다 시간, 메모리 효율에서 더 좋다. First fit vs Best fit의 경우 메모리 효율은 비슷하지만 First fit가 속도가 더 빠르다.

가변 분할 방법은 단편화라는 큰 단점이 존재한다. 이론상 단편화때문의 용량의 1/3을 손해본다. 주기적으로 또는 메모리가 부족할 때마다 압축하면 되지 않을까? 압축하는 비용도 생각해야 한다. 압축 비용은 움직이는 총 프로그램의 크기와 같다. 따라서 압축 비용을 계산하는 알고리즘이 필요했던 시기도 있었다. 지금은 가변 분할 방법을 사용하지 않는다.

네번째 아이디어는, 페이징이다.

페이징이 무엇인가?

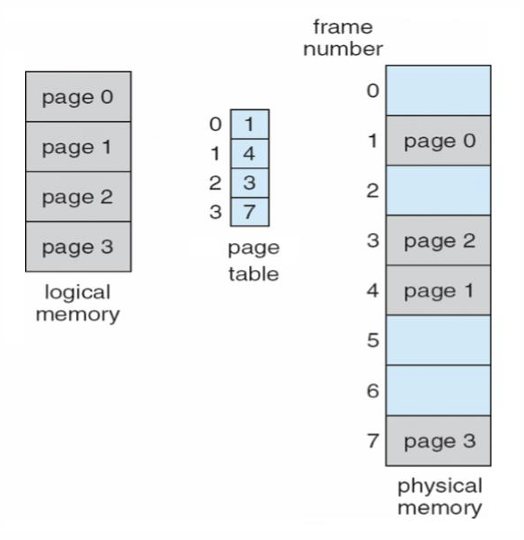
근본적인 원인은 프로그램을 연속적인 메모리로 올리면 단편화가 발생한다. 그렇다면, 프로그램을 분할하자. 분할한 프로그램의 단위를 Page라고 한다. 같은 크기로 물리적 메모리도 분할하자. 분할한 메모리 공간을 Frame라고 한다.

Frame에 Page를 적재한다. 적재 후 Page의 순서가 뒤죽박죽 섞이므로, 이를 관리하는 page table이 프로세스마다 필요하다. page table은 실제로 메인 메모리 공간 내에 저장되어 있지만, 접근하기 위해 table의 첫번째 메모리 주소가 필요하다. 이 메모리 주소는 page table base register가 가지고 있다. 프로세스의 PCB는 이 register 값을 알고 있다.

[!example] 16비트 주소 체계 시스템에서 p를 위해 4비트 d를 위해 12비트를 사용할 경우 이 시스템에는 몇 개의 페이지가 있고 각 페이지는 몇 바이트일까요?{title} \(p\)는 page number다. 따라서

\[2^4 = 16\]

page 개수는 16개다. 또, \(d\)는 offset이다. 따라서

\[2^{12} = 4096\]

페이지는 4096 바이트다.

주소 표현 약속

• 논리적 주소: \((p, d)\)
  • \(p\) : 페이지 번호
  • \(d\) : 페이지 내의 Offset
• 물리적 주소: \((f, d) = f \times S + d\)
  • \(f\): 프레임 번호
  • \(S\): 페이지 크기

[!question] 흠.. 근데 왜 논리 주소가 \((p, d)\) 인거지? {title} 0x0412041 이런식이 논리주소일거 아니야. 이걸 페이지 번호 p와 offset d로 바꾸는 과정이 있어야하는거 아니야?

“0x0412041 같은 논리 주소가 들어오면, 시스템은 이 주소를 비트 단위로 나누어 상위 비트는 페이지 번호 p로, 하위 비트는 오프셋 d로 변환하는 과정을 거칩니다.”

즉 0x0412041같은 표현이나 \((p, d)\)나 동일한 표현이다.

내부 단편화가 생기는건 어쩔 수 없나?

어쩔 수 없다. 평균적으로 각 프로세스에 대해 프레임 크기의 절반만큼 내부 단편화가 발생한다.

[!example] 페이지 크기가 512바이트인 시스템이라면 논리주소 중 몇 비트를 오프셋을 표현하는 비트로 사용하는가?{title}

\[2^9 = 512 \implies 9 \text{bit}\]

[!example] 이 때 만약 크기가 8,629바이트인 프로그램을 적재하려면 얼마의 내부 단편화가 일어나는가?{title}

\[512 - 8629 \% 512 = 75 \text{byte}\]

페이지의 크기는 얼만큼으로 설정하는가?

페이지 크기가 클수록 내부 단편화가 많이 발생한다. 그러나 페이지 테이블의 크기가 작아진다. 페이지 크기가 작을 수록 내부 단편화가 덜 일어난다. 그러나 페이지 테이블의 크기가 커진다.

현재는 4KB, 8KB를 주로 사용한다.

넣을 수 있는 프레임 위치는 어떻게 아는가?

비어있는 프레임 리스트를 커널에서 free-frame list로 관리한다.

논리 주소를 물리 주소로 어떻게 변환하는가?

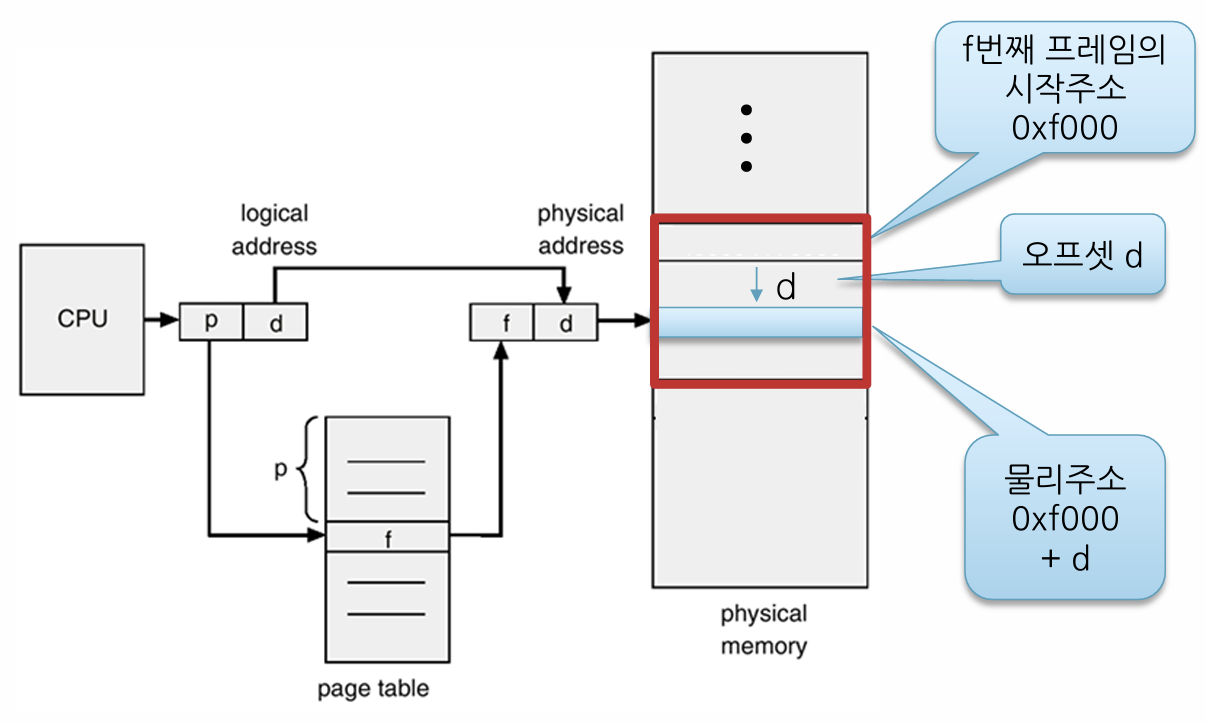
논리 주소는 \((p,d)\)와 같다. \(d\) 값은 그대로 넘긴다. \(p\) 값은 page table을 통해 frame number로 변환한다. \(f\)를 알면, \(f\)번째 프레임의 시작 주소를 알 수 있다. 그 시작 주소에 offset인 \(d\)를 더하면 물리 주소를 알 수 있다.

장단점이 무엇인가?

• 장점
  • 단편화 문제 해결 가능
  • 페이지 공유 가능
  • 메모리 보호 가능
• 단점
  • 페이지 테이블 사용의 속도 오버헤드
  • 페이지 테이블 용량 문제

페이지 공유가 무엇인가?

fork()하면 text 내용의 영역은 공유된다. 이 공유되는 영역은 하나의 페이지를 두 프로세스가 참조하는 식으로 구현할 수 있다. 이것이 페이지 공유다.

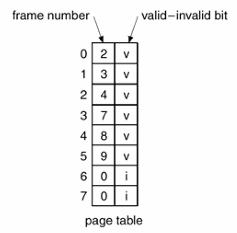
메모리 보호가 무엇인가?

페이지 테이블에 위와 같이 bit를 추가할 수 있다. valid-invalid bit 뿐만 아니라 read only bit, dirty bit (또는 modify bit)를 추가해서 메모리 보호가 가능하다. 예를들어 Context의 text 영역은 read only bit를 1로 설정하여 페이지를 보호한다.

해당 페이지가 메모리에 올라간 후 내용이 변경되었는지 나타내는 비트는 dirty bit다. 이는 나중에 가상 메모리에서 중요한 역할을 한다.

속도 오버헤드를 줄일 수 있는가?

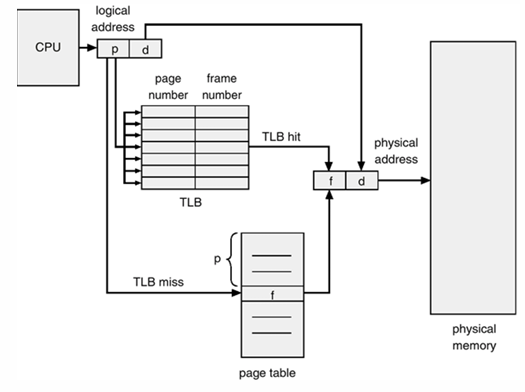
왜 페이지 테이블을 사용하면 느린가? 페이지 테이블은 보통 메인 메모리에 저장된다. 즉 메인 메모리에 있는 페이지 테이블에 먼저 접근해서 프레임 번호를 얻어내고, 그 이후에 프레임 번호를 물리 주소로 변환해서 메인 메모리에 다시 접근한다. 결과적으로 메인 메모리에 두번 접근한다. 한번 접근하는 것보다 두배 더 느리다.

이를 해결하기 위해 TLB를 사용한다. TLB는 마치 캐시와 같다. 페이지 테이블에 접근시 관련 내용을 TLB에 저장해둔다. 이후 다시 페이지 테이블에 접근하기 전에 먼저 TLB에 접근한다. TLB는 고속 레지스터다. 접근하는데 부담이 없다. 만약 TLB hit가 발생하면 메인 메모리에 한번만 접근해도 된다. 속도가 개선된다.

페이지 테이블 용량 문제를 해결할 수 있는가?

32비트 체계의 논리 주소 공간의 크기는 \(2^{32}\)다. 한 페이지 사이즈를 \(4\text{KB}\)라고 하자. 이는 \(2^{12}\) 비트와 같다. 따라서 페이지 테이블은 \(2^{32} / 2^{12} = 2^{20} = 4 \text{MB}\) 만큼의 용량이 필요하다. 프로세스 100개 켜두면 페이지 테이블만 400MB다. 64비트 체계는 적재가 불가능하다. 따라서 페이지 테이블도 연속적으로 적재하는 것이 아니라, 분할해서 적재하는 전략이 필요하다. 어떻게 가능할까?

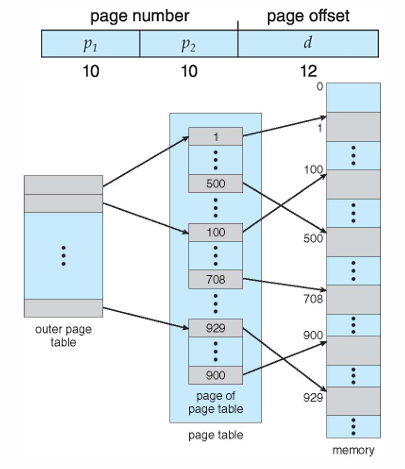
(1) 계층적 페이징 접근법 (Hierarchical paging)

논리 주소를 \((p_{1}, p_{2}, d)\)로 만든다. 즉 \(p_{1}\)으로 outer page table에 접근해서 하위 테이블의 주소를 얻는다. 그 주소로 접근했을때 있는 inner page table에 \(p_{2}\)를 통해 frame number를 얻는다.

64비트를 사용하면 이 계층을 4개 이상까지 늘려야 한다. 즉, 메모리를 5번 접근해야 하는 단점이 있다.

(2) 해쉬 페이지 테이블(Hashed Page Tables) 논리 주소 \((p, d)\)를 hash function에 넣는다. hash table에 접근한다. hash table의 value는 연결리스트다. 연결리스트는 페이지 번호, 프레임 번호, next 포인터 세가지 필드값을 가진다. 즉 연결리스트에서 \(p\)와 매치되는 노드를 찾고, 그 노드의 프레임 번호를 꺼낸다.

운영체제가 새로운 페이지를 물리 메모리에 할당할 때, 매핑 정보를 해시 테이블에 추가한다. 장점은 큰 공간을 Hash를 적용하면 작은 공간으로 Mapping할 수 있다는 것이다. 단점은 캐시 지역성이 부족하여 TLB 미스가 많이 뜬다. 그리고 해시 함수에 크게 의존한다.

(3) 클러스터 페이지 테이블(Clustered Page Tables) 64비트의 \(2^{44}\)라는 공간은 너무 크기 때문에 클러스터 페이지 테이블을 사용한다. 논리 주소를 \((\text{virtual block number}, \text{block offset}, d)\)로 쪼갠다. virtual block이란, page block이다. page block이란, 연속된 여러 페이지의 집합(16) page block은 frame number를 가지고 있다. block offset이란, page block 내에서의 페이지 번호다. 0-15

virtual block number를 hash function에 넣는다. 얻은 hash 값으로 hash table에 접근한다. hash table에는 연결리스트가 들어있다. 연결리스트가 갖는 필드는 virtual block number, page block, next pointer 세가지 정보를 가진다. 즉 virtual block number를 가지고 연결리스트와 비교해가며 page block를 얻는다. 이후 알고있는 block offset으로 page block 내에서 frame number를 얻는다.

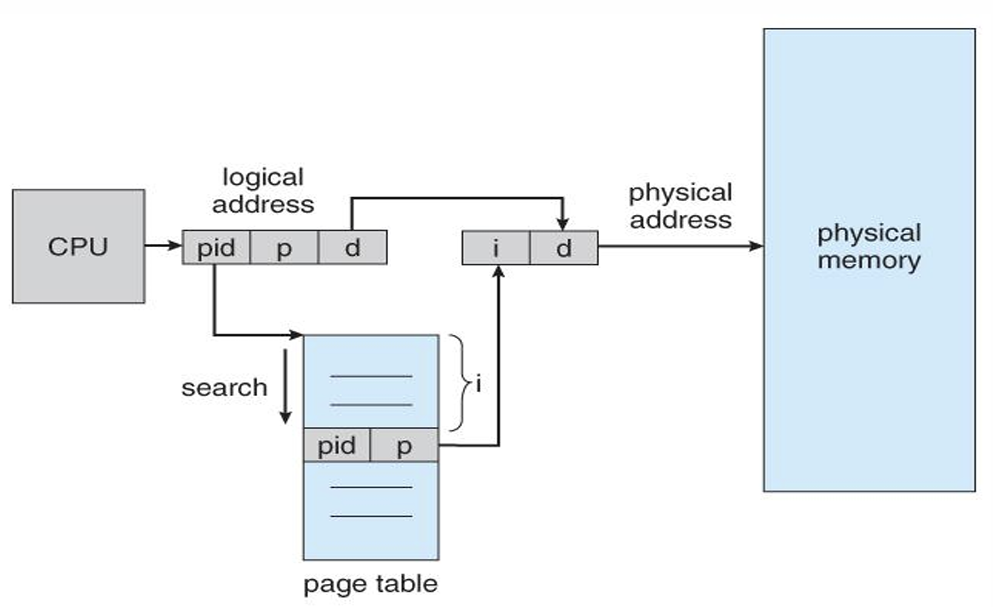
(4) 역 페이지 테이블(Inverted Page Table)

각각의 프로세스마다 페이지 테이블을 만들지 말자. 대신 시스템 내의 하나의 프레임 테이블을 만들고, 어떤 프로세스의 어떤 페이지와 연결되었는지를 저장하자. 즉 프레임 테이블의 value는 \((\text{pid}, p)\) 값을 저장한다.

논리 주소는 \((\text{pid}, p, d)\)를 사용한다. 원본 논리 주소 0x49128421를 \(p\)와 \(d\)로 쪼개고, 앞에 pid를 붙이면 논리주소 완성이다.

이후 \((\text{pid}, p)\) 쌍을 갖는 프레임 테이블의 index를 찾기 위해 프레임 테이블을 Search한다. 찾으면 Index를 얻을 수 있다. 즉 Frame number를 얻는다.

단점은 Search를 추가했기 때문에 속도가 느려진다. 평균 서치 시간은 \(2^{20} / 2\)다. 이를 해결하는 아이디어는 Search를 \(O(1)\)에 하는 방법을 적용하는 것이다. 즉, Hash를 도입한다. 단, 해쉬 테이블 접근으로 인해 메모리 접근 횟수가 한번 증가한다.

세그먼테이션

다섯번째 아이디어는, 세그먼테이션 방법이다.

단순히 프로세스를 같은 크기로 자르면, 한 프레임의 절반은 text 영역이고 절반은 데이터 영역이 될 수 있는데 그러면 read only bit를 1로 할지 0으로 할지 애매하지 않은가?

따라서 페이지를 다 똑같이 페이지로 보지 말고, 유형별로 구분하자. 그것이 세그먼트다.

• 코드 세그먼트
• 데이터 세그먼트
• 스택 세그먼트
• 힙 세그먼트

한 프로세스는 여러개의 세그먼트를 갖는다. 프로세스마다 세그먼트 테이블을 단 하나 갖는다. 어떤 프로세스는 코드 세그먼트가 100개 나올수도 있지만, 어떤 프로세스는 코드 세그먼트가 20개 나올 수 있다. 아니 세그먼트마다 크기가 다 다른데, 그 세그먼트들을 하나의 세그먼트 테이블에 집어넣으면 그 세그먼트를 어떻게 구분짓는가?

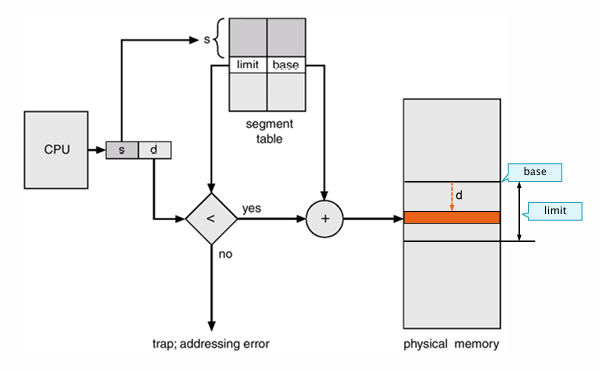
먼저 논리 주소는 \((s, d)\)로 구성된다. \(s\)는 세그먼트 번호다. 세그먼트 번호는 로더가 세그먼트마다 번호를 매긴다.

\(s\)를 가지고 세그먼트 테이블에 접근한다. 세그먼트 테이블에는 limit 값과 base 값이 들어있다. 즉, \(s\)를 알면 limit와 base를 알 수 있다. base는 해당 세그먼트가 물리 메모리에서 시작하는 주소와 같고, limit는 해당 세그먼트의 크기다.

만약 offset이 limit보다 크다면, 해당 세그먼트 밖 범위에 메모리에 접근하게 된다. 따라서 offset과 limit을 비교해서 offset이 더 크다면, 메모리 보호 관점으로 error 처리를 해준다. 아니라면 base값과 d 값을 더하여 물리 메모리 주소를 얻는다.

세그먼테이션 방법이 왜 다시 단편화가 발생하는가?

세그먼트의 크기는 제각각 다르고, 세그먼트는 연속된 메모리 공간에 할당되어야 한다. 따라서 이 세그먼트를 메모리 공간 위로 적재하는 과정에서 단편화가 발생한다. 이것이 외부 단편화다.

단편화 문제를 어떻게 해결하는가?

페이징과 세그먼테이션을 같이 사용하는 Paged Segmentation 방법을 사용한다. 프로세스를 세그먼트로 나누고, 세그먼트를 고정된 크기의 페이지로 나눈다. 즉 세그먼트 테이블은 페이지 테이블의 시작 주소를 알려준다. 논리 주소를 \((s, p, o)\)로 나눈다.

Paged Segmentation 방법은 MULTICS, Intel, ARM 계열마다 구현 법이 다르다.