영상처리 2. Point Processing이 무엇인가

Point Processing

해당 픽셀의 값만 사용해 새로운 값을 계산하는 변환이다. 변환 후 픽셀값을 \(G(x,y)\)라고 하면, 변환 함수 \(T\)를 적용하여 계산한다.

\[G(x,y) = T(f(x,y))\]

어떤 변환 함수들이 존재할까?

(1) 산술 연산 각 픽셀에 단순히 임의의 상수 \(c\)를 더하거나, 빼거나, 곱하거나, 나누는 연산을 적용할 수 있다.

흑백 영상에 상수를 더하면 전체적으로 밝기가 늘어나고, 상수를 뺴면 전체적으로 밝기가 줄어든다. 상수를 곱하면 대비가 커진다. 따라서 밝은 부분은 더 밝게 보이고, 어두운 부분은 더 어둡게 보인다. 상수를 나누면 대비가 줄어든다.

[!question] 만약 음수 값이나, 255보다 큰 값이 만들어지면 어떻게 하나?{title} Clamping한다. 음수는 0, 큰 값은 255로 설정한다.

(2) 논리 연산 두 영상이 있을 때, 각 픽셀의 값을 2진수로 변환하여 AND, OR, NOT, XOR 논리연산을 적용할 수 있다.

• AND: 특징을 추출하거나, 마스킹에 사용한다. 마스크할 부분의 픽셀 값을 \(11111111\)로 설정하고 AND 연산을 한다.
• OR: 여러 특징을 합치거나, 특정 영역을 강조할 때 사용한다.
• XOR: 두 영상의 같은 위치 픽셀 값이 다르면 1, 같으면 0. 변화를 감지하거나 차이점 강조할 때 사용한다.
• NOT: 흑백이 반전된 이미지를 얻는다.

[!example]- example{title}

(3) Gray-level Transform 입력 픽셀값을 \(r\), 출력 픽셀값을 \(s\)라 할 때 흑백 영상에 적용될 수 있는 변환들은 다음과 같다. 이때 \(r\)은 0~1 사이로 정규화된다.

(3-1) Negative

\[s = L - 1 - r\]

\(L\) : 픽셀 값이 가질 수 있는 Range, 256. 따라서 \(L-1\)을 사용함. 흑백이 반전된 이미지를 얻는다.

(3-2) Log Transformation

\[s = c \cdot \log(1+r)\]

\(c\) : 스케일 상수 (보통 1) 어두운 부분이 밝아지고, 밝은 부분은 압축되어 전체적으로 어두운 영역의 디테일이 강조된다.

[!example]- example{title}

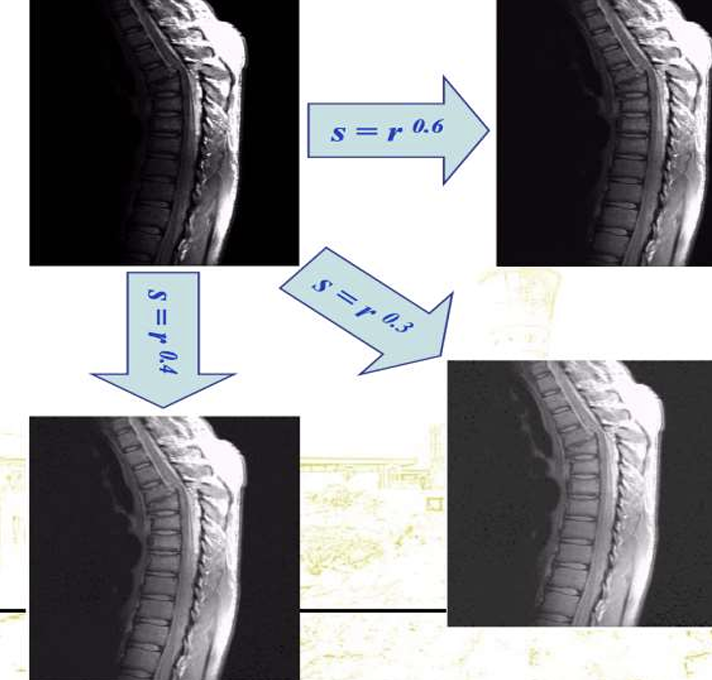
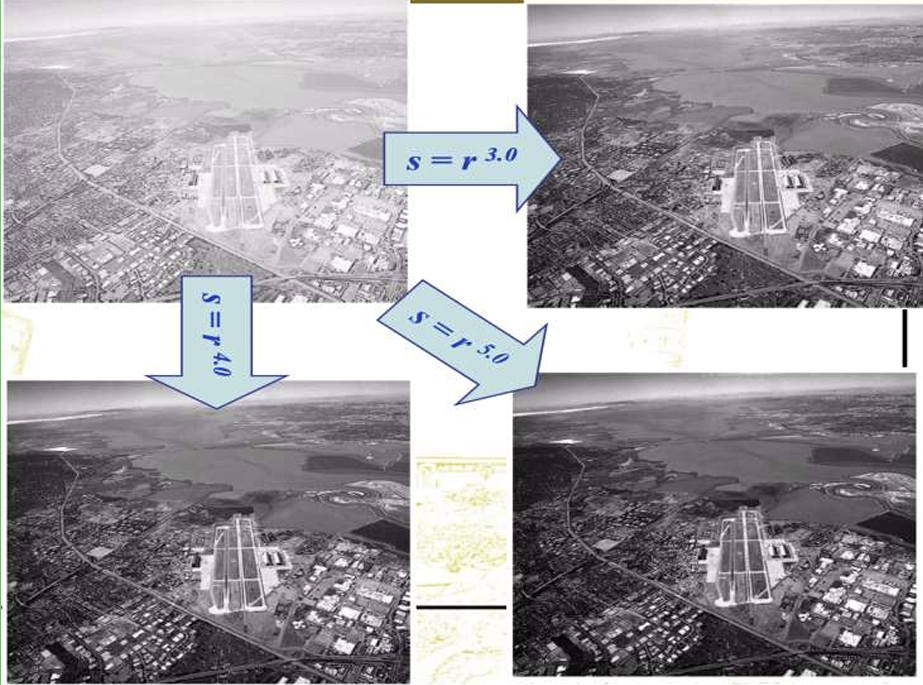
(3-3) Power-law, Gamma Transformation

\[s = c \cdot r^\gamma\]

\(c\) : 스케일 상수 (보통 1) \(\gamma\) : 감마 값 감마 값에 따라 효과가 다르다. \(\gamma < 1\)이면, 전체적으로 영상이 밝아진다. \(\gamma > 1\)이면, 전체적으로 영상이 어두워지며, 명암 대비가 강조된다. 감마가 1이면 스케일 상수에 따라 스케일링 될 뿐이다.

감마를 통해 영상의 밝기를 조절하는 것을 감마 보정(gamma correction)이라 한다.

[!example]- example{title}

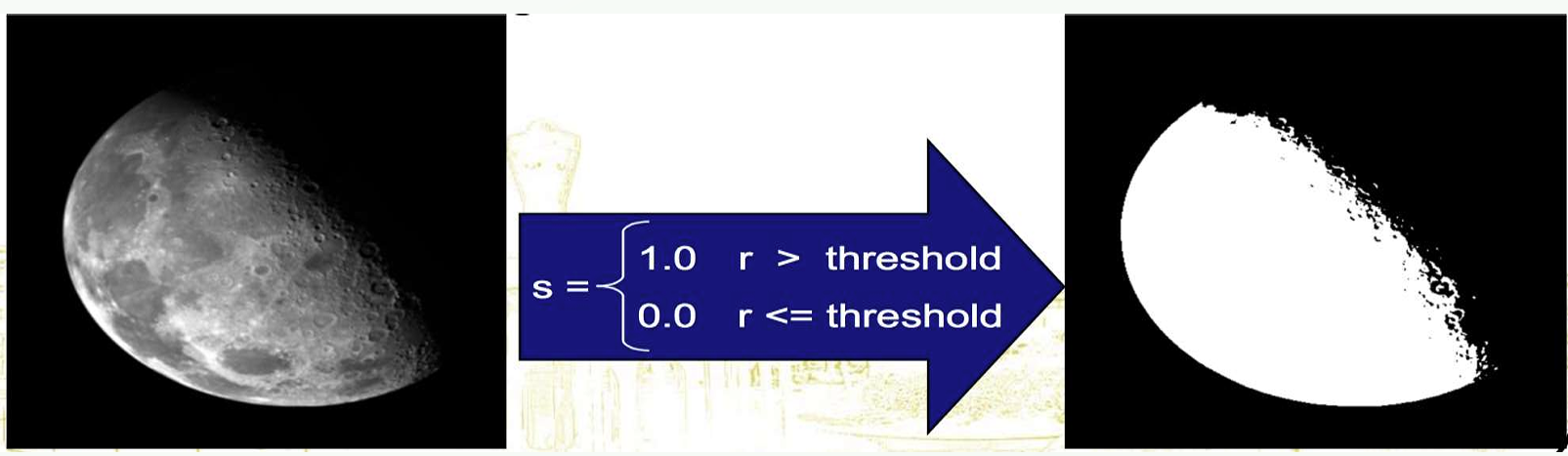
(3-4) Thresholding

\[s = \begin{cases} 1 & \text{if } r > T \\ 0 & \text{if } r \leq T \end{cases}\]

\(T\) : 임계값 임계값을 기준으로 큰 값을 1, 작은값을 0으로 만들어 영상을 구분한다.

[!example]- example{title}

(3-5) Gray-level Slicing

\[S = \begin{cases} L - 1 & \text{if } A \leq r \leq B\\ 0 & \text{otherwise} \end{cases}\]

\([A,B]\) 영역의 픽셀들만 뚜렷하게 보이게 한다. 또는 나머지 픽셀을 0이 아니라 \(r\)로 유지하면, 배경을 유지하면서 특정 특징만 밝게 강조한다.

(3-6) Bit-plane Slicing 픽셀의 특정 비트만 추출한다. 예를들어, 8비트 픽셀에서 4번째 비트만 추출한다. 무슨 효과를 얻는가?

주로 상위 비트에 영상의 주요 특징이 모두 몰려있다. 그리고 하위비트는 디테일, 노이즈, 워터마크같이 숨겨진 정보 등이 담겨있다.

하위 비트에 워터마크를 넣거나 찾아내거나, 노이즈를 분석할 때 사용 가능하다. 그리고 어떤 비트가 영상 품질에 가장 큰 역할을 주는지 분석하여, 필요 없는 비트는 날려 영상 압축에 사용될 수 있다.

[!example]- example{title}

[!NOTE] 기타 변환{title}

• 포스터라이징(Posterizing)
  • 영상에서 화소가 가질수 있는 명암값의 범위를 축소
• 비트클리핑(Bit-clipping)
  • 화소의 최상위 비트중 일정부분을 0으로 설정
• 등명암윤곽화(iso-intensity contouring)
  • 특정한 입력 명암값을 흰색 또는 검정색으로 지정
  • 특정구간에 존재하는 영상의 윤곽선을 찾기위해 사용
• 솔라라이징(solarizing)
• 파라볼라(parabola)

(4) Contrast Transformation 대비를 변환한다. 대비는 다음과 같다.

\[C = \frac{I_{max} - I_{min}}{I_{max} + I_{min}}\]

(4-1) Contrast Stretching

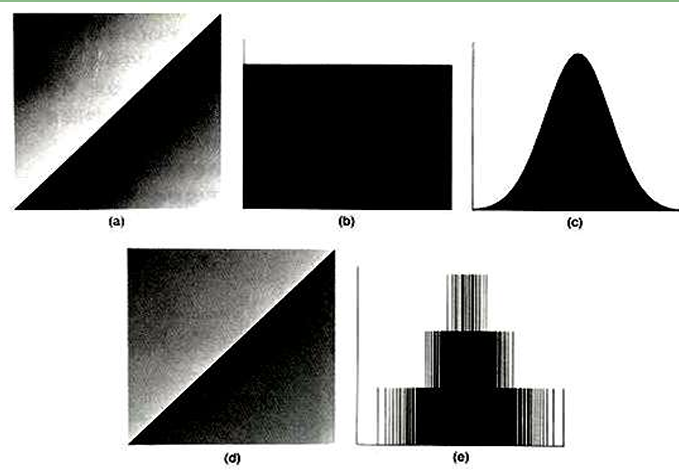
\[s = \frac{(r - \text{low}) \cdot (L - 1)}{\text{high} - \text{low}}\]

\(\text{high}\) : Stretching할 구간의 상한 값 \(\text{low}\) : Stratching할 구간의 하한 값 하한값과 상한값이 0~255 값으로 스트레칭된다.

위와 같이 낮은 명암 대비와, 가우시안 분포를 가질 수록 잘 적용된다.

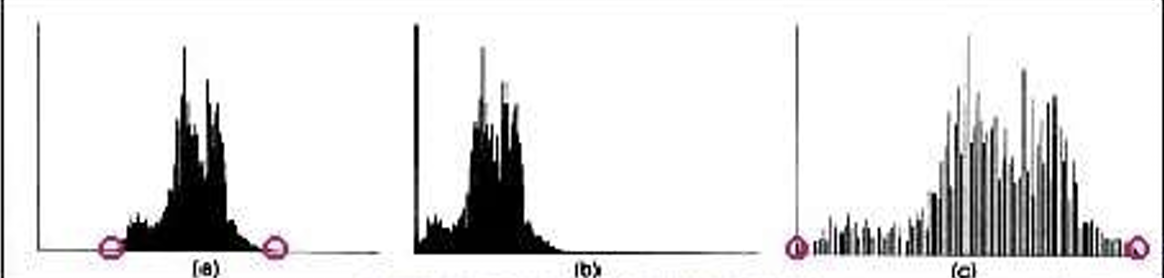
(4-2) Ends-in Search high, low 값을 픽셀 범위의 최대 최소값을 지정하는게 아니라, 임의의 임계값을 설정한다.

\[s = \left\{ \begin{array}{cl} 0 & \text{if } r \leq \text{low} \\[1.2ex] \displaystyle\frac{(r - \text{low}) \cdot (L - 1)}{\text{high} - \text{low}} & \text{if } \text{low} < r \leq \text{high} \\[1.2ex] 255 & \text{if } r > \text{high} \end{array} \right.\]

이를 통해 극단적으로 밝거나 작은 노이즈를 걸러낼 수 있다. 모든 범위의 명암값을 갖지만, 히스토그램이 특정 범위에 몰려있는 영상에 적용하면 좋다.

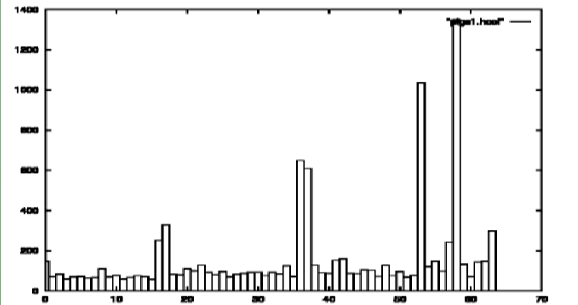
(5) Histogram Transformation Histogram이 무엇인가? 밝기가 0인 픽셀이 몇개고, 1인 픽셀이 몇개고, …, 255인 픽셀이 몇개인지 나타낸 막대 그래프가 히스토그램이다.

만약 특정 값이 높다면, 그 범위의 밝기가 유독 많다는 뜻이 된다.

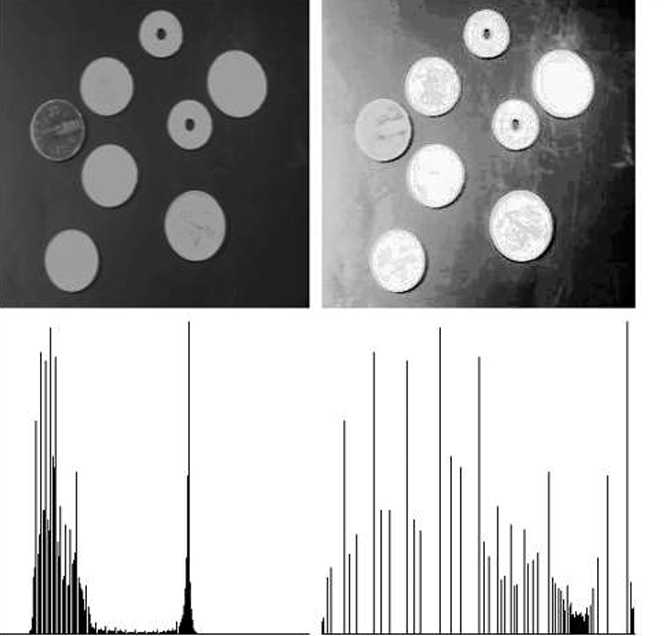
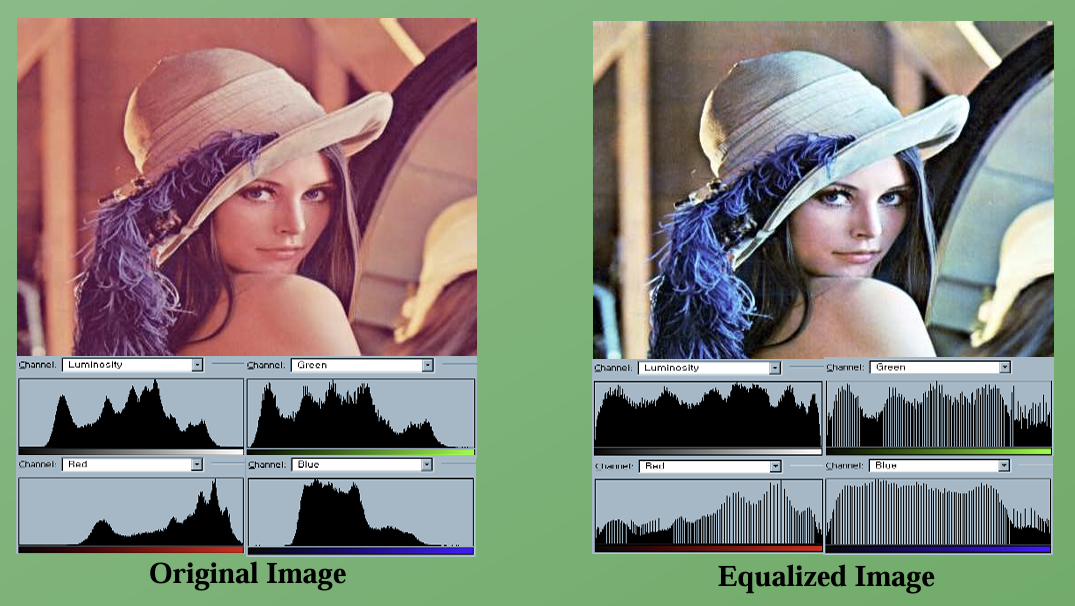
(5-1) Histogram Equalization

\[T(r) = \frac{\text{Sum}(r) - \text{Sum}_{\text{min}}}{N - \text{Sum}_{\text{Sum}}}\] \[s = \text{round} \left( T(r) \cdot (L-1)\right)\]

\(\text{Sum}(r)\) : 0 ~ r까지의 누적 히스토그램 값 \(T(r)\) : 변환 함수. 0~1까지의 값으로 정규화된 값을 출력함. \(N\) : 전체 픽셀 수 \(\text{round}(x)\) : 반올림 함수

확률 분포 함수를 사용하여 히스토그램을 골고루 배치한다. 이를 적용하면 영상의 히스토그램이 가능한 평평하게 분포되도록 한다. 특정 구간에 몰려있던 픽셀 값이 전체 범위로 넓게 퍼진다.

[!NOTE]- \(\text{Sum}_{\text{min}} = 0\)으로 가정할 때 Pseduo 코드는 다음과 같다.{title}

for (i = 0; i < N; i++)
{
    histogram[buffer[i]]++;
}

scale_factor = 255.0 / N;
for (sum = 0, i = 0; i < 256; i++)
{
    sum += histogram[i];
    // 0.5를 더하고 정수형 변환하면 반올림 효과가 있다.
    T[i] = (int) (sum * scale_factor) + 0.5;
}

for (i = 0; i < N; i++)
{
    buffer[i] = T[buffer[i]];
}

[!example]- example{title}

(5-2) Histogram Specification 어떤 영상의 히스토그램 분포를 특정 영상의 히스토그램 분포처럼 매핑하고 싶다. 이는 특정 영상의 전체적인 톤, 분위기, 질감을 맞추는데 유용하다.

그게 어떻게 가능할까? 우선 두 영상을 평활하여 누적 분포 함수를 구한다. (CDF) 그리고 원본 영상의 각 픽셀마다 그 픽셀의 값 중 비교할 영상의 히스토그램 값과 가장 비슷한 누적 분포 함수의 값을 찾는다. 그리고 그 두 값을 Mapping하는 Table을 만든다. 이를 LUT라고 한다. 이후 원본 영상의 모든 픽셀에 대해 LUT를 적용하면 새로운 밝기값으로 변환된다.

[!NOTE]- pseduo code{title}

CDF_source[], CDF_target[]; // source 영상과 target 영상을 히스토그램 평활화한 결과다.
int i, j;

for (i = 0; i < 256; i++)
{
    int min_diff = 1000000;
    int best_j = 0;
    for (j = 0; j < 256; j++)
    {
        int diff = abs(CDF_source[i] - CDF_target[j]);
        if (Cdiff < min_diff)
        {
            min_diff = diff;
            best_j = j;
        }
    }
    LUT[i] = best_j;
}

for (i = 0; i < N; i++)
{
    buffer[i] = LUT[buffer[i]];
}