양자역학 8. 슈뢰딩거 방정식을 어떻게 푸는가
슈뢰딩거 방정식을 어떻게 푸는가?
슈뢰딩거 방정식은 \(V\)에 따라 비교적 간단하게 풀 수도, 아주 어려울 수도 있다. \(V\)는 보통 \(\frac{1}{r^n}\)에 비례하는데, n이 작을수록 short range, 클 수록 long range라고 표현한다. long range일 수록 풀기 어려워진다. 그 이유는, 포텐셜 범위가 넓어지므로 그만큼 상호작용하는 전자 수가 많아지기 떄문이다. 간단하게 포텐셜이 시간에 무관한 함수로 주어지는 경우를 먼저 알아보자.
포텐셜 에너지가 시간에 무관한 함수로 주어질 때
이 경우, 파동함수를 분리 가능한 해로 가정해도 무방하다.
\[\Psi(x,t)=\Psi(x)\Psi(t)\] \[\psi = \Psi(x), ~ \varphi = \Psi(t)\]결론적으로, (1) 포텐셜 에너지가 시간에 무관한 함수로 주어진다면 Time-indenpendent Schrodinger Equation를 풀어 \(\psi_{n}(x)\)를 찾는다. 이후 경계조건과 정규화를 사용하여 계수를 구한다. 이때 \(\psi\) 또는 \(\frac{d\psi}{dx}\)가 연속임을 이용한다. 이후 에너지 \(E_{n}\)을 구한다. 일반해에 \(t=0\)일 때 푸리에 방법을 사용하여 \(c_{n}\)을 찾는다. (\(c_{n}\)은 시간에 대해 무관하다.) 그러면 최종적인 최종적인 일반해 \(\Phi(x,t)\)를 구할 수 있다.
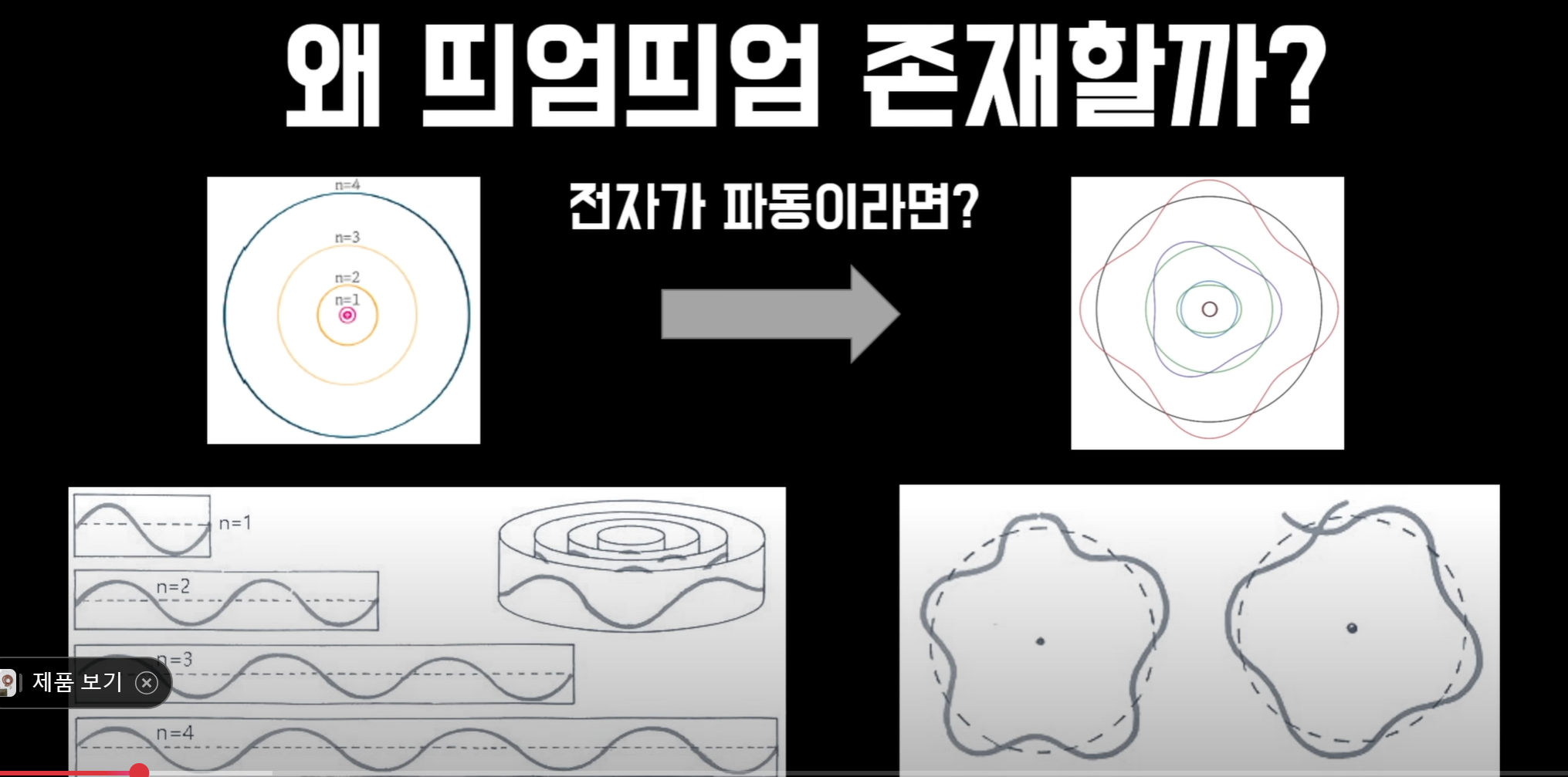
[!tip] 포텐셜이 제한 또는 구속되면 파동함수는 양자화된다. \(\Psi_{n}\){title} 왜? 모든 물질은 파동함수로 기술되고, 파동 함수는 정확히 파장과 맞아 떨어지는 파장들만 허용한다. 그렇지 않은 파장은 구속되었기 때문에 다시 반사되고
(돌아오고), 파장이 다르기 때문에 상쇄되어 없어진다. 그 과정 중에 파장이 딱 맞아떨어져서 상쇄되지 않는 파장만 남기 떄문이다.이는 전자가 왜 특정 궤도 위에서만 존재할 수 있는지를 설명한다. 전자 또한 파동이기 때문이다. 끝이 맞지 않으면 계속 돌다가 상쇄되버리고 상쇄되지 않는 것만 남는다.
[!NOTE]- 증명{title} 아래는 슈뢰딩거 방정식이다.
\[i\hbar \frac{\partial \Psi(x,t)}{\partial t}=- \frac{\hbar^2}{2m} \frac{{d^2 \Psi(x,t)}}{dx^2} + V \Psi(x,t)\]변수분리한 해를 대입한다.
\[i\hbar \psi\frac{\partial \varphi}{\partial t}=- \frac{\hbar^2}{2m}\varphi \frac{{d^2 \psi}}{dx^2} + V(x) \psi \varphi\]양 변을 \(\psi \varphi\)로 나누면 좌변은 시간에 대해서만, 우변은 위치에 대해서만 의존하는 식으로 분리된다.
\[i\hbar \frac{1}{\varphi} \frac{\partial \varphi}{\partial t} = - \frac{\hbar^2}{2m} \frac{1}{\psi} \frac{d^2\psi}{dx^2} +V(x)\]x, t는 독립이므로 등식이 만족하기 위해선 둘다 상수어야 한다. 분리상수 \(E\)를 도입하자.
\[i\hbar \frac{1}{\varphi} \frac{\partial \varphi}{\partial t} \equiv E\]따라서 다음과 같다.
\[E \psi = -\frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} + V(x)\psi\]
\(\hat{p}^2 = -\frac{\hbar^2}{2m} \frac{d^2}{dx^2}\)이므로, 다음과 같이 정리할 수 있다.
\[E\psi = \left( \frac{\hat{p}^2}{2m} + V(x) \right)\psi\] \[E\psi = \hat{H} \psi\]\(\hat{H}\)는 해밀토니안 연산자이며, 고전 역학에서 전체 에너지(운동 + 퍼텐셜 에너지)를 뜻하는 물리량이다. \(E\)는 해밀토니안 연산자 \(\hat{H}\)과 같으므로, 분리상수 \(E\)는 양자계의 전체 에너지다!
\[E = \hat{H} = \frac{\hat{p}^2}{2m} + V(x)\]포텐셜 에너지가 시간에 무관한 상태는 물리적으로 무슨 의미를 갖는가?
정상상태와 같다. 정상 상태란, 변수가 시간에 대해 변하지 않는 경우이다.
\[\frac{\partial p}{\partial t}=0\]예를들어, 전자기학에서 전류의 정상상태란 전류가 시간에 대해 변하지 않는 steady current \(\frac{\partial \vec{J}}{\partial t}=0\)인 경우라고 배웠다.
그것이 멈춰있는 것은 아니다. 멈춰있다는 것은 속도가 0이라는 뜻이다. 상태가 시간에 따라 변하지 않는 것이 정상 상태라고 볼 수 있다. 속도를 예로, 속도가 0은 아니지만, 상수값인 경우 정상상태
\(\Psi(x,t)\)의 일반해는 무엇인가?
슈뢰딩거 방정식을 만족하는 파동 함수는 \(\Psi_{1}, \Psi_{2}, \dots, \Psi_{n}\) 여러개 존재한다. 따라서 일반적인 General solution은 \(\Psi(x) = c_{1}\Psi_{1} + c_{2}\Psi_{2} + \dots + c_{n}\Psi_{n}\) 선형 결합하여 표현한다.
\[\Psi(x,t) = \sum_{n=1}^{\infty}c_{n}\psi_{n} e^{-i E_{n} t/\hbar}\]\(c_{n}\)이 무엇인가?
\(c_{n}\)의 절댓값의 제곱은, 에너지를 측정했을 때 \(E_{n}\)이 나올 확률이다. 각 양자 상태는 하나의 \(E_{n}\) 에너지 상태에 대응된다. 따라서, \(c_{n}\)은 측정했을 때 \(\Psi_{n}\) State가 나올 확률이다. 증명은 추후 서술한다.
\[\sum_{n=1}^{\infty} \lvert c_{n} \rvert^2 = 1\]만약 \(c_{n} = 0\)이면 에너지가 존재하지 않는다. 따라서 측정 대상이 無다.
정상 상태에서 \(\Psi_{0}\)이 관측돨 확률이 0.6이고, \(\Psi_{1}\)이 관측될 확률이 0.4면 일반해 \(\Psi\)는 다음과 같다.
\[\Psi = \sqrt{ 0.6 } \Psi_{0} e^{-i E_{0} t / \hbar} + \sqrt{ 0.4 } \Psi_{1} e^{-i E_{0} t / \hbar}\]위 표현식이 마치 벡터와 같지 않는가?
\[\vec{A} = c_{x} \hat{x} + c_{2} \hat{y}\]\(\Psi_{1}, \dots\)는 기저 벡터 \(\hat{e}_{1}, \dots\)와 같은 역할을 할 수 있다. \(\Psi\)는 힐베르트 공간 위의 한 벡터이기 때문이다. 벡터는 기저가 바뀜에 따라 표현이 바뀔 수 있다. 따라서 슈뢰딩거 방정식의 해도 Unique하지 않다.
\[\vec{A} = e_{1} \hat{x} + e_{2} \hat{y} = c_{x}' \hat{x}' + c_{2} \hat{y}'\]하지만 combine된 해만 같으면 된다.
\(c_n\)을 어떻게 구하는가?
\(\psi(x)\)는 Complete하다. 즉, 정규화되고 직교하는 함수들이다. 따라서
\[\int_{-\infty}^{\infty} \psi_{n}^* \psi_{m} dx = \delta_{nm}\]을 만족하고, 이를 통해 일반해 공식에서 t=0일 때 푸리에 방법을 사용하여 \(c_{n}\)을 구할 수 있다.
[!example] Example{title}
\[\int \psi_{m}^* \Phi(x,0) dx = \int \sum c_{n} \psi_{n} \psi_{m}^*dx\] \[= \sum c_{n} \int \psi_{n} \psi_{m}^* dx\] \[= \sum_{n=1}^{\infty} c_{n} \delta_{nm}= c_{m}\] \[\therefore ~~ c_{n} = \int \psi_{n}^* \Phi(x,t) dx\]