양자역학 18. 디렉 퍼텐셜 내의 입자는 어떻게 거동할까

V가 디렉 델타함수면 어떻게 될까?

\[\delta(x) = \begin{cases} 0 & x \neq 0\\ \infty & x=0 \end{cases}\] \[\int_{-\infty}^{\infty} \delta(x) dx = 1\]

디렉 델타 함수는 위 성질을 가진다. 다음 퍼텐셜을 생각해보자.

\[V(x) = - \alpha \delta(x)\]

\(\alpha\)는 임의의 상수이다.

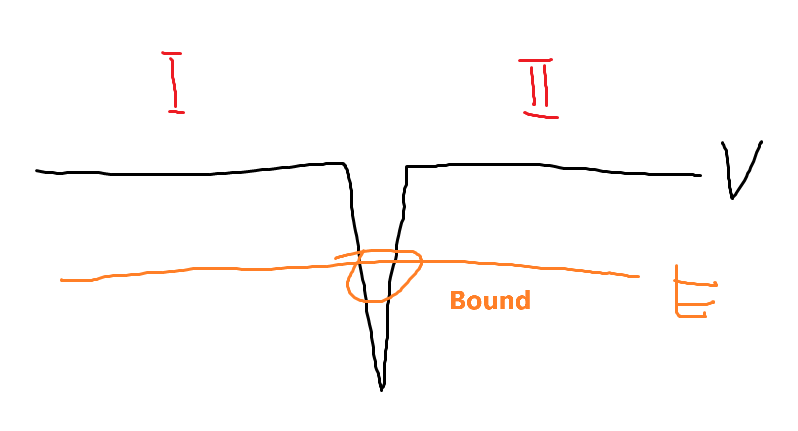
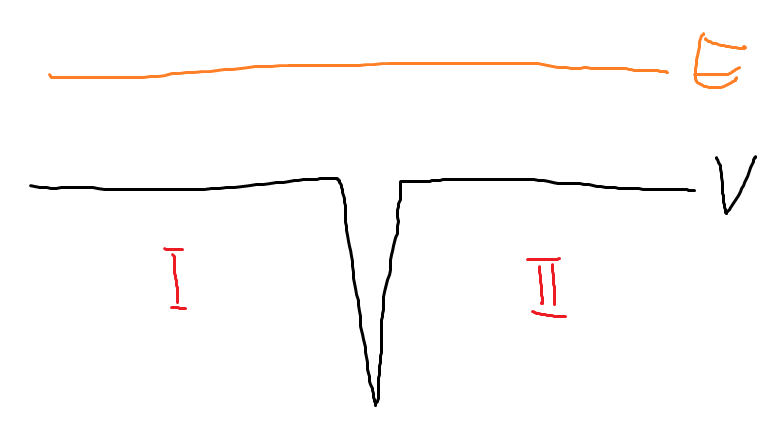
구역 1과, 구역 2에선 \(V=0\)이다. \(x=0\)일 땐 퍼텐셜이 \(\infty\)이다. 또한, 외부에서 에너지 \(E\)를 가지고 들어오는 상황을 생각하자. 따라서 \(E>0\) 또는 \(E<0\)일 수 있다. 이를 고려하여, Time-independent Schrodinger Equation을 풀어야 한다.

\[- \frac{\hbar^2}{2m} \frac{d^2}{dx^2} \psi + V(x)\psi = E \psi\]

그 전에, 미분방정식을 풀려면 Boundry Condition을 알아야 한다. \(\psi\)에 대한 두가지 Boundry Condition을 사용할 수 있다.

\[\psi \text{는 항상 연속이다.}\] \[\frac{d\psi}{dx}\text{는 퍼텐셜이 무한대인 점을 제외한 곳에서 연속이다.}\]

구역 1과 구역 2의 \(\psi\)를 각각 \(\psi_{1}\), \(\psi_{2}\)라고 하면 다음이 성립해야 한다.

\[\psi_{1}(0) = \psi_{2}(0)\]

두번째 바운더리 컨디션을 사용하기 위해, 슈뢰딩거 방정식을 사용하자.

\[- \frac{\hbar^2}{2m} \frac{d^2}{dx^2} \psi - \alpha \delta(x)\psi = E \psi\] \[\implies - \frac{\hbar^2}{2m} \int_{-\epsilon}^{\epsilon} \frac{d^2}{dx^2} \psi dx - \alpha \int_{-\epsilon}^{\epsilon} \delta(x) \psi dx = E\int_{-\epsilon}^{\epsilon} \psi dx\]

좌변과 우변의 \(\epsilon\)를 0으로 보내면, \(\psi\)는 연속이므로 우변은 0이다.

\[= - \frac{\hbar^2}{2m} \int_{-0^-}^{0^+}\frac{d}{dx} d\psi - \alpha \psi(0)\] \[=- \frac{\hbar^2}{2m} \left[ \frac{d\psi}{dx} \right]^{0^+}_{-0^-} - \alpha \psi(0)\] \[= - \frac{\hbar^2}{2m} \left( \frac{d\psi}{dx}(0^+) - \frac{d\psi}{dx}(0^-) \right) = \alpha \psi(0)\] \[\implies \psi_{2}'(0) - \psi_{1}'(0) = -\frac{2m\alpha}{\hbar^2} \psi_{1}(0)\]

\(\frac{d\psi}{dx}\)는 \(x=0\)에서 불연속인데, 그 차이는 \(- \frac{2m\alpha}{\hbar} \psi_{1}(0)\)과 같다. \(\psi_{1}(0)=\psi_{2}(0)\)이므로, \(\psi_{1}\) 대신 \(\psi_{2}\)를 사용해도 무방하다. 이 Boundry Condition 2개를 기억하자.

\[\psi_{1}(0) = \psi_{2}(0)\] \[\psi_{2}'(0) - \psi_{1}'(0) = -\frac{2m\alpha}{\hbar^2} \psi_{1}(0)\]

(1) Bound State : \(E<0\)

\[- \frac{\hbar^2}{2m} \frac{d^2}{dx^2} \psi = E \psi\] \[\frac{d^2 \psi}{dx^2} = - \frac{2mE}{\hbar^2} \psi\]

Let. \(\kappa^2 \equiv - \frac{2mE}{\hbar^2}\).

\[\frac{d^2 \psi}{dx^2} = \kappa^2 \psi\]

\(\psi\)는 다음과 같다.

\[\psi(x) = Ae^{\kappa x} + Be^{-\kappa x}\]

구역 1과 구역 2는 서로 Bound Condition이 다르므로, 각각 따로 해석해야 한다.

\[\psi_{1}(x) = Ae^{\kappa x} + Be^{-\kappa x}\] \[\psi_{2}(x) = Fe^{\kappa x} + Ge^{-\kappa x}\]

\(\psi_{1}\)은 \(x=-\infty\)일 때 발산하면 안된다. 따라서 \(B=0\)이다. 같은 논리로, \(F=0\)이어야 한다. \(\psi\)는 항상 연속이다. 따라서 \(x=0\)에서도 연속이어야 한다. psi 제곱은 확률 밀도함수이고, 확률 밀도함수는 반드시 연속이어야 하기 때문이다.

\[\psi_{1}(0^-) = \psi_{2}(0^+) \implies A = G\]

따라서 다음과 같다.

\[\psi_{1}(x) = Ae^{\kappa x}\] \[\psi_{2}(x) = Ae^{-\kappa x}\]

정규화 하면 \(A\)를 찾을 수 있다. \(\psi_{1}\)과 \(\psi_{2}\)는 대칭이므로, 둘 중 아무거나 계산해 \(\frac{1}{2}\)과 같다고 두면 된다.

\[\frac{1}{2} = \int_{0}^{\infty}\lvert \psi_{2} \rvert^2dx = \int_{0}^{\infty} \lvert A \rvert^2 e^{- 2 \kappa x} dx\] \[= \lvert A \rvert^2 \left[ - \frac{1}{2 \kappa} e^{-2 \kappa x} \right]^\infty_{0} = \lvert A \rvert^2 \cdot \frac{1}{2 \kappa}\] \[\implies A = \sqrt{ \kappa }\] \[\therefore ~~ \psi_{1}(x) = \sqrt{ \kappa } e^{\kappa x}, ~~ \psi_{2}(x) = \sqrt{ \kappa } e^{-\kappa x}\]

이제 구속되었을 때 어떤 에너지(\(E\))를 갖는지만 구하면 된다. 에너지는 \(\kappa\)를 구하면 된다. 이것을 구하기 위해, 두번째 Boundry Condition을 사용하자.

\[\psi_{2}'(0) - \psi_{1}'(0) = - \frac{2m\alpha}{\hbar^2}\psi_{1}(0)\] \[\implies - \kappa \sqrt{ \kappa } e^{-\kappa x}\mid_{x=0} - \kappa \sqrt{ \kappa } e^{\kappa x}\mid_{x=0} = - \frac{2m \alpha}{\hbar^2} \sqrt{ \kappa }e^{\kappa x}\mid_{x=0}\] \[\implies - 2 \kappa = - \frac{2m\alpha}{\hbar^2} \implies \kappa = \frac{m\alpha}{\hbar^2}\]

따라서 구속된다면, 양자계가 갖는 에너지는 다음과 같다

\[E= - \frac{\kappa^2 \hbar^2}{2m} = - \frac{\hbar^2}{2m} \left( \frac{m \alpha}{\hbar^2} \right)^2 = - \frac{m\alpha^2}{2\hbar^2}\]

가질 수 있는 에너지가 상수다. 따라서, 구속된다면 하나의 상태만 가질 수 있다. 그때 갖는 에너지는 위와 같고, 파동 함수는 \(x=0\)에서 표쪽한 모양을 가진다.

\[\psi(x) = \sqrt{ \kappa }e^{-\kappa \lvert x \rvert }\]

(2) Scattering State : \(E>0\)

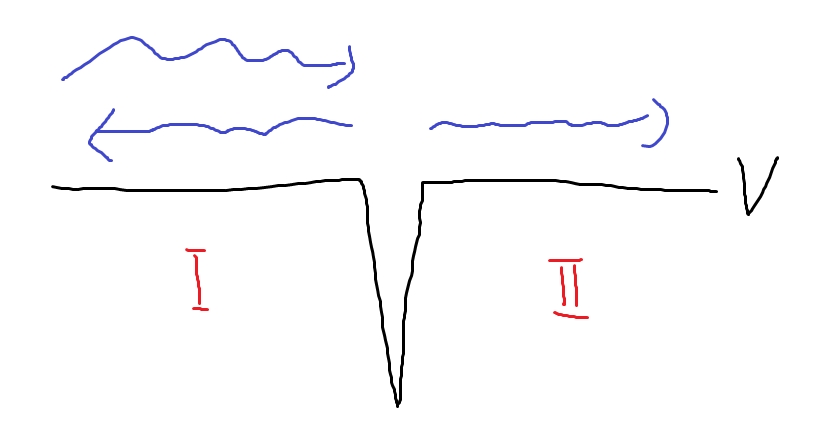
상황은 위와 같다. 사실, 고전역학 문제라면 에너지 \(E\)를 갖는 입자는 충돌하지 않고 그냥 지나갈 것이다. 하지만 양자역학은 다르다. 충돌할 확률이 존재한다. 왜? 파동이니까. 파동이 충돌하면 일부는 반사하고, 일부는 투과된다. 따라서 두개의 파동으로 나뉘는데, 각각 반사파와 투과파가 그것이다.

이 정보를 갖고 슈뢰딩거 방정식을 풀어보자. 아까와 같이 구역 1, 2를 나눠서 각각의 해를 구한다.

\[- \frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} = E \psi \implies \frac{d^2\psi}{dx^2} = -\frac{2mE}{\hbar^2} \psi\]

\(E>0\)이므로, 다음 값을 \(k\)로 정의한다.

\[k^2 \equiv \frac{2mE}{\hbar^2}\] \[\implies \frac{d^2\psi}{dx^2}= - k^2 \psi\] \[\therefore ~~ \psi_{1}(x) = Ae^{ikx} + Be^{-ikx}\] \[\therefore ~~ \psi_{2}(x) = Fe^{ikx} + Ge^{-ikx}\]

여기에 시간 요소 \(e^{-iEt / \hbar}\)를 결합한다고 생각해보라. \(e^{ikx}\) 항은 \(e^{i(kx - (E/\hbar) t)}\)가 되어 오른쪽으로 움직이는 파동을 의미하게 된다. \(e^{-ikx}\)항은 반대로 왼쪽으로 움직이는 파동을 의미하게 된다. 우리는 왼쪽에서 오다가 부딪히는 파동만을 생각한다고 약속하자. 그 반대의 상황은 대칭적이므로, 바라보는 방향만 뒤집으면 같은 상황으로 만들 수 있다.

그렇다면, \(A\)는 입사파의 진폭이다. \(B\)는 반사파의 진폭이며, \(F\)는 투과파의 진폭이다. \(G\)는 존재하지 않는다. 구역 2에서 오른쪽에서 왼쪽으로 오는 파동은 없기 때문이다.

\[G=0\]

이제 Boundry Condition을 사용하자.

\[\psi_{1}(0) = \psi_{2}(0) \implies A + B = F\] \[\psi_{2}'(0) - \psi'_{1}(0) = - \frac{2m\alpha}{\hbar^2} \psi_{1 |\mid 2}(x)\] \[\implies ikF - (ikA - ikB) = - \frac{2m\alpha}{\hbar^2} F\] \[\implies F - A + B = i \frac{2m\alpha}{k\hbar^2}F\]

목표가 무엇인가? 입사파의 진폭 \(A\)로 각각 반사파와 투과파의 진폭을 표현할 수 있으면 좋지 않을까? 이 목표를 갖고 두 식을 연립한다.

\[A + B - A + B = i \frac{2m\alpha}{k\hbar^2}F\] \[\implies B = i \frac{m\alpha}{k\hbar^2}F\]

편의를 위해 다음 상수를 정의한다.

\[\beta \equiv \frac{m\alpha}{k\hbar^2}\] \[B = i \beta F\]

1번 식에 대입한다.

\[A + i \beta F = F \implies A = (1-i\beta)F\] \[\therefore ~~ F = \frac{1}{1-i\beta}A\]

\(F=\frac{1}{i\beta}B\) 관계를 위 식에 대입한다.

\[\therefore ~~ B = \frac{i\beta}{1-i\beta}A\]

각 계수 \(A,B,F\)는 파동의 진폭이면서, 동시에 (제곱하면)각 상태가 가질 확률 을 의미하기도 한다. \(A\) 확률에 대한 \(B, F\) 상태의 확률의 비를 정의해보자.

\[R\equiv\frac{\lvert B \rvert^2}{\lvert A \rvert^2 }\] \[= \frac{B^*B}{\lvert A \rvert^2 } = \left( \frac{i\beta}{1-i\beta} \right)^* \left( \frac{i\beta}{1-i\beta} \right) \frac{\lvert A \rvert^2}{\lvert A \rvert^2 }\] \[= \left( -\frac{i\beta}{1+i\beta} \right)\left( \frac{i\beta}{1-i\beta} \right) = \frac{\beta^2}{1+\beta^2}\]

위 \(R\)을 반사 계수라고 한다.

\[T\equiv \frac{\lvert F \rvert^2}{\lvert A \rvert^2 }\] \[= \frac{F^*F}{\lvert A \rvert^2 }=\left( \frac{1}{1+i\beta} \right)\left( \frac{1}{1-i\beta} \right) \frac{\lvert A \rvert^2}{\lvert A \rvert^2 }\] \[= \frac{1}{1+\beta^2}\]

\(T\)를 투과 계수라고 한다. 입사파가 충돌했을 때, 반사되고 투과되는 확률의 합은 자명하게 1이다.

\[R + T = \frac{\beta^2}{1+\beta^2} + \frac{1}{1+\beta^2} = \frac{1+\beta^2}{1+\beta^2}=1\]

\(\beta^2\)는 다음과 같다.

\[\beta = \frac{m\alpha}{k\hbar^2} = \frac{m\alpha}{\hbar^2} \cdot \frac{\hbar}{\sqrt{ 2mE }} = \sqrt{ \frac{m^2\alpha^2}{2mE \hbar^2} } = \sqrt{ \frac{m\alpha^2}{2\hbar^2E} }\] \[\beta^2 = \frac{m\alpha^2}{2\hbar^2E}\]

\(\beta\)는 \(E\)에 대한 함수이므로, \(R\)과 \(T\) 또한 \(E\)에 대한 함수로 나타낼 수 있다.

\[R= \frac{\beta^2}{1+\beta^2} = \frac{\frac{m\alpha^2}{2\hbar^2E}}{1+ \frac{m\alpha^2}{2\hbar^2E}} = \frac{\frac{m\alpha^2}{2\hbar^2E}}{\frac{2\hbar^2E + m\alpha^2}{2\hbar^2E}}= \frac{1}{1+(2\hbar^2E / m\alpha^2)}\] \[T = \frac{1}{1+\beta^2} = \frac{1}{1+ (m\alpha^2 / 2\hbar^2E)}\]

가지고 오는 에너지가 높을 수록 반사 확률은 작아지고, 투과 확률은 높아진다. 당연히 강한 에너지로 부딪히면 투과가 더 잘될 것이다. 반대로 약한 에너지를 가지고 오면, 반사될 확률이 올라간다. 만약 에너지가 매우 작아지면 어떻게 될까? \(E\to 0\)이면, \(\beta^2 \to \infty\)이며 \(T\to 0\), \(R \to 1\)이다. 이 경우 대부분이 반사된다.

하지만 우리는 규격화 상수 \(A\)를 구할 수 없었다. 사실 이는 당연하다. 파동이 퍼텐셜에 구속되지 않는 자유 입자이므로, 하나의 고유 상태를 가질 수 없기 때문이다. 하지만 우리가 분석할 수 있는 것은 무엇인가? 시스템에 들어오는 양자의 에너지 \(E\)를 알고 있으면, 반사 계수 \(R\)과 투과 계수 \(T\)를 구해 반사될 확률과 투과할 확률을 구할 수 있다는 것이다.

\[V=\alpha \delta(x)\]

만약 퍼텐셜이 위와 같으면 어떻게 될까? 퍼텐셜은 \(x=0\)에서 무한대의 장벽을 만든다. 고전 역학의 문제에선 무한대의 퍼텐셜 장벽을 절때 넘을 수 없다. 하지만 양자역학에선 다르다! 위 결과에서 \(\alpha \to -\alpha\)로 바꾸기만 하면 된다. 그런데 \(R\)과 \(T\)를 보라. \(\alpha\)가 제곱의 형태로 존재한다. 따라서 퍼텐셜이 장벽으로 바뀌어도, 반사될 확률과 투과될 확률이 같다! 장벽이 있는데 그것을 뚫고 입자가 투과할 확률이 존재한다? 이것을 흔히 양자 터널링 효과라고 부른다.