양자역학 17. 양자계가 퍼텐셜에 구속되는 기준이 무엇인가

양자계가 퍼텐셜에 구속속되거나, 구속되지 않는 기준이 무엇인가?

양자계가 퍼텐셜에 구속되면 상태가 양자화되고, 구속되지 않으면 연속적이다. 구속된다는 기준이 무엇일까까? 에너지를 갖고 있는 양자가 특정 퍼텐셜에 들어오는 상황을 상상하자. 두가지 시츄에이션이 생길 수 있다. (1) 양자가 퍼텐셜에 구속(bound) 되거나, (2) 그대로 튕겨져(scattering) 나가거나. 어떨 때 입자가 구속되고, 어떨 때 튕겨나갈까? 양자가 가진 \(E\)와 \(V\)를 잘 비교해보면 되지 않을까?

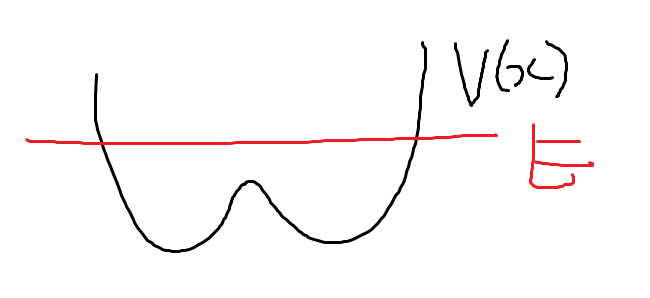
고전계를 상상해보자. 만약 퍼텐셜이 위 그림과 같고, 에너지가 \(E\)일 때 퍼텐셜 안으로 들어왔다? \(E\)만으론 \(V(x)\) 퍼텐셜을 벗어날 수 없으므로 반드시 구속된다. 에너지가 보존된다면, 총 에너지가 \(E\)인 양자는 퍼텐셜이 작아졌다 커졌다를 반복하게 된다.

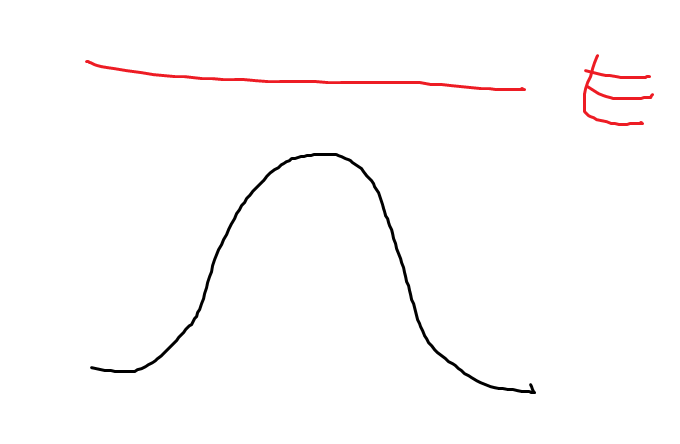
퍼텐셜이 위 그림과 같이 생겼다면, 구속되지 않는다. 입자는 퍼텐셜 에너지가 작아지는 방향으로 이동하면서, 감소하는 퍼텐셜 에너지가 운동 에너지로 전환되며 빠른 속도를 갖게 된다.

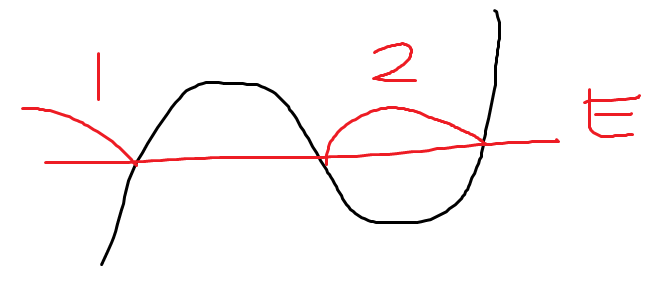
위 상황을 생각해보자. 이 경우는, 입자가 들어온 위치가 중요하다. 1번 영역에 입자가 들어왔다면, 구속되지 않는다. 2번 영역에 입자가 들어왔다면, 구속될 것이다. 같은 에너지인데도 들어온 위치에 따라 구속되거나 구속되지 않음이 결정될 수도 있다.

구속될지, 튕겨져 나갈지의 여부는 \(V\)의 모양, \(E\) 뿐만 아니라 위치에도 의존한다. 따라서 일반적인 기준을 생각하기가 어렵다. 하지만, 퍼텐셜이 \(x=\pm \infty\)일 때 에너지보다 크다면, 반드시 구속되지 않을까? 반대로 에너지보다 작다면, 구속되지 않을 확률이 크지 않을까?

\[E < V(-\infty) ~\cap~ E<V(\infty)\]

위 상황을 속박 상황으로 간주하자.

\[E>V(-\infty) ~ \cap ~ E>V(\infty)\]

위 상황을 충돌 상황으로 간주하자.

대부분의 포텐셜은 \(x=\pm 0\)일 때 0으로 간다. 따라서, 더 간단히 쓸 수 있다.

\[E < 0 \implies \text{속박 상태}\] \[E > 0 \implies \text{충돌 상태}\]

위 기준을 사용하면 입자가 속박될지, 충돌할지 예측정도는 해볼 수 있을 것 같다. 과연 양자계도 고전계와 비슷할까? 퍼텐셜이 디렉 델타함수일 때 결과를 분석해보자.