양자역학 10. 양자계의 조화 진동자가 무엇인가

양자계에서의 조화 진동자란 무엇인가?

기본적으로 조화 진동자의 포텐셜은 다음과 같다.

\[V(x) = \frac{1}{2} kx^2 = \frac{1}{2} m \omega^2 x^2\] \[\omega \equiv \sqrt{ \frac{k}{m} }\]

위 포텐셜을 슈뢰딩거 방정식에 넣고 풀면 된다. 풀이 방법은 사다리 연산자를 사용한 대수적인 방법과, 멱급수를 사용한 해석적인 방법이 있다. 풀어보기 전에, 왜 조화 진동자를 배우는가?

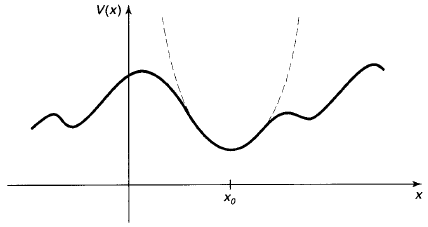
Local 극솟값에서, 양자계의 에너지가 그리 크지 않아 극댓값을 넘어갈 수 없다면 단순 조화에 가까운 운동을 하기 때문이다. 이를 해석적으로 증명해보면, Local 극솟값의 위치를 \(x_{0}\)라고 하자. \(x_{0}\)에서 테일러 전개하면

\[V(x) = V(x_{0}) + V'(x)\mid_{x=x_{0}} (x-x_{0}) + \frac{1}{2}V''(x)\mid_{x=x_{0}}(x-x_{0})+\dots\]

이고, 퍼텐셜은 상수만큼의 차이는 무의미하므로 \(V(x_{0})\)는 무시한다. \(V'(x_{0})=0\)이므로

\[V(x) \simeq \frac{1}{2}V''(x)\mid_{x=x_{0}}(x-x_{0})\]

로 근사할 수 있다. 이는 용수철상수가 \(k=V''(x_{0})\)인 단순 조화 운동이다.

(1) 사다리 연산자를 사용하여 슈뢰딩거 방정식 풀이 Time-indenpendent 슈뢰딩거 방정식에 \(V(x)=\frac{1}{2}m\omega^2 x^2\)를 대입한다.

\[- \frac{\hbar^2}{2m} \frac{d^2 \psi}{dx^2} + \frac{1}{2}m \omega^2x^2 \psi = E \psi\] \[\implies \frac{1}{2m}\left[ -\hbar^2 \frac{d^2}{dx^2} + (m\omega x)^2 \right]\psi = \frac{1}{2m} \left[ \left( -i\hbar \frac{d}{dx} \right)^2 + (mwx)^2 \right]\psi\] \[= \frac{1}{2m}[\hat{p}^2 + (m\omega x)^2]\psi = \hat{H}\psi\] \[\implies \hat{H} = \frac{1}{2m}[\hat{p}^2 + (m\omega x)^2]\]

이를 정리하기 위해 \(u^2+v^2 = (iu+v)(-iu+v)\)로 인수분해 하면 참 좋겠지만, 연산자는 교환법칙이 적용되지 않기 때문에 위 공식에서 \(iuv - viu\)가 상쇄되지 않는다. 따라서 다른 방법을 찾아야 한다. 사다리 연산자 (Ladder operator) \(\hat{a}_{\pm}\)를 정의해보자.

\[\hat{a}\pm=\frac{1}{\sqrt{ 2\hbar m\omega }}(\mp i\hat{p} + m\omega x)\]

두 사다리 연산자 \(\hat{a}_{+}\hat{a}_{-}\)와 \(\hat{a}_{-}\hat{a}_{+}\)를 곱해보자.

\[\hat{a}_{+}\hat{a}_{-} = \frac{1}{2\hbar m\omega}(-i\hat{p} + m\omega x)(i\hat{p} + m\omega x)\] \[= \frac{1}{2\hbar m\omega}(\hat{p}^2 - i\hat{p} m\omega x + m\omega x i\hat{p} + (m\omega x)^2)\] \[= \frac{1}{2\hbar m\omega}(\hat{p}^2 + (m\omega x)^2 + im\omega(x\hat{p} - \hat{p}x))\]

이때 \(x\hat{p} - \hat{p}x\)는 \(x\)와 \(\hat{p}\)의 Commucator \([x,\hat{p}]\)과 같고 그 값은 \(i\hbar\)이다.

\[[x,\hat{p}] = i\hbar\] \[= \frac{1}{2\hbar m\omega}(\hat{p}^2 + (m\omega x)^2 - \hbar m\omega)\] \[= \frac{1}{2\hbar m\omega}(\hat{p}^2 + (m\omega x^2)) - \frac{1}{2}= \frac{1}{\hbar \omega} \hat{H} - \frac{1}{2}\] \[\implies \hat{H} = \hbar \omega\left( \hat{a}_{+}\hat{a}_{-} + \frac{1}{2} \right)\]

이 연산을 \(\hat{a}_{-}\hat{a}_{+}\)에 대해서도 하면 다음 결과를 얻는다.

\[\hat{H} = \hbar \omega\left( \hat{a}_{-}\hat{a}_{+} - \frac{1}{2} \right)\] \[\therefore ~~ \hat{H} = \hbar \omega\left( \hat{a}_{\pm}\hat{a}_{\mp} \pm \frac{1}{2} \right)\]

이 결과를 슈뢰딩거 방정식 \(\hat{H} \psi = E \psi\)에 넣어보자.

\[\hbar \omega\left( \hat{a}_{\pm}\hat{a}_{\mp} \pm \frac{1}{2} \right)\psi = E\psi\]

그래서, 도대체 레더 오퍼레이터 \(\hat{a}_{\pm}\)는 뭐하는 자식인가? \(\hat{H}(\hat{a}_{+}\psi)\)를 계산해보면 그 의미를 알 수 있다.

\[\hat{H} (\hat{a}_{+}\psi)=\hbar \omega\left( \hat{a}_{+}\hat{a}_{-} + \frac{1}{2} \right)(\hat{a}_{+}\psi)\] \[= \hbar \omega\left( \hat{a}_{+}\hat{a}_{-}\hat{a}_{+} \psi + \frac{1}{2} \hat{a}_{+} \psi\right)\] \[= \hbar \omega\left( \hat{a}_{+}\hat{a}_{-}\hat{a}_{+} + \hat{a}_{+}\left( \frac{1}{2} \right) \right) \psi\] \[= \hbar \omega \hat{a}_{+}\left( \hat{a}_{-}\hat{a}_{+} + \frac{1}{2} \right)\psi\]

\([\hat{a}_{-},\hat{a}_{+}] = 1 \implies \hat{a}_{-}\hat{a}_{+}=1+\hat{a}_{+}\hat{a}_{_{-}}\)이므로

\[=\hbar \omega \hat{a}_{+}\left( 1+\hat{a}_{+}\hat{a}_{-}+\frac{1}{2} \right)\psi\] \[= \hat{a}_{+}(\hbar \omega + \hat{H})\psi = \hat{a}_{+}(\hbar \omega + E)\psi\] \[= (\hbar \omega + E)\hat{a}_{+}\psi\] \[\therefore ~ \hat{H}(\hat{a}_{+}\psi) = (\hbar \omega + E)\hat{a}_{+} \psi\]

즉, \(\hat{a}_{+}\psi\)를 이렇게 해석해볼 수 있다.

\[\psi \text{ 상태의 에너지가 } E\text{ 일 때, 그보다 한칸 위의 에너지 상태는 } \hbar w+E\text{ 이며, 상태는 } \hat{a}_{+}\psi \text{와 같다.}\]

\(\hat{a}_{-}\psi\)는 \(\psi\)보다 에너지 상태를 한단계 낮추는 것과 같다.

즉, \(\psi_{0}\)을 구해서 \(\hat{a}_{+}\)를 계속 적용하면 \(\psi_{n}\)을 구할 수 있다.

\[\psi_{n} = A_{n}(\hat{a}_{+})^n\psi_{0}\]

이때 \(A_{n}\)은 정규화를 위한 상수이다. 에너지 \(E_{n}\)도 슈뢰딩거 방정식으로 구할 수 있다.

\[\hat{H} \psi_{0} = E_{0} \psi_{0}\] \[\implies \hbar \omega\left( \hat{a}_{+} \hat{a}_{-} + \frac{1}{2} \right) \psi_{0} = E_{0} \psi_{0}\] \[= h\omega \hat{a}_{+}\hat{a}_{-} \psi_{0} + \frac{1}{2}\hbar \omega \psi_{0} = E_{0}\psi_{0}\]

\(\hat{a}_{-}\psi_{0} = 0\)이므로 다음과 같다.

\[E_{0} = \frac{1}{2} \hbar \omega\] \[E_{n} = \frac{1}{2} \hbar \omega + n \hbar \omega = \left( n + \frac{1}{2} \right)\hbar \omega\]

[!tip] Number Operator의 정의{title} \(E_{n}\)에 대한 슈뢰딩거 방정식은 다음과 같다.

\[\hat{H} \psi_{n} = E_{n} \psi_{n}\] \[\implies \hbar \omega \left( \hat{a}_{+}\hat{a}_{-} + \frac{1}{2} \right)\psi_{n} = E_{n} \psi_{n} = \hbar \omega\left( n + \frac{1}{2} \right) \psi_{n}\] \[\therefore ~~ \hat{a}_{+}\hat{a}_{-} = n\]

\(\psi_{0}\)를 어떻게 구할까? \(\psi_{0}\)는 Ground state, \(\psi_{n}~(n\neq 0)\)은 Excited state라고 한다. 양자계에서 Ground state의 Energy는 절대 0이 될 수 없다. 그 이유는 불확정성 원리 때문이다. 위치와 속도를 정확히 알 수 없다는 것은, 계속 움직인다는 뜻이고, 움직이면 에너지가 존재하기 때문이다.

\(\hat{a}_{-}\psi_{0}=0\)임을 이용하자.

\[\hat{a}_{-}\psi_{0} = 0 \implies \frac{1}{\sqrt{ 2\hbar m\omega }}(i\hat{p} + m\omega x)\psi_{0}\] \[\frac{1}{\sqrt{ 2\hbar m\omega }} \left( \hbar \frac{d}{dx} + m\omega x \right)\psi_{0} = 0\] \[\implies \frac{d\psi_{0}}{dx} = -\frac{m\omega}{\hbar}x\psi_{0}\] \[\psi_{0}(x) = A e^{-(m\omega / 2\hbar)x^2}\]

구한 해를 정규화하여 계수를 찾아보자.

\[1=\int_{-\infty}^{\infty}\lvert \psi_{0} \rvert^2dx = \int_{-\infty}^{\infty}(Ae^{-(m\omega / 2\hbar)x^2})^2dx\] \[= A^2 \int_{-\infty}^{\infty} e^{-(m\omega / \hbar) x^2} dx = A^2 \sqrt{ \frac{\hbar \pi}{m\omega} }\] \[\implies A = \left( \frac{m\omega}{\hbar \pi} \right)^{1/4}\]

결론은 다음과 같다.

\[\psi_{0}(x) = \left( \frac{m\omega}{\hbar\pi} \right)^{1/4} e^{-(m \omega / 2 \hbar)x^2}\]

\(A_{n}\)은 어떻게 구하는가?

\[\psi_{n} = A_{n} (\hat{a}_{+})^n \psi_{0}\]

에 있었던 정규화를 위한 계수 \(A_{n}\)을 구해보자. 우선, \(\hat{a}_{\pm}\)의 에르미트 켤레는 \(\hat{a}_{\mp}\)와 같으므로, 에르미트 켤레 정의에 의해 다음 사실이 만족한다는 것을 알고 있어야 한다.

\[\langle f, \hat{a}_{\pm}g \rangle = \langle \hat{a}_{\mp}f, g \rangle\] \[\implies \int_{-\infty}^{\infty}f^* \hat{a}_{\pm}g dx = \int_{-\infty}^{\infty} (\hat{a}_{\mp}f)^* g dx\]

\(A_{n}\)을 알기 위해 그냥 \(\psi_{n}\)에다 사다리 연산자를 적용하면 어떤 결과가 나올지 안다면, 그 사실을 통해 \(A_{n}\)을 구할 수 있을 것 같다.

\[\hat{a}_{+} \psi_{n} = \alpha_{n} \psi_{n+1}\] \[\hat{a}_{-}\psi_{n} = \beta_{n}\psi_{n-1}\]

사실 결론은 다음과 같다. 아래 사실은 정말 중요하기 때문에 암기하라.

\[\hat{a}_{+}\psi_{n} = \sqrt{ n+1 } \psi_{n+1}\] \[\hat{a}_{-} \psi_{n} = \sqrt{ n } \psi_{n-1}\]

[!NOTE]- 유도 과정{title} \(\hat{a}_{+}\psi_{n}\)의 의미는 에너지가 \(n+1\)인 상태와 같다. \(\alpha_{n}\)은 정규화 상수다. 따라서 \(\hat{a}_{+}\psi_{n}\)을 정규화 해보자.

\[1=\int_{-\infty}^{\infty} (\hat{a}_{+}\psi_{n})^* (\hat{a}_{+}\psi_{n})dx = \int_{-\infty}^{\infty}(\alpha_{n}\psi_{n+1})^*(\alpha_{n}\psi_{n+1})dx= \lvert \alpha_{n} \rvert^2\]

\(\int_{-\infty}^{\infty}f^* \hat{a}_{\pm}g dx = \int_{-\infty}^{\infty} (\hat{a}_{\mp}f)^* g dx\) 임을 이용한다.

\[= \int_{-\infty}^{\infty} (\hat{a}_{-}\hat{a}_{+}\psi_{n})^* \psi_{n}dx\]

\(\hat{a}_{-}\hat{a}_{+}\)는 \([\hat{a}_{-},\hat{a}_{+}]=1\) 관계에 의해 \(\hat{a}_{-}\hat{a}_{+} = \hat{a}_{+}\hat{a}_{-}+1\)이다.

\(= \int_{-\infty}^{\infty}(\hat{a}_{+}\hat{a}_{-}+1)\psi_{n}^* \psi_{n} dx\) \(\hat{a}_{+}\hat{a}_{-}\)는 Number Operator임을 이용한다.

\[\hat{a}_{+}\hat{a}_{-}\psi_{n} = n \psi_{n}\] \[\hat{N} \equiv \hat{a}_{+}\hat{a}_{-}=n\]

따라서 다음과 같다.

\[(n+1)\int_{-\infty}^{\infty}\psi_{n}^*\psi_{n}dx = n+1\] \[\therefore ~ \alpha_{n} = \sqrt{ n+1 }\] \[\therefore ~ \hat{a}_{+} \psi_{n} = \sqrt{ n+1 }\psi_{n+1}\]

\(\beta_{n}\) 또한 똑같이 유도할 수 있다.

\[1=\int_{-\infty}^{\infty}(\hat{a}_{-} \psi_{n})^* (\hat{a}_{-} \psi_{n}) dx = \lvert \beta_{n} \rvert^2\] \[= \int_{-\infty}^{\infty} (\hat{a}_{+}\hat{a}_{-}\psi_{n})^* \psi_{n}dx\] \[= n\int_{-\infty}^{\infty}\psi_{n}^* \psi_{n}dx = n\] \[\therefore ~ \beta_{n} = \sqrt{ n }\] \[\therefore ~ \hat{a}_{-}\psi_{n} = \sqrt{ n } \psi_{n-1}\]

\(A_{n}\)은 \(\psi_{n+1}=\frac{1}{\sqrt{ n+1 }} (\hat{a}_{+})^n \psi_{0}\)에 \(n=1\)부터 계속 넣어보면 쉽게 구할 수 있다.

\[\psi_{1} = \frac{1}{\sqrt{ 2 }} \hat{a}_{+} \psi_{0}\] \[\psi_{2} = \frac{1}{\sqrt{ 3 }} \hat{a}_{+} \psi_{1} = \frac{1}{\sqrt{ 3 }} \frac{1}{\sqrt{ 2 }} (\hat{a}_{+})^2 \psi_{0}\] \[\psi_{3} = \frac{1}{\sqrt{ 4 }} \hat{a}_{+} \psi_{2} = \frac{1}{\sqrt{ 4 }} \frac{1}{\sqrt{ 3 }} \frac{1}{\sqrt{ 2 }} (\hat{a}_{+})^3 \psi_{0}\] \[\dots\] \[\psi_{n} = \frac{1}{\sqrt{ n! }} (\hat{a}_{+})^n \psi_{0}\]

규격화 상수 \(A_{n}\)은 \(\frac{1}{\sqrt{ n! }}\)이다.

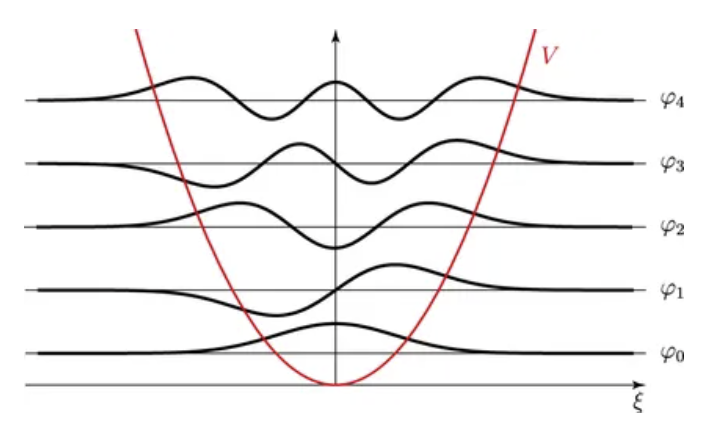
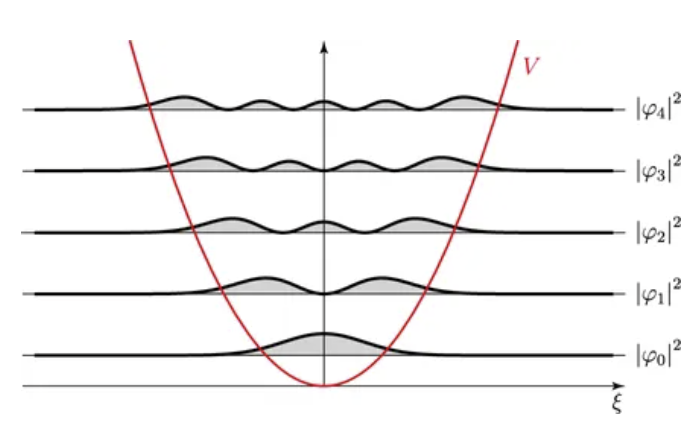
(2) 멱급수를 이용한 풀이는… 생략 위에서 구한 \(\psi(x)\) 해는 수학적으로 완벽한 해는 아니다. 멱급수를 사용해서 슈뢰딩거 방정식을 풀면 다음과 같다. 암기할 필요는 없다.

\[\psi_{n}(x) = \left( \frac{m\omega}{\pi \hbar} \right)^{1/4} \frac{1}{\sqrt{ 2^n n! }} H_{n}(\xi)e^{- \xi^2 / 2}\] \[\xi \equiv \sqrt{ \frac{m \omega}{\hbar} }x\]

\(\xi\)는 무차원 변수를 표기할 때 많이 사용한다.

[!tip] \(\langle V \rangle\)을 편하게 계산하는 방법{title}

\[\hat{a}_{\pm} = \frac{1}{\sqrt{ 2\hbar m\omega }} (\mp i\hat{p} + m\omega x)\]

의 식을 더하거나 빼면 \(x, \hat{p}\)에 대한 식을 사다리연산자로 표현할 수 있다.

\[x = \sqrt{ \frac{\hbar}{2m\omega} } (\hat{a}_{+} + \hat{a}_{-})\] \[\hat{p} = i \sqrt{ \frac{\hbar m\omega}{2} }(\hat{a}_{+} - \hat{a}_{-})\]

예를들어 \(\langle V \rangle\)를 계산한다고 해보자.

\[\langle V \rangle = \int_{-\infty}^{\infty} \psi_{n}^* \left( \frac{1}{2}m\omega^2 x^2 \right) \psi_{n} dx\] \[= \int_{-\infty}^{\infty} \psi_{n}^* \left( \frac{1}{2}m\omega^2 \left( \sqrt{ \frac{\hbar}{2m\omega} } (\hat{a}_{+} + \hat{a}_{-}) \right)^2 \right) \psi_{n} dx\] \[= \frac{\hbar \omega}{4} \int_{-\infty}^{\infty} \psi_{n}^* ( \hat{a}_{+}^2 + \hat{a}_{+}\hat{a}_{-} + \hat{a}_{-}\hat{a}_{+} + \hat{a}_{-}^2 ) \psi_{n} dx\]

\(\hat{a}_{+}^2 \psi_{n}\)과 \(\hat{a}_{-}^2\psi_{n}\)은 \(\psi_{n}\)과 정규직교관계이므로, 적분하면 0이다. \(\hat{a}_{-}\hat{a}_{+} = 1+\hat{a}_{+}\hat{a}_{-}\)로 바꾸고, \(\hat{a}_{+}\hat{a}_{-} = n\)임을 이용한다.

\[= \frac{\hbar \omega}{4} \int_{-\infty}^{\infty} \psi_{n}^* (2 n + 1) \psi_{n} dx\] \[=\frac{1}{2} \hbar \omega \left( n + \frac{1}{2} \right)\]

위 방법을 통해 n번째 정상상태 (\(\psi_{n}\))에 대해 \(\langle x \rangle, \langle p \rangle, \langle x^2 \rangle, \langle p^2 \rangle, \langle T \rangle\)을 계산해보면 다음과 같다.

\[\langle x \rangle = 0\] \[\langle p \rangle = 0\] \[\langle x^2 \rangle = \frac{\hbar}{m\omega} \left( n + \frac{1}{2} \right)\] \[\langle p^2 \rangle = \hbar m \omega \left( n + \frac{1}{2} \right)\] \[\langle T \rangle = \frac{1}{2} \hbar \omega \left( n + \frac{1}{2} \right)\] \[\langle H \rangle = \langle T \rangle + \langle V \rangle = \frac{1}{2} \hbar \omega\left( n + \frac{1}{2} \right) + \frac{1}{2} \hbar \omega \left( n + \frac{1}{2} \right) = \hbar \omega \left( n + \frac{1}{2} \right) = E_{n}\]

무한 퍼텐셜 우물과 조화 진동자의 차이

무한 퍼텐셜 우물은 에너지가 \(E_{n} \propto n^2\)에 비례하고, 조화 진동자는 \(E_{n} \propto n\)에 비례한다. 이런 차이가 나는 이유를 우리는 어떻게 받아들여야 할까?

무한 퍼텐셜 우물

조화 진동자

무한 퍼텐셜 우물은 벽 밖에서 관측될 확률이 0이고, 완전히 갇혀있다. 따라서 좁은 곳에 파장을 많이 우겨넣을 수록 파장이 위로 커지게 된다. 따라서 에너지가 \(n^2\)라는 높은 수에 비례한다.

조화 진동자는 제한된 퍼텐셜 밖에서 관측될 확률이 존재한다. 이게 무슨 말이냐면, 벽으로 막아놨더니 벽 뒤에서 입자가 관측될 확률이 0이 아니란 뜻이다. 이를 양자 터널링 현상이라고 부른다. 구속도 좀 널널하고, 퍼텐셜도 에너지가 커질 수록 더 넓어진다. 따라서, 에너지가 \(n\)에 비례해도 괜찮다.