알고리즘 7. Randomized Algorithm

건국대학교 알고리즘 김성열 교수님의 수업을 정리한 내용입니다.

Randomized Algorithm

Las Vegas Monte Carlo

• 랜더마이즈 알고리즘
  • 알고리즘을 수행하는 과정에서 난수를 활용하는 알고리즘이다. 예를 들어 퀵 소트의 피벗을 랜덤하게 선택하도록 하면, 특정 상황에 최악의 경우를 내던 알고리즘이 평균적으로 잘 동작하도록 만들 수 있다. 라스 베가스 알고리즘과 몬테 카를로 알고리즘 두 유형으로 구분한다.
  • 라스 베가스
    • 항상 정답을 내놓지만, 수행 시간이 달라질 수 있다.
  • 몬테 카를로
    • 가끔 오답을 내놓지만, 수행 시간이 일정하다.
  • 라스 베가스 알고리즘과 몬테 카를로 알고리즘은 서로 변환이 가능하다. 그냥 특정 수행 시간을 정해두고, 특정 수행 시간을 넘어가면 끊고 답을 내버리면 라스 베가스에서 몬테 카를로가 된다. 만약 정답인지 아닌지 확인할 수 있다면, 정답이 나올 때까지 몬테 카를로 알고리즘을 돌리면 라스 베가스 알고리즘이 된다.
  • 정렬된 Linked List에서 빠르게 값 X를 찾는 방법 (라스 베거스)
    • 전체 원소 n개 중 \(n^{1/2}\)개를 랜덤으로 뽑는다. 이후 X보다 작은 값 중 가장 큰 값 Y라고 하자. Y를 찾는데 걸리는 시간이\(O(n^{1/2})\)이고, 이후 한칸한칸 걸어가면서 탐색하면 최종적으로 \(O(n)\)이던 Search를 \(O(n^{1/2})\) 시간으로 개선한다.
    • 최악의 경우 찾는 X가 맨 끝 값이고, 랜덤으로 선택된게 맨 앞에 몰려있으면 \(O(n-n^{1/2})\)니까 \(O(n)\) 시간이긴 하다.
    • 하지만 랜더마이즈 알고리즘은 최악의 경우보다 평균적인 시간을 따져서 최적화하겠다는 마인드를 가진다.
    • 평균적으로 균등하게 뽑는다고 가정하면, X와 Y 사이의 평균 거리는 \(\frac{n}{n^{1/2}}=n^{1/2}\)이다. 따라서 평균 시간은 대충 \(O\left( n^{1/2}+ n^{1/2} \right)=O(n^{1/2})\)와 같다.
    • 100% 정답을 보장하지만, 수행 시간이 얼마나 걸릴지는 선택되는 값에 따라 제각각이다.
  • 소수 판정 (몬테 카를로)
    • 어떤 수 n이 주어졌을 때, 그것이 소수인지 아닌지 판정하려면 1부터 n-1까지 다 나누어봐야 하므로 Pseudo Polynormial Algorithm. 느리다. 2부터 n-1까지 순서대로 나눠보면, 최악의 경우가 존재할 가능성이 있다. 따라서 랜덤하게 숫자를 뽑아서 체크해보면, 소수가 아닌 경우 평균적으로 빠르게 체크해볼 수있다. 하지만 결국 소수라면 n번 전부 체크되긴 한다.
    • 페르마의 소정리를 활용한다. \(a^\exists \mid 1 < a < n\)일 때, \(a^{n-1}\%n \neq 1\)인 경우 n은 확실하게 소수가 아니다. 하지만 \(a^{n-1}\%n = 1\)라고 해서 n이 소수인건 아니다.
    • 중복을 허용하지 않으면서 랜덤하게 k개의 a를 뽑고, k번 테스트를 해본다. 테스트를 전부 통과하면 그냥 소수라고 치고, 테스트를 하나라도 통과하지 못하면 소수가 반드시 아니다.
    • 시간 복잡도는 \(O(k\log^2n)\)이다. 왜냐면 \(a^{n-1}\%n\)을 계산하는 시간이 모듈러 제곱 뭐시깽이 해가지고 \(O(\log^2n)\)이 걸린다고 하며, k번 테스트를 하기 때문이다.
    • 100% 정확한 결과를 내진 않지만, 오판할 확률은 무시 가능한 수준이며 항상 빠른 결과를 보장하기 때문에 대충 타협하면 괜찮은 알고리즘이다.
  • LCA
  • Fast Find MST

Lowest Common Ancestor

• Tree의 두 노드 사이의 가장 빠른 공통 조상을 찾는 방법.
• Binary Lifting 기법을 사용한다. Binary Lifting은 Binary Search에서 아이디어를 착안한다. 절반씩 탐색 범위를 줄여가면 Search를 \(O(n)\)에서 \(O(\log n)\)으로 줄일 수 있다. 위에서부터 내려오는 Search가 가능하다면 Binary Search Tree를 사용하면 되지만, 아래에서부터 위로 Search하는 경우 Binary Lifting 기법을 적용하면 된다. Tree에서의 Binary Lifting 기법은, 현재 노드에서 \(2^j ~~(\text{for } 0 \leq j \le \log H,~ \text{H is height of tree})\), 위의 노드에 대한 정보를 사전에 미리 계산해둔다. Tree의 노드 번호를 i라고 하면, i번째 노드에서 시작하여 어떤 다른 노드를 Search하기 위해 미리 계산해둔 값으로 Binary 탐색이 가능하다. 그러면 Search 시간이 최악의 경우 \(O(n)\)에서 \(O(\log n)\)으로 줄어든다.
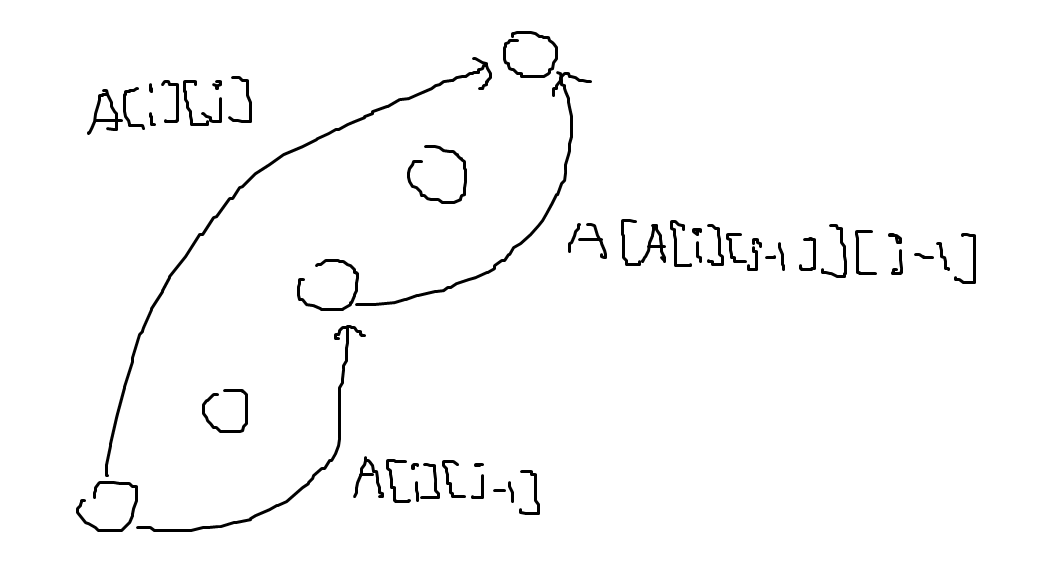
• \(A[i][j]\) Table을 정의한다. 이는 노드 i에서 \(2^j\) 위에 있는 조상 노드의 번호가 기록된다. 즉 \(A[i][0]\)은 i 노드의 Parent와 같다.
• 각 노드의 index number를 붙이기 위해 DFS를 돌려 pre number 또는 Post number를 붙인다. 이 경우 Pre number를 사용하자.
• \(A[i][j]\)를 구하기 위해서는 재귀적으로 \(A[i][j-1]\) 노드 번호의 \(2^{j-1}\) 위의 노드 번호를 구하면 된다.

• 따라서 점화식이 \(A[i][j]=A[A[i][j-1]][j-1]\)로 표현되며, \(A[i][0]\)을 모두 본인의 부모 노드를 기록하여 반복문으로 A 배열을 채움으로써 Preprocessing이 가능하다. 이 과정이 \(O(n\log n)\)이 걸린다. 그 이유는 i를 1부터 n까지 돌리고, j는 1부터 logn까지 돌리기 때문이다.
• 이 모든것을 활용하여 두 노드의 LCA를 구하는 과정은 다음과 같다.
  • Tree의 Pre Number, Depth Level, Binary Lifting Table (A Table)을 Pre Processing해둔다.
  • 두 노드가 주어졌을 때, 두 노드의 Level 정보를 확인하여 높이 차만큼 Level이 더 낮은 노드를 끌어 올려 두 노드의 Level을 맞춘다. 이때 두 노드를 a’, b라고 하자.
  • 초기 변수를 \(p=a'\), \(q=b\)로 설정하여 j를 logn부터 0까지 반복한다.
    • \(A[p][j] \neq A[q][j]\)면, \(p=A[p][j]\), \(q=A[q][j]\)로 설정하고 j를 하나 낮춘다.
    • \(A[p][j] = A[q][j]\)면, j만 하나 낮춘다.
    • 0까지 반복한다.
  • 반복이 끝나면, p와 q는 LCA의 바로 아래 노드가 된다.
  • \(A[p][j] = A[q][j]\)를 만족한다고 해서 바로 그 노드 번호가 LCA인것은 아니기 때문에, 가능한 모든 j의 경우를 체크해봐야 한다.
• LCA를 사용하면 Tree 내의 두 노드의 Shorest Path를 빠르게 찾을 수 있다. LCA를 구하면 \(O(\log n)\)만에 빠르게 찾을 수 있기 떄문이다.
• 더 빠른 알고리즘이 존재한다고 한다. Preprocessing이 \(O(n)\)만에 되고, LCA를 찾는 시간이 \(O(1)\)에 가능한 알고리즘이 있다.

Boruvka’s MST Algorithm

Randomized MST Algorithm

잘 모르겠다.

먼저 \(O(m\log n)\)에 찾는 방법은 Faster Find MST. 잘 쓰지는 않는다고 함. 그래프의 모든 Edge Weight가 다르다고 가정하자. 어떤 노드를 선택하고 인접한 엣지중 가장 Weight가 작은 것을 고른다. 그건 반드시 MST에 들어간다. 왜냐? 가장 작은 Edge가 없는 MST가 있다고 가정하자. 그 노드는 Tree에 들어가야 하기 떄문에 최소 Edge 엣지를 제외한 어떤 엣지 하나가 들어가야 한다. 하지만 그 Edge를 빼고 최소 Edge를 넣으면 더 좋은 MST가 만들어지기 때문에 모순이다.

그렇게 하면 연결된 노드 덩어리가 만들어짐. 이후 덩어리를 하나의 노드로 간주하고, 두 노드를 잇는 엣지중 Weight가 작은 Edge를 하나씩 고르면 된다. 노드당 최소 Edge를 고르기 위해 모든 Edge를 봐야하고, 그걸 모든 노드를 해야하므로 N+M이고 노드를 뭉탱이로 묶는것도 DFS 한번 돌리면 되므로 N+M. 그걸 총 logn번 해야한다? 왜? 그러면 \(O((n+m)\log n)=O(m\log n)\). 실제론 잘 안씀. 그래프를 새로 짜야해서 구현도 복잡하고 메모리도 많이 잡아먹기 때문에.

\(O(n+m)\)에 MST를 찾는 방법. Randomized MST.

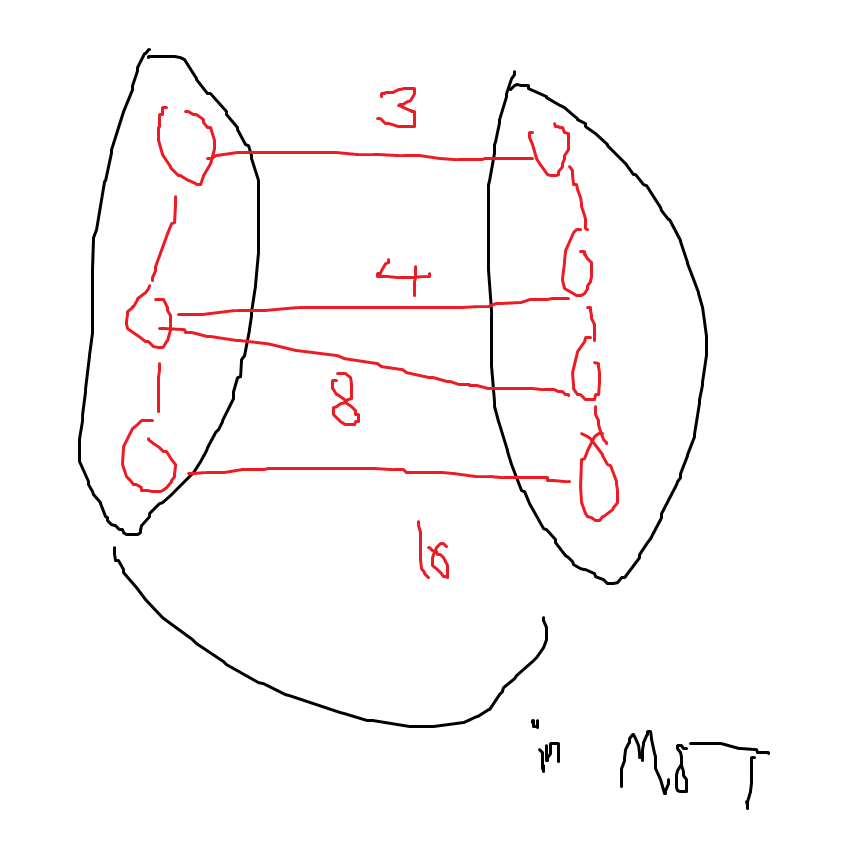
1. Boruvka Round를 3번 돌린다. (Boruvka Round가 무엇인가?, 왜 3번인가? 2번해도 되고 4번해도 된다고는 하는데 뒤의 내용이 좀 바뀐다. => (n, m) 사이즈의 그래프를 (n/8, m) 사이즈의 그래프를 만들려고 3번 돌린다고 한다.) 이때 C는 Contracted Edges. (한 라운드에서 뽑힌 뭉탱이 엣지, 압축된 엣지들?). 뽑은 애들은 무조건 MST에 들어가니까 뽑아두고 제외한다. 이 결과를 G’라고 한다.
2. G’에서 간선을 50% 확률로 랜덤하게 골라서 G’‘를 만든다. 그러면 사이즈는 \(\left( \frac{n}{8}, \frac{m}{2} \right)\)가 됨. (Forest가 뭐지? MSF는 MST에서 간선 몇개가 끊어진 것.)
3. 전체 알고리즘에 G’‘를 재귀적으로 넣으면 MSF가 나온다. 이를 F라고 하자.
4. F에서 Heavy Edge를 찾아 찾은 Heavy Edge를 G’에서 제거한다. 이를 G’'’라고 하자. Heavy Edge란 한 노드에서 연결된 엣지가 두개 있는데 그중 큰 엣지가 헤비 엣지다. 반대가 Light 엣지? Light 엣지는 답일 수도 있다? 무조건 답인거 아니야?
5. 
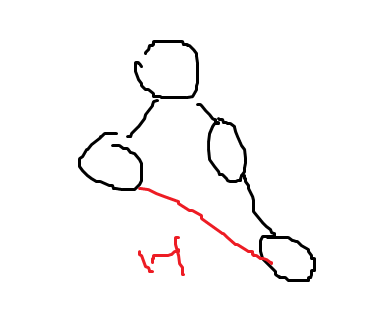
6. G’'’를 알고리즘에 재귀적으로 넣어 나온 MST를 C’라고 하고, C와 C’를 합집합하면 답이다. (왜?)

검은색은 이미 MST에 들어간 애들. 16인 Edge가 Heavy가 안될 확률은 아주 낮다. 다른 Edge가 모두 빠져야 Heavy가 안된다. 하나라도 들어가면 16이 Heavy Edge이다.

만약 위의 빨간색 엣지만 보고이게 Heavy인지 아닌지 어떻게 판단하는가? LCA(공통 조상) 사용하여 제일 큰 Edge를 찾으면 됨. 우리가 배운 LCA 쓰면 Log n.인데 제일 빠른 LCA를 쓰면 상수 시간에 된다? LCA 과정에서 각 노드마다 노드 번호를 적어둘 수도 있지만 가장 큰 Edge Weight를 적어둘 수도 있다. 이를 보고 판단하면 됨.

전체 시간 \(T(n,m)\)은 \(\leq T\left( \frac{n}{8}, \frac{m}{2}\right) + T\left( \frac{n}{8}, \frac{n}{4} \right)+c(n+m)\)이다. 왜 엣지가 \(\frac{n}{4}\)인가? 헤비 엣지를 제거하면 얼마 안남는다?

master thorem에 의해 다 더하면 \(T\left( \frac{n}{8}, \frac{m}{2}\right) + T\left( \frac{n}{8}, \frac{n}{4} \right) = T\left( \frac{n}{2}, \frac{m}{2} \right)\)이다. 따라서 \(T(n,m) \simeq T\left( \frac{n}{2}, \frac{m}{2} \right)\)이고 이는 \(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\dots=2\)와 같으므로 2n, 2m으로 만들어진다. 따라서 \(T(n,m)=O(n+m)\) 처음에 세번 라운드 한 이유가 여기에 있음. 딱 n/8로 만들어야 딱 n/2,m/2로 떨어지므로 기분이 좋음.

몇개가 Heavy냐인건 대충 봤다.

---