알고리즘 6. Backtracking

건국대학교 알고리즘 김성열 교수님의 수업을 정리한 내용입니다.

Backtracking

모든 케이스를 다 따져보다가, 이건 굳이 안따져도 되는 케이스다 싶은 것을 굳이 체크하지 않고 걸러내면 Backtracking이라고 한다. 어떤 조건을 달았을 때 시간복잡도가 어떻게 달라지는지 계산하기는 매우 어렵다.

[!example]- 최대 가치 막대 구하기{title} 길이 i인 막대기의 가치 V[i]가 입력으로 주어졌을 때, 길이 N인 막대기를 잘 나누어서 최대 가치로 나누는 법

예를들어, 길이가 2일 때 가치가 4고, 4일 때 가치가 1이면 4를 2, 2로 쪼개는 것이 최대 가치로 나눈 결과이다.

알고리즘이란 문제의 모든 경우를 일반적으로 해결하는 방법이다. 따라서 다 해보면 된다. 길이 N개인 막대가 주어지면, (0, N), (1, N-1), (2, N-2), …, (N-1, 1), (N, 0)이다. 그렇게 쪼갰을 때, 쪼갠 막대를 또 재귀적으로 부분 막대의 최대 길이를 구하여 그중 가장 가치가 높은 케이스를 선택하면 된다.

막대 N에서 N-4 막대의 최대 가치를 계산하나, 막대 N-2에서 N-4 막대의 최대 가치를 계산하나 결과가 똑같다. 따라서 중복되는 연산이 많으므로 DP를 적용하여 연산을 최적화할 수 있겠다.

DP[i] = 길이가 i인 막대기의 최대 가치 DP[1] = max(DP[0]+V[1]) DP[2] = max(DP[0]+V[2], DP[1]+V[1]) DP[3] = max(DP[0]+V[3], DP[1]+V[2], DP[2]+V[1]) … DP[i] = max(DP[i-j]+V[j]) (0<=j<=i)

[!example]- 정수 쪼개기{title} 0부터 N까지 정수 K개를 더해서 그 합이 N이 되는 경우의 수를 구하는 방법. 숫자를 중복해서 사용이 가능하다.

알고리즘이란 문제의 모든 경우를 일반적으로 해결하는 방법이다. 따라서 다 해보면 된다. 예를들어, 0부터 5까지 정수 3개를 더해서 그 합이 5가 만들게 하고싶다면

1. 0부터 5까지 정수 2개를 더해서 그 합이 4가 되게 하는 경우의 수를 찾고, 1을 더한다.
2. 0부터 5까지 정수 2개를 더해서 그 합이 3이 되게 하는 경우의 수를 찾고, 2를 더한다.
3. …

DP[5][3] = DP[4][2] + DP[3][2] + ... + DP[0][2] DP[i][j] = DP[i-k][j-1], (1<=k<=i)

이때 DP[i][j]는 0부터 i까지 정수 j개를 더해서 그 합이 i가 되게 하는 경우의 수를 기록한 Table이다.

[!example]- N-Queen{title} N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다. 퀸을 놓는 방법의 수를 구하시오.

알고리즘이란 문제의 모든 경우를 일반적으로 해결하는 방법이다. 따라서 다 해보면 된다. 예를들어서, 5 x 5 체스판 위에 퀸 5개를 둔다고 가정하자. 첫번째 행에 첫번째 칸에 두었다면, 다음 기물은 1행, 1열, 그리고 (1, 1)을 포함하는 대각선에는 둘 수 없다. 그것을 기록한다. 그 다음 두번째 행에 세번째 칸에 두었다면, 다음 기물은 2행, 3열, 그리고 (2, 3)을 포함하는 대각선에는 둘 수 없다. 그것을 기록한다. 그 다음 칸이 둘 수 있는 칸이면 두고, 둘 수 없는 칸이면 Skip한다. 이것을 반복하여 5개의 체스 기물을 모두 뒀다면 경우의 수를 1 증가시킨다. 이것은 재귀 + Backtracing을 사용한 알고리즘이다.

State Space

모든 가능한 상태를 나타내는 공간이다. 만약 큐브의 모든 가능한 상태를 그래프로 표현했다고 가정하자. 그럴 때 큐브를 푸는 알고리즘은, 현재 큐브의 상태를 통해 상태 공간 위의 노드를 찾고, 목표 상태까지의 Shorest Path를 찾으면 큐브를 풀 수 있게 된다.

하지만 모든 가능한 상태를 전부 생성하는 것은 불가능하다. 큐브의 모든 가능한 상태는 43,252,003,274,489,856,000이다.. 따라서 State Space를 동적으로 생성하되, 필요 없을 것 같은 부분은 가지치기 하거나, State Space를 너무 깊게 들어왔다 싶으면 Heuristic Function을 사용해서 적당한 가중치를 반환하는 기법을 사용한다.

상태 공간은 그래프로 표현될 수도 있고, 트리로 표현될 수도 있다. 오목, 바둑과 같은 게임의 경우 흑돌 백돌 순서가 서로 번갈아가므로 Tree로 만드는 것이 직관적이고, 큐브의 가능한 상태를 표현하는 경우 큐브의 Action을 Edge로 갖는 Graph로 만드는 것이 직관적이다.

[!example]- 15 Puzzle{title} 퍼즐의 상태를 하나의 노드로 하고, Action을 Edge로 갖는 그래프를 생각하자. 가능한 노드의 개수는 총 16! 가지다.

이 퍼즐의 모든 상태를 Graph로 표현하게 되면, 2개의 Connected Component가 나온다. 각각 ‘정답이 될 수 있는 상태’끼리 연결된 Componet와 ‘정답이 될 수 없는 상태’끼리 연결된 Component이다. 2개로 나뉘어지는 것은 증명되었고, 어렵기 때문에 생략한다.

현재 퍼즐이 State Space 상의 어느 Component에 있는지는 \(\displaystyle\left( \sum_{i} P_{i} + \text{Distance} \right) ~\%~ 2\)라는 규칙으로 판별할 수 있다. 위 값이 0이면 풀 수 있는 퍼즐이고, 1이면 풀 수 없는 퍼즐이다. \(P\)는 Parity의 약어이며, 각 숫자 왼쪽에 자신보다 작은 숫자가 몇 개 있는지를 센 값이다. 예를들어, 15 퍼즐을 하나의 배열로 Flattening하면 \([2, 15, 5, 4, 8, 11, 3, \dots]\) 와 같다.. 2의 Parity는 0이고, 15의 Parity는 1이고, 5의 Parity는 1이고, 이런식으로 각각의 숫자는 각각의 Parity \(P_{i}\)를 갖는다. \(\text{Distance}\)는 빈칸이 현재 위치에서 오른쪽 아래 모서리까지 가기 위해 필요한 Action 횟수이다. 즉 빈칸이 \((2,2)\)에 있으면 \(\text{Distance} = 2\)다.

빈칸을 16이라고 하자. 빈칸과 상하좌우를 교환하면, \(\displaystyle \sum_{i}P_{i}\)와 \(\text{Distance}\) 값이 동시에 바뀐다. 최종적으로는 \(\displaystyle\left( \sum_{i} P_{i} + \text{Distance} \right) ~\%~ 2\) 값이 바뀌지 않아 Component 사이의 이동이 발생하지 않는다.

만약 숫자 두 자리를 임의로 바꾸면, \(\displaystyle \sum_{i}P_{i}\) 만 바뀌고, 최종적으로 \(\displaystyle\left( \sum_{i} P_{i} + \text{Distance} \right) ~\%~ 2\) 의 값이 바뀌어 Component 사이의 이동이 발생한다.

이러한 이유로, 15 Puzzle에서 두 블럭을 바꿔버리면 풀 수 없는 퍼즐이 되거나, 풀 수 없는 퍼즐에서 풀 수 있는 퍼즐이 되기도 한다.

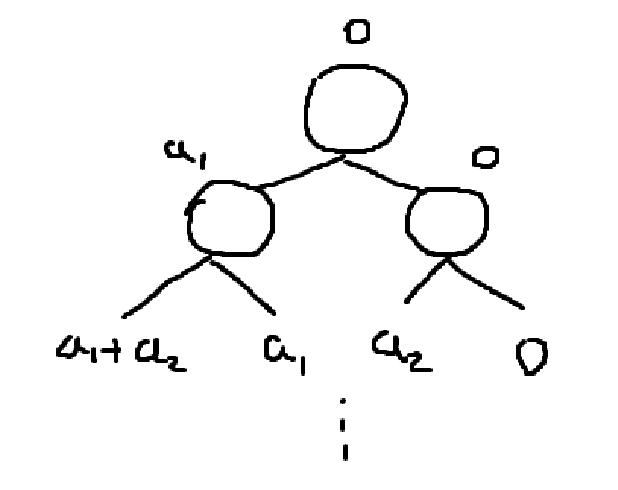
[!example]- Subset Sum Problem{title} 양의 정수 집합 \([a_{1}, a_{2}, \dots, a_{n}]\)이 주어지고, Target Value \(S\)가 주어질 때 합이 \(S\)가 되는 모든 부분집합을 구하는 방법. NP-Complete 문제이다.

양의 정수 집합에서 원소를 선택하는 것을 State라고 생각하여 State Space Tree를 그릴 수 있다. 아무 정수를 선택하지 않은 상태를 Root Node로 잡으면, 그 아래 상태는 \(a_{1}\)를 선택한 상태, 선택하지 않은 상태로 나뉜다. 또 그 아래는 \(a_{2}\)를 선택한 상태, 선택하지 않은 상태로 나뉘고 이를 반복하면 총 트리 노드의 개수는 \(2^n\)개이다. 경우가 너무 많으므로, 의미없는 경우는 Cutoff를 해야한다.

현재까지 경로를 타고 왔을 때 원소의 합을 \(C\)라고 하자. \(C>S\)이거나, \(\displaystyle C + \sum_{j=i+1}^{n}a_{j} < S\)이면 그 Path는 더이상 보지 않아도 된다. \(\displaystyle C+\sum_{j=i+1}^{n}a_{j}<S\)는 앞으로 남은 원소들을 다 더해도 S를 만들지 못하는 경우를 의미한다.

[!example]- Traveling Salesman Problem{title} Weight Graph와 시작 노드 s가 주어진다. s에서 시작하여 모든 노드를 한번씩 방문하고 다시 s로 돌아올 때, Weight가 최소가 되는 경로를 구하라.

NP-Complete 문제다. State Tree를 그려보면, s를 Root Node로 하여 갈 수 있는 상태를 모두 노드로 만들면 된다. 굳이 탐색하지 않아도 되는 경우를 Cutoff해보자.

1. Search Tree를 Depth 우선 탐색할 때 가능한 작전이다. 현재까지 탐색한 완성 경로의 최소 가중치를 알고있다고 하고, 그 값을 \(W\)라고 하자. 또, 현재까지 탐색하면서 거쳐온 경로 가중치의 합을 \(C\)라고 하자. \(C\geq W\)일 때 더이상 탐색하는 것은 의미가 없다.
2. Edge Weight가 모두 양의 정수로 주어졌을 때 가능한 작전이다. 앞으로 방문해야 할 노드의 개수를 \(N\)이라고 할 때 \(C+N\geq W\)인 경우 더이상 탐색은 의미가 없다. 1번보다 더 빨리 끊을 수 있게 되었다.
3. Edge를 전체적으로 한번 정렬하여 그 값을 \([e_{1}, e_{2}, \dots, e_{m}]\)이라고 하자.
   • \(\displaystyle C+\sum_{j=i+1}^{2N}e_{j} \geq W\) 인 경우 더이상 탐색은 의미가 없다.
   • \(\displaystyle \sum_{j=i+1}^{2N}e_{j}\) 의 의미는 무엇인가? 앞으로 노드를 N번 방문해야 하고, 따라서 엣지는 반드시 2N번을 지나야 한다.
   • 그 2N개의 Edge Weight를 더했을 때 나올 수 있는 최솟값을 뜻한다. 이 방법을 사용하여 2번보다 더 빨리 끊을 수 있게 되었다.
4. 3번에서는 전체 그래프에서 정렬된 Edge Set을 사용했지만, 실질적으로 거쳐가는 Edge는 정해져있다. 앞으로 거쳐가야 할 노드를 \([v_{1}, v_{2}, \dots, v_{N}]\)라고 하고, 현재 노드를 \(X\)라고 하자. \(X\) 노드에서 출발하여 \(v_{i}\) 노드를 모두 거치고 \(s\) 노드로 들어가야 한다. \(v_{i}\) 노드들과 인접해있는 Edge중 최솟값의 Edge를 각각 \(x_{i}, y_{i}\)라고 하면 \(\displaystyle C +\left( \frac{1}{2}\sum_{i=j+1}^{N}(x_{j} + y_{j}) \right) \geq W\)인 경우 더이상 탐색은 의미가 없다. \(x_{i}+y_{i}\)를 다 더한것에 2로 나눈 이유는, \(v_{i-1}\) 노드에서 나오는 엣지와 \(v_{i}\)에서 들어가는 엣지가 중복으로 세졌기 때문이다. 이 방법을 사용하면 3번보다 더 빨리 Cutoff할 수 있고, 계산의 오버헤드가 3번보다는 크지만 그래프가 거대해질 수록 이 방법이 더 효율적이다.

[!example]- A Star Algorithm{title} State Space Tree를 깊이 우선, 너비 우선으로 탐색하지 않고 한 Level씩 내려가면서 어느 노드의 Child를 ‘펼칠 지’의 대한 관점으로 접근해도 된다. 그 판단은 Estimation(, Guess, Heuristic)하게 하며, 그런 알고리즘을 통틀어서 \(A^*\) Algorithm라고 부른다. 요즘은 이 Estimation 과정을 AI에게 맡기는 시도가 많다.