알고리즘 5. Graph Algorithm

게시 2024/12/28 업데이트 2025/01/13

By 신희곤

47 분읽는 시간

건국대학교 알고리즘 김성열 교수님의 수업을 정리한 내용입니다.

Graph

문제 상황을 노드와 간선 관계로 표현할 수 있다면, 문제 상황을 그래프로 옮겨서 풀 수 있다. 예를들어 컴퓨터 네트워크를 컴퓨터를 노드, 연결 상태를 간선으로 생각할 수 있다. 또는 미로의 각 칸을 노드, 갈 수 있는 길을 간선으로 표현할 수 있다.

그래프에서 사용 가능한 도구들을 많이 쌓아두면, 문제 상황을 그래프로 옮길 수만 있다면 쉽게 문제를 해결할 수 있다.

Traversal

그래프의 각 노드를 한번씩 순회하는 것을 Traversel이라고 한다. 알고리즘은 다음과 같다.

아무 노드에서 시작해서 O(1)
시작 노드를 자료구조에 넣는다. O(1)
자료구조가 빌때까지 반복한다. O(n)
    자료구조에서 노드를 꺼내서 (자료구조에 따라 다르다. O(1), O(logn), ...)
    어떤 계산을 처리하고 (상황에 따라 다르다.)
    Visit 처리 후 O(1)
    인접한 노드를 자료구조에 넣는다. (한 노드에서 많이 추가되면 다른 노드에서는 시간을 덜 쓰게 된다. 총 +O(m))

Traversal의 최소 시간 복잡도는 \(O(n+m)\)이다. 어떤 자료구조를 사용하냐에 따라서 다른 알고리즘을 만들어낼 수 있다.

자료구조가 Stack이면 DFS
Queue면 BFS
Priority Queue일 때 Edge Weight가 우선순위면 Prim Algorithm, Distance from s가 우선순위면 Dijkstra, 아무 함수나 넣을 수 있으면 \(A^*\) Algorithm와 같다.

[!example]- 두 노드 사이의 Path가 존재하는가?{title} 둘 중 한 노드에서 Traversel을 시작했을 때 다른 노드를 방문하면 두 노드 사이의 Path가 존재함을 알 수 있다. Traversel을 사용하므로 \(O(n+m)\)만에 해결한다.
정말 두 노드 사이의 Path가 있을 때 Traversel하면 반드시 방문하게 될까? 귀류법으로 증명 가능하다. 먼저 두 노드 사이의 길이 있는 경우를 살펴보자. 시작 노드를 \(s\), 목표 노드를 \(t\)라고 하자. \(s\) 노드에서 Traversel를 시작했을 때 \(t\) 노드를 Visit하지 않는다고 가정하자. Visit하지 않으려면 \(s\) 노드와 \(t\) 노드로 가는 길 중간에 Visit가 안된 노드가 존재해야 한다. 하지만 Path가 있으면 노드끼리 연결되고, 노드끼리 연결되면 Traversal은 반드시 방문하게 된다. 따라서 모순이다.
위 사실을 이용하면 \(s\)와 Mark가 된 두 노드 사이에는 길이 존재한다는 Invariant를 만들 수 있다. Mark가 된 노드와 인접한 노드를 Mark하면 \(s\)와 Path로 연결되는 노드가 점점 확장된다. Traversal 종료 이후 인접한 모든 노드들은 \(s\)와 Path가 존재한다. 만약 Mark가 되지 않았다면 \(s\)와 Path가 존재하지 않는다는 것과 같다.

[!example]- Find Connected Component{title} Connected Component는 노드끼리 서로 연결되었을 때 만들 수 있는 최대 크기의 노드 집합이다. 이것을 찾는 방법은 그냥 Traversal을 해보면 된다. 아무 노드에서 Traversal을 시작한다. 이후 Visit Array를 보고 방문이 안된 노드를 시작 노드로 삼아 다시 Traversal하는 것을 반복하면 Graph 내의 Connected Component를 찾을 수 있다.

[!example]- 두 노드 사이의 여러 Path 중 Edge Weight의 Maximum이 가장 작은 Path를 찾아라.{title} 목표는 \(O((n+m)\log m)\)에 해결하는 것이다. 아이디어는 \(\log m\)이 있으므로 Edge를 정렬하고 Binary Search를 사용하는 것이다. Edge 정렬은 \(O(m\log m)\) 시간이 걸리므로 \(O((n+m)\log m)\) 시간을 해치지 않는다.
정렬한 Edge를 \([e_{1}, e_{2}, \dots, e_{m}]\)이라고 하자. 이 정렬한 List의 중앙 Index를 \(M\)이라고 하자. 이라고 하자. 시작 노드를 \(s\), 도착 노드를 \(t\)라고 하자. \(s\)에서 시작하여 Traversal을 돌린다. Traversal 과정에서 \(Weight > M\)이면 그 경로는 버린다. 이렇게 했을 때 \(t\) 노드가 방문되면 가능한 최소 Weight는 \([e_{1}, e_{2}, \dots, e_{M}]\) 와 같다. \(t\) 노드가 방문되지 않으면 가능한 최소 Weight는 \([e_{M+1}, \dots, e_{m}]\) 안에 존재한다. 이를 반복하여 하나의 \(e\)를 특정하면 그 \(e\)의 weight가 \(s\to t\)로 가는 Path 중 Edge Maximum의 최솟값이 된다.
Traversal에 \(O(n+m)\) 시간이 걸리고, 이를 \(\log m\)번 수행하므로 총 시간은 \(O((n+m)\log m)\)이 사용된다.

Pre Number, Post Number

Traversal을 재귀적으로 구현하면 다음과 같다.

RDFS(Node s)
{
    s가 Visit(Mark) 되어있으면 return.
    s를 Visit
    여기서 작업하면 BFS (Preorder)
    RDFS(모든 인접한 노드)
    여기서 작업하면 DFS (Postorder)
}

이때 Preorder 부분에서 방문한 노드의 번호를 붙이면 Pre number, Postorder 부분에서 방문한 노드의 번호를 붙이면 Post number라고 한다. 즉 Pre number는 들어가면서 붙이는 번호, Post number는 나오면서 붙이는 번호다. 이는 그래프의 속성 Number로 유용하게 사용될 수 있다.

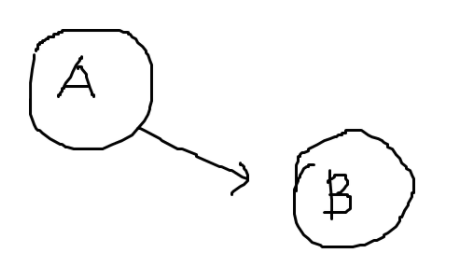
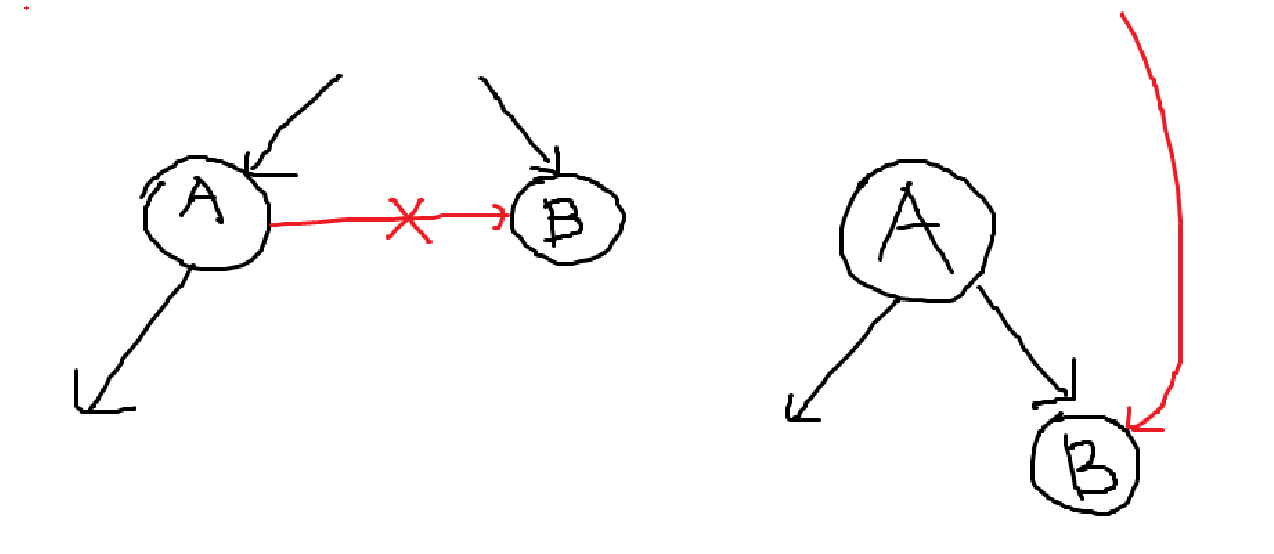
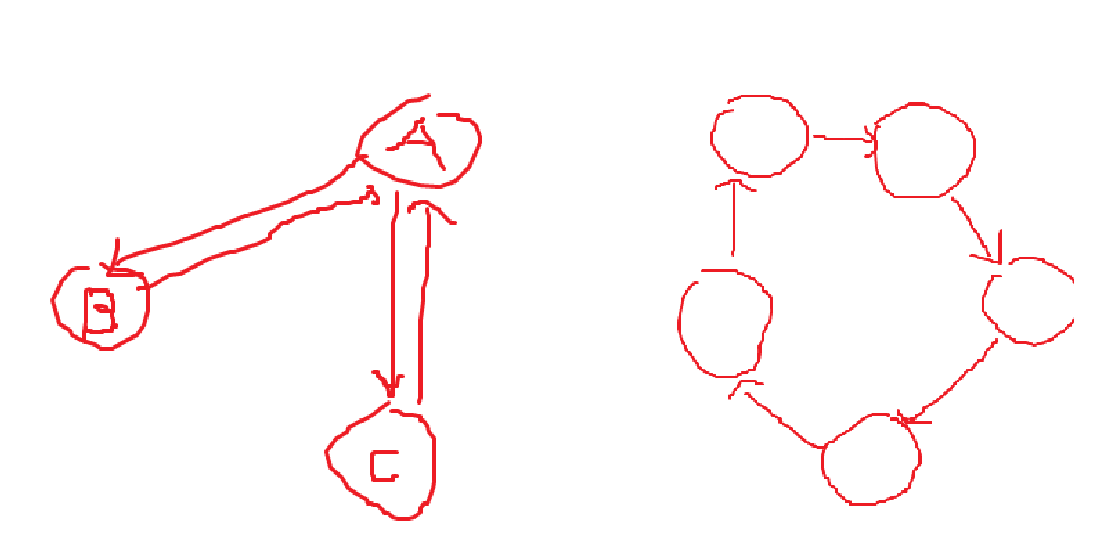
Pre number는 탐색 순서를 의미한다. DFS가 어디서 시작하냐에 따라 달라진다. 예를들어 위와 같이 노드가 A, B가 있는 Directed Graph가 존재한다. A 노드에서 DFS를 시작하면, Pre number는 A에 1, B에 2가 붙는다. B 노드에서 DFS를 시작하면, B에 1이 붙고, 다음 DFS를 다시 시작할 때 A에서 시작하여 2가 붙는다.

Post number는 DFS가 어디서 시작해도 유지되는 속성이 있다. 바로 Max, Min post number이다. 만약 그래프가 DAG라면 Max post number는 항상 Indegree가 0인 노드 중에 존재하고, Min post number는 항상 Outdegree가 0인 노드에 존재한다. 위 그래프를 예시로 들어보자. DFS가 A 노드에서 시작하면, B로 진입하여 Post number를 B=1을 붙이고 나와서 A=2가 붙는다. 반대로 DFS를 B에서 시작하면, B에서 갈 곳이 없으므로 B=1을 붙인다. 이후 A에서 DFS를 시작하여 A=2가 붙는다.

만약 Indegree가 0인 노드가 없다면, DAG가 아니고 Cycle이 존재한다는 뜻이다. 그래프를 SCC 기반의 Supergraph로 생각하면 Supergraph는 DAG이고, Supergraph의 Indegree가 0인 노드 안에 Max post number가 존재하고, Outdegree가 0인 노드 중에 Min post number가 존재한다. 증명도 가능하다.

Indegree가 0인 Supergraph 상의 노드를 A 노드라고 하자. A 노드 안에서 DFS를 시작하는 경우를 보자. 만약 Outdegree가 존재하면, 반드시 다른 노드로 이동하고, 그 다른 노드에서 Post Number를 붙이고 다시 A 노드로 돌이온다. 그래프가 DAG이므로, 전체를 순환하고 최종적으로 A 노드에 다시 돌아오게 된다. 따라서 마지막 Post Number는 A 노드 내에서 붙게 되며, Max post number는 A 노드 안에 존재함을 알 수 있다.

A 노드가 아닌 곳에서 DFS를 시작하는 경우를 보자. 시작 노드에서는 A 노드로 갈 수 없다. 따라서 시작 노드와 연결된 다른 노드에 Post number를 붙이고 다음 DFS를 진행해야 한다. 따라서, 다른 노드에서 시작하는 경우 그 노드와 연결된 모든 노드의 Post number는 A 노드 내의 Post number보다 작다. 따라서, A 노드의 Post number는 다른 시작 노드의 Post number보다 크다는 것을 알게 된다.

Event Queue

\(n \times m\) 배열이 입력으로 주어지고, 그 배열은 몇몇개의 감염된 칸이 존재한다. 어떤 칸의 상하 좌우 중 2개 이상 감염되었다면 추가로 감염된다. 감염이 전부 끝나면, 어떤 칸이 감염되어 있을까?

입력이 \(nm\)이므로 \(O(nm)\) 안에 해결하면 가장 빠르다. 만약 배열 전체를 한번 보고 감염시키고, 다시 한번 보고 감염시키고를 반복하면 \(O((nm)^2)\) 시간이 걸린다. 이를 해결하기 위해 Event Queue를 도입하자.

Event Queue는 말 그대로 Event를 Queue에 넣는 것이다. 최초에 배열 전체를 한번 보고 감염되야 할 칸이 감염되었다는 Event를 Queue에 넣는다. 이후 Queue에서 하나씩 꺼내서 칸을 감염시킨다. 그 칸이 감염됨으로써 추가적으로 감염될 가능성이 있는 칸은, 내가 방금 꺼낸 칸의 인접한 칸 뿐이다. 따라서 인접한 칸이 감염될지의 여부를 체크하면 \(O(4)\)밖에 안걸린다. 체크하고 감염되는 칸이 있다면 Event Queue에 넣는다. 이를 Queue가 빌 때까지 반복한다. 최초에 시간 \(O(nm)\)을 사용하고 Queue의 Push Pop은 \(O(1)\), 감염 여부 체크도 \(O(1)\)만에 가능하다. 따라서 문제를 \(O(nm)\) 시간에 해결한다.

DFS Tree on Undirected Graph

Tree를 하나 만들고, DFS 과정에서 방문하는 순서대로 Tree에 추가하면 그 Tree를 DFS Tree 라고 부른다. 보통 트리를 분석하는 것이 그래프를 분석하는 것보다 쉽다. 따라서 복잡한 그래프에서 DFS를 돌려 Tree를 만들어낸 뒤, 그 Tree를 분석해보자라는 것이 아이디어이다. 몇몇 문제에 효과적이며, 모든 문제가 DFS Tree로 풀리지는 않는다.

DFS Tree를 그림으로 그리는 방법은 다음과 같다.

전진한 방향을 화살표로 표시한다.
항상 먼저 방문한 곳을 왼쪽에 그리자고 약속한다.

DFS Tree는 어느 노드를 시작 노드로 잡냐, 구현에서 어느 노드를 먼저 방문하냐에 따라서 여러가지 모양의 DFS Tree가 생성될 수 있다.

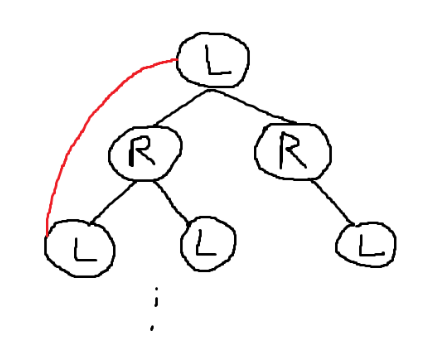
Undirected Graph에서 만들어내는 DFS Tree의 가장 큰 특징은, Back edge는 존재하고 Cross edge는 존재하지 않는다는 성질이다.

DFS Tree에서 그려진 Edge는 그래프 위의 모든 Edge를 표현하지 않는다. 그려지지 않은 Edge를 DFS Tree에서 그려보면 아래에서 위로 올라가는 Edge는 존재한다. 이를 Back edge라고 한다. 하지만 좌우로 연결된 Edge는 존재하지 않는다. 이를 Cross edge라고 한다.

왜 Cross edge가 존재하지 않을까? 왼쪽과 오른쪽이 연결된 Cross edge가 존재할 수 있다고 가정해보자. 왼쪽 노드를 \(L\), 오른쪽 노드를 \(R\)이라고 하자. \(L\)과 \(R\)의 Cross edge가 존재한다는 뜻은 \(L\)과 \(R\)이 인접 노드 관계라는 뜻이다. DFS Tree는 항상 먼저 방문한 노드가 왼쪽에 그려지므로, \(R\) 노드는 Tree에 그려지지 않은 상태다. 따라서 \(R\) 노드는 \(L\) 노드의 자식으로 그려져야 한다. 이는 가정과 모순이므로, Cross edge는 존재할 수 없다.

DFS Tree on Directed Graph

Directed Graph에서 DFS Tree를 뽑아내면, 다음과 같은 성질이 존재한다.

어디서 DFS를 시작하냐에 따라 1개의 DFS Tree가 나올 수도, 여러개의 DFS Tree가 나올 수 있다.
Back Edge가 존재한다.
Forward Edge가 존재한다.
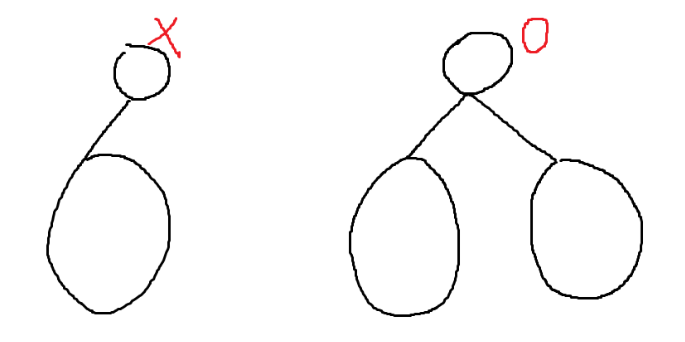
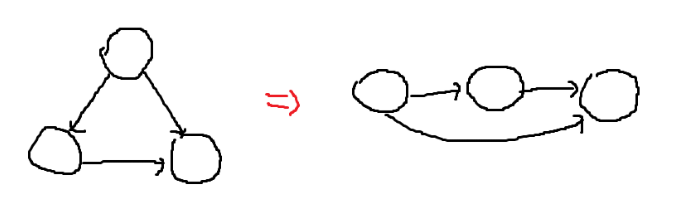
Left Cross Edge가 존재한다.
Right Cross Edge가 존재할 수 없다.
하나의 SCC는 반드시 단일 Tree 내에 존재한다.

왜 Left Cross Edge는 존재할 수 있는데 Right Cross Edge는 존재할 수 없는가? DFS Tree 특성상 먼저 방문한 곳이 왼쪽에 그려진다. 만약 왼쪽 그림과 같은 Right Cross Edge가 존재한다면, 애초에 Right Cross Edge로 연결된 노드가 자식으로 그려져야 하므로, DFS Tree와 모순이다. 따라서 Right Cross Edge는 존재할 수 없다. 위 그림을 이해하면, Forward Edge가 존재할 수도 있다는 것을 알 수 있다. Left Cross Edge 또한 충분히 존재하는 Example을 생각해볼 수 있다.

Bipartite Graph

노드를 두 그룹으로 나눈다. 두 그룹 사이의 Cross edge만 존재하고 그룹 내의 노드끼리 연결된 edge가 하나도 없는 경우를 ‘적어도 하나’ 만들 수 있다면 그 Graph를 Bipartite Graph라고 정의한다. DFS Tree를 사용하면 바로 Bipartite Graph인지 아닌지 판단할 수 있다.

노드를 두 그룹으로 분리해야 하는데, Root 노드와 연결된 노드는 반드시 Root 노드와 다른 그룹에 배치해야 한다. Root 노드를 임의로 왼쪽에 놓으면, 그 자식 노드들은 전부 오른쪽에 배치되어야 한다. 이를 반복하면 두 그룹으로 나눌 수 있다. 만약 그림과 같은 Back edge가 존재한다면, 이 그래프는 절대로 Bipartite Graph로 만들 수 없다. Bipartitle Graph가 되는 경우는 Root 노드가 왼쪽에 오는 경우 오른쪽에 오는 경우밖에 없는데, 위와 같은 Back edge가 존재한다면 두 경우 모드 그룹 내의 노드끼리 연결된 edge가 존재하기 때문이다.

Cut Vertex

Cut Vertex란, 없앴을 때 그래프가 두개로 분리되는 정점을 의미한다. 엄밀한 정의는 다음과 같다. 두 임의의 노드 \(x\), \(y\)를 잇는 모든 Path가 존재하고, 모든 Path가 어떤 노드 \(s\)를 지나간다면 그 \(s\)를 Cut Vertex라고 정의한다.

Cut Vertex를 찾는 아이디어는, DFS Tree를 통해 찾는 것이다. 쉽게 알 수 있는 특징은, Tree의 Leaf는 절대 Cut Vertex가 아니다. 왜냐하면 Leaf 노드를 제거해도 Tree는 절대 쪼개지지 않고, Tree가 쪼개지지 않는다는 것은 Graph가 쪼개지지 않는다는 것과 같기 때문이다.

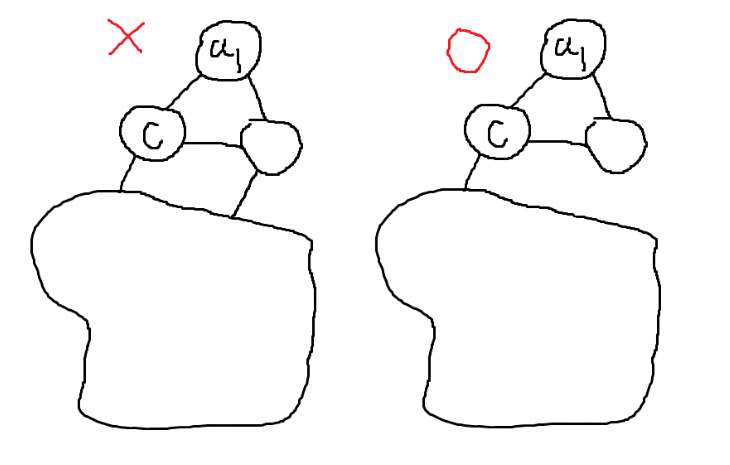
그리고 Root 노드의 Child가 1개면 Cut Vertex가 아니고, 여러개만 Cut Vertex이다. Cut Vertex가 될 조건은 두 임의의 노드 \(x, y\) 사이의 모든 Path가 Cut Vertex를 거쳐야 한다. Root의 Child가 1개인 경우는 두 임의의 노드 \(x, y\) 사이의 모든 Path는 굳이 Root 노드를 거치지 않아도 연결되어 있다. 이 경우 Root는 Cut Vertex가 아니다. Root의 Child가 여러개인 경우는 다르다. 왼쪽 Subtree의 노드 중 하나를 \(x\), 오른쪽 Subtree의 노드 중 하나를 \(y\)라고 하면 \(x\to y\)로 가는 모든 경로는 반드시 Root 노드를 거쳐야 한다. 그 이유는 Cross edge가 존재하지 않기 때문이다. 이 경우 Root 노드는 Cut Vertex이다.

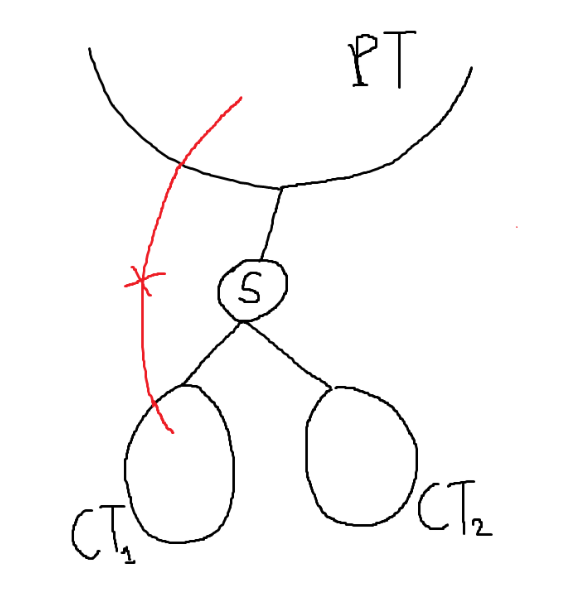
이제 일반적인 Cut Vertex 판정 방법을 생각해보자. Cut Vertex인지 아닌지 판정할 노드를 \(s\)라고 하자. \(s\)가 Root 노드거나 Leaf 노드라면 위의 방법을 사용해서 바로 판단할 수 있다. 둘다 아니면, Child Subtree와 Parent Subtree가 존재하게 된다. \(s\)와 연결된 Child Subtree를 \([CT_{1}, CT_{2}, \dots, CT_{N}]\)이라고 하자. Parent Subtree를 \(PT\)라고 할 때 \(PT\)와 \(CT_{i}\) 사이의 Back edge가 존재하지 않는 경우가 하나라도 존재하면, \(s\)는 Cut Vertex이다.

\(CT_{i}\)가 다른 Subtree와 연결되어 있는 가능성은 \(PT\)와의 Back edge또는 다른 \(CT\)와의 Cross edge 뿐이다. Cross edge는 존재하지 않으므로, \(PT\)와의 Back edge 여부만 체크하면 된다. \(PT\)와의 Back edge가 존재하지 않는 경우 \(s\)를 제거하면 \(PT\)와 \(CT_{i}\)가 서로 분리된다.

\(CT_{i}\)와 \(PT\) 사이의 Back Edge가 존재하는지 알아내는 방법이 있어야 한다. 구현을 위해 각 노드에 Pre number를 붙인다. Pre number는 정확히 DFS Tree의 방문 순서대로 붙는다. 위에서 내려가는 한 경로 위에서는 Pre number가 작을 수록 Tree 에서 위에 있게 된다.

각 노드마다 ‘Back Edge를 통해 갈 수 있는 가장 최소 Pre number(=가장 높은 노드)‘을 기록한다. 이 값을 \(Low(u)\)로 정의하자. \(CT_{i}\)의 Root Node를 \(u\)라고 할 때, \(Low(u) \geq Pre(s)\)를 만족하면 \(s\)는 Cut Vertex이다. \(Low(u)\)가 높을 수록 Tree상에 아래에 있기 때문에, 위 조건이 만족되면 Back edge를 통해 갈 수 있는 노드가 \(s\) 이하와 같다. 따라서 \(PT\)의 Node와 연결된 Back edge가 없다.

DFS 과정에서 Pre number를 붙이고, \(Low[i]\)를 정의 후 Pre number가 큰 순서대로, 즉 아래에 있는 노드부터 \(Low[i]\) 값을 계산하면 된다. 점화식은 아래와 같다.

\(\displaystyle Low[i] = \text{min} \left(Pre(i), \underset{u \in \text{Child}(s)}{\text{min}} Low(u), \underset{t \in \text{Adjacent}(s)}{\text{min}} Pre(t)\right)\)
\(\text{Child(s)}=\) 노드 \(s\)의 모든 Child 노드 집합.
\(\text{Adjacent}(s) =\) 노드 \(s\)와 인접한 모든 노드 집합.

위 점화식은 \(Pre(i)\), 모든 자식 노드 중 가장 작은 \(Low\)값, \(i\) 노드와 인접한 노드 중 가장 작은 Pre number 셋 중 가장 작은 값을 계산하는 식이다. Postorder에서 \(Low[i]\)를 계산하면 자동으로 아래에서부터 계산하게 된다. 즉 Postorder에서 \(Low[i]\)를 계산 후 Cut Vertex를 판정하면 한번의 DFS만 돌려도 된다.

Traversal 과정에서 \(O(n+m)\)을 소모하고, \(Low[i]\)를 계산하는데 인접한 노드를 봐야 하므로 간선 개수만큼 계산이 일어나므로 \(O(m)\)를 소모한다. 따라서 Cut Vertex를 \(O(n+m)\) 시간 내에 계산 가능하다.

Cut Edge

그냥 모든 엣지 중간에 노드를 하나 끼워 넣고 Cut Vertex를 찾는다. 만약 끼워놓은 노드가 Cut Vertex라면, 그 Edge가 Cut Edge와 같다.

Biconnected Graph (BCC)

BCC는 모든 노드가 2중으로 연결되어 있는 경우 Biconnected Graph이다. 즉 Cut Vertex가 존재하는 경우 Biconnected Graph가 아니다.

Biconnected Component는 Biconnected 조건이 만족되는 최대 Node 집합을 의미한다. 따라서 한 그래프에 여러개의 Biconnected Component가 있을 수 있다. Component는 더이상 늘릴 수 없을 때 까지 늘린 Node Group을 의미한다.

만약 그래프 내에 Cut Vertex가 없다면 Graph 전체가 Biconnected Component이다. 만약 그래프 내에 Cut Vertex가 딱 한개만 있다면, Cut Vertex는 두 Biconnected Compoent를 연결하는 매개 노드와 같고, Cut Vertex를 기준으로 그래프를 두개로 나누면 각각의 Biconnected Component를 찾은 것과 같다. 따라서 모든 Cut Vertex를 찾고, Cut Vertex를 기준으로 그래프를 쪼개면 모든 부분 그래프 내에 Cut Vertex가 존재하지 않으며, 따라서 모든 부분 그래프는 Biconnected Component와 같다.

Cut Vertex를 찾는데 \(O(n+m)\) 시간이 걸리고, 두 그래프를 끊는데도 \(O(n+m)\) 시간이면 충분하다. 따라서 BCC를 찾는데 걸리는 총 시간은 \(O(n+m)\)이다.

Directed Acyclic Graph (DAG)

DAG란, Cycle이 없는 방향 그래프를 뜻한다.

DAG의 Use Case 중 하나는 공장이다. 공장 과정에 Cycle이 있으면 제품이 무한 뺑뺑이돌면서 완성되지 않을 것이므로, 공장의 생산 프로세스는 DAG이다. 만약 제품이 만들어지는 시간을 줄이고 싶다면, 과정을 DAG로 표현 후 Longest Path를 찾아서 그 Path의 길이를 줄여야 한다. 이런 Use Case가 존재한다.

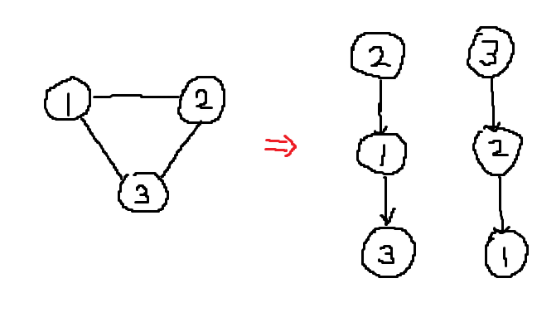
Topological Sort

위 그림과 같이 모든 간선이 오른쪽을 향하도록 DAG의 노드를 정렬하는 것을 Topological Sort라고 한다. 다른 노드에서 들어오는 간선 개수를 Indegree라 하자.

모든 DAG는 항상 Topological Sort 가능하다. 증명은 알고리즘이 항상 DAG를 정렬해주므로, 알고리즘 자체에 의해 증명된다. 보통 Topological Sort를 해놓고 문제를 푸는게 아닌, Sort를 하면서 문제를 푸는 경우가 많다.

Cycle이 없는 그래프에서는 반드시 indegree가 0인 노드가 적어도 하나 존재한다. 만약 Cycle이 없으면서 indegree가 0인 노드가 없는 그래프를 가정하자. 어떤 임의의 노드 하나를 고르면 그 노드의 indegree는 반드시 0이 아니다. 따라서 어딘가에서 들어오는 간선이 존재한다. 간선을 따라 올라가면 그 노드 또한 indegree가 0이 아니다. 이를 무한히 반복해도 하나의 그래프를 만들 수 없다. 따라서 모순이며, Cycle이 없는 그래프에선 반드시 indegree가 0인 노드가 적어도 하나 존재함을 증명한다.

indegree가 0인 노드를 찾아서 그래프에서 제외한다. DAG에서 노드를 뺀다고 없던 Cycle이 생기지 않는다. 따라서 indegree가 0인 노드를 뺀 그래프도 DAG이고, DAG에는 indegree가 0인 노드가 반드시 하나 존재한다. 이를 응용하면, indegree가 0인 노드를 찾아서 그래프에서 제외하고, 순서대로 왼쪽에 두면 항상 Topological Sort가 가능하다.

indegree가 0인 노드를 찾기 위해 모든 Edge를 체크해야 하므로 \(O(m)\) 시간이 걸리고, 이 과정을 \(n\)번 반복하므로 시간이 \(O(nm)\)이 소요된다. 하지만 굳이 indegree가 0인 노드를 매번 처음부터 찾을 필요가 없다. 왜냐하면, 그래프에서 노드를 제외했을 때 indegree가 0이 될 가능성이 있는 노드는 제외한 노드가 가리키는 노드밖에 없기 때문이다. Event Queue를 사용할 수 있다.

최초에 Indegree가 0인 노드를 모두 찾아 Event Queue에 넣는다. 이 과정에서 \(O(m)\)을 사용한다. Queue에서 노드를 하나씩 꺼내서 그래프에서 제외한다. 이후 노드가 가리키던 노드의 Indegree가 0이 된다면 그 노드를 Event Queue에 추가한다. 이것을 Event Queue가 빌때까지 반복하면, 총 \(n\)번 반복한다. Push Pop 연산은 상수시간이므로 총 시간은 \(O(n+m)\)만에 Topological Sort가 가능하다.

[!tip]- 더 빠르고 편하게 Topological Sort를 계산하는 방법{title} DFS를 한번 해서 각 노드에 Post number를 붙인다. 이후 Post number가 Decreasing하는 순서대로 출력하면 자동으로 Topological Sort가 된다. 그 이유는, DAG라면 Max post number는 항상 Indegree가 0인 노드가 갖기 때문이다.
또는 Post number를 붙인 후 모든 Edge의 방향을 뒤집어서 Post number가 작은 순서대로 출력해도 똑같은 결과를 갖는다.

Longest Path

Shorest Path는 Dijkstra를 사용하면 된다. 일반적으로 Longest Path를 찾는 문제는 NP-Complete이다. 하지만 DAG의 경우는 Longest Path를 좀 쉽게 찾을 수 있다.

먼저 DAG를 Topological Sort한다. 이후 가장 왼쪽 노드에서 시작하여 다음 노드로 가는 경로 중 가장 긴 Weight Edge들만 취해서 가면 된다. Topological Sort 한번 하는데 \(O(n+m)\)이고, 엣지들 체크하면서 경로를 따라오면 \(O(m)\)이 걸린다. DAG라는 특수한 경우 Longest Path를 찾는 문제는 NP 문제가 된다.

우주정거장 문제

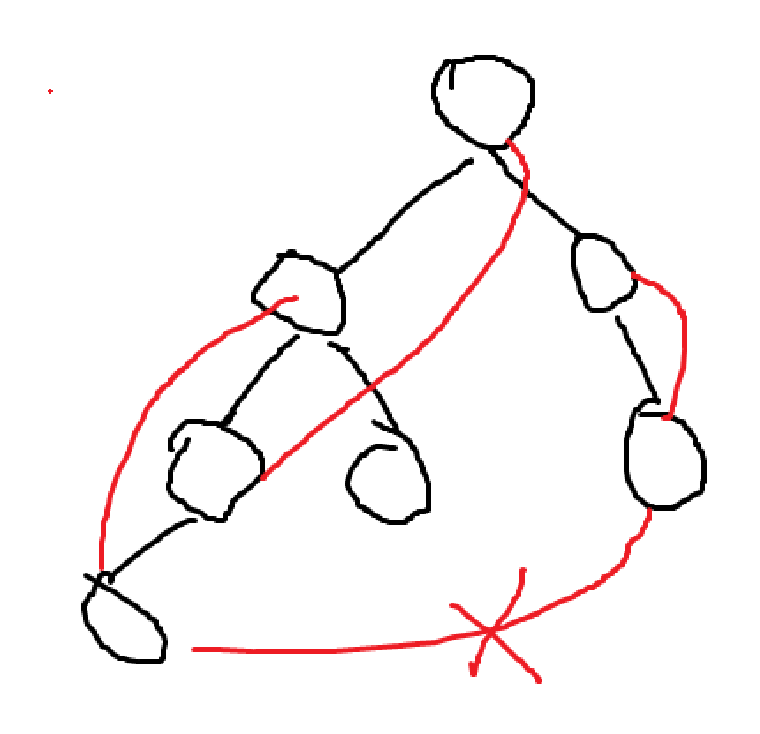
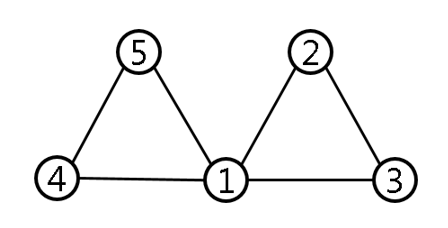
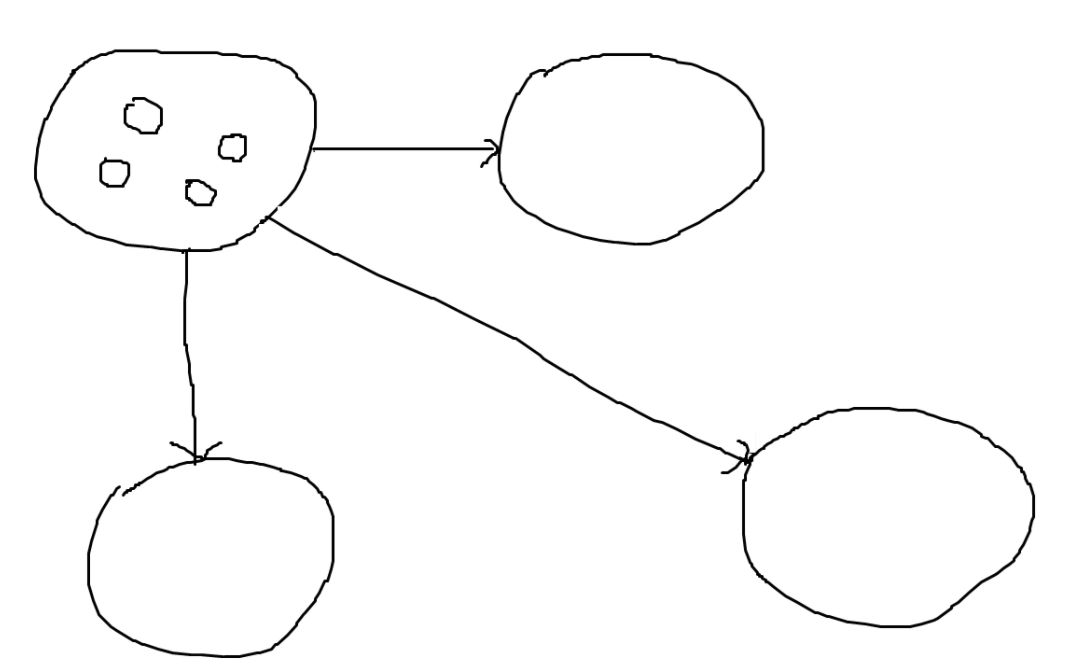
그래프가 주어지고, 그래프 내에서 삼각형을 이루는 정점 중 degree가 2인 정점만 제거 가능하다. ‘잘 제거하여’ 최소 개수의 정점을 구하라. 위의 그림의 경우 1번 노드는 제거할 수 없다.

아이디어는 Topological Sort와 비슷하다. degree가 2인 모든 노드를 찾아 Event Queue에 넣는다. Event Queue에서 정점을 하나씩 꺼내어 그 노드가 삼각형에 속하는지 판단한다. 삼각형에 속하면 노드를 제거하고, 그 노드와 연결되어있던 노드 중 degree가 2로 변하는 노드를 Event Queue에 넣는다. 이 과정을 반복하면 조건에 만족하는 모든 노드를 제거할 수는 있다.

위 알고리즘대로 제거했을 때 항상 ‘최소 개수의 정점’만 남을까? degree가 2인 노드가 여러개 존재할 수 있다. 어떤걸 먼저 빼냐에 따라서 그래프 모양이 바뀔 수 있는데, 어떤 케이스는 정점이 좀 많이 남고, 어떤 케이스는 정점이 덜 남는 상황이 존재할 수 있을까? 이를 검증해야 한다.

노드를 제거하는 순서를 기록한 두개의 \(\text{seq } A = \{ a_{1}, a_{2}, \dots\}\)와 \(\text{seq } B = \{b_{1}, b_{2}, \dots \}\)를 가정하자. 두 시퀀스의 길이가 항상 같은지, 아니면 다른 경우가 있는지 증명해야 한다.

(1) \(a_{1} = b_{1}\)인 경우 문제가 되지 않는다. (2) \(a_{1} = b_{k}\)인 경우, \(b_{k}\)를 sequence의 맨 앞으로 가져와 \(\text{seq } B' = \{ b_{k}, b_{1}, b_{2}, \dots, b_{q} \}\) 시퀀스로 대체할 수 있다. 왜냐하면, \(a_{1}\)이 가장 먼저 지워졌다는 것은 \(a_{1}\)의 degree가 2라는 것이고, \(a_{1}=b_{k}\) 관계가 \(b_{k}\)의 degree가 2임이 보장된다. 따라서 두 시퀀스 모두 똑같은 노드를 먼저 제거하므로, 이후 상황이 완전히 동일하여 문제가 되지 않는다. (3) \(a_{1} \notin \text{seq }B\)인 경우가 문제다. 이는 \(b_{1}, b_{2}, \dots\)를 삭제하다가 \(a_{1}\)과 연결된 어떤 노드가 지워져 \(a_{1}\)을 \(\text{seq } B\)에서 지우지 못했다는 뜻이다. 초기 \(a_{1}\)의 degree는 2이고, \(\text{seq B}\)를 적용 후 \(a_{1}\)의 degree는 1이 된다.

따라서 항상 위 그림과 같은 모양이 될 것이다. \(a_{1}\)과 연결된 유일한 노드를 \(c\)라고 하면, \(c\)는 반드시 Cut Vertex이다.

\(c\)와 연결된 삼각형 내의 두 노드는 둘다 지워질 가능성이 있는 노드이므로, degree가 2이다. \(c\)를 제외한 나머지 두 노드의 degree가 2이므로 왼쪽과 같은 모양은 불가능하고, 오른쪽과 같은 모양만 가능하다. 이런 특수한 경우 Cut Vertex가 불변이다. 일반적으로 Cut Vertex는 불변이 아니다.

입력 그래프에서 Cut Vertex를 찾고, Cut Vertex를 기준으로 그래프를 분리하면 나머지 그래프는 모두 Biconnected Component이다. 개수가 달라질 가능성이 있는 케이스는 (1), (2), (3)중 (3) 뿐이고, (3)의 케이스는 Cut Vertex와 연결된 Leaf Biconnected Component의 노드가 다 사라지고 딱 한개의 노드만 남는 케이스다. Cut Vertex가 이 경우 불변이고, 따라서 총 노드의 수도 변하지 않는다.

따라서 어떤 순서로 제거해도 최종적으로 남는 노드의 개수는 항상 동일하므로, 처음에 제기한 알고리즘을 마음 편히 사용해도 된다.

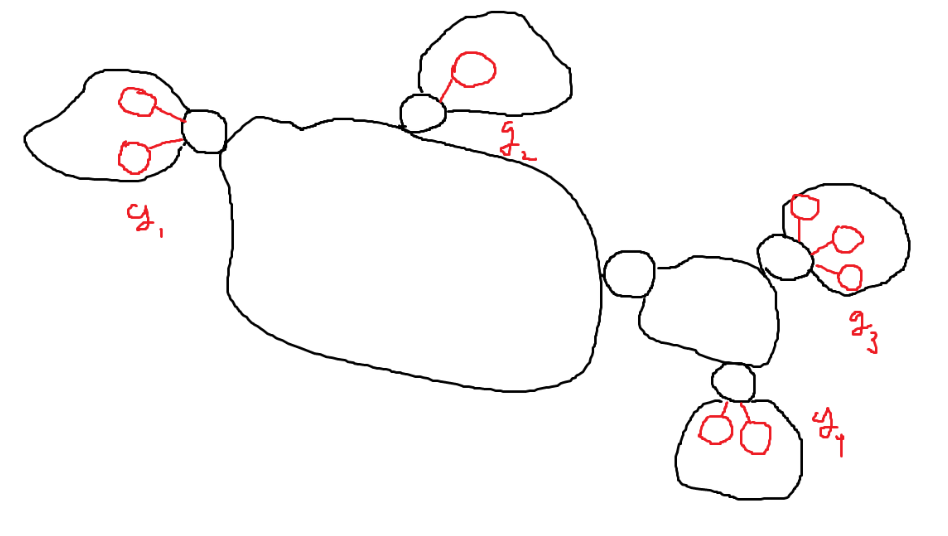
[!tip]- 만약 모든 가능한 그래프의 케이스를 구하라고 한다면?{title}
Leaf BCC의 개수가 \(k\)개일 때 Cut Vertex와 연결된 노드의 개수를 각각 \(g_{1}, g_{2}, \dots, g_{k}\)라고 하자. 그래프의 분기점은 Leaf BCC에서 Cut Vertex와 연결된 노드 중 어떤 노드를 제거하냐에 따라 갈린다. 즉 모든 가능한 그래프의 케이스는 모두 곱한 \(g_{1} g_{2} g_{3} \dots g_{k}\)와 같다.

Strongly Connected Graph

Strongly Connected란 Directed Graph에서 두 노드가 있을 때 한쪽에서 다른 쪽으로 가는 Path가 둘다 존재하는 경우를 뜻한다. 즉, 어떤 Node Group가 있을 때, Group의 한 노드에서 Component에 포함된 다른 모든 노드로 갈 수 있어야 하고, 이 Node Group을 Maximal하게 늘린 것을 Strongly Connected Component, SCC라고 정의한다. 편의상, 1개의 노드만 있는 것도 SCC라고 부르자고 약속한다.

SCC는 어떤 모양으로 생겼을까? 생각해보면, SCC는 반드시 순환 구조, Cycle을 가질 수 밖에 없다. 왜냐하면, SCC 내에서 A에서 다른 노드로 가는 길은 반드시 존재하고, 그 다른 노드로부터 다시 A로 돌아오는 길이 반드시 존재하기 때문이다. 즉 A에서 출발해서 다시 A로 돌아올 수 있는 Cycle 구조가 SCC 안에는 한개 이상 존재한다. 즉 SCC는 Cycle의 일반화된 구조라고 볼 수 있겠다. SCC는 반드시 1개 이상의 Simple Cycle을 가지며, 단일 Simple Cycle이 하나의 SCC가 될 수 있고, 여러개의 Simple Cycle이 하나의 SCC가 되는 구조가 될 수 있다.

Graph 문제를 해결하는 아이디어 중 하나는, 복잡한 그래프에서 DFS Tree를 뽑아내어 Tree의 성질을 이용해서 문제를 해결하는 것이다. 이 경우도 DFS Tree를 이용해볼 수 있다. Directed Graph에서 DFS Tree를 만들면, DFS Tree가 갖는 성질은 다음과 같다.

어디서 DFS를 시작하냐에 따라 1개의 DFS Tree가 나올 수도, 여러개의 DFS Tree가 나올 수 있다.
Back Edge가 존재한다.
Forward Edge가 존재한다.
Left Cross Edge가 존재한다.
Right Cross Edge가 존재할 수 없다.
하나의 SCC는 반드시 단일 Tree 내에 존재한다.

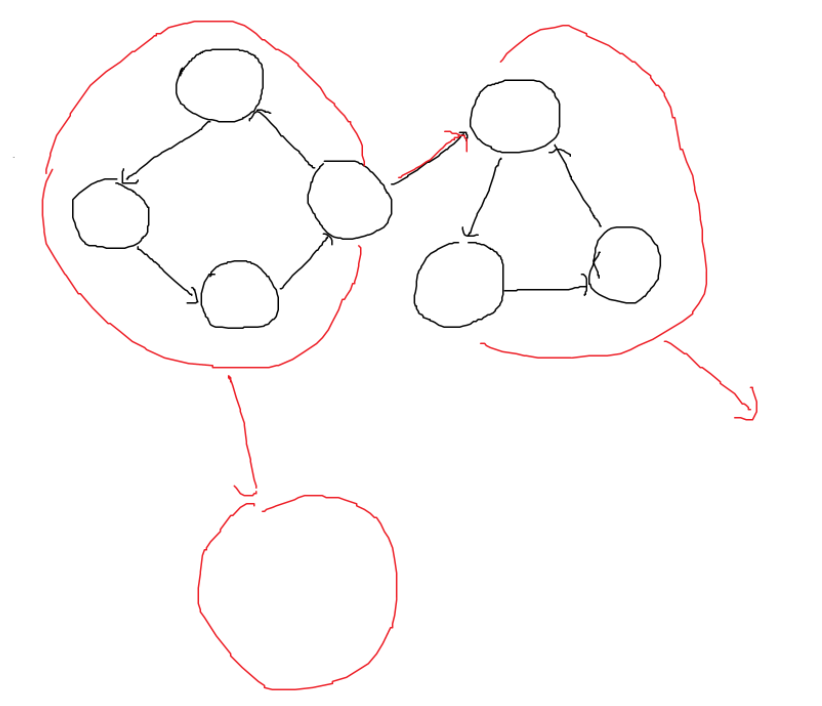
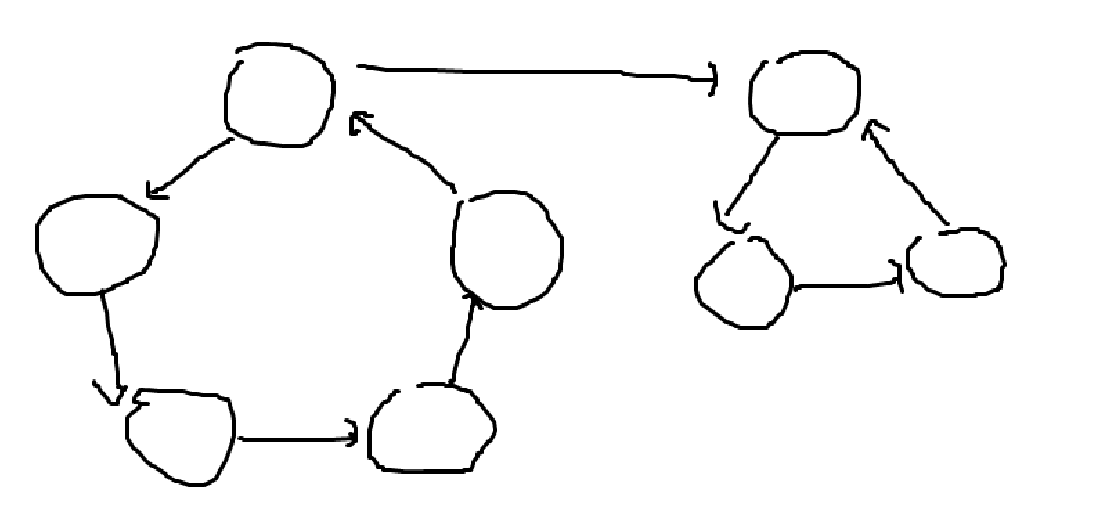
우리가 임의의 그래프에서 SCC들을 찾기 위해 사용할 성질은 1번과 6번이다. 만약 운이 좋게 시작 노드를 잘 선택하면, 한개의 DFS Tree당 한개의 SCC를 가지도록 할 수 있을 것이다. 만약 시작 노드를 잘 선택하는 방법을 안다면, DFS 한번당 SCC 한개를 뽑아내도록 만들 수 있다! 만약 위와 같은 그래프가 존재하면, 왼쪽에서 DFS를 시작하면 하나의 DFS Tree밖에 안만들어지지만 오른쪽에서 DFS를 시작하면 DFS Tree가 2개 만들어지고, 하나의 DFS Tree당 하나의 SCC를 갖게된다.

시작 노드를 어떻게 선택해야 하는가? Post Number를 사용하면 된다. 먼저 DFS를 한번 돌려서 Post Number를 붙이고, 이후 DFS Visit가 아직 안된 노드 중 Post Number가 가장 큰 Node를 시작노드로 잡아 DFS를 돌리면 된다. 이떄, 두번째 DFS에선 Graph의 Edge 방향을 Reverse해야 한다. 정리하면 다음과 같다.

일단 DFS를 돌리면서 Post Number를 붙인다.
모든 Edge (Links)를 Reverse한다.
DFS를 한번 더돌리는데, DFS를 시작할 때 Post Number가 가장 큰 곳에서 시작한다.

Supergraph

Supergraph라는 개념을 정의하자. 이는 하나의 SCC를 하나의 노드로 생각하여 만드는 그래프다. Supergraph는 알고리즘 구현할 때는 사용하지 않고, 순전히 이해를 돕기 위한 개념이다. Supergraph는 절대 Cycle이 존재할 수 없다. 왜냐하면, Cycle이 있으면 애초에 그것이 하나의 SCC가 되기 Supergraph 상에서는 하나의 노드로 표현되어야 하기 때문이다.

Supergraph는 DAG이고, DAG는 Indegree가 0인 노드에 Max post number가, Outdegree가 0인 노드 중에 Min post number가 있음을 알 수 있다. 최종적으로 목표가 무엇인가? DFS를 돌렸을 때 DFS Tree 안에 SCC가 하나만 존재하도록 시작 노드를 잘 정하고 싶다. 그것을 위해 Outdegree가 0인 노드에서 DFS를 시작하면 되고, Outdegree가 0인 노드는 Min post number를 통해 찾을 수 있다.

따라서 Min post number를 시작 노드로 잡으면 계속 DFS 한번당 하나의 SCC를 쏙쏙 찾아낼 수 있다. 반대로 Edge를 Reverse하면 Max post number를 시작 노드로 잡으면 된다. 이것이 생각하기 더 편할 수도 있다.

IT, 알고리즘