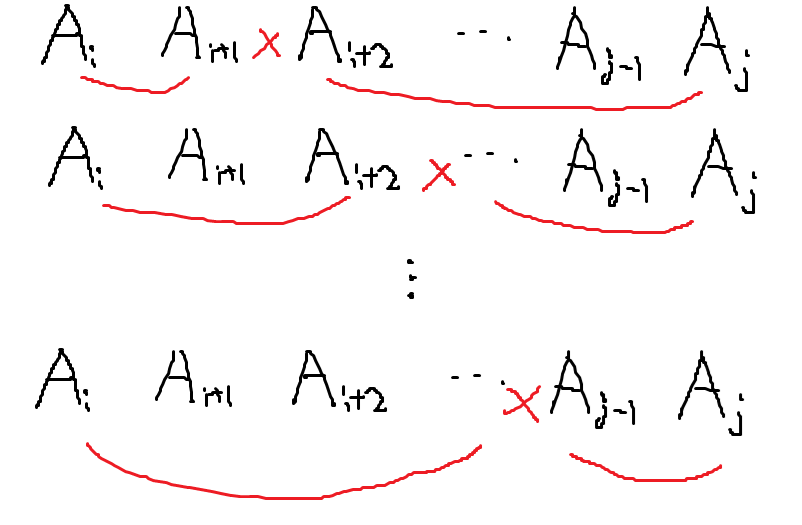알고리즘 4. Dynamic Programming

게시 2024/12/28 업데이트 2025/01/13

By 신희곤

60 분읽는 시간

건국대학교 알고리즘 김성열 교수님의 수업을 정리한 내용입니다.

Dynamic Programing

Dynamic Programing의 본질은 ‘기록하며 풀기’와 같다. 알고리즘이란 문제의 모든 경우를 일반적으로 해결하는 방법이다. 따라서 문제를 해결하기 위해 모든 경우를 다 따져봐야 하는데, 그 과정에서 중복되는 계산이 많이 생기면 배열과 같은 곳에 저장했다가 값을 재활용할 수 있다. 다이나믹 프로그래밍이 뜻하는 것은 그저 위의 사실이다.

문제가 재귀로 Top-down으로 풀린다면, Memoization 방법으로 최적화할 수 있다. 문제가 Bottom-up으로 풀린다면, Tabulation 방법으로 최적화할 수 있다.

재귀를 DP 점화식으로 바꾸기 위해선, 다음 Step을 거치면 된다.

Base Condition -> DP Table의 초기값 설정.
반환식 -> 점화식으로 바꾸고, 순차적으로 for looping.

[!tip]- DP는 문제를 딱 보고 ‘이거 DP로 풀어야겠다’ 이게 아니다. {title} 일단 다 해보고, 다 해봤더니 중복 계산이 많아서 DP로 최적화 시키면 되곘는데? 라는 사고 흐름으로 가야 한다.

DP로 문제를 풀었다면, DP Table에 적힌 패턴을 분석하여 더 최적화할 수도 있다. 이를 DP 최적화라고 한다.

Memoization

  
int Fibonacci(int n)
{
    if (n < 2) return 1;
    return Fibonacci(n-1) + Fibonacci(n-2);
}

재귀 도중 중복되는 계산이 많이 발생하면, 재귀의 결과를 테이블에 저장하여 재활용하면 된다.

  
int memo[]; memo[0] = memo[1] = 1;
int Fibonacci(int n)
{
    if (memo[n] != -1) return memo[n];
    memo[n] = Fibonacci(n-1) + Fibonacci(n-2);
    return memo[n];
}

Tabulation

  
int Fibonacci(int n)
{
    int fibonacci[n+1];
    fibonacci[0] = fibonacci[1] = 1;

    for (int i = 2; i <= n; i++)
    {
        fibonacci[i] = fibonacci[i-1] + fibonacci[i-2];
    }
    
    return fibonacci[n];
}

함수의 결과를 저장해야하기 때문에, DP 테이블의 차원 수는 함수의 입력값과 동일하다. 함수가 int Func(int a, int b) 꼴이라면 DP 테이블 또한 int func[a+1][b+1]와 같이 정의된다. Array의 Out of Bound와, 직관적인 해석을 위해 Zero-based가 아니라 1-based을 사용하면 좋다.

[!example]- Select Working Days{title}
하루마다 일했을 때 얻을 수 있는 이익 \(P[i]\)가 주어지고, 연속으로 일할 수 없다. 이때 가장 돈을 많이 벌 수 있는 스케쥴을 찾는 방법.
알고리즘이란 문제의 모든 경우를 일반적으로 해결하는 방법이다. 따라서 모든 경우를 다 따져보면 된다. 각 날마다 ‘일을 하는 경우’와 ‘일을 하지 않는 경우’가 존재한다. max(전날에 일을 했을 때 최대 이익, 전날에 일을 안했을 떄 최대 이익) 중 큰 것을 고르면 될 것 같다.
만약 Profit Array가 \([3, 5, 1, 2, 5]\)와 같이 주어지고, \(W[i]\) : i번째 날 일을 했을 때 최대 이익, \(N[i]\) : i번째 날 일을 안했을 때 최대 이익이라고 정의하면 다음과 같다. 스케쥴이 1일일 때
당일 일을 했을 때 최대 이익 : \(W[1]=P[1] = 3\)
당일 일을 하지 않았을 때 최대 이익 : \(N[1]=0\) 스케쥴이 2일일 때
당일 일을 했을 때 최대 이익 : \(W[2] = P[2] + N[1] = 5\)
당일 일을 하지 않았을 때 최대 이익 : \(N[2] = max(W[1], N[1]) = 3\) … 스케쥴이 i일일 때
당일 일을 했을 떄 최대 이익 : \(W[i]=P[i]+N[i-1]\)
당일 일을 할 때, 전날에는 반드시 일을 할 수 없다.
당일 일을 하지 않았을 때 최대 이익 : \(N[i]=max(W[i-1], N[i-1])\)
당일 일을 하지 않았을 때, 전날에 일을 하거나 일을 하지 않거나 두가지 경우를 모두 고려해야 한다.
당일 최대 이익 : \(max(W[i], N[i])\)
1 2 3 4 5 6 7 8 9 10 11 12 13 int maxProfit(int P[], int n) { int W[n], N[n]; W[0] = N[0] = 0; for (int i = 1; i <= n; i++) { W[i] = P[i] + N[i-1]; N[i] = max(W[i-1], N[i-1]); } return max(W[n], N[n]); }
결과를 계산하는 과정에서 이전의 모든 값을 활용하면 배열을 유지하면 되지만, 이번 계산은 딱 이전결과의 값만 사용하면 되므로, 배열에서 변수로 수정하면 공간복잡도를 \(O(n)\)에서 \(O(1)\)로 줄일 수 있다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int maxProfit(int profits[], int n) { int preWork = profits[0]; int preNonWork = 0; for (int i = 1; i < n; i++) { int currentWork = work[i] = preNonWork + profits[i]; int currentNonWork = max(preWork, preNonWork); preWork = currentWork; preNonwork = currentNonWork; } return max(preWork, preNonWork); }

[!example]- Path Counting{title}
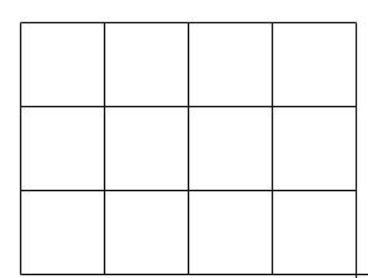
2차원 map이 있을 때, 왼쪽 위에서 출발하여 오른쪽 아래에 도착한다. 이때 가능한 모든 Path 개수를 구하는 방법.
모든 경우를 다 해보면 된다. 입력은 2차원 배열 \(M[n][m]\)이 주어진다고 하자. 그냥 함수가 \((i, j)\) 위치까지 올 수 있는 모든 경우를 반환한다면 재귀적으로 \(\text{return}~F(i-1, j) + F(i, j-1)\)을 하면 될듯? 만약 막혀있는 길이 있다면, 위와 왼쪽의 길이 막혀있는지 아닌지 체크하면 된다. Memoization을 쓰면 된다. DP를 쓰자면, \(D[i][j] = D[i-1][j] + D[i][j-1]\)을 하면 된다.
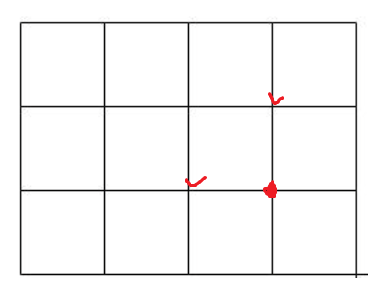
각 점까지 오는 모든 경로의 수를 담는 상태 배열 pathCount[n][m]를 정의하면, 그 위치로 올 수 있는 모든 경로의 경우의 수를 합하면 된다. 따라서 상태가 정의되고, 이전 상태의 결과만을 사용하여 현재 상태의 값을 계산해내므로 DP로 해결할 수 있다.
예를들어, 위와 같은 그림에서 해당 Point로 오는 경로의 개수는 왼쪽에서 오는 경우의 수와 위에서 오는 경로의 경우의 수의 합과 같다. 이때 값이 계산되는 순서 또한 중요하다. 만약 대각선부터 계산하게 되면 이전 경로의 값이 계산되지 않았으므로 DP를 수행할 수 없기 때문이다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 int pathCounting(int map[][], int n, int m) { int DP[n+1][m+1]; memset(DP, 0, sizeof(D)); // 외곽선부터 계산 for (int i = 1; i <= n; i++) DP[i][1] = 1; for (int j = 1; j <= m; j++) DP[1][j] = 1; // 내부 DP 계산 for (int i = 2; i <= n; i++) { for (int j = 2; j <= m; j++) { DP[i][j] = DP[i-1][j] + DP[i][j-1]; } } return DP[n][m]; }
그런데 이것도 결국 현재 행과 이전 행만 사용하므로, 공간 복잡도 \(O(nm)\)에서 \(O(m)\)으로 최적화가 가능할 것 같다. pathCount[n][m] 대신 preRow[m], currentRow[m] 두개를 사용하면 되지 않을까?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 int pathCounting(int map[][], int n, int m) { int preRow[m]; int currentRow[m]; for (int j = 0; j < m; j++) preRow[0] = 1; for (int i = 1; i < n; i++) { currentRow[0] = 1; for (int j = 1; j < m; j++) { currentRow[j] = preRow[j] + currentRow[j-1]; } copy(currentRow to preRow); } return currentRow[m-1]; }
Path Counting를 실제로 사용하는 경우가 바로 구글의 Page Ranking이다. 좋은 문서는 다른 곳에서 참조를 많이 하는 웹페이지일 것이라는 아이디어에 착안해, 그 웹페이지로 오는 Path Counting을 계산하여 랭킹을 매긴다.

[!example]- Matrix Multiplication{title} 여러 행렬을 곱하는 경우, 행렬 곱은 결합법칙이 적용된다. 어떤 행렬 곱을 먼저 하냐에 따라서 계산하는 횟수가 달라질 수 있는데, 이때 계산 양이 가장 작아지는 행렬 곱 순서를 구하는 방법.
예를들어, \(ABC\) 행렬곱을 하고, 각각 행렬 사이즈는 \(3\times 5, ~5\times 1, ~1\times 4\)라고 할 때 \((AB)C\)부터 계산하면 계산 횟수는 \(3 \times 5 \times 1 + 3 \times 1 \times 4 = 27\)번이고, \(A(BC)\)부터 계산하면 계산 횟수는 \(5 \times 1 \times 4 + 3 \times 5 \times 4 = 80\)번이다.
곱하는 행렬을 \(A_{1}, A_{2}, \dots, A_{n}\)라고 하고, \(A_{i}\) 행렬의 사이즈를 \(d_{i-1} \times d_{i}\)로 정의하자. 실질적인 입력값은 \(d_{0}, d_{1}, d_{2}, \dots, d_{n}\)이다. 모든 경우를 다 따져보면 된다. (i~i+1, i+2~j), (i~i+2, i+3~j), … (i~j-2, j-1~j) 행렬을 곱했을 때 결과가 가장 작으면 된다. 점화식으로 표현하면, \(DP[i][j] = min(DP[i][i+k] + DP[j-k][j]), ~~(1\leq k\leq j-i)\)를 계산하면 됨.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 int minCalculationCount(int d[], int n) { int DP[n][n]; for (int len = 2; len <= n; len++) { for (int i = 0; i <= n - len; i++) { int j = i + len - 1; DP[i][j] = INT_MAX; for (int k = i; k < j; k++) { DP[i][j] = min(DP[i][j], DP[i][k] + DP[k+1][j] + d[i-1] * d[k] * d[j]); } } } return DP[0][n-1]; }

[!example]- Maximum Subarray{title} 음수를 포함하는 배열에서 연속된 부분의 배열의 합이 최대가 되는 Subarray를 찾는 방법.
모든 경우를 다 해보자. i=0을 시작으로 갖는 Subarray의 합, i=1을 시작으로 갖는 Subarray의 합, …을 모두 해보면 \(O(n^2)\)이 걸린다. 이 방법은 (0, i)에서 Subarray의 합을 계산하는 것과 (2, i-2)에서 Subarray의 합을 계산할 때 중복되는 계산이 존재한다. 따라서 DP로 최적화가 가능할 것 같다.
Input Array를 A[i]라고 정의하고, DP[i]를 ‘i에서 끝나는 Subarray의 최대 합’으로 정의하자. DP[i]는 max(DP[i-1] + A[i], A[i])로 구할 수 있다. DP[i-1]은 i-1에서 끝나는 Subarray의 최대 합이다. i에서 끝나는 Subarray의 합은 DP[i-1] + A[i] 또는 A[i]인 경우밖에 없다. 둘 중 큰 경우를 선택하면 된다.
만약 Zero Elements Subarray를 허용한다면, DP의 점화식이 좀 다르다. DP[i-1] + A[i] 계산값이 음수라면 그냥 Zero Elements Subarray를 취하는게 이득이므로, 이 경우 DP[i]에 0을 저장한다. DP[i] = max(DP[i-1]+A[i], 0)

[!example]- Dijkstra{title} 다익스트라는 시작 노드와 음수가 없는 Weight Graph를 입력받으면, 각 노드마다 최단 경로를 찾아내는 알고리즘이다. 입력이 그래프라고 반드시 DP를 기록할 자료구조를 그래프를 써야되는 건 아니다. Dijkstra의 경우는 Priority Queue를 사용한다.
다익스트라도 DP라고 볼 수 있다. 시작 노드에서 출발하여 인접한 노드의 최선의 값을 계산하여 자료구조에 기록해둔다. 이후 큐에서 기록해둔 Value가 가장 작은 노드를 꺼내서 Directed Edge Weight와 기록한 Value를 비교하여 최단 경로를 확정한다. 즉 메모리에 값을 기록해두고, 기록해둔 값만을 사용하여 최적 값을 도출해내는 DP와 같다.

[!example]- All-Pairs Shorest Path{title} Weight Graph가 주어졌을 때, 모든 노드 쌍 간의 Shorest Path를 찾는 문제.
모든 노드에 대해 한번씩 다익스트라를 돌리면 \(O(n(n+m)\log n)\) 시간에 찾을 수 있다. 최악의 간선 개수는 한 노드가 모든 노드와 연결되어있을 때 \(m=n^2\)이므로 \(O(n^3\log n)\)이다. 만약 i 노드에서 j 노드로 가는 Shorest Path를 찾아두면 j 노드에서 계산할 때 i 노드로 가는 Shorest Path를 찾지 않아도 된다. 이런 중복 계산을 빼면 더 빨라지게 할 수 있을 것 같다.
모든 케이스를 따져보자. 그래프의 노드를 \(N_{i}\)라고 정의한다. \(N_{i}\)에서 \(N_{j}\)로 가는 길은 바로 연결되어 있거나, 1개의 노드를 거쳐서 가거나, 2개의 노드를 거쳐서 가거나, …, k개의 노드를 거쳐서 가는 방법이 있다. 노드의 총 개수를 \(n\)이라고 할 때, \(k=n\)까지 확장하면 \(N_{i}\)에서 \(N_{j}\)로 가는 모든 경우의 수를 찾을 수 있다. 그 경우의 수 중, 최단거리 min(…)를 취하면 된다.
DP[i][j] = i 노드로부터 j 노드로까지 가는 최단거리 그래프의 입력이 W[n][m]과 같이 배열로 주어진다면, DP[i][j] = W[i][j]로 초기화하여 i노드와 j노드가 Directed로 연결된 경우를 고려한다. k를 1부터 n까지 늘려가며 k개의 노드를 거쳐서 만드는 DP[i][j]를 계산한다. 두가지 Case가 존재한다. 기존의 경로로 가는게 최단거리이거나, 새로 추가된 노드 k를 거쳐서 가는게 더 빠른 경우이므로, min(DP[i][j], DP[i][k] + DP[k][j])를 통해 DP[i][j]를 계산해낼 수 있다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int DP[n+1][n+1](INF); int F(int W[n+1][n+1], int n) { // init for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) DP[i][j] = W[i][j]; for (int k = 1; k <= n; k++) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) DP[i][j] = min(DP[i][j], DP[i][k] + DP[k][j]); }

[!example]- Longest Common Subsequence (LCS){title}
두 문자열에서 공통적으로 나타나며, 순서를 유지하는 가장 긴 부분 수열을 찾아라. 꼭 연속일 필요는 없지만, 순서는 같아야 한다. 즉 LCS란 두 문자열에서 문자열을 제거해서 두 문자열을 같게 만들 수 있는 최장 Subsequence를 의미한다. 예를들어 ABASDFASFJ와 ASRKASRM의 LCS는 ASAS이다.
재귀로 날먹 가능한가? 입력은 두 문자열과, 두 문자열의 길이 n, m이 주어져야 한다. 모든 케이스를 따져보자. 만약 마지막 두 글자, \(S_{1}[n] = S_{2}[m]\)이라면 그저 \(LCS(n-1, m-1) + 1\)을 반환하면 된다. \(S_{1}[n] \neq S_{2}[m]\)인 경우, \(S_{1}[n]\)이 \(S_{2}[1...m-1]\)의 Subsequence의 끝에 들어갈 수 있거나, \(S_{2}[n]\)이 \(S_{1}[1..n-1]\)의 Subsequence의 끝에 들어갈 수 있을 수 있다. 따라서 max(LCS(n-1,m),LCS(n,m-1))을 반환하면 된다.
1 2 3 4 5 6 7 8 9 int LCS(string S1, string S2, int n, int m) { if (n ** 0 || m ** 0) return 0; // 끝의 두 문자열이 같으면 if (S1[n-1] == S2[m-1]) return LCS(S1, S2, n-1, m-1) + 1; return max(LCS(S1, S2, n-1, m), LCS(S1, S2, n, m-1)); }
입력값이 같으면 함수값이 항상 똑같으므로, 중복되는 계산을 DP로 최적화시킬 수 있겠다. S1[i] == S2[j]라면 DP[i][j] = DP[i-1][j-1]을 넣으면 되고, 아니라면 DP[i][j] = max(DP[i-1][j], DP[i][j-1])를 넣으면 된다.
재귀함수를 DP로 최적화하려면 다음 Step을 거치면 된다.
Base Condition -> DP Table의 초기값 설정.
반환식 -> 점화식으로 바꾸고, 순차적으로 for looping.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 int lcs(string S1, string S2, int n, int m) { int LCS[n+1][m+1]; // 1. Set Base Condition for (int i = 0; i <= n; i++) LCS[i][0] = 0; for (int j = 0; j <= m; j++) LCS[0][j] = 0; // 2. Recursion To For Loop for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { if (S1[i-1] == S2[j-1]) LCS[i][j] = LCS[i-1][j-1] + 1; else LCS[i][j] = max(LCS[i-1][j], LCS[i][j-1]); } } return LCS[n][m]; }

[!example]- 최대 공백 정사각형 (Largest Empty Square){title}
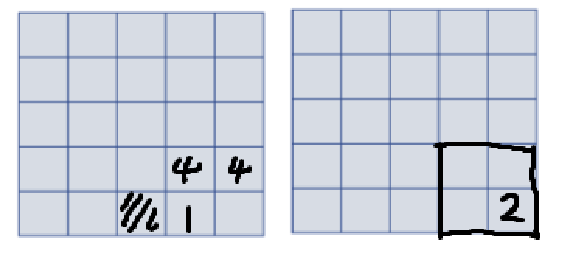
0과 1로 이루어진 2차원 배열이 주어질 때, 0으로 이루어진 가장 큰 정사각형을 찾는 방법.
재귀로 날먹할 수 있나? 함수의 입력값은 map[][]과 n, m이 주어져야 한다. 함수를 map[n][m]을 우측 하단 코너로 갖는 최대 정사각형의 크기라고 하면, \(LES(n-1, m)\)이 그릴 수 있는 최대 정사각형, \(LES(n, m-1)\)이 그릴 수 있는 최대 정사각형, \(LES(n-1, m-1)\)이 그릴 수 있는 최대 정사각형을 전부 체크해야 한다. 그 이유는, 셋 중 하나라도 작은 값이 있다면 중간에 채워진 값때문에 정사각형을 풀로 만들 수 없기 때문이다. 행, 열, 왼쪽 상단의 픽셀이 차있는지 비어있는지를 각각의 LES 이전값들이 보장하는 것이다.
1 2 3 4 5 6 7 int LES(int map[][], int n, int m) { if (n <= 0 || m <= 0 || map[n-1][m-1] == 1) return 0; return min(LES(map, n-1, m), LES(map, n, m-1), LES(map, n-1, m-1)) + 1; }
입력값이 같으면 출력값도 같기 때문에 중복되는 코드를 DP로 최적화할 수 있다. Base Condition을 DP Table 초기화로 바꾸고, 점화식을 DP[i][j] = min(DP[i-1][j], DP[i][j-1], DP[i-1][j-1]) + 1로 바꾸면 된다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 int LES_DP(int map[][], int n, int m) { int LES[n+1][m+1]; int maxSquare = 0; memset(LES, 0, sizeof(LES)); // 자동으로 기저 조건이 초기화됨. for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { if (map[i-1][j-1] != 0) continue; LES[i][j] = min(LES[i-1][j], LES[i][j-1], LES[i-1][j-1]) + 1; maxSquare = max(maxSquare, LES[i][j]); } } return maxSquare; }

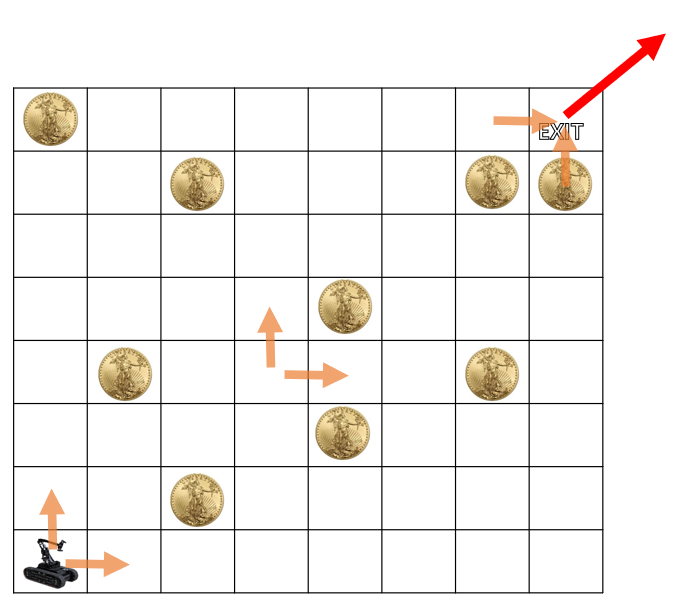
[!example]- 금화 모으기{title}
위와 같이 (0,0)에서 시작하여 (n,m)까지 갔을 때, 먹을 수 있는 최대 금화의 개수가 얼마인가? 재귀적으로 생각하면, (n,m) 위치에서 올 수 있는 위치가 왼쪽 또는 아래에서밖에 올 수 없다. max(Coin(n-1,m), Coin(n,m-1))에서 (n,m) 위치의 코인 여부를 더하면 된다
이를 DP Table로 정의하면, 점화식은 \(DP[i][j] = max(DP[i-1][j],DP[i][j-1]) + Coin[i][j]\)와 같다.

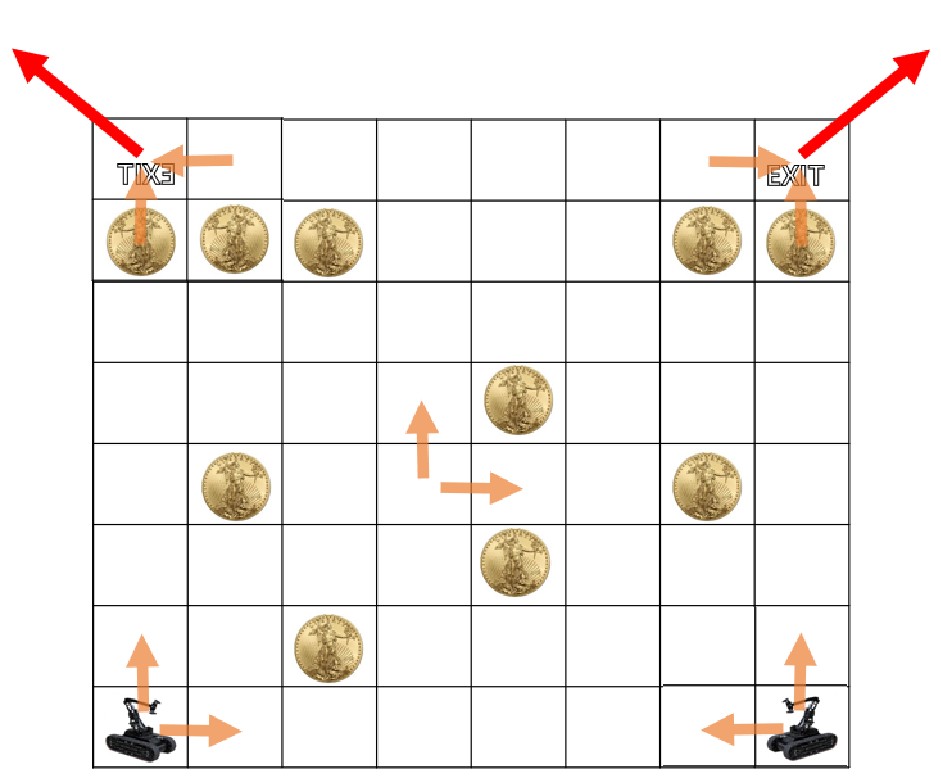
[!example]- 금화 모으기 (2명 버전){title}
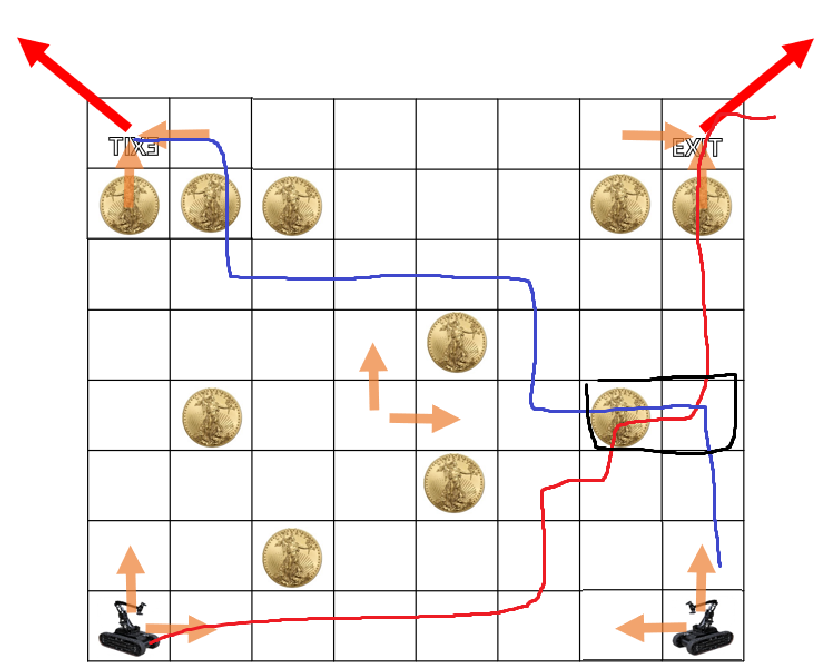
1명이 아닌 2명이서 금화를 먹는데, 한멍이 먼저 출발하여 ⬈ 방향으로 쭉 가서 코인을 먹고, 이후 다른 한명이 ⬉ 방향으로 가면서 코인을 먹을 때, 먹을 수 있는 코인의 총 합을 찾는 방법.
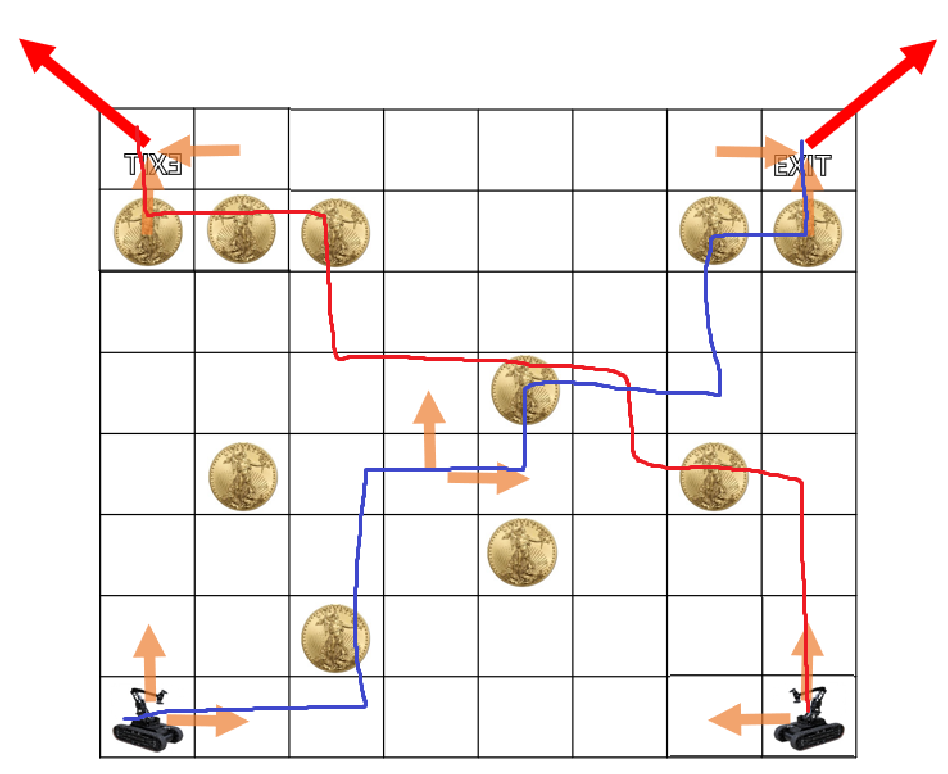
위 케이스는 갈 수 있는 수많은 경로중의 하나일 뿐이다. 어떤 특징을 찾을 수 있냐면, 두 경로는 반드시 ‘겹치는 부분’이 존재할 수 밖에 없다는 것이다. 한번 두 경로가 겹치는 구간을 생각해보자.
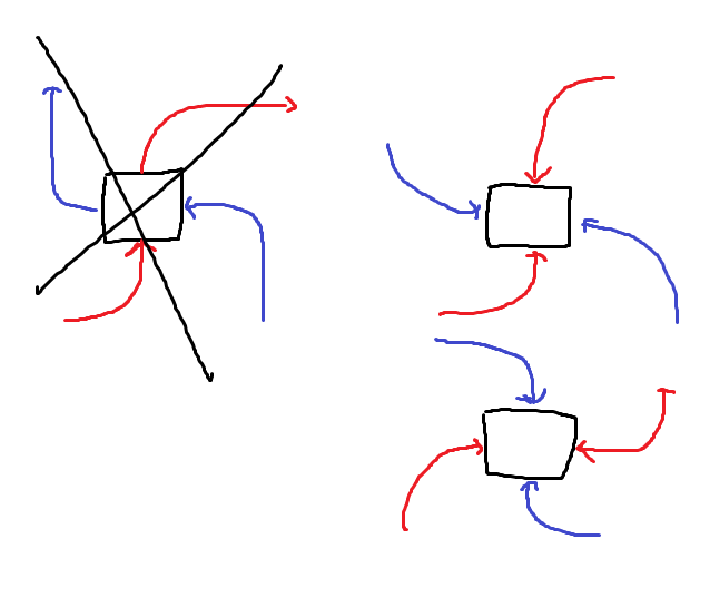
만약 위와 같이 겹친 경우를 생각해보자. 만약 들어가는 경로에서 왼쪽에 코인이 있다면, 그걸 먹고 가는게 더 이득이다. 답이 계속 갱신되며, 최종적으로 딱 한칸만 겹치는 경우가 최대 이득이 된다. 그렇다면, ‘어느 칸에서’ 딱 겹치는게 가장 이득일까? 이건 잘 모르겠고, 이련 경우 모든 칸에 대해서 다 따져보는 수밖에 없다.
다행인 점은, 사이드에서 딱 한칸만 겹치는 경우는 없다는 것이다. 사이드에서 겹치는 경우, 항상 최소 두칸 이상 겹칠 수 밖에 없다. 따라서 Zero-based를 기준으로 (1, 1)부터 (n-2, n-2)칸을 따져보면 된다.
생각의 편의성을 위해 한명이 경로를 따라 쭉 가는게 아니라, 두명이 코인을 먹다가 가운데에서 딱 만났다고 생각하자. 그렇게 해도 문제 상황은 동일하다. 케이스가 오른쪽 그림과 같이 두가지밖에 없으므로, 두 케이스 중 더 큰 케이스를 취하면 된다. (구현은 생략)

[!example]- 금화 모으기 (2명 + 음수 포함 버전){title}
만약 음수 칸이 존재해서, 그 칸을 지나가는 경우 어떻게 될까? 하나만 가는건 똑같이 풀리고, 두명이 먹는 경우는 좀 다르다.
딱 한칸만 먹는게 제일 좋다는 논리가 적용될 수 없다. 왜냐면, 그 경로가 아니라 다른 쪽을 먹는게 더 손해인 경우가 생기기 때문이다. 그럼 가로로 1칸, 2칸, 3칸, …, n칸 겹치는 거 중 답이 존재한다. 이를 따지는데 \(O(n^2)\)이 걸리고, 세로까지 확장하면 \(O(n^3)\)에 풀 수 있다. 이를 \(O(n^2)\)으로 풀 수 있을까? 만약 1, 2, 3, …n칸 겹치는거중 가장 좋은게 k칸 겹치는걸 찾았다고 해보자. k칸 겹치는게 가장 베스트라는 이유는, 뒤에 칸을 더 추가하거나 삭제하는게 더 손해라는 뜻이다. 뒤에 칸을 더 추가하는게 손해라는 뜻은, ..? 핵심은 뒤에 한칸을 추가하고 앞에 한칸을 빼도 최대최소 그래프가 위아래로 움직이기만 하지 그 위치는 변하지 않아 n을 하나 뗄 수 있다?

[!example]- 동전 거스름 돈{title} N원의 거스름 돈을 돌려줄 때, 최소 개수의 동전을 사용하여 거스름돈을 돌려주는 방법을 구하시오. 동전은 1, 4, 6원이라고 하고, 동전의 개수는 충분하다고 가정한다. 만약 거스름 돈의 종류가 2배 이상이 되면 그리디 작전으로 풀 수 있다. 큰 단위의 거스름돈을 먼저 거슬러주고, 이후 큰 단위 순서대로 계속 거슬러주면 된다. 하지만 거스름돈 단위가 2배수 이상이 아니라면, 그리디 작전이 먹히지 않는다. 그 이유는, 반례가 있기 때문이다. 예를들어 거스름돈 단위가 1, 4, 6원이고 8원을 거슬러줘야할 때 그리디 작전을 쓰면 6, 1, 1 원을 거슬러준다. 하지만 정답은 4, 4원이기 때문이다.
풀이법은 그냥 현재 금액에서 -1, -4, -6 해봤을 때 가장 작은 경우를 반환하는 경우를 재귀적으로 찾아서 반환하면 되겠다.
1 2 3 4 5 6 7 int change(int money) { if (money == 0) return 0; if (money < 0) return INF; return min(change(money-1), change(money-4), change(money-6)) + 1; }
메모이제이션으로 바꾸면 다음과 같다.
1 2 3 4 5 6 7 8 9 10 11 12 int C[10001]; int change(int money) { if (money == 0) return 0; if (money < 0) return INF; if (C[money] != -1) return C[money]; int result = min(change(money-1), change(money-4), change(money-6)) + 1; C[money] = result; return result; }

[!example]- Longest Increasing Subsequence (LIS){title} 숫자 배열이 입력될 때, 증가하는 가장 긴 Subsequence를 찾는 방법.
[!error] 시행착오{title} 함수 자체를 숫자 배열과 배열의 크기를 입력하면, 가장 긴 Subsequence의 길이와 가장 큰 숫자를 반환하면 됨. 재귀적으로 LIS(n-1) 값을 얻어내서 \(LIS(n-1).max < A[n]\)이 성립하면 \(LIS(n-1).len+1\) 반환하면 되는거고 아니면 그대로 \(LIS(n-1)\) 값을 반환하면 된다.
어 그런데 단순히 딱 -1인 경우만 되는게 아니라 다른 모든 경우와 비교해봐야하는데? 즉 1부터 i-1까지 Loop도는 Index를 j라고 하면, \(A[j]<A[i]\)일 때 \(LIS[i] = max(LIS[i], LIS[j]+1)\)을 모두 체크해봐야 함. 이 방법은 \(O(n^2)\)의 시간이 걸린다.
DP 최적화란, DP로 문제를 일단 풀어보고 저장된 데이터들의 값의 패턴을 분석하여 더 빠르게 최적화하는 기법이다. LIS의 DP Table을 분석하여 DP 결과를 최적화 해볼 수 있다. 위 Table은 1행이 Value값이고, 2행이 DP Table에 저장된 최장 Subsequence 길이다. 가만 들여다보면 패턴을 찾을 수 있다. 나보다 작고, 가장 가까운 Value값의 LIS 값만 알면 된다. 예를들어 3의 경우 ‘나보다 작고 가장 가까운 Value’값은 2고, 2의 LIS값이 1이므로 1+1=2가 저장된다.
각 길이값마다 가장 작고, 가장 최신인 Value 값만 알고있으면 된다. 따라서 길이 값이 Index이고, Value는 가장 최신으로 갱신된 Value 값을 저장하는 Array를 하나 정의한다. 이것을 Remember Array라고 부르자. 이 Array는 Index가 클 수록 더 큰 Value값이 올 수 밖에 없다. 만약 Index가 더 작은데 더 큰 Value값이 왔다고 가정해보자. 현재 Index값은 “해당 Value값 위치에서 가장 긴 Subsequence의 길이”를 뜻한다. 8과 10이 어느 순서로 배치되어 있었는지 알 수 없다. 따라서 8이 먼저 오는 경우, 10이 먼저 오는 경우 둘다 따져보자.
index value
4
3 8
2 10
1
1) 8, …, 10 이 경우 8 앞에 8보다 작은 숫자 3개가 반드시 존재하고, 10이 8보다 뒤에 있으므로 10의 길이는 최소 3 이상이어야 하므로 모순이다.
2) 10, …, 8 이 경우는 지금까지 최장 길이가 2인 최소 꼬리값이 10보다 작은 값이 없다는 뜻이다. 또, 8의 최장길이가 3이라는 뜻은 8보다 작은 값이 앞에 3개는 있어야 한다는 뜻이다. 8보다 작은 세 값중 가장 큰 값은 최장 길이가 2다. 이 값은 10보다 확실히 작으므로, Index=2에는 10이 아닌 다른 값이 적혀야 한다. 따라서 모순이다.
index value
6 -
5 25
4 15
3 10
2 8
1 2
Remember Array는 반드시 정렬되어 있고, 정렬되어있는 Array에는 Binary Search 사용이 가능하다. 만약 12라는 값의 LIS를 찾고싶다면, Remember Array에서 바이너리 서치를 한다. 그러면 15또는 10을 찾을 수 있다. 어떤걸 찾느냐는 구현 방식에 따라 원하는 것을 택할 수 있다. 12는 꼬리 Sequence가 10인 Max Sequence 뒤에 붙일 수 있으므로, 12의 LIS Size는 4다. 따라서 Index 4의 값을 12로 갱신해주면 된다.

index	value
4
3	8
2	10
1

index	value
6	-
5	25
4	15
3	10
2	8
1	2

Approximate String Matching

String Matching이란, 주어진 문자열에서 특정 문자열이 존재하는지 찾아내는 것이다. Approximate String Matching이란, 주어진 문자열에서 찾고 싶은 문자열과 비슷한 문자열이 존재하는지 찾아내는 것이다. 그것을 알기 위해, 두 문자열이 있을 때 두 문자열이 얼마나 비슷한지를 판단하는 척도가 필요하다. 그 척도는 다음과 같다.

Hamming Distance
Edit Distance
Weight Edit Distance

Hamming Distance는 각 자릿수의 문자열이 서로 같은지 다른지 비교하여, 다를 수록 Distance가 크다고 판단한다. 두 문자열의 길이가 같아야 하고, 한칸만 밀려도 100% 다른 문자라고 인식되는 단점이 존재한다. Edit Diestance는 한 문자열을 다른 문자열로 변경하기 위해 필요한 Edit Operation의 최소 개수이다. Edit Operation은 Insert, Delete, Change 세가지가 있다. Weight Edit Distance는 문자마다 가중치를 부여하는 것이다. s를 d로 잘못치는게 s를 p로 잘못치는 것보다 더 빈번하고, 이를 고려하기 위해 가중치를 부여하는 것이다.

[!example]- Minimum Edit Distance{title} 한 문자열을 다른 문자열로 변경하는 경우의 수는 무지하게 많다. 예를들어, ab를 abb로 바꾸기 위해 abc->abcc->abc->abb 와 같은 Case도 가능하기 때문이다. 하지만 우리가 필요한건 최소 Edit Distance다. 따라서 최소 Edit Distance를 찾는 알고리즘을 찾아야 한다.
Source 문자열의 길이를 \(n\), Target 문자열의 길이를 \(m\)이라고 할 때 Source 문자열을 \(S[1 .. n]\), Target 문자열을 \(T[1 .. m]\)이라고 정의한다. 시간 복잡도가 \(O(nm)\)이면 괜찮을 것 같다. 입력이 \(nm\)이기 때문이다. 알고리즘이란 문제의 모든 경우를 일반적으로 해결하는 방법이다. 따라서 모든 케이스를 따져보자. 재귀적으로 풀어보면, Case가 총 4가지다. 만약 \(S[n] \neq T[m]\)이라면 (1) Source 문자열에서 하나를 빼거나, (2) Source 문자열에서 하나를 더하거나, (3) Source 문자열을 바꾸는 경우가 있다. \(S[n] = T[m]\)이라면, (4) 아무것도 하지 않아도 된다. 따라서 \(F(n-1, m) + 1\), \(F(n,m-1) + 1\), \(F(n-1,m-1)\), \(F(n-1, m-1) + 1\) 중 최솟값을 취하면 된다. 이 재귀 코드는 입력값이 같으면 출력값이 같다. 따라서 DP를 사용해서 계산 결과를 재활용하면 되겠다.
1 2 3 4 if (S[i] == T[j]) DP[i][j] = DP[i-1][j-1]; else DP[i][j] = min(DP[i-1][j] + 1, DP[i][j-1] + 1, DP[i-1][j-1] + 1);
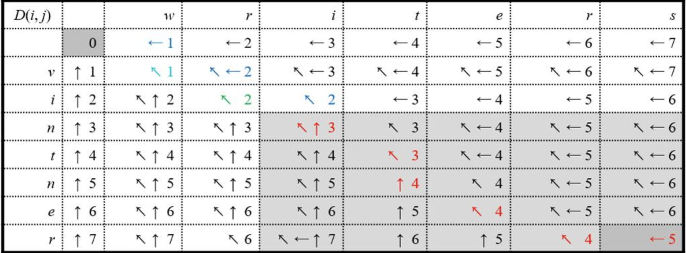
만약 문제가 경로 또한 구해야 한다면, DP 테이블을 저장하는 과정에서 값 뿐만 아니라 어떤 경로를 통해 불러왔는지 방향값도 저장해둔다. 이후 끝에서 시작하여 점화식을 역추적하면 된다. 이를 Backtrace라고 부른다. 만약 값과 방향값까지 적용한다면 Table이 아래와 같이 채워질 것이다.

[!example]- Dynamic Edit Distance Table{title}
Approximate String Matching 과정을 하기 위해서는, 긴 문자열에서 찾고싶은 문자열을 하나하나 비교해가면서 Matching하면 된다. 예전 String Matching할 때와 같이 그냥 긴 문자열의 처음부터 시작해서 한칸씩 밀어가면서 비교하면 되는데, 이러면 중복계산이 많이 발생한다. 이를 해결하는 알고리즘이 KMP가 있었다. KMP는 Matching 실패 시 딱 한칸을 미는게 아니라, 텍스트의 패턴 여부를 확인하여 시작 위치를 효율적으로 조절하는 알고리즘이었다. Approximate String Matching의 경우 비슷한 논리를 사용하기는 어려울 것 같다.
어떻게든 Source 문자열과 Target 문자열의 DP Table을 구했다고 치자. 만약 Target 문자열에 문자 하나가 추가된 경우, 처음부터 DP Table을 다시 계산하는 것은 아주 비효율적이다. 따라서 Target 문자열 뒤에 문자가 하나 추가되거나, Target 문자열 앞에 문자가 하나 삭제될 때 DP Table이 어떻게 바뀌며, 어떻게 업데이트해야하는가? 가 문제의 핵심이 된다.
Target 문자열 뒤에 문자가 추가되는 경우는 문제가 되지 않는다. 이미 \(DP[1..n][1..m]\) 값을 모두 알고 있기 때문에 이것을 활용하여 \(DP[n][m+1]\)를 구하는건 기존의 점화식을 쓰면 되기 때문이다.
문제는 Target 문자열 앞에 문자가 삭제되는 경우다. DP Table의 모든 값은 앞의 값에 의존하고 있기 때문에 앞의 문자가 하나 삭제되면 뒤의 문자가 전부 영향을 받을 수 있다.
이미지 압축 방식을 통한 아이디어를 얻는다. 이미지 압축의 원리는 이미지 픽셀 주변의 차이값을 기록한다. 픽셀 사이의 차이값은 그렇게 크지 않기 때문에, 적은 바이트로도 이미지를 표현할 수 있게 된다. 똑같이 최초에 한번 D Table을 생성한다. 이후 D Table을 DR Table로 변환한다. DR Table은 DR Table은 주변 칸과의 차이값만을 기록해둔 Table이다. 즉 각 칸마다 나와 위의 칸, 왼쪽 칸, 대각선 위의 칸과의 차이 3개(구조체)를 기록한다. 이후 어떤 열을 제거한다면 그 열과 인접한 셀들의 값들이 바뀌어야 할 것이다. 그 바뀌는 차이값만 따라가서 업데이트하면 Table의 값 전체를 Update하지 않아도 된다.

최대 공백 직사각형

잘 모르겠다

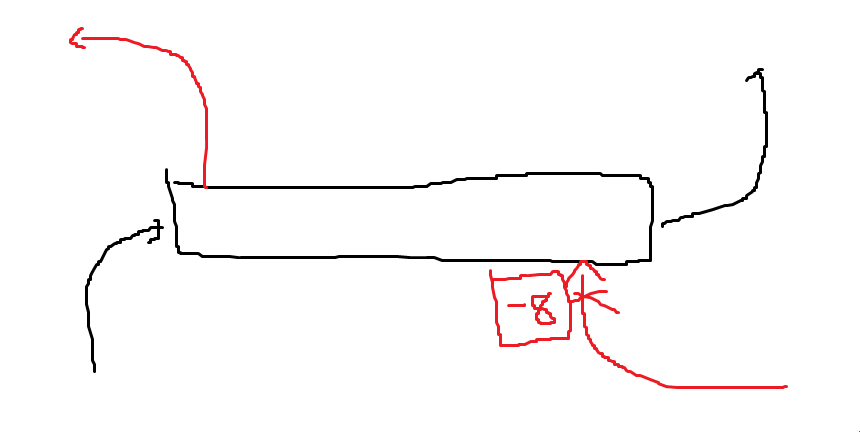
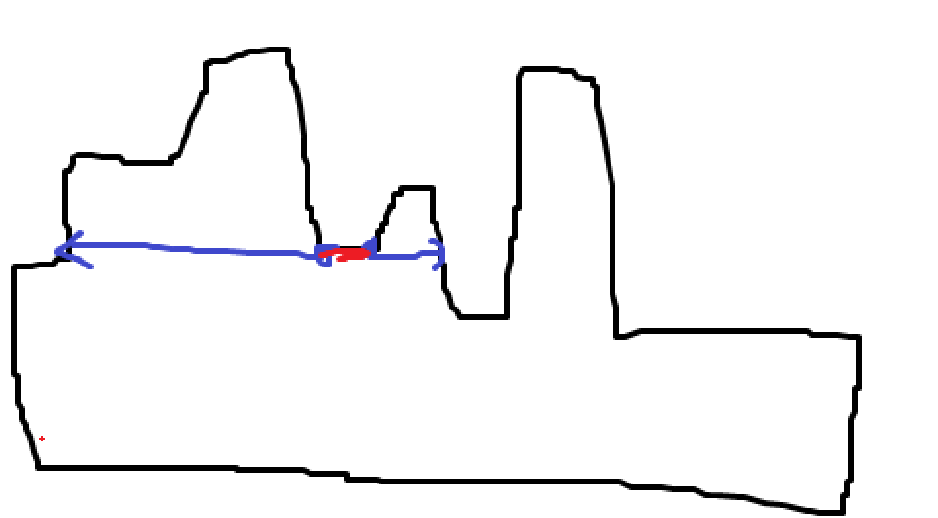
만약 위와 같은 모양의 막대 모양에 들어갈 수 있는 가장 큰 직사각형은 뭘까? 만약 정답이 있다면, 좌우나 상하로 늘릴 수 없다. 따라서 정답은 아래에 몰려있을 것이다.

만약 저 빨간색 선분에 닿도록 정답을 만드려면, 한쪽점에서 반대쪽에 닿을떄까지 쏴야한다. 또 오른쪽 점에서 반대쪽에 닿을떄까지 쏴야한다. 만약 한쪽이 막혀있다면 쐇는데 0인것과 같다.

선분 개수를 찾아서 따져보면 답을 구할 수 있겠다. 수평 선분은 최대 n개 올수 있으므로 선분을 잘 찾기만 하면 \(O(n)\)에 풀릴수도 있겠다.

저 꺾이는 점만 찾으면 선분을 찾겠는데, 꺾이는 점을 어떻게 빠르게 찾을까?

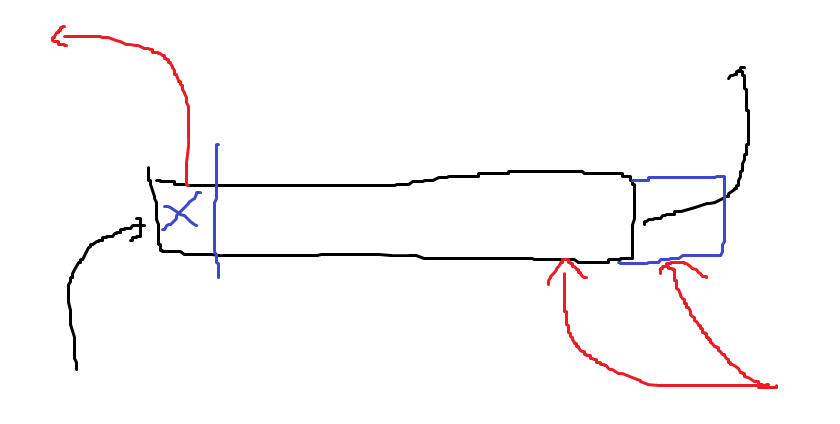
Convex Hull에서 하듯이 오른쪽에서 왼쪽으로 스위핑한다.

스택을 쓰면서 점을 스택에 추가한다. 내려가는 과정은 버리고, 올라가는 과정에선 점을 스택에 추가한다. 또 다시 내려가면 자신의 점이 나올때까지 점을 버린다.

만약 저렇게 파란점을 봤다면, 그위쪽에 있는 점은 의미없다. 다음부턴 왼쪽에서 쏜다면은 이미 저 쏜 언덕에 가려져서 그 위쪽은 안보이기 떄문이다.

실제 문제에선 수평선 하나를 쭉 긋고 각 점마다 최대 높이를 따져보면 똑같은 모양이 나옴. 이후 윗줄 입력의 답을 찾아내면 아랫줄 한줄 늘리는거는 빠르게 찾을 수 있음. 장애물 만나면 0으로 바꾸고 아니면 +1 늘리면 된다.

직사각형 찾는데 걸리는 시간 n, 그걸 n번 내려가므로 \(n^2\)에 풀린다.

완전 정보 게임

플레이어가 게임 내 상황을 전부 알고있다면 완전 정보 게임이다. 예를들어 바둑, 체스, 오목 등이 있다. 따라서 완전 정보 게임에서는 상대가 어떤 선택지를 할 수 있는지 다 알 수 있다. 포커, 가위바위보와 같이 플레이어가 게임 내 상황을 전부 알지 못한다면 완전 정보 게임이 아니다.

NIM 게임

처음에 돌이 K개 존재하고, 돌을 번갈아가면서 1, 2, …, i개씩 뺄 수 있을 때 상대방이 돌을 가져갈 수 없게 만든다면 승리하는 게임이다. 베스킨라빈스31, 바둑돌 가져가기 게임이 이에 해당한다. NIM 게임은 완전 정보 게임이고, 완전 정보 게임의 특징은 상대가 어떤 선택지를 할 수 있는지 전부 알 수 있다. 이론상 모든 케이스를 다 따져봐서 두 플레이어가 항상 최고의 선택지만 고른다면, NIM 게임의 승부는 시작부터 누가 이길지 결정되어 있다.

앞으로 얘기할 ‘이기는 선택지‘란 골랐을 때 상대가 패배 상태가 되는 선택지다. ‘패배 상태‘란 현재 상태에서 내가 어떤 선택지를 골라도 ‘상대에게 이기는 선택지‘가 존재하는 경우이다.

예를들어, 한 턴에 돌을 1, 3, 4개씩 가져갈 수 있다고 하자. 아래 Table은 현재 상태에서 Index 개수만큼 돌이 있을 때가 내 차례라면, 이기는지 지는지를 계산한 Table이다.

내 차례에 돌이 0이라면 게임 규칙상 패배한다. 내 차례에 돌이 1개라면 1개를 가져가면 상대를 ‘패배하는 상태’로 만들 수 있다. Win. 내 차례에 돌이 2개라면 나는 1개를 가져가는 선택지 밖에 없다. 그런 경우 다음에 상대가 1을 가져가면 내가 패배한다. 즉 어떤 선택지를 골라도 상대가 내게 Lose 상태를 넘겨줄 수 있기 때문에 Lose. 내 차례에 돌이 3개라면 3개를 가져가면 상대가 Lose한다. Win. 내 차례에 돌이 4개라면 4개를 가져가면 상대가 Lose한다. Win. 내 차례에 돌이 5개라면 3개를 가져가면 상대를 상대가 Lose한다. 내가 3개를 가져가면 상대에게 2개가 들어가는데, 내 차례에 2개가 오면 Lose인건 앞에서 계산한 내용이다. Win. 내 차례에 돌이 6개라면 4개를 가져가면 상대가 Lose한다. 따라서 Win. 내 차례에 돌이 7개라면 1, 3, 4개를 가져가면 각각 돌이 6, 4, 3개 남는데 이건 모두 상대가 이기는 선택지다. 따라서 내가 진다. Lose. 내 차례에 돌이 8개라면 1개를 가져가면 상대에게 Lose 상태를 넘겨준다. Win. …

NIM 게임은 앞의 결과를 이용해서 게임의 승패를 결정할 수 있다. 따라서 승부가 결정되어 있다. 구현도 DP로 모든 선택지를 다 따졌을 때 상대방을 지게만드는 법이 있다면 내가 이기고, 없다면 내가 지도록 구현도 가능하다.

NIM 게임 - 비대칭의 경우

NIM 게임인데, 본인이 가져간 돌 개수를 점수라고 하자. A는 본인의 점수를 최대화 하는게 목적이고, B는 A의 점수를 최소화 하는게 목적이다. 규칙이 다음과 같을 때, A가 얻는 최대 바둑돌 개수를 구하라.

순서가 있는 돌 더미들에서 A가 돌 더미 하나를 가져간다.
B는 A가 가져간 돌더미 왼쪽의 모든 돌 더미를 없애거나 오른쪽의 모든 돌 더미를 없앨 수 있다.
돌이 안남을 때까지 반복한다.

State Space Tree를 생각해볼 수 있다. 돌 더미가 \(n\)개가 있고 각 돌 더미에 들어있는 돌의 개수가 \([a_{1}, a_{2}, \dots, a_{n}]\)로 주어진다고 하자. 초기에 A는 \(a_{1}, a_{2}, \dots, a_{n}\)중 하나를 고를 수 있다. \(A\)가 어떤 값을 골랐을 때 최댓값을 반환하는 함수를 \(M(a_{i})\)라고 하자. A가 얻을 수 있는 최댓값은 \(max(M(a_{i})), (1\leq i\leq n)\)이다. A가 어떤 값을 골랐을 때 A가 얻게되는 최소 돌의 개수를 반환하는 함수를 \(m(k,\{L,R\})\)라고 하자. 인자값으로 L 또는 R을 넘겨줄 수 있다. 따라서 B가 골라야 하는 선택지는 \(min(m(k, L), m(k, R))\)과 같다. M 함수에서는 m을 호출하고, m 함수에선 M 함수를 호출하여 Base Condition까지 재귀호출되는 구조로 구현할 수 있다. 하지만 계산량이 너무 많고, Game State Array를 계속 수정해야 하는 단점이 있다. DP로 구현 가능할까?

\(a_{i}, a_{i+1}, \dots, a_{j}\)의 돌이 있을 때 A가 얻는 최대 돌의 개수를 \(M[i][j]\)에다 기록하고, A가 k번째 돌을 선택했을 때 A가 얻게 되는 최소 돌의 개수를 \(m[i][j][k]\)에 기록하자. 각각의 점화식을 \(M[i][j] = max(m[i][j][k])\), \(i\leq k\leq j\)과 \(m[i][j][k] = min(M[i][k-1], M[k+1, j]) + a_{k}\)로 계산할 수 있다. i, j, k가 모두 Loop를 돌기 때문에 시간 복잡도가 \(O(n^3)\)이다. DP 최적화를 할 수 있을까?

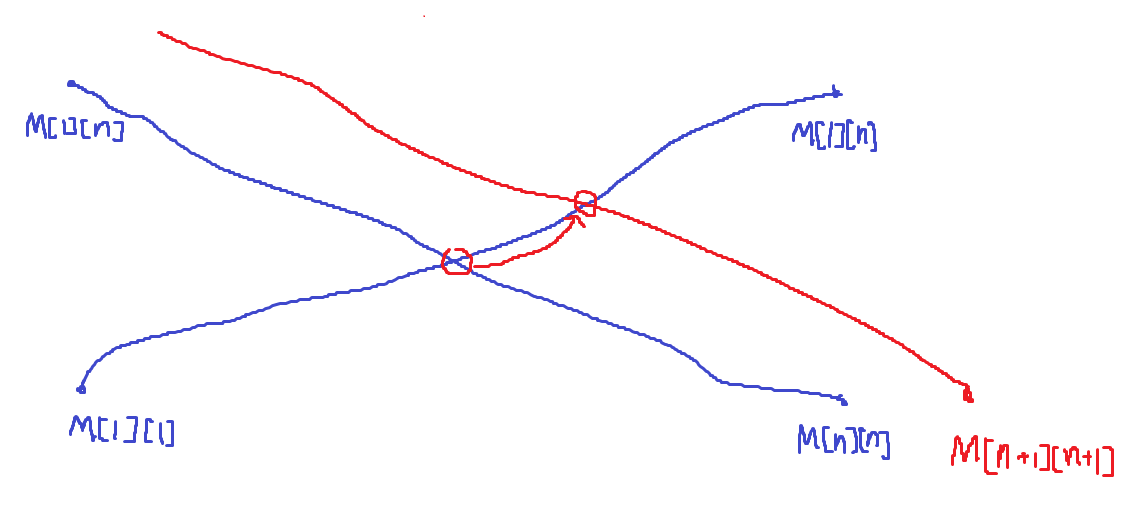
DP 최적화를 하려면, DP Table에 기록된 패턴을 파악해야 한다. 만약 \(i\)를 고정하고 \(j\)를 하나씩 늘리는 경우를 생각해보자. 이는 \(a_{i}, a_{i+1}, \dots, a_{j}\)의 답을 알고있을 때, 오른쪽에 \(a_{j+1}\)을 하나 추가한 것과 같다. 오른쪽에 \(a_{j+1}\) 돌을 추가했을 때 A가 얻는 최대 돌의 개수는 원래 알고있던 답보다 작아질 수 없다. 왜냐하면, \(a_{j+1}\)을 무시하고 원래 경로대로 돌을 먹으면 최소 원래 얻은 돌의 개수만큼은 보장되기 때문이다. 따라서 \(a_{j+1}\) 돌을 오른쪽에 추가하는 경우 원래 알고있던 답보다 같거나 커질 수 있고, 항상 \(M[i][j] \leq M[i][j+1]\)가 성립한다는 패턴을 하나 찾아낸다. 이번엔 반대로 j를 고정하고 i를 하나씩 줄이는 경우를 생각해보자. 이는 \(a_{i}, \dots, a_{j}\)의 답을 알고있을 때 왼쪽에 \(a_{i-1}\)를 하나 추가하는 것과 같다. 왼쪽에 돌을 추가하는 경우도 완전히 대칭이고, 항상 \(M[i-1][j] \geq M[i][j]\)가 성립한다는 것을 알 수 있다.

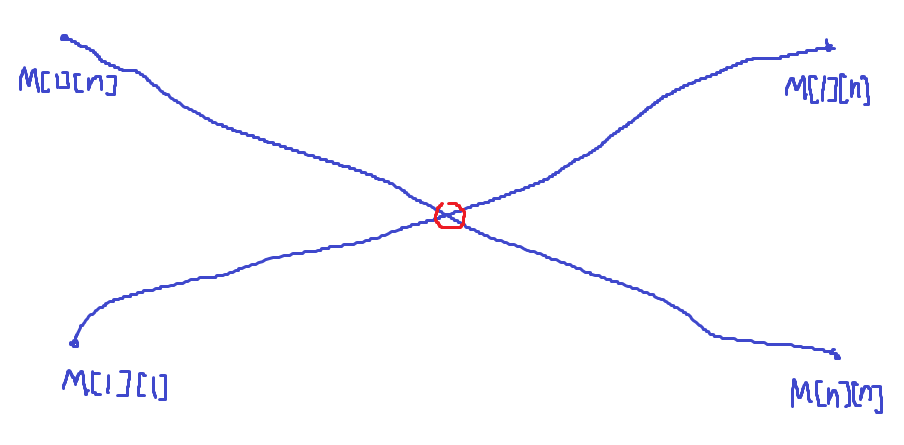
그래프를 그려보면 다음과 같고, 교점찾는 문제로 바뀐다. 배열이 정렬되어 있으므로, 바이너리 서치를 사용해서 교점을 찾을 수 있을 것이다. 따라서 \(N^2\)에 바이너리 서치 \(\log n\)이므로 총 시간은 \(O(N^2\log n)\)가 걸린다.

만약 오른쪽에 돌 무더기가 추가되면, j를 고정시키고 i를 감소시키는 그래프가 오른쪽으로 이동하고, 교점 또한 오른쪽으로 이동한다. 기존의 교점 위치를 기억하고, 동적으로 교점 위치를 계산하면 바이너리 서치하는 시간이 제외되고 총 시간 복잡도는 \(O(N^2)\)까지 줄어들게 된다. 교점은 그냥 한칸씩 증가시키면서 찾으면 되고, Amortization 아이디어가 적용되어서 시간을 크게 사용하지 않는다. 구현은 아주 어렵다.

IT, 알고리즘