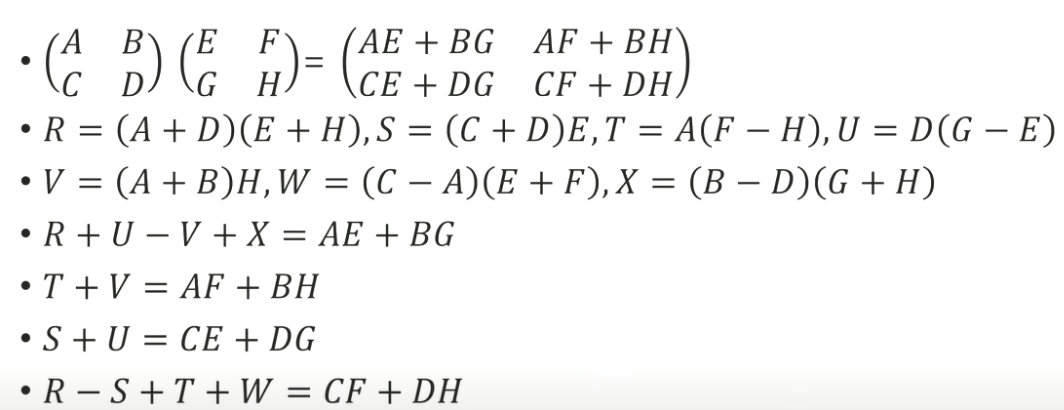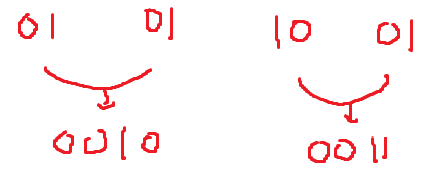알고리즘 3. Divide and Conquer

건국대학교 알고리즘 김성열 교수님의 수업을 정리한 내용입니다.

Divide and Conquer

입력값을 절반으로 나눠서 재귀적으로 답을 구했다고 치자. 두 답을 합쳐서 반환할 답을 만들 수 있다면 Divide and Conquer로 문제를 해결한 것과 같다. 정리하면 다음과 같다.

1. 입력 값을 나눈다. (보통 절반)
2. 각각 재귀적으로 답이 나왔다고 치자.
3. 양쪽에서 나온 답을 비교하여 새로운 답을 만들 수 있으면, Problem 해결!

알고리즘 1. Basic Algorithm#Merge Sort가 Divide and Conquer 방법을 적용한 Sorting 방법이다.

Quick Sort

Quick Sort는 기준으로 잡는 \(p\) 값에 따라 알고리즘이 느려질 수도 있고 빨라질 수도 있다. 만약 \(p\)를 잘 고를 수 있다면 Sorting 성능을 개선할 수 있을 것 같다. \(p\)를 중앙 값을 선택할 때 가장 좋은 경우다. 따라서 \(n\)개의 원소 중 \(k\)등을 선택하는 Selection Problem로 치환된다.

결론부터 말하자면, Selection하는데 걸리는 시간때문에 Merge Sort보다 느려지게 된다. 따라서 \(n\)이 미친 듯이 크지 않는 이상 별로 의미가 없다. 그나마 가장 좋은 해결책은, \(p\)를 랜덤하게 잡는 것이다. 그러면 최소한 평균적인 기댓값이 보장되므로 최악의 경우는 피할 수 있다.

Selection Problem

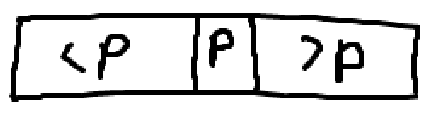
배열을 퀵소트와 똑같이 나눈다. 이 과정에서 \(O(n)\) 시간을 사용한다. \(k\)등이 \(<p\) 위치에 있으면 왼쪽을 재귀로 탐색하고, \(k\)등이 \(>p\) 위치에 있으면 오른쪽을 재귀로 탐색한다. 운이 좋으면 \(O(n)\)에 탐색 가능하지만, 운이 나쁘면 퀵소트와 똑같이 \(O(n^2)\) 시간이 걸리게 된다..

The Approximate Median Solution

딱 중간을 찾는것 보다, 타협해서 30% ~ 70% 안에 있는 값을 적당한 중앙값이라고 치고, 이 범위 안의 Pivot을 선택하는거로 하자.

1. 입력을 5개씩 끊는다.
2. 5개를 Sorting한다고 가정한다. \(\displaystyle \frac{n}{5} O(5) = O(n)\)
3. 5개 단위의 값을 3등 기준으로 Sorting한다고 가정한다.

\(\therefore\) 가운데 블럭의 3등 값이 바로 Approximate Median 값이다.

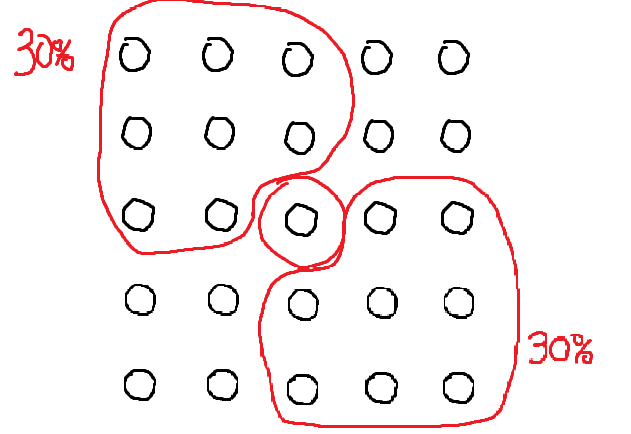
그림을 그려보면, 가운데 값보다 확실히 작은 값은 왼쪽 위 빨간색 영역이다. 가운데 값보다 확실히 큰 값은 오른쪽 아래 빨간색 영역이다. 나머지 부분은 클지 작을지 판단할 수 없는 부분.

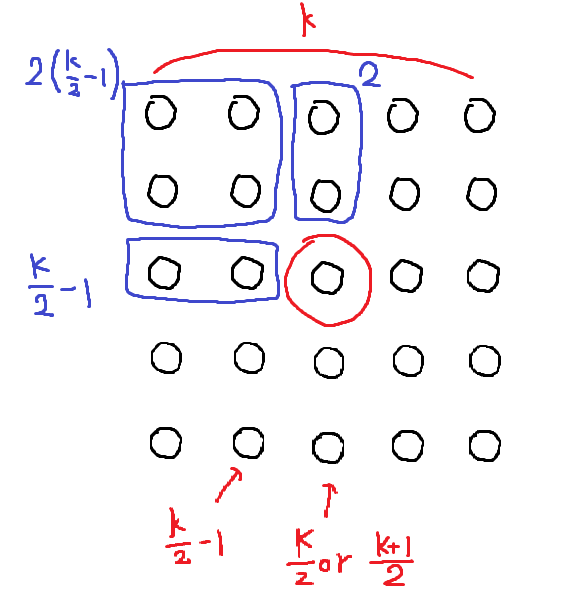
5개 단위의 블럭 개수를 \(k\)라고 할 때 \(n=5k+\alpha\)와 같다. 가운데 값은 \(\displaystyle \frac{k}{2}\)번째 또는 \(\displaystyle \frac{{k+1}}{2}\)번째에 위치한다. 가운데 영역보다 확실히 작은 원소들의 비율을 구해보자. 계산할 때 \(\alpha\)는 어차피 \(\pm 4\)의 상수 오차이므로, 고려하지 않겠다.

1. 가운데가 \(\displaystyle \frac{k}{2}\)번 째 \(\displaystyle \frac{{\frac{k}{2}-1 + 2 + 2\left( \frac{k}{2}-1 \right)}}{5k} = \frac{{ \frac{k}{2} + 1 + k -2 }}{5k}= \frac{{\frac{3}{2}k - 1}}{5k} = \frac{3}{10} - \frac{1}{5k} \simeq \frac{3}{10}\)

2. 가운데가 \(\frac{k+1}{2}\)번 째 \(\displaystyle \frac{{ \frac{k+1}{2}-1 + 2 + 2\left( \frac{{k+1}}{2} -1 \right) }}{5k} = \frac{{ \frac{k}{2} + \frac{1}{2} + 1 + k + 1 - 2 }}{5k}= \frac{{\frac{3}{2k} + \frac{1}{2}}}{5k} = \frac{3}{10} + \frac{1}{10k} \simeq \frac{3}{10}\)

즉, 가운데 값보다 확실히 작은 원소의 비율은 대략 \((30 \pm \beta)\%\)이다. 똑같이 계산하면, 가운데 값보다 확실히 큰 원소의 비율 대략 \((30 \pm \gamma)\%\) 정도이다. 따라서 가운데 값은 확실한 Approximate Median 값이다.

The Approximate Median Strategy를 사용하여 최종적으로 Selection Problem를 \(O(n)\)안에 해결해보자. \(p\)를 The Approximate Median을 선택한다. 이후 배열을 분할하고, 재귀적으로 왼쪽 파트 Selection, 오른쪽 파트 Selection하면 된다.

The Approximate Median를 고르는 시간 복잡도는 \(\displaystyle A(n) = O(n) + S\left( \frac{n}{5} \right)\)와 같다. 배열을 5개씩 끊고, 5개씩 소팅하는 과정이 \(O(n)\), 그중 가운데 블럭을 선택하는 시간이 \(\displaystyle S\left( \frac{n}{5} \right)\)이다. Selection 시간 복잡도는 \(S(n) = A(n) + O(n) + S(0.7n)\)와 같다. pivot을 Approximate Median으로 선택하기 위해 소모하는 시간이 \(A(n)\)이고고, 배열을 분할하는데 필요한 시간이 \(O(n)\)이다. \(S(0.3n)\) 또는 \(S(0.7n)\) 둘 중 하나를 선택되겠지만, 최악의 경우를 고려해 항상 \(S(0.7n)\)쪽을 선택한다고 가정하자.

\(S(n) = O(n) + S(0.2n) + O(n) + S(0.7n)\)이고, 마스터 정리에 의해 \(S(0.2n) + S(0.7n) = S(0.9n)\)로 적을 수 있다. 따라서 \(S(n)= O(n) + S(0.9n) \simeq O(n)\)이므로 Selection 문제를 \(O(n)\)에 해결했다!

Matrix multiplication

\(n \times n\) 행렬은 총 Output이 \(n^2\)칸이고, 한칸당 계산 시간이 \(O(n)\)정도이므로, \(O(n^3)\)이 걸린다. 입력 행렬이 \(n^2\)이고 출력 행렬도 \(n^2\)이므로 \(O(n^2)\)보다 빨리 만들 순 없겠다. 따라서, Lower bound가 \(O(n^2)\)이고, Upper Bound가 \(O(n^3)\)이다. 더 빠른 방법이 존재할까?

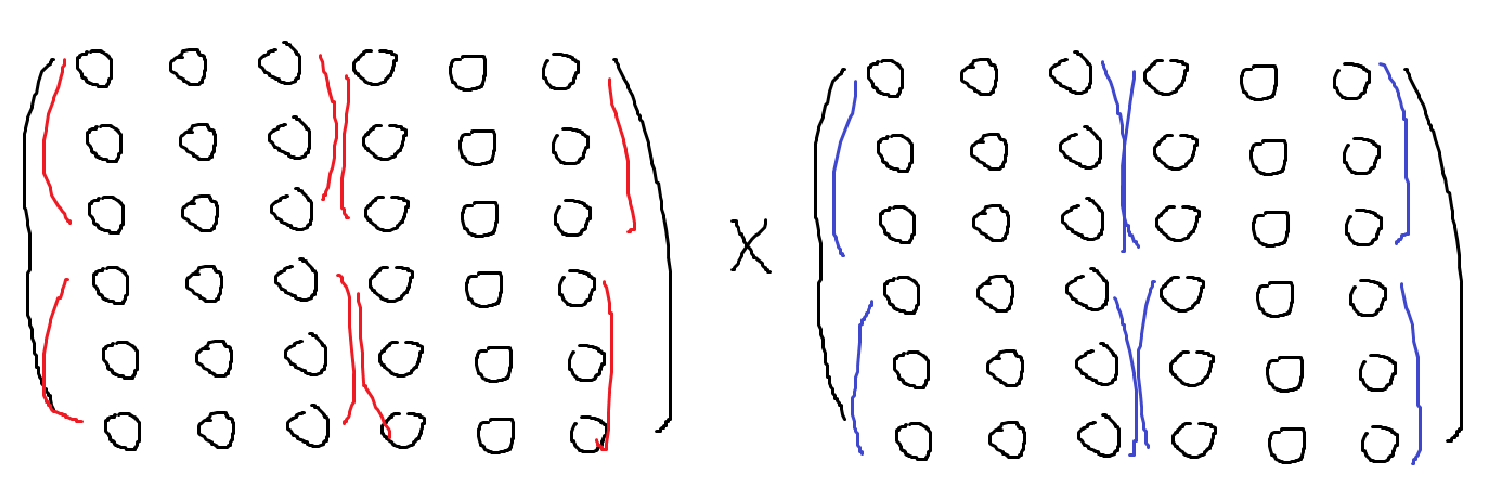
Divide and Conquer를 사용해보자. \(n\times n\) 행렬은 \(\displaystyle \frac{n}{2} \times \frac{n}{2}\) 행렬로 4조각으로 나눠서 곱을 계산하면, \(\displaystyle \frac{n}{2}\) 행렬을 총 8번 재귀 계산해야 한다. \(\displaystyle T(n) = 8T(\frac{n}{2}) \implies T(n) = O(2^{\log_{8}n}) = O(n^3)\)이다. 딱히 빨라지지 않았다.

이 문제를 푸는 Strassen’s Algorithm라는 알려진 알고리즘이 존재한다. \(\displaystyle T(n) = 7T\left( \frac{n}{2} \right) \implies O(2^{\log_{7}n}) = O( n^{2.80..})\) 이 작전은 \(n\)이 무지하게 커지면 좀 유의미하지만 메모리를 너무 많이 쓰기 때문에 별 의미가 없다. 현재는 \(O(n^{2.3})\) 시간 안에 해결하는 알고리즘이 존재한다.

Closest Pair

2차원에서 가장 가까운 정점 쌍을 찾는 방법. 각 쌍을 일일히 비교하면 \(O(n^2)\)만에 찾을 수 있긴 하다.

만약 이 문제를 1차원에서 푼다고 생각하면, 그냥 Sorting하면 된다. 이때 시간은 \(O(n\log n)\)을 사용한다. 2차원은 1차원을 포함하고 있다고 생각할 수 있다. 따라서, 2차원이 아무리 빨라봤자 1차원보다 빨라질 수 없다. 따라서 Lower Bound를 \(O(n\log n)\) 라고 예상할 수 있다.

입력 값을 나눠서, 각각 재귀적으로 답이 나왔다고 치고 두개의 답을 합칠 수 있으면 그냥 끝이다. 입력값은, 2차원 상의 좌표 배열로 주어질 것이므로 다음과 같은 전략을 사용하자.

1. x 좌표를 기준으로 Sort한다.
2. 좌우로 나눠보자.
3. 왼쪽에서 재귀적으로 답이 나왔다 치고, 오른쪽에서 재귀적으로 답이 나왔다고 치자.
4. 양쪽에서 나온 답을 합치자.

x 좌표를 기준으로 Sorting 과정은 최초 1번만 일어난다. 정렬로 \(O(n\log n)\) 시간을 사용한다.

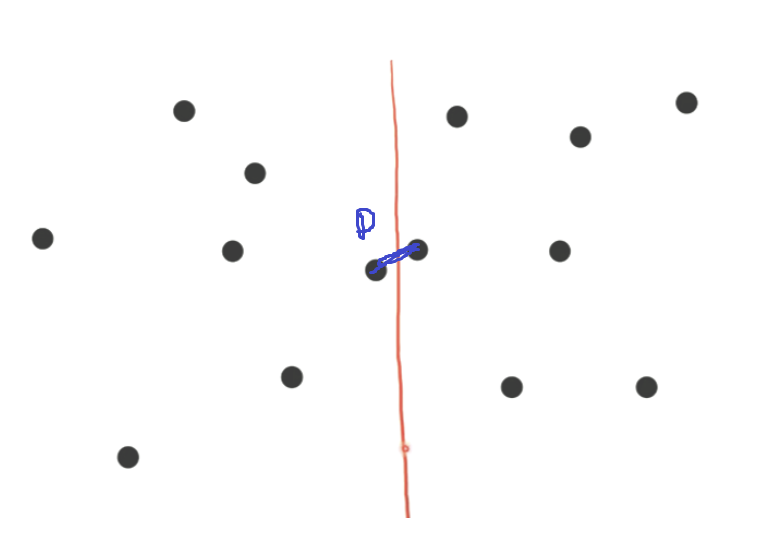
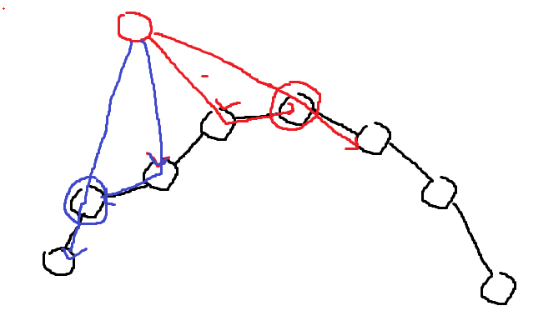
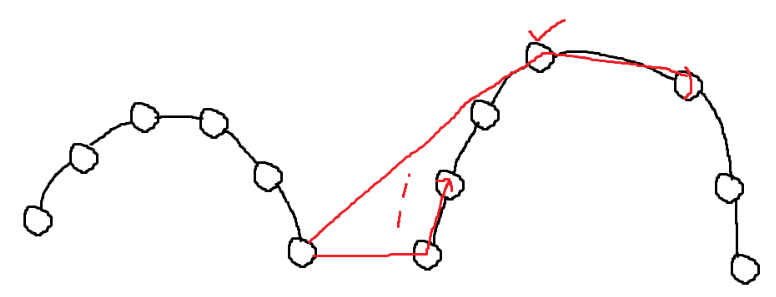
합치는 방법을 고민해야 한다. 왼쪽 답을 \(DL\), 오른쪽 답을 \(DL\)라고 하자. \(D = \text{min}(DL,DR)\)가 정답일까? 그렇지 않다.

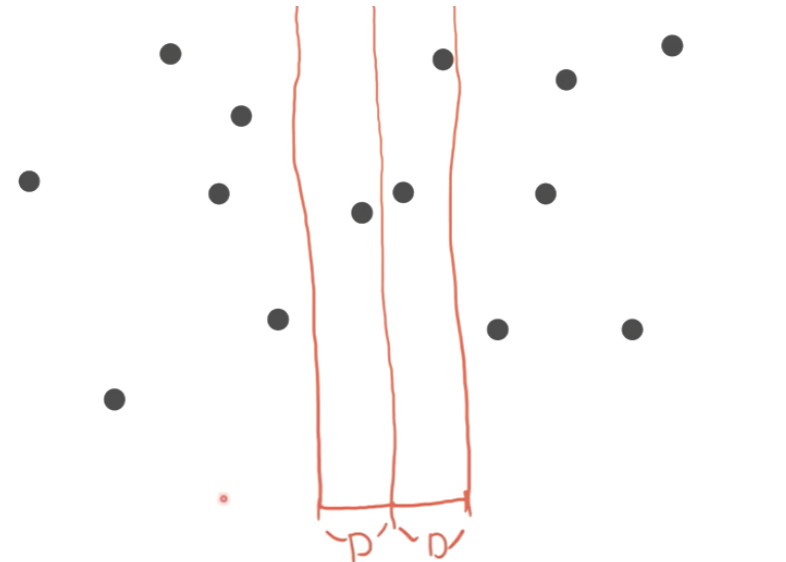
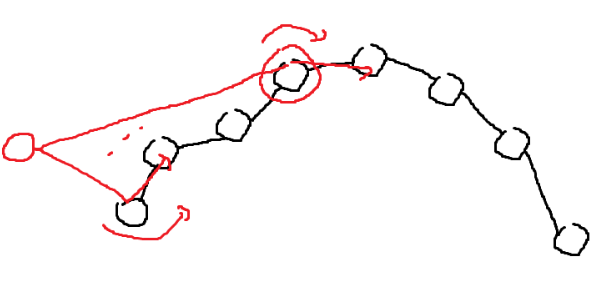
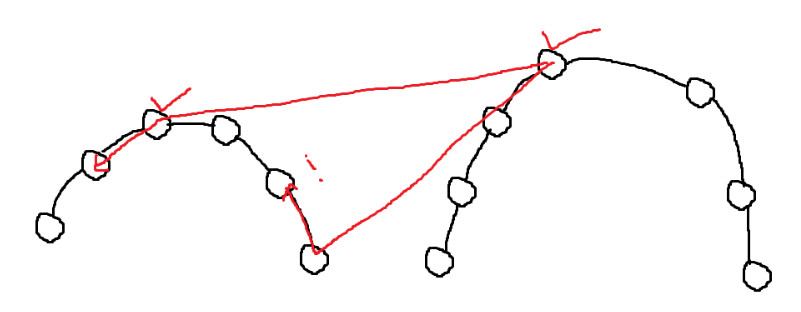
그 이유는, 위 그림과 같이 Cross된 두 점이 답이 될 수도 있기 때문이다. 그렇다면 크로스되는 좌표 사이의 거리만 체크해서 D보다 작은지 보면 될 것 같다. 일일히 전부 체크하면 최악의 경우 \(O(n^2)\)이다. 효율적으로 체크하기 위해, \(D = min(DL,DR)\)로 정의하고 중심 선으로부터 D만큼 떨어진 2개의 Band를 생각해보자.

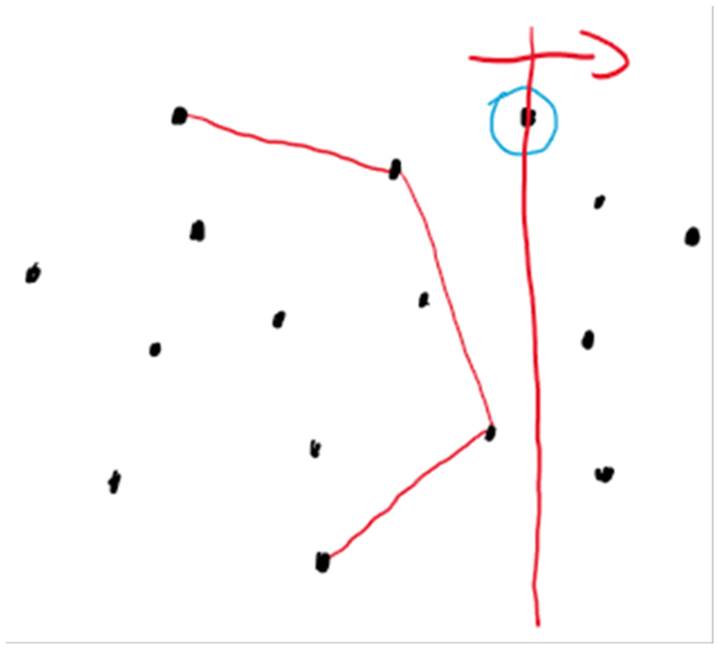
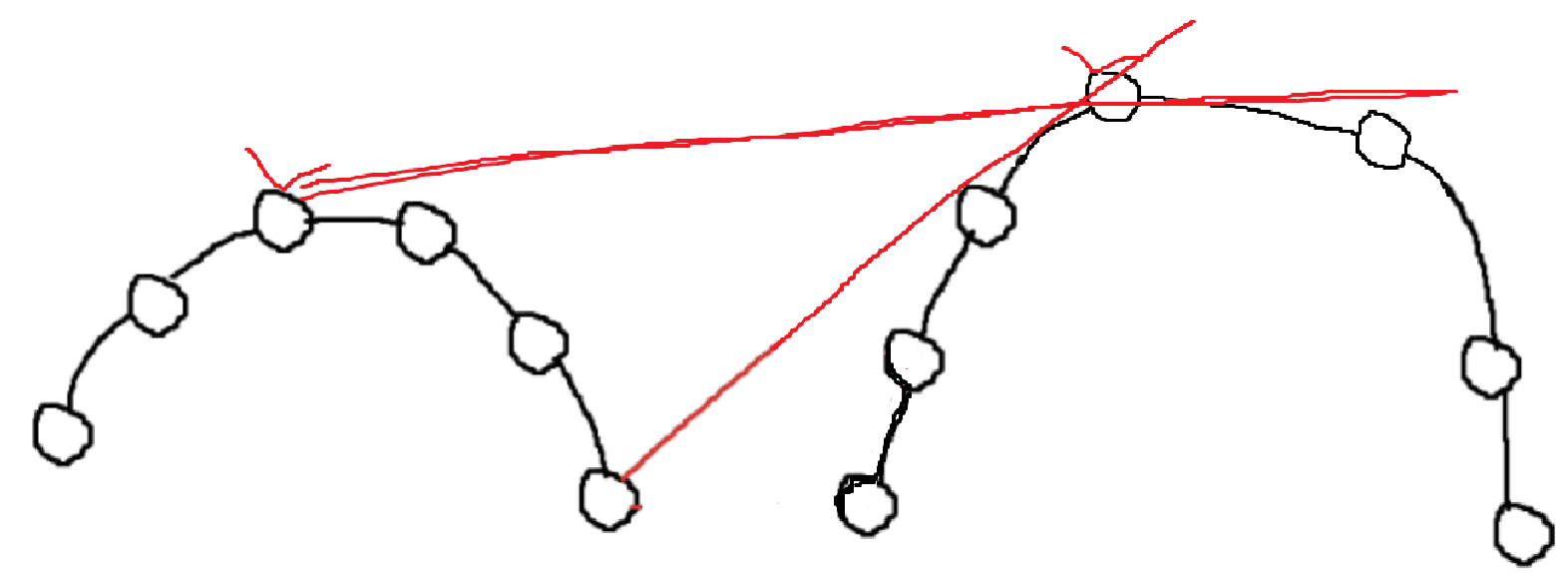
이렇게 가정하면, 선 밖에 있는 점은 반대 쪽에 있는 점보다 무조건 거리가 D보다 클 수밖에 없다. 따라서 Band 안에 있는 값만 체크하면 된다! 하지만 아직 최악의 경우 \(O(n^2)\)이다. 점들을 y축을 기준으로 정렬하고, 밴드의 맨 아래에 있는 점에서부터 시작하여 밴드 안에 있는 점 6개의 거리가 D보다 작은지 비교한다. 왜 6개만 비교하면 될까?

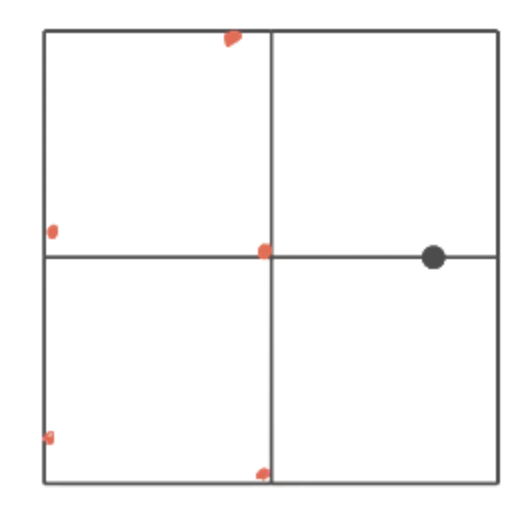
점으로부터 위 아래 D만큼 떨어지도록 가로 선을 그리면 위 그림과 같은 정사각형이 만들어진다. 이 정사각형 안에 들어올 수 있는 최대 점의 개수는 3개 뿐이다. 왜냐하면, 점 안에 있는 선 사이의 길이는 D보다 무조건 길어야 한다. D보다 더 짧았으면 애초에 그 길이가 D가 되었을 것이기 때문이다.

따라서 점 사이가 D보다 길게 둘 수 있는 점의 개수가 사각형 당 3개 뿐이다. 그리고, 사각형 밖에 있는 점과 선택한 점 사이의 길이는 D보다 무조건 길 것이므로, 비교할 필요가 없다. 또한 아래에서 위로 올라가면서 점을 체크하므로, 선택한 점 아래에 있는 점은 이미 체크가 된 점이므로 비교할 필요가 없다. 이런 이유로 선택한 점보다 위에 있는 점 6개만 비교하면 된다.

최종 시간 복잡도는 처음 x축 정렬 \(O(n\log n)\) + (y축 정렬 \(O(n\log n)\) + 검색 \(O(n)\)) \(\times\) \(\log n\) (절반씩 나뉘므로 재귀 호출이 \(\log N\)만큼 실행됨.) = \(O(n \log^2n)\)이다. 그런데, 재귀의 각 과정마다 y축에 대하여 Sorting하는거면 재귀의 결과로 나온 배열은 이미 y에 대해 Sorting되어있다. 따라서 Merge만 하면, 전체를 y좌표로 Sorting한 효과가 된다. Merge는 \(O(n)\)만에 되므로 최종 시간 복잡도는 다음과 같다. \(O(n\log n) + (O(n) + O(n)) \times \log n = O(n\log n)\)

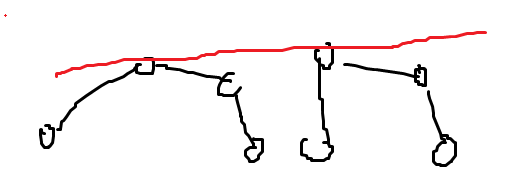
Plane Sweeping

아이디어는 Closest pair와 완전히 같다. 밴드를 오른쪽으로 조금씩 옮겨가면서 점이 빠져나간다 새로운 점은 들어오면 내 위에 3개 아래 3개 체크한다. D는 여태까지 봤던 가장 가까운 거리를 D로 잡는다. 그럼 새로운 점이 들어와서 더 작아지면 D가 점점 작아진다

Counter-Clock-Wise (CCW Algorithm)

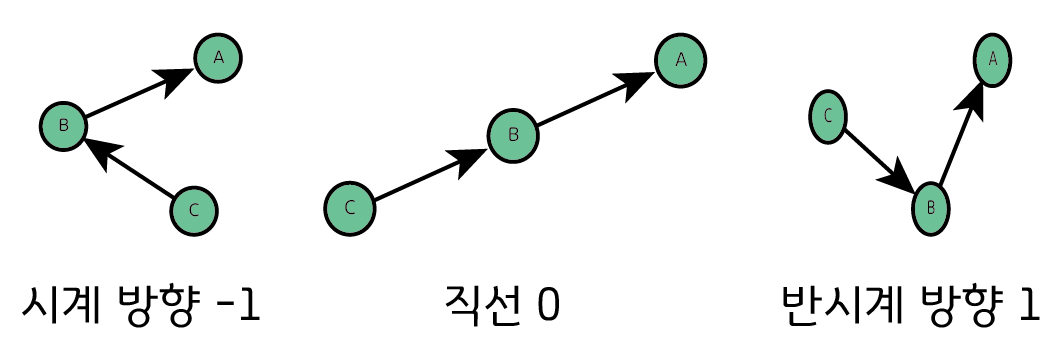
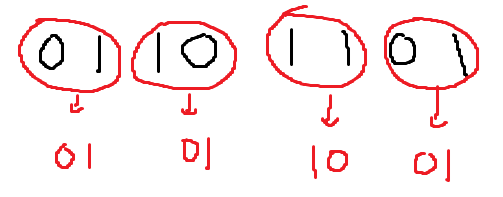
점 세개가 있을 때, 점을 이은 벡터의 회전 정보를 알려주는 알고리즘이다. 왼쪽 Case는 우회전, 가운데는 일직선, 오른쪽 Case는 좌회전이다. 회전 방향은 Curl로 결정 가능하다.

1. a, b, c 점을 순서대로 입력받고
2. a-b, b-c 벡터를 구해서
3. Curl 했을 때 음수면 우회전, 양수면 좌회전이다.

Convex Hull

Convex는 볼록, Hull은 외피 또는 덮개를 의미한다. Convex Hull은 평면 위의 모든 점을 포함하는 가장 작은 볼록 다각형이다. Convex Hull을 찾는 방법은 여러가지 알고리즘이 존재한다.

Brute Force

1. 임의의 두 점을 잡는다. \(O(n^2)\)
2. 두 점 + 나머지 모든 점들과 CCW를 해본다.
   1. 한쪽 방향만 나오면 Convex Hull 위의 점이므로, 두 점을 Hull Set에 추가한다.
   2. 다른 방향이 섞여서 나오면 컷.

\(O(n^2)\) 과정마다 n-2개 점을 고르므로, \(O(n^3)\)의 시간을 사용한다.

Package Wrapping

1. Convex Hull 위에 있다는게 보장된 가장 끝점을 잡는다. 끝점은 (min, min), (min, max), (max, min), (max, max) 4개 끝점 중 아무거나 하나를 잡으면 된다.

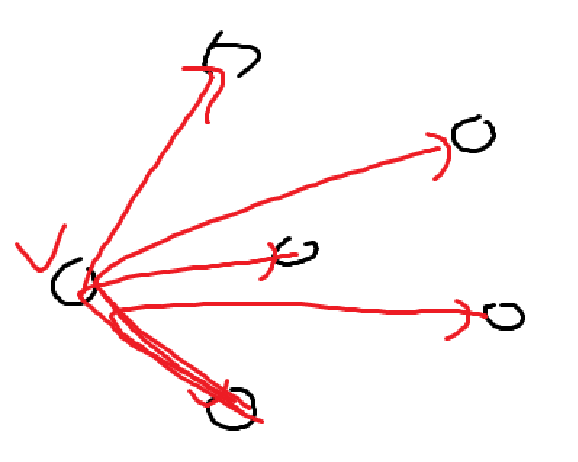
1. 이전 점, 현재 점과 모든 점에 대해 CCW를 한다. 만약 이전 점이 없다면 y좌표로 살짝 내린 임의의 점을 하나 설정하면 된다.
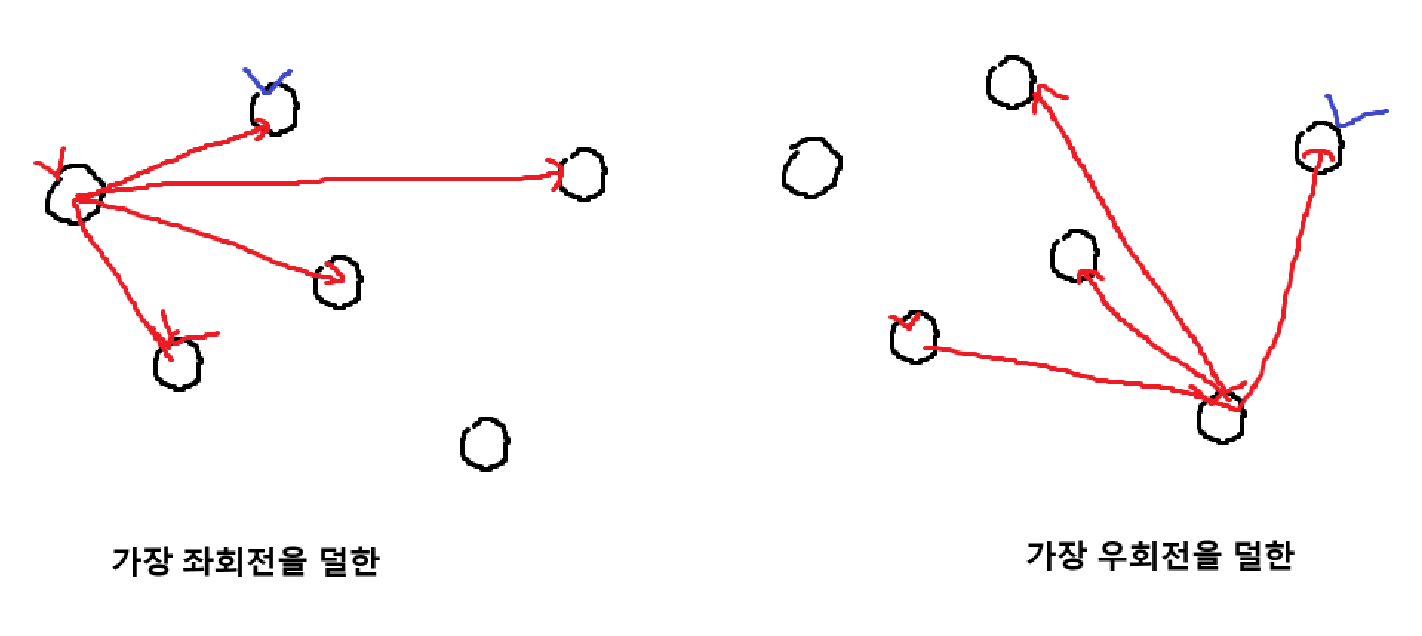
   1. 방향이 오른쪽에서 왼쪽으로 가는 경우, 가장 좌회전을 덜하는 점을 고른다.
   2. 방향이 왼쪽에서 오른쪽으로 가는 경우, 가장 우회전을 덜 하는 점을 고른다.
2. 이걸 계속 반복

n-1 점에 대해 n-1번 계산하므로 시간 복잡도는 \(O(n^2)\)이다.

Graham Scan

1. 점들의 집합 Q가 입력으로 들어온다.
2. y축이 가장 작은 점을 잡는다. \(O(n)\) 만약 y축이 같은 점이 있으면 그중 가장 x축이 작은 점을 잡는다.
3. 그 점과 다른 모든 점이 x축과 이루는 각도를 계산하여, 작은 순서대로 Sorting한다. \(O(n) + O(n\log n) = O(n\log n)\) Sorting의 비교 함수를 CCW로 넣으면 된다.
4. 각도 순서로 점을 보면서 스택에 넣다가, 우회전 할 경우 좌회전이 될때까지 스택에서 점을 제거한다.

스택에서 Push Pop은 \(O(1)\)이고, 최악의 경우여도 \(O(n)\)이므로 시간 복잡도는 \(O(n\log n)\)다. Graham Scan 알고리즘은, 입력되는 점이 변하지 않을때만 사용할 수 있다. 점이 동적으로 추가되거나 삭제되는 상황이라면, Graham Scan은 처음부터 다시 보는 수 밖에 없기 때문에 비효율적이다.

[!example]- 의사코드{title}

Stack<Vertex> GrahamScan(List<Vertex> verties)
{
    Stack<Vertex> convexHull;

    Vertex start = min_element(verties, [](Vertex a, Vertex b) {
        return a.y < b.y;
    });

    verties.remove(start);

    sort(verties, [start](Vertex a, Vertex b) {
        return CCW(start, a, b) > 0;
    });

    convexHull.push(start);
    convexHull.push(vertices.front());
    vertices.pop_front();

    for (Vertex current : vertices)
    {
        while (convexHull.size() > 1 && CCW(convexHull.second(), convexHull.top(), current) < 0)
            convexHull.pop();
            
        convexHull.push(current);
    }

    return convexHull;
}

Dynamic Case

점이 동적으로 추가되거나 삭제될 때 효율적인 알고리즘을 고려해보자. 삭제되는 경우는 빨리 풀 수 있는 방법이 없다고 알려져있다. 따라서 점이 추가되는 경우만 따져보자.

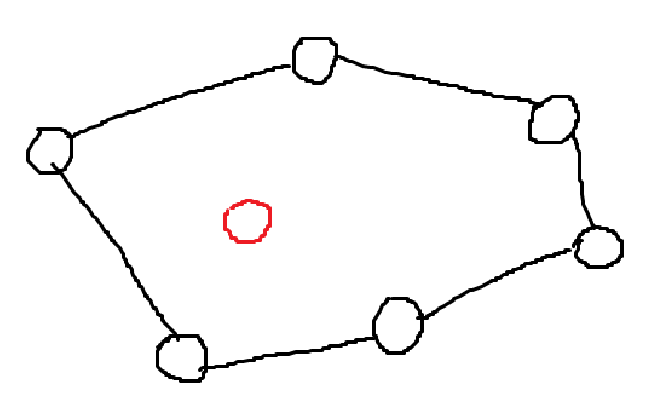
만약 점이 안쪽에 들어오면 Convex Hull이 바뀌지 않아도 된다.

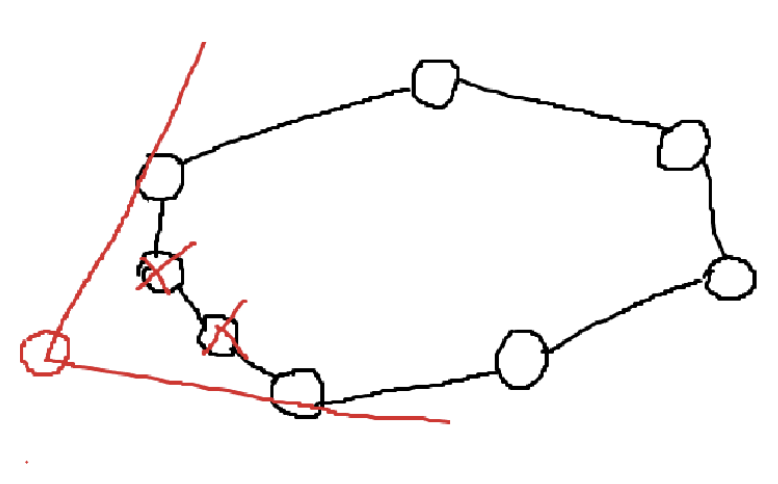
점이 밖에 들어오면 Convex Hull 모양이 바뀌어야 한다. 아이디어는, Convex Hull에 접선을 그려서, 접점과 새로운 점을 잇는다. 기존의 접점 사이에 있던 점은 다 버리면 된다.

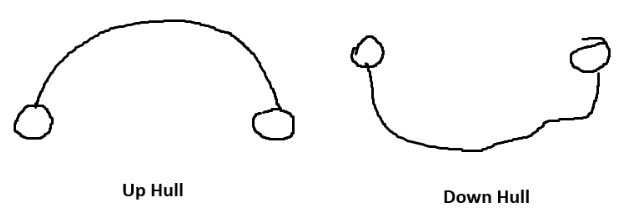
Up Hull과 Down Hull을 x 좌표가 가장 작고 큰 점을 기준으로 위 아래를 구분할 Hull이라고 정의한다. x 좌표를 기준으로 정렬된 AVL Tree를 Up Hull, Down Hull 두 개 가지고 있는 상태여야 한다.

1. 점이 안에있는지 밖에있는지 확인한다.

[!question]- 어떻게 점이 밖에있는지 안에있는지 알아?{title} CCW를 사용한다. CCW를 사용하기 위해선, 추가한 점과 나머지 두 점을 잡아야 한다. x 좌표를 기준으로 가장 인접한 Convex Hull 위의 두 점을 고르면 된다.

이후, CCW(x좌표가 작은 점 -> x좌표가 큰 점 -> 추가한 점) 를 했을 때 좌회전이면 Hull 밖의 점, 우회전이면 Hull 안의 점이라고 판단할 수 있다.

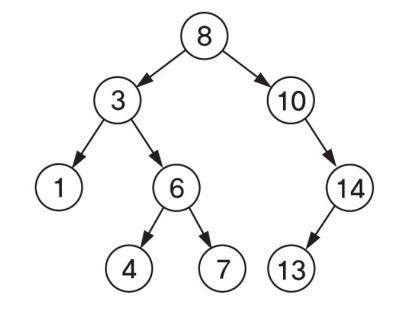
[!question]- 어떻게 AVL트리에서 가장 인접한 두개의 x 좌표를 고르는가?{title} Successor과 Predecessor를 사용하면 된다.

Successor : 어느 노드의 Key보다 크면서 가장 작은 Key를 가진 노드 Predecessor : 어느 노드의 Key보다 작으면서 가장 큰 Key를 가진 노드.

[!question]- 어떻게 Successor, Predecessor를 구하는가?{title} 먼저 Successor.

구하고자 하는 노드의 오른쪽 서브트리가 존재하면, 오른쪽 서브트리의 최소값을 구하면 된다.

\[\text{min}(\text{node}\to \text{right})\]

서브트리가 존재하지 않는다면, 부모 노드를 따라 올라가면서 최초로 부모 노드의 왼쪽 자식노드가 되는 경우를 찾는다. 그때의 부모노드가 Successor이다.

Predecessor는 정확히 대칭이다.

1. 점이 안에 있으면, 무시한다.
2. 점이 밖에 있으면,
   1. Convex Hull에 접선을 그려서 접점과 새로운 점을 잇는다.
   2. 기존의 접점 사이에 있던 점은 다 버린다.

[!question]- 접점을 어떻게 구하는가?{title}

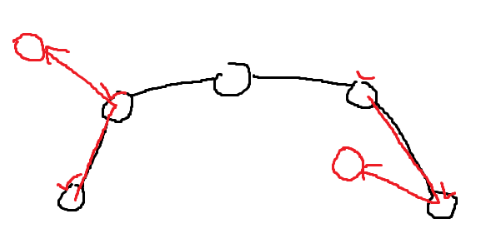
1. 접점이 두개 생기는 경우

가장 작은 x값을 가진 점의 x값을 m, 가장 큰 x값을 M이라고 하자.

\[m < x < M\]

인 경우, 접점이 두개 생긴다.

1번 과정에서 구한 x좌표를 기준으로 가장 인접한 두 점을 활용한다.

왼쪽 접접을 구할 땐, 인접한 두 점 중 왼쪽 점에서 시작하여 x좌표가 작아지는 방향으로 CCW^[Counter-Clock-Wise (CCW Algorithm)]를 진행한다.

계속 우회전(<0) 하다, 처음으로 일직선 또는 좌회전 (=0, >0)이 될 때 그 중간값이 접점이다.

만약 중간값이 끝점이라면, 끝점이 접점이다.

오른쪽 접점을 구할땐, 정확히 대칭이다. (인접한 두 점 중 오른쪽 점에서 시작하여 x좌표가 커지는 방향으로 CCW...)

1. 접점이 한개 생기는 경우

\[x < m ~~~ \mid\mid ~~~ x > M\]

인 경우, 접점이 한개 생긴다.

\(x < m\)인 경우, x좌표가 커지는 방향으로 CCW해서 처음으로 우회전하는 경우, 그 중간점이 접점이다.

\(x > M\)인 경우, x좌표가 작아지는 방향으로 CCW해서 처음으로 좌회전하는 경우, 그 중간점이 접점이다.

위 Case는 점이 Upper Hull 구간에서 추가될 때다. Lower Hull 구간에서 추가되는 경우, 위 Case의 정확히 대칭이다.

Plane Sweeping

Dynamic Case과 비슷한 원리다. 차이점은, Up Hull과 Down Hull 대신 Left Hull, Right Hull로 나누고 두개의 AVL Tree를 y 좌표값으로 정렬한다. Right Hull을 구했다고 가정하고, 딱 다음으로 오른쪽에 있는 점을 추가한다. 추가하는 방식은 Dynamic Case과 똑같다.

y축과 가장 인접한 두 점을 AVL 트리에서 찾는다. (Successor, Predecessor) 접선이 두개, 한개 그려질 수 있고, 경우를 나눠서 CCW를 사용해 접점을 찾는다. 이걸 쭉 하면 모든 점에 대한 Right Hull을 찾을 수 있다. 반대로 똑같은 과정을 한번 더 하면, Left Hull을 찾아 합치면 된다.

가운데 점 찾는데 \(O(\log n)\), 중간 점을 버리므로, 버린 점의 개수를 k라고 하면 \(O(k\log n)\)이다. 한번 버린 점은 다시 보지 않으므로, Amortization (암호테이션) 원리가 적용되어 \(k\)가 많이 계산될수록 나중에 편해진다.

이를 n번 반복하므로 \(O(n\log n)\). \(n\log n\)을 두번 반복하므로 총 시간 복잡도가 \(O(n\log n)\)이다.

Divide and Conquer

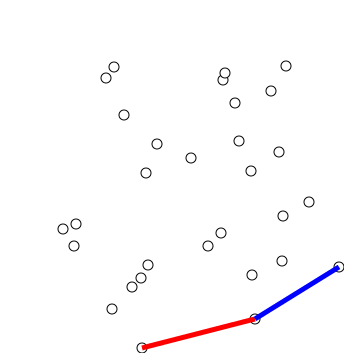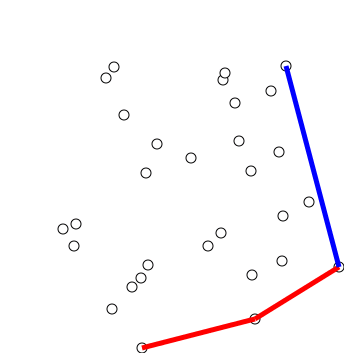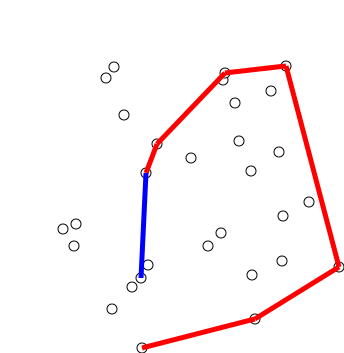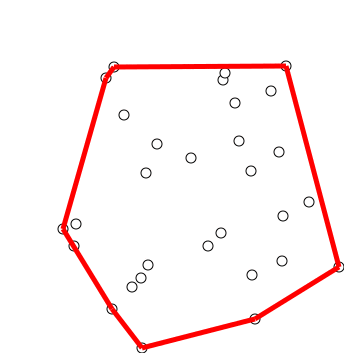
Upper Hull, Lower Hull 두개를 따로따로 구해서, 나중에 합치는 방식을 생각하자.

1. Upper Hull을 절반으로 나눠 왼쪽과 오른쪽 Upper Hull을 구했다고 치자.
2. 두 Hull의 공통 접선을 찾아서 두 접점을 연결하고, 그 중간의 점들은 싹 버린다.

[!question]- 접점을 어떻게 찾아?{title} 똑같이 CCW로 찾으면 된다.

두 Hull의 가장 왼쪽과 가장 오른쪽을 두 점으로 잡는다.

왼쪽 끝점 -> 오른쪽 끝점 -> 오른쪽 Hull에서 x가 커지는 방향 으로 CCW를 한다. (왼쪽 먼저 하던, 오른쪽 먼저 하던 상관 없음.)

계속 좌회전 하다, 처음으로 우회전했을 때 그 중간점이 접점이다.

이번엔, 접점 -> 반대쪽 Hull 끝점 -> 왼쪽 Hull에서 x가 작아지는 방향 으로 CCW를 한다.

계속 우회전 하다, 처음으로 좌회전 했을 때 그 중간점이 접점이다.

아래에서 접선을 그릴 때와 새로운 접점에서 그릴 떄 접하는 위치가 충분히 바뀔 가능성이 존재한다.

따라서, 새로운 접점 -> 반대쪽 접점 -> 오른쪽 Hull에서 x가 커지는 방향 으로 CCW를 똑같은 과정을 해야한다.

접점이 바뀌면, 또 반대쪽도 체크하고, 둘다 만족할 때까지 반복해야 한다.

while (왼쪽 조건 만족 && 오른쪽 조건 만족)
{
    while (오른쪽 CCW)
    {
        접점 위치 재설정
    }

    while (왼쪽 CCW)
    {
        접점 위치 재설정
    }
}

Karatsuba Algorithm

곱하기를 빠르게 계산하는 방법. n 자리수 \(\times\) n 자리수의 곱셈의 Upper Bound는 \(O(n^2)\)이다. 입력이 n, 출력이 n이므로 Lower Bound는 \(O(n)\)이다. \(O(n^2)\)에서 더 줄이는 방법이 있을까?

곱하는 두 수를 \(x, y\)라고 하자. 각 수를 자리수를 기준으로 앞자리를 \(x_{1} \cdot10^k\), 뒷자리를 \(x_{0}\)이라고 하자. 예를들어 숫자가 12478042이면 \(x_{1} = 1247\), \(x_{0} = 8042\), \(10^k = 10^4\)이다.

\(x_{1}10^k + x_{0} = x\), \(y_{1} 10^k +y_{0} = y\)와 같이 두개로 나누고, \(xy\)를 계산한다. \(x_{1}y_{1}10^{2k} + (x_{1}y_{0} + x_{0}y_{1})10^k + x_{0}y_{0} = xy\), 이후 \(x_{1}y_{1}\), \(x_{0}y_{0}\)은 계산하고, \(x_{1}y_{0} + x_{0}y_{1}\)는 다음 식을 응용해서 계산한다.

\((x_{1} + x_{0})(y_{1} + y_{0})= x_{1}y_{1} + (x_{1}y_{0} + x_{0}y_{1}) + x_{0}y_{0}\) \(\implies x_{1}y_{0} + x_{0}y_{1} = (x_{1} + x_{0})(y_{1} + y_{0}) - x_{1}y_{1} - x_{0}y_{0}\)

\(x_{1}y_{1}\), \(x_{0}y_{0}\) 계산 결과를 이용하면, 두번 곱셈 연산이 필요한 \(x_{1}y_{0} + x_{0}y_{1}\)을 곱셈 한번만에 계산할 수 있다. 시간 복잡도를 계산하면 \(T(n) = 3T\left( \frac{n}{2} \right) + O(n)\)이고, Master Theorem을 사용하면 \(T(n) = O(n^{\log_{2}3}) \simeq O(n^{1.6})\)이다. 이 알고리즘 때문에 컴퓨터로 나눗셈보다 곱셈을 계산하는게 훨씬 빠르다.

32비트 중 1의 개수를 빠르게 세는 방법

unsigned int가 갖는 1인 비트 개수를 빠르게 세는 방법. 예를들어 0010 1101 1101 0010 1011 1011 0011 0111 => 19개와 같다.

가장 쉽게 생각해볼 수 있는 방법은, Bit Mask를 만들어서 한칸씩 Shift하며 & 연산으로 개수를 세는 것이다. 구현한 코드는 다음과 같다.

int bit_count(unsigned int n) 
{
    int count = 0;

    while (n != 0)
    {
        count += n & 1;
        n >>= 1;  // right shift
    }

    return count;
}

---

n과 n-1을 and하면, 가장 오른쪽에 있는 1비트가 하나씩 사라진다. 반복 횟수 = Count 횟수임을 이용한다. 정말 n과 n-1을 and하면 사라지는가?

\(00101101 ~\&~ (00101100) = 00101100\) \(00101100 ~\&~ (00101011) = 00101000\) \(00101000 ~\&~ (00100111) = 00100000\) \(00100000 ~\&~ (00011111) = 00000000\)

최악의 경우, \(O(32)\)이다. 구현 코드는 다음과 같다.

int bit_count2(unsigned int n) 
{
    int count = 0;

    while (n != 0)
    {
        count++;
        n = n & (n-1);
    }

    return count;
}

---

가장 빠른 방법

int popcount(unsigned int n)
{
    n = (n >>  1 & 0x55555555) + (n & 0x55555555);
    n = (n >>  2 & 0x33333333) + (n & 0x33333333);
    n = (n >>  4 & 0x0F0F0F0F) + (n & 0x0F0F0F0F);
    n = (n >>  8 & 0x00FF00FF) + (n & 0x00FF00FF);
    n = (n >> 16 & 0x0000FFFF) + (n & 0x0000FFFF);
    
    return n;
}

이건 무슨 코드냐? 16진수들의 각 2진수 값은 다음과 같다.

\(0\text{x}55555555 = 0101~0101~0101~0101~0101~0101~0101~0101\) \(0\text{x}33333333 = 0011~0011~0011~0011~0011~0011~0011~0011\) \(0\text{x}\text{0F0F0F0F} = 0000~1111~0000~1111~0000~1111~0000~1111~\) \(0\text{x00FF00FF} = 0000~0000~1111~1111~ 0000~0000~1111~1111\) \(0\text{x0000FFFF} = 0000~0000~0000~0000~1111~1111~1111~1111\)

1. 0110 1101 » 1 = 0011 0110
2. 0011 0110 & 0x55555555 = 0001 0100
3. 0110 1101 & 0x55555555 = 0100 0101
4. 0001 0100 + 0100 0101 = 01 01 10 01

이는 1칸씩 짝지어서, 더하는 것과 같다.

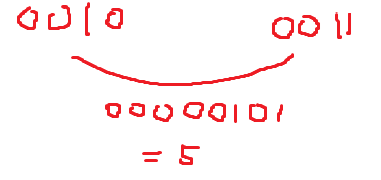
그다음은, 2칸씩 짝지어서 더한다.

그다음은, 4칸씩 짝지어서 더한다.

위 예시는 총 비트가 8개이므로 여기까지 해도 답이 구해진다. 32비트면, 8칸씩, 16칸씩 짝지어서 총 32비트까지 연산해야된다. 갈수록 안쓰는 0 공간이 많아지는걸 이용하여 최적화할 수 있다. 실제로 사용되는 코드는 아래 최적화된 코드이다. 시간 복잡도는 \(O(5)\)이다.

int popcount(unsigned int n)
{
    n = n - ((n >> 1) & 0x55555555);
    n = (n & 0x33333333) + ((n >> 2) & 0x33333333);
    n = (n + (n >> 4)) & 0x0F0F0F0F;
    n = n + (n >> 8);
    n = n + (n >> 16);

    return n & 0x3F;
}