알고리즘 2. Greedy Algorithm

게시 2024/12/28 업데이트 2025/01/13

By 신희곤

37 분읽는 시간

건국대학교 알고리즘 김성열 교수님의 수업을 정리한 내용입니다.

Greedy

모든 경우를 다 따져보지 않아도 현재 상태에서 최선이라고 생각되는 경우만 선택했을 때 답이 구해지는 알고리즘이다. 최선의 기준은 여러가지가 있을 수 있고, 기준에 따라 그리디 알고리즘이 해를 찾을 수도, 못찾을 수도 있다. 따라서 최선을 선택하는 방법을 잘 선택하는 것이 핵심이다.

예를들어, MST를 찾는 Kruskal Algorithm은 대표적인 그리디 알고리즘이다. 과정은 다음과 같다.

최소 간선을 찾는다.
그 간선을 연결했을 때, Cycle이 생기지 않으면 추가하고, 생기면 스킵한다.
간선개수가 n-1 될때까지 반복한다.

Greedy가 최적해를 찾을 수 있는지 증명하는 방법

증명의 출발점은, 답은 하나가 아닌 여러개일 수 있다는 것에서 출발한다. Step은 다음과 같다.

이미 답인게 밝혀진 답이 있다고 가정한다.
알고리즘대로 따라서 가다가, 답과 다른 결과가 나왔을 때 그 결과도 답이 될 수 있다는 것을 보인다.
선택지가 답을 내는 선택지밖에 없기 때문에 그리디 알고리즘이 최적해를 낸다는 것을 증명한다.

Prim Algorithm

MST를 찾는 그리디 알고리즘. 과정은 다음과 같다.

아무 노드에서부터 시작한다.
인접한 Edge들 중 가장 작은 Weight를 가지면서 싸이클을 만들지 않는 간선을 추가한다.
Spanning Tree가 될 때까지 반복

\(n\)을 노드 개수, \(m\)을 노드 개수라고 하면 시간 복잡도는 \(O(n+m\log m)\)과 같다. 그 이유는 각 엣지마다 Heap 연산 \(\log m\)을 수행하고, 모든 노드마다 방복하지만 암호테이션에 의해 한 노드에서 많은 작업을 수행하면 다른 노드에서 적게 수행한다. 총 N번 수행되므로 N이 더해진다.

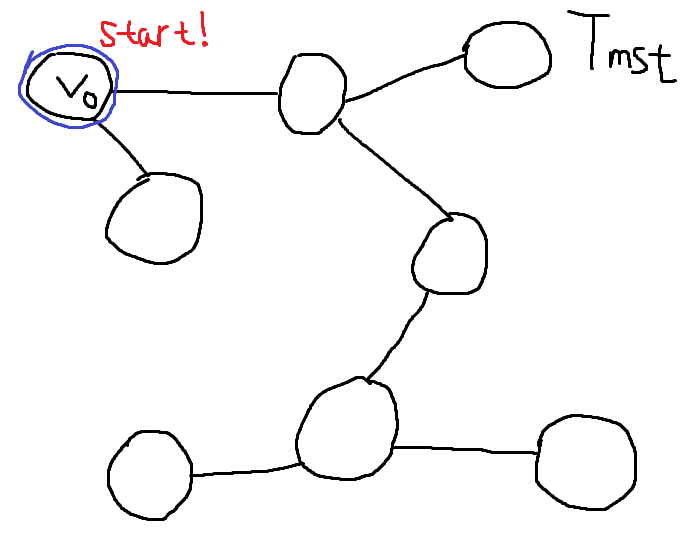
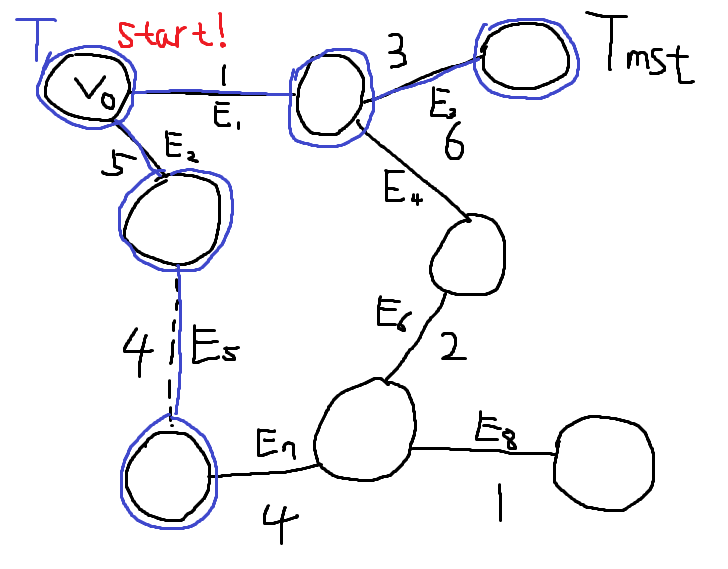
[!tip]- 정확성 증명{title} 목표는, 복잡한 그래프에서 올바른 Minimum Spanning Tree를 추출하는 것이다. 정답이라고 이미 밝혀진 Minimum Spanning Tree를 \(T_{mst}\)라고 가정하자. Prim Algorithm을 이용해서 내가 만들고있는 Minimum Spanning Tree를 \(T\)라고 가정하자. \(T\)와 \(T_{mst}\)는 Edge Set이다.
\(V_{0}\) 노드에서 시작하자. 아무 노드에서 시작해도 된다.
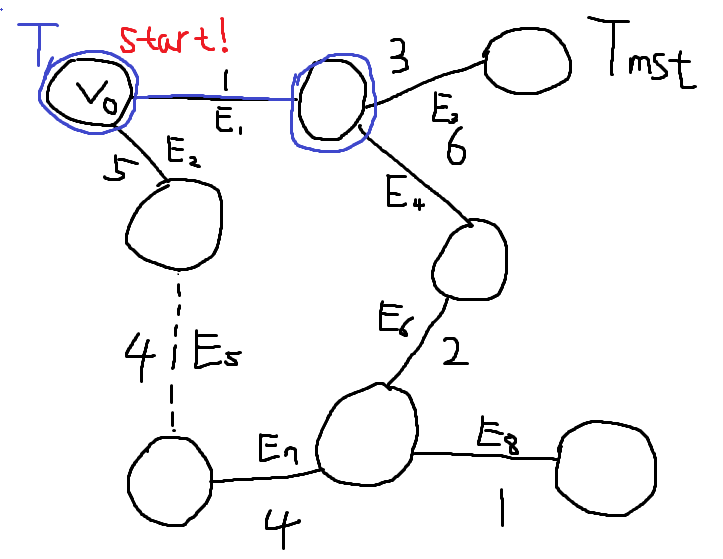
처음엔 두 엣지 \(E_{1}, E_{2}\)중 하나를 고를 수 있다. \(E_{1}\)가 가장 Weight가 작고, 싸이클을 만들지 않으므로 \(T\)에 \(E_{1}\)을 추가한다. \(T = \{E_{1}\}\)
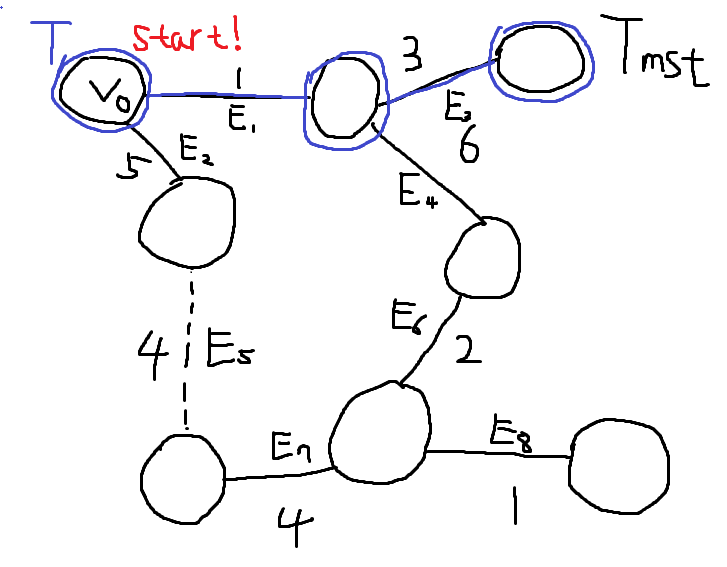
\(E_{2}, E_{3}, E_{4}\)중 하나를 골라야 한다. \(E_{3}\)이 가장 작고, 싸이클을 만들지 않으므로 \(E_{3}\) 엣지를 \(T\)에 추가한다. \(T = \{E_{1}, E_{3}\}\)
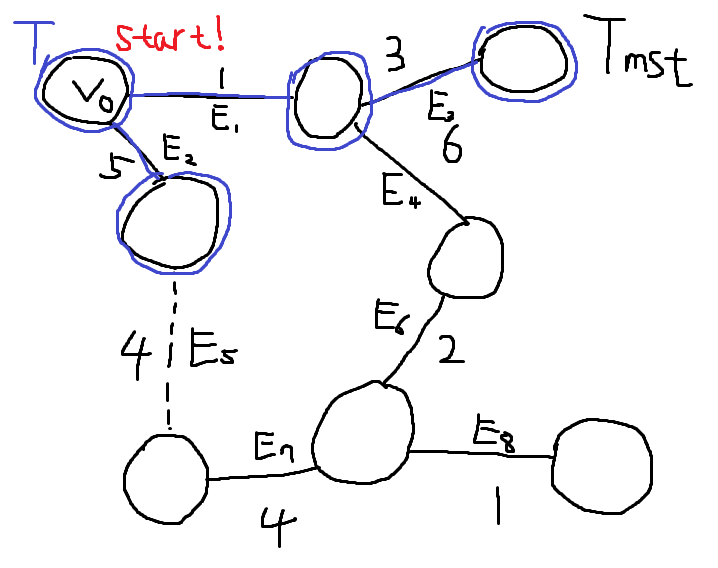
\(E_{2}, E_{4}\) 중 \(E_{2}\) 엣지가 가장 Weigt가 작고, 싸이클을 만들지 않으므로 \(E_{2}\) 엣지를 \(T\)에 추가한다. \(T = \{ E_{1}, E_{3}, E_{2} \}\)
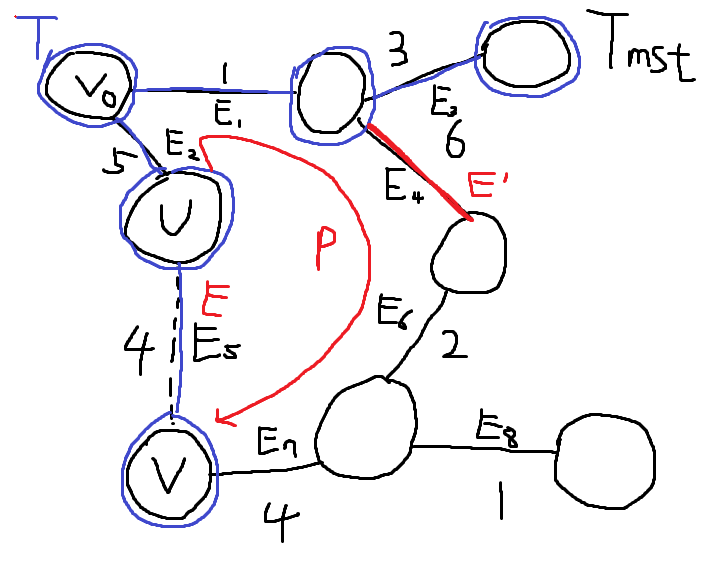
\(E_{4}, E_{5}\) 중 \(E_{5}\) 엣지가 웨이트가 가장 작고, \(T\) 기준으로 싸이클을 만들지 않으므로 \(E_{5}\) 엣지를 \(T\)에 추가한다. \(T = \{ E_{1}, E_{3}, E_{2}, E_{5} \}\) 여기서 문제가 발생한다. \(T_{mst}\) 기준으로 \(E_{5}\)를 추가하게 되면 싸이클이 발생한다.
\(T_{mst}\)에서 정점 U에서 정점 V로 가는 경로는, 트리의 성질에 의해 P 하나 뿐이다. \(T\)의 다음 선택 고려 대상이자, 아직 포함되지는 않고 P 경로에 포함된 엣지 \(E'\)는 반드시 하나 존재한다. 우리는 Prim Algorithm을 잘 지키면서 왔으므로 문제의 엣지 \(E\)와 \(E'\)의 Weight는 \(E\)가 작거나 같다. \(w(E) \leq w(E')\) 따라서, 기존에 알고있던 답 \(T_{mst}\)에서 \(E'\)를 빼버리고, \(E\)를 추가한 새로운 Tree를 \(T_{new}\)라고 하자. \(T_{new} = T_{mst} - \{ E' \} + \{ E \}\) Tree Edges의 총 Weight의 합은 \(T_{new}\)가 \(T_{mst}\)보다 반드시 작거나 같다. \(w(T_{new}) \leq w(T_{mst})\) 따라서 \(T_{new}\)는 새로운 MST가 된다.
이 과정은 Prim 알고리즘이 선택한 모든 간선에 대해 적용할 수 있다. 각 단계에서, 만약 선택된 간선이 \(T_{mst}\)에 없다면, 위의 교환 과정을 통해 \(T_{mst}\)를 수정하여 새로운 MST를 만들 수 있다. 결과적으로, Prim 알고리즘이 선택한 간선들을 포함하는 MST가 존재한다.

[!tip]- 구현{title} 입력은 그래프를 받는다. \((V, E)\)
1 2 Set T; Set U = { V_0 };
Edge Set T와, Node Set U를 만든다. 이후, \(V_{0}\)의 인접한 노드를 Priority Queue (우선순위 큐)에 추가한다.
1 2 3 4 5 6 7 8 9 10 11 12 while (U != V) { // 우선순위 큐에서 엣지 하나를 뽑는다. // 만약 엣지 양쪽에 연결된 노드가 모두 U에 들어있다면, // 싸이클이 생긴다는 뜻. => Continue // 아니라면, // U에 들어있지 않는 노드를 U에 추가하고, // 인접한 Edge를 우선순위 큐에 추가한다. // 뽑은 Edge를 T에 추가한다. } return (U, T);
인접한 노드를 바로바로 꺼낼 수 있게, 그래프를 구현할 때 노드 -> 인접한 엣지 Set 을 갖는 Map을 하나 갖고있어야 한다. 인접 리스트

Kruskal Algorithm

MST를 찾는 그리디 알고리즘. 과정은 다음과 같다.

모든 엣지 중 최소 간선을 찾는다.
간선을 추가했을 때, Cycle이 생기지 않으면 추가한다.
간선개수가 n-1 될때까지 반복한다.

Edge Sorting하는데 \(m\log m\)이 걸리고, Union find에서 걸리는 시간이 상수 시간이므로 시간 복잡도는 약 \(O(m\log m)\)와 같다. 더 정확히는 \(O(M\log M+M\alpha(N))\)이고, \(\alpha(N)\)은 간선 하나를 cycle 여부 판단하는데 걸리는 시간이다. 이는 굉장히 작은 값이다.

정답이라고 이미 밝혀진 MST를 \(T_{mst}\)라고 가정하자. Kruskal Algorithm을 이용해서 내가 만들고있는 MST를 \(T\)라고 가정하자. \(T\)와 \(T_{mst}\)는 Edge Set이다. Kruskal Algorithm을 사용해서 엣지를 추가하는 중 \(T_{mst}\)에 없는 Edge를 \(e\)라고 하자. \(e\)를 \(T_{mst}\)에 추가하면 싸이클이 생길텐데, 이 싸이클에 있는 엣지 중 \(T\)에 없는 임의의 Edge를 \(e'\)라고 하자.

만약 \(w(e) > w(e')\)면, \(e\)가 아니라 \(e'\)를 넣었을 것이므로 알고리즘과 모순이다. \(w(e) = w(e')\)면, \(T_{mst}\)에서 \(e'\)를 빼고 \(e\)를 넣은 Tree는 새로운 정답이 된다. \(w(e) < w(e')\)면, \(T_{mst}\)는 답이 아니므로 가정과 모순이다.

따라서, 모순이거나 새로운 답을 찾거나 원래 답을 찾거나 셋중 하나의 경우밖에 없기 때문에, Kruskal Algorithm은 항상 MST를 찾는다.

[!tip]- Kruskal은 모든 가능한 답을 찾을 수 있을까?{title} \(w(e) < w(e')\)이거나 \(w(e) > w(e')\)인 경우는 모순이므로 고려하지 않아도 된다. 새로운 답이 생기는 경우는, \(w(e) = w(e')\)인 \(e'\)가 존재하는 경우 뿐이다.
만약 알고리즘을 구현하는 단계에서, \(e\)가 아니라 \(e'\)를 먼저 선택했다면 그냥 \(T_{mst}\)를 찾게 된다. \(T_{mst}\)는 정답이라고 가정했던 것이므로, \(T_{mst}\)가 어떤 정답이던지 Kruskal이 다 찾아낼 수 있다.

[!tip]- 모든 Weight가 다른 Graph의 MST는 한개밖에 없을까?{title} 만약 모든 Weight가 다르면, 위 증명에서 \(e'\)를 선택할 수 있는 선택권이 없다는 것과 같다.
따라서 알고리즘을 쭉 돌리면, Kruskal은 1개의 답밖에 찾을 수 없다.
Kruskal은 이미 모든 답을 찾을 수 있다는 것을 증명했으므로 모든 Weight가 다른 Graph의 MST는 단 한개만 존재한다.

[!example]- 구현{title} 최소 간선은 Edge를 Weight 순서로 Sorting하면 쉽게 찾을 수 있다. Cycle이 존재하는지 판단하는 방법은 Union-Find Sets (Disjoint Sets)을 사용하면 된다. Union/Find Set의 Find 연산으로 양쪽의 노드가 같은지 검사해서 같으면 Edge를 추가하지 않고 같지 않으면 Edge를 추가한다. Edge를 추가하는 것을, 두 노드 집합을 합집합하는 Union 연산과 동일하게 생각할 수 있다.

  
Graph getMinimumSpanningTree(Graph graph)
{
    Graph minimunSpanningTree;
    DisjointsSet<V> sets;
    Verties verties = grpah.getVerties();
    Edges edges = graph.getEdges();
   
    minimunSpanningTree.addVerties(verties);
    sort(edges, weight);
    
    int vertexSize = verties.size();
    int edgeSize = 0;
    for (Edge edge : edges) {
        if (edgeSize == vertexSize) break;
        
        Vertex leftRoot = sets.find(edge.leftNode);
        Vertex rightRoot = sets.find(edge.rightNode);
        int weight = edge.weight;
        if (leftRoot != rightRoot) {
            minimunSpanningTree.addEdge(edge);
            sets.union(leftRoot, rightRoot);
            edgeSize++;
        }
    }
    
    return minimunSpanningTree;
}

Dijkstra Algorithm

Directed or Undirected Graph에서, A Node 노드로부터 다른 모든 노드에 대한 Shortest Path를 찾는 방법. 그래프와 시작 노드를 넣으면 시작 노드로부터 다른 모든 노드까지의 최단 경로를 반환해야 한다. 만약 가중치가 음수를 가지면 사용할 수 없다.

기본 아이디어는 \(S\to B\)로 가는 Shortest Path가 \(S\to C \to A \to B\) 이면, \(S\to A\)로 가는 경로도 Shorest Path라는 것을 이용한다. 왜냐하면, \(S\to A\)로 가는 경로가 더 짧은 길이 있다면, \(S\to B\)로 가는 경로도 더 줄일 수 있기 때문이다. 이는 필요 충분 조건이기 때문에, A와 B 사이의 길이 모두 Shorest Path이면 \(A\to B\)로 가는 길 또한 Shorest Path이다.

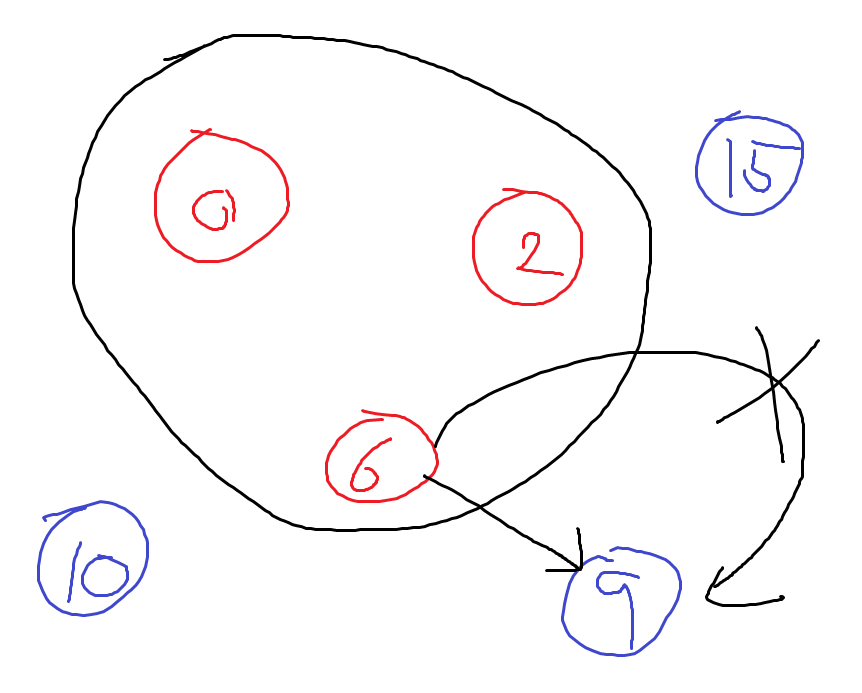
두개의 집합을 정의한다. Red Sets은 정답(Shortest Path)을 아는 노드, Blue Sets = Red Sets Node만 거쳐서 갈 수 있는 노드라고 하자. Blue Sets의 Node에는 Red Sets Node만 거쳐서 갈 수 있는 Shortest Path’s Length (최단거리)가 적혀있다. 이를 Path Weight라고 하자.

처음에는 Source Node만 Red Sets이다. Blue Sets는 Red Sets의 Node만 거쳐서 갈 수 있는 Nodes인데, Source Node밖에 없으므로 Source Node로부터 인접한 노드가 모두 Blue Sets에 들어간다.
Blue Sets가 Empty 될 때까지 그리디를 돌린다.

시작 노드에서 출발하여 나머지 Red Nodes를 거쳐서 갈 수 있는 가장 짧은 Path를 가진 Blue Node는 Shortest Path를 찾은 것과도 같다. 귀류법으로 쉽게 증명 가능. 따라서, Min Path Weight를 갖는 Blue Node를 뽑아 Red Set로 옮긴다. …(1) 그리고 그 노드와 인접한 Node의 Path Weight값을 업데이트한다. 만약 인접한 Node가 Blue Node라면 현재 Red Set로 옮겨진 Node의 Path Weight + Direct Edge Weight < Adject Path Weigth 일 때 Path Weight 값을 업데이트한다. …(2) 만약 인접한 노드가 아무것도 아니라면 Blue Set에 (Path Weight + Direct Edge Weight, Adject Node)를 추가한다.

[!question]- (1) 왜 그냥 정답으로 봐도 될까?{title}
그것보다 더 최단거리로 가는 길이 있다고 가정해보자.
그러려면, 그것보다 더 짧은 엣지를 거쳐서 나와야 하는데, 그런 엣지가 있다면 애초에 그 Edge를 선택했을 것이다.
따라서 귀류법에 의해 모순이고, Blue Sets의 Weight중 가장 작은게 최단거리가 된다.

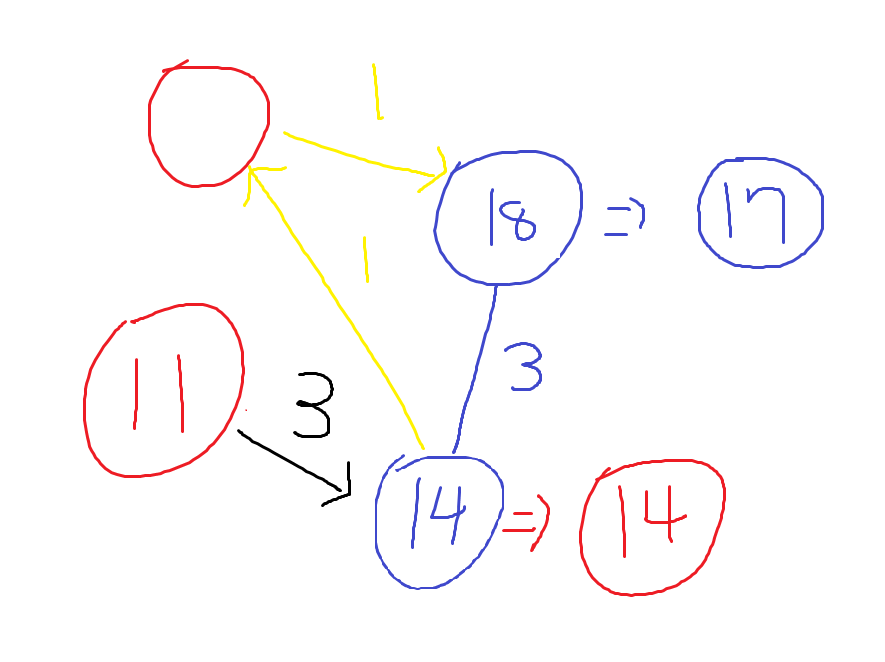
[!question]- (2) 왜 Direct Edge만 체크할까?{title}
노란색 같은 케이스는 없을까?
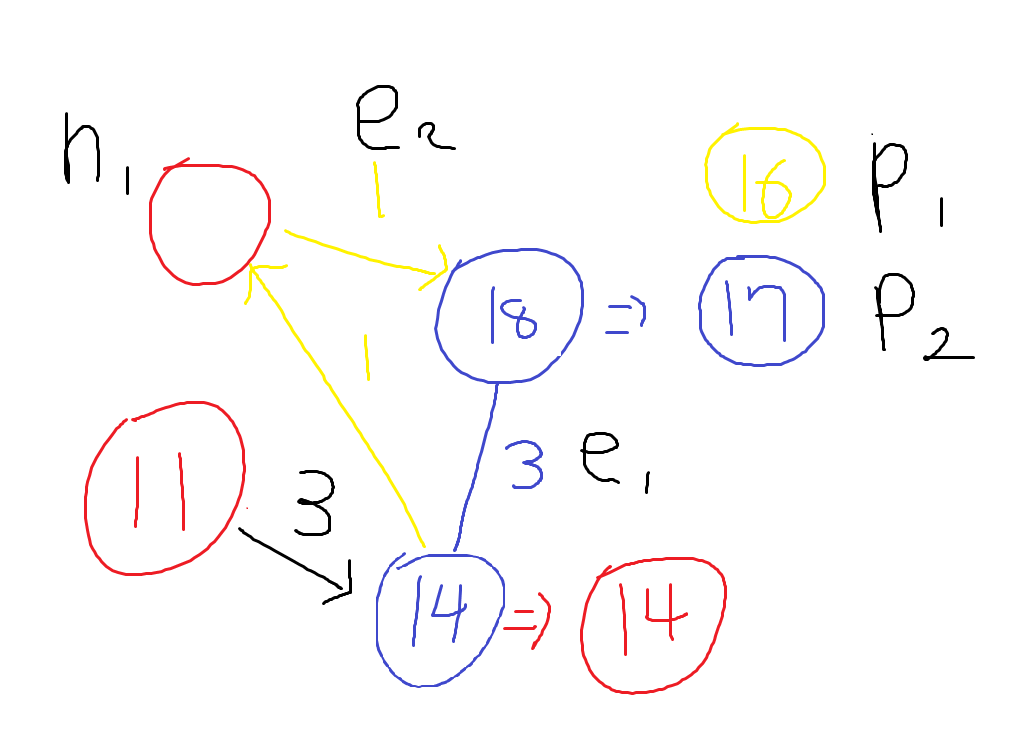
만약 노란색 케이스가 있어서, Direct Edge에서 더하는 것보다 더 작은 Shorest Path를 만든다고 가정해보자.
노란색 결과로 만들어지는 Path Weight를 \(p_{1}\), 파란색 업데이트 결과로 만들어지는 Path Weight를 \(p_{2}\)라고 하자.
\[w(n_{2}) + w(e_{1}) = p_{2}\]
만약 노란색 Edge와 같이 거쳐서 노드에 도달한다면, \(n_{1}\) to 목적지 노드로 가는 \(e_{2}\)와 같은 Edge가 반드시 하나 존재한다.
최소한
\[w(n_{1}) + w(e_{2}) < p_{2}\]
는 반드시 만족되어야 노란색 Path가 존재할 가능성이 있다.
하지만 저 조건이 만족이 되면, blue 노드로 가는 Path Weight가 정의에 의해 기존보다 더 작은 값이 되었어야 한다.
따라서 모순이고, Direct가 아닌 다른 곳을 거쳐서 가는 Edge는 생각하지 않아도 된다.

\(n\)을 node 수, \(m\)을 edge 수라고 하자. 만약 우선 순위 큐의 describe key 연산으로 구현하는 방식을 사용하면 \(O((n+m)\log n)\)이다. 일단 push하고, 나머지 중복 값은 무시하는 식으로 구현하면 \(O((n+m)\log m)\)이다. 후자의 방법이 구현이 압도적으로 쉽다. describe key 연산이 상수배만큼 시간이 더 걸리기 때문에 둘의 시간 차이가 크게 나지 않는다.

[!tip]- 구현{title} 기본적인 다익스트라 구현은 Shortest Path의 길이를 찾는다. 살짝만 바꾸면 하나의 Path를 찾을 수 있게 만들 수 있고, 거기서 또 살짝만 바꾸면 모든 Path를 찾을 수 있다.

Blue sets 중에 가장 Path값이 작은걸 계속 뽑아야 하기 때문에, Priority Queue (우선순위 큐)가 사용된다. Blue sets를 key = Node, priority = maybeShortestDistance 를 갖는 priority queue로 구현할 수 있다. 의사 코드는 다음과 같다.

// 시작 노드로부터 다른 모든노드로 가는 최단 weight를 구하는 알고리즘
map<Node, ShortestDistance> redSet
PriorityQueue<Node> blueSet

redSet에 { startNode, 0 }을 넣는다.
blueSet에 startNode와 연결된 노드를 넣는다.

blueSet가 빌 때까지 반복
    우선순위 큐인 blueSet에서 원소를 pop.
    pop한 원소가 redSet에 있다면
        continue.
        
    그 원소와 ShortestDistance 값를 redSet에 넣는다.
    (ShortestDistance 값은 PQ의 weight + edge weight로 구함)
    
    pop한 원소와 연결되어 있는 노드들 중에
        이미 redSet에 있으면 continue.
        Blue Set에 있으면
            값을 비교해서 업데이트 (ShorestDistance + Edge Weight < MaybeShorestDistance) ... (1)
        아니면
            BlueSet에 push한다. (ShortestDistance + Edge Weight, Node)

Find One Path
- …(1) 과정에서 Adject Node에게 나를 업데이트 해준 Node를 기억하게 해주면 된다.
- 그렇게 하면, Node에서 나를 업데이트 해준 Node를 따라가다보면 Source Node가 나오고, 그 자취가 바로 Shortest Path.
Find All Path
- …(1) 과정에서 horestDistance + Edge Weight = MaybeShorestDistance인 경우, 나에게 오는 Shortest Path가 여러개라는 뜻이다.
- 따라서, 둘다 기억한다. 만약 더 짧은 길이 생기면, 이전에 기억해둔 것을 초기화하고 새로운 노드를 기억하면 된다.

C++로 구현한 코드는 다음과 같다.

  
template <typename T>
map<T, int> dijkstra(const Graph<T>& graph, const T& start) {
    // redSet: Node : Shortest Weight Distance
    map<T, int> redSet = { { start, 0 } };
    PriorityQueue<T> blueSet;

    for (const auto& neighbor : graph.getNeighbors(start)) {
        blueSet.push(get<0>(neighbor),
                     get<1>(neighbor));  // node, weight
    }

    while (!blueSet.isEmpty()) {
        int maybeShortestWeight = blueSet.topPriority();
        T currentNode = blueSet.pop();

        // redSet에 이미 있는 노드는 무시
        if (redSet.find(currentNode) != redSet.end()) continue;

        // maybeShortestWeight였던 것을 확정
        redSet[currentNode] = maybeShortestWeight;

        // Update maybeShortestWeight of nodes in blue set
        for (const auto& neighbor : graph.getNeighbors(currentNode)) {
            T node = get<0>(neighbor);
            int weight = get<1>(neighbor);
            blueSet.push(node, maybeShortestWeight + weight);  
  
            // 여기서 currentNode와 neighbor을 사용해서 preTable에 넣으면 될듯.
        }
    }

    return redSet;
}

Deadline Scheduling

Deadline과 Profit을 갖는 Job들을 Time Schedule내에 가장 효율적으로 배치하는 방법. n개의 Job 존재한다. \(J_{i} = \{ (D_{i}, P_{i}) \mid 1 \leq i \leq n \}\) Job은 Deadline과 Profit(이익)의 Tuple이다. 이때 문제 조건은 다음과 같다.

모든 Job을 수행하는데 걸리는 시간은 1이다.
Deadline 이전에 Job을 수행하면 이익 \(P_{i}\)를 얻고, 수행하지 못하면 이익 0.
한번에 하나의 Job만 처리할 수 있음.

목표는, 제한된 Time Schedule내에 가장 많은 Profit을 얻는 것이다. Profit이 큰 순서대로 Job을 정렬해보자. \(P(j)\)는 Job의 Profit을 구하는 함수라고 가정하면, \(P(J_{1}) \geq P(J_{2}) \geq \dots \geq P(J_{n})\)으로 정렬된다. Job을 앞에서부터 순서대로 꺼내고, Job을 처리하는 순간을 딱 Deadline 전에 배치하면 되지 않을까? Deadline이 겹치면 그 앞에 배치하고, 배치할 수 없으면 넘어가고. 이걸 계속 반복하면 되지 않을까?

그리디를 검증해보자. 내가 만들어나가는 Job List \(A\)와, 이미 정답인게 밝혀진 Job List \(S\)가 있다고 가정하자. 총 n개의 Job \(J_{1}\), \(J_{2}\), …, \(J_{n}\)가 존재하고, Profit이 큰 순서대로 정렬되어있다. Job을 Greedy Algorithm을 지키며 A에 추가한다. 만약 S와 A가 같다면 문제 없다.

만약 \(J_{i}\) 를 A에 넣으려 헀더니, S와 A가 달라지면? 일단 알고있는 것은, \(J_{1}, \dots, J_{i-1}\)까지는 A와 S가 동일하고, \(J_{i}\)는 반드시 \(D_{i}\) 전에 추가되어야 한다는 점이다.

Case 1. A에서 \(J_{i}\)를 버렸는데, \(S\)는 갖고있는 경우. \(J_{i}\)를 버렸다는 것은 무슨 의미인가? \(J_{1}, J_{2}, \dots, J_{i-2}, J_{i-1}\) 얘네들이 \(D_{i}\) 이전의 모든 Schedule 공간을 차지하고 있어 넣을 공간이 없는 경우이다. 하지만 \(J_{1}, J_{2}, \dots, J_{i-2}, J_{i-1}\)까지는 A와 S가 동일하기 때문에, 만약 A에서 \(J_{i}\)를 버렸다면 S도 \(D_{i}\) 전까지 스케쥴 공간이 꽉 차있어 \(J_{i}\)를 넣을 자리가 존재하지 않을 것이다. 따라서 모순.

Case 2. A에서 \(J_{i}\)를 넣었는데, \(S\)는 안갖고 있는 경우. 똑같은 논리로, \(J_{1}, J_{2}, \dots, J_{i-2}, J_{i-1}\) 까지는 A와 S가 동일하게 배치되어 있다. A에서 \(J_{i}\)를 넣을 공간이 있다는 것은, S에도 넣을 공간이 있다는 것이다. 만약 S에 추가하면, S는 더 좋은 답이 되버린다. 따라서, 초기에 가정했던 S가 답이라는 조건과 어긋난다. 따라서 모순.

Case 3. A와 S에 둘다 \(J_{i}\)를 넣은 경우 여기서 또 Case를 나눠야 한다.

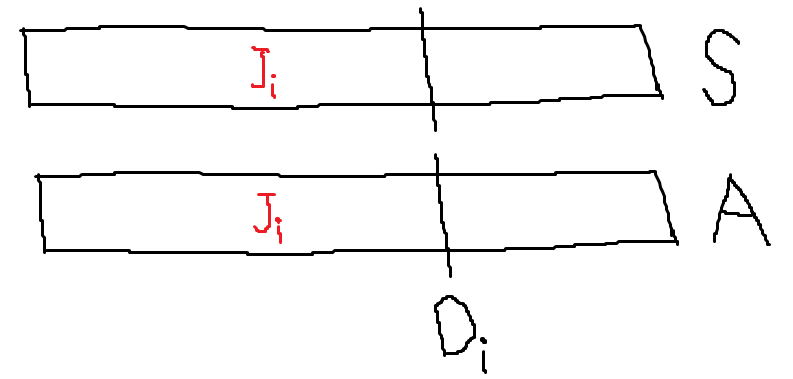
Case 3-1. 똑같은 자리에 \(J_{i}\)를 넣은 경우

이 경우는 문제가 되지 않는다. 따라서 OK.

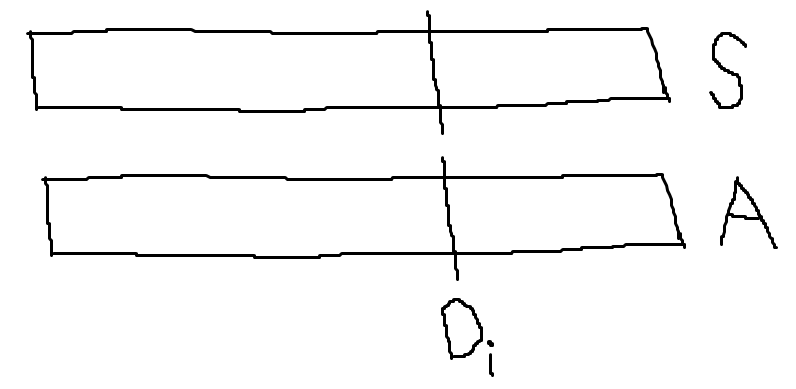
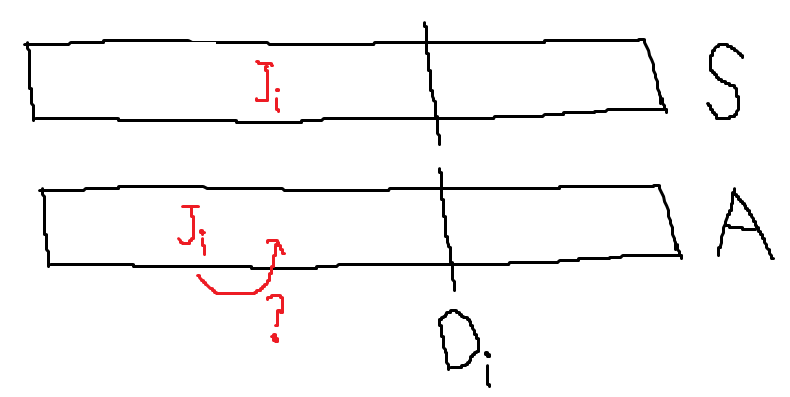
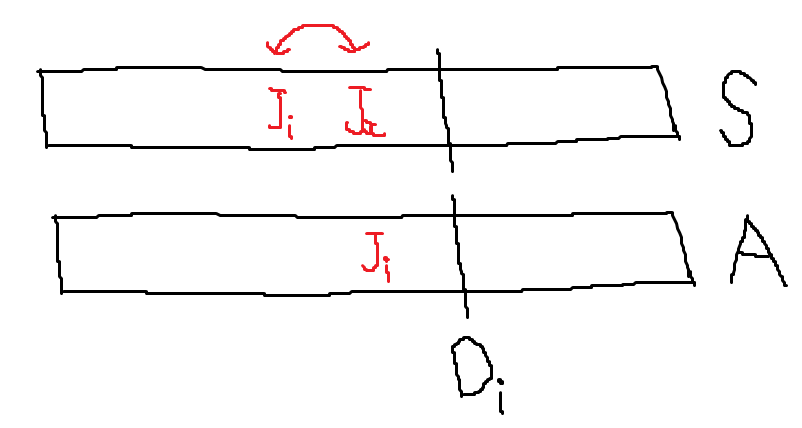
Case 3-2. S에 들어간 \(J_{i}\)보다 A에 들어간 \(J_{i}\)가 앞에 있는 경우

위 그림과 같은 상황은 불가능하다. 왜? S에서 \(J_{i}, J_{i+1}, \dots\)를 다 덜어내면, A와 같아진다. 그러면 S에 있는 \(J_{i}\) 자리가 빈 공간이 될 것이며, A와 S는 동일한 집합이므로 A 또한 저 자리가 빈 공간일 것이다. 따라서 알고리즘은 애초에 A의 \(J_{i}\) 자리가 아닌 그보다 더 뒤에 추가했을 것이다. 따라서 모순.

Case 3-3. S에 들어간 \(J_{i}\)보다 A에 들어간 \(J_{i}\)가 뒤에 있는 경우

똑같이 A의 \(J_{i}\) 자리에 대응되는 S 자리에 있는 Job을 \(J_{x}\)라고 하자. \(J_{x}\) 자리에 Job은 비어있을 수 없다. 만약 비어있다면, S에 \(J_{i}\)를 넣어 더 좋은 답을 만들 수 있기 때문이다. \(J_{x}\)는 \(J_{i}\) 자리에 들어가도 괜찮다. 왜? 스케줄의 뒤로 가는건 데드라인 밖으로 넘어갈 수 있기 때문에 문제가 될 수 있다. 하지만 스케쥴의 앞으로 가는건, 어차피 데드라인 안에서 처리될 작업이기 때문에 문제가 안된다.

반대로, \(J_{i}\) 또한 \(J_{x}\) 자리에 들어갈 수 있다. 왜? \(J_{i}\) 자리는 알고리즘에 의해 Deadline 전이라는 것이 A에 \(J_{i}\)가 추가됨으로써 보장받았기 때문이다. 따라서 Swap 과정을 통해 새로운 정답인 \(S_{new}\)를 만들어낼 수 있다.

위 과정은 모든 과정에 대해 적용할 수 있다. 각 단계에서, Job을 추가한 위치가 다르다면, 교환 과정을 통해 새로운 정답인 \(S_{new}\)를 만들어낼 수 있기 때문이다. 과정이 끝나면, A는 \(S\) 또는 \(S_{new}\)와 동일해진다. 따라서 우리가 만든 Greedy Algorithm이 하나의 정답을 찾아낼 수 있음을 증명한다.

시간 복잡도는 \(O(n^2)\)이다. Balence Tree를 써서 Schedule의 빈 공간을 관리하면 더 빠르게 구현할 수도 있다. 처음에 0부터 n개까지 슬롯을 Tree로 제공하고 \(D_{i}\)보다 같거나 작으면서, 가장 큰 Slot 값을 Query하여 그 슬롯을 꺼내면 Tree에서 Delete하고 Tree가 비면 더이상 Job을 추가할 수 없다는 것과 같다. 이렇게 하면 \(O(NlogN)\)이다.

Job Scheduling

Start Time과 End Time을 갖는 Job들을 Time Schedule 내에 가장 효율적으로 배치하는 방법. \(n\)개의 Job 존재한다. \(J_{i} = \{(S_{i}, E_{i}) \mid 1 \leq i \leq n \}\) Job은 Start Time과 End Time의 Tuple이다. 문제의 조건은 다음과 같다.

모든 Job의 Profit는 동일하다.
한번에 하나씩 Job를 처리 할 수 있다.

목표는, 제한된 Time Schedule 내에 가장 많은 Job을 Schedule하는 것이다. End Time이 짧은 순서대로 Sorting 해보자. 추가할 수 있다면 추가하고, 추가 할 수 없으면 추가하지 않는다. 이걸 계속 반복한다.

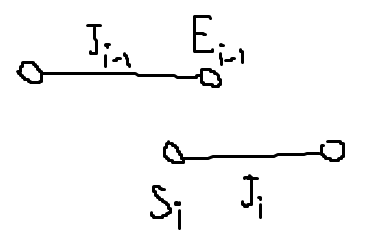
\(J_{i}\)의 \(S_{i}\)가 \(J_{i-1}\)의 \(E_{i-1}\)보다 작으면 추가할 수 없다.
같거나 크면, 추가할 수 있다.
계속 반복한다.

위 그리디 아이디어가 정말 정답을 반환하는지 검증해야 한다. 알고리즘이 만들어 나가는 것을 A, 정답 스케쥴을 S라고 하자. A에 Job을 추가하는데, 그동안 A와 S가 같다면 괜찮다. 만약 \(J_{i}\)를 A에 추가하려고 했는데, S와 달라진다면?

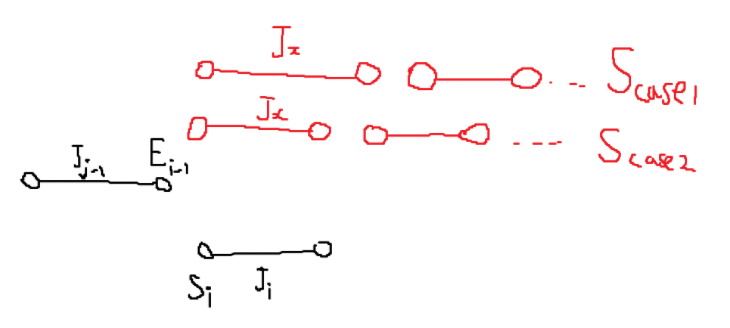
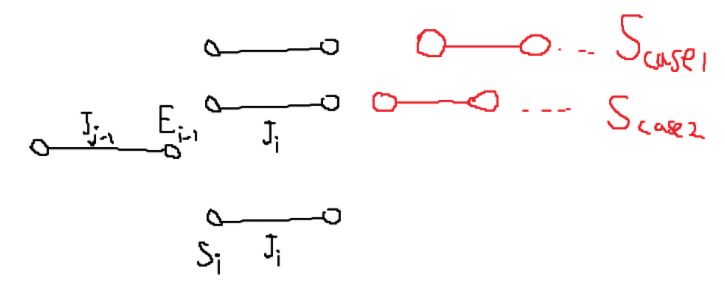
일단 A의 \(J_{i}\)와 충돌하는 S의 Job을 \(J_{x}\)라고 하자. \(J_{x}\)의 End Time \(E_{x}\)는 \(J_{i}\)보다 크거나 같다. 그 이유는, 알고리즘 자체가 End Time이 작은 순서대로 Task를 추가하고 있었기 때문이다. 만약 \(E_{x}\)가 더 작았다면, 애초에 그걸 추가했을 것이다.

두 케이스 모두 S에 있는 \(J_{x}\) 대신 \(J_{i}\)를 넣어도 괜찮다.

따라서 두 케이스 모두 새로운 정답 \(S_{new}\)가 될 수 있다. 위 과정은 모든 과정에 똑같이 적용된다. \(J_{i}\)를 추가하는데, A와 S가 같다면 문제가 없고, 달라진다면 Swap 과정을 통해 새로운 정답 \(S_{new}\)를 만들 수 있다. Greedy Algorithm이 끝나면, A는 \(S\) 또는 \(S_{new}\)와 같아진다. 따라서 우리가 만든 Greedy Algorithm이 하나의 정답을 찾아낼 수 있음을 증명한다.

Tabe Storage

돌돌 감겨있는 테이프는 데이터를 찾으러 가는 과정이 오래 걸린다. 따라서 데이터를 찾으러 가는 시간을 줄이는게 중요하다. 테이프에 어떤 순서로 배치하면 좋을까?

먼저, (1) 큰게 앞에 있으면 안좋다. 작은게 앞에 몰려있을 수록 찾을 확률이 올라갈 것 같다. (2) 자주 쓰는게 앞에 있는게 좋다. 이는 당연하다.

\(i\)번째 데이터 \(D_{i}\)의 크기를 \(L_{i}\), 사용 빈도를 \(F_{i}\)라고 정의하자. \(L\)이 작을수록, \(F\)가 클수록 앞에 있는게 좋겠다. 따라서 \(\displaystyle \frac{F_{i}}{L_{i}}\)을 하나의 가중치로 잡고, 이 가중치대로 배치하면 되겠다.

왜 굳이 가중치를 \(\displaystyle \frac{F_{i}}{L_{i}}\)로 설정하는가? \(\displaystyle \frac{F_{i}^2}{L_{i}^2}\), \(F_{i} - L_{i}\) 이런걸로 가중치를 계산하면 안될까? 일단 데이터를 찾는데 평균적으로 걸리는 시간이 적을수록 좋다. 기댓값^[Expected Value (기댓값)]을 계산해서, 기댓값이 작을수록 좋다.

\(D_{i}\)를 찾을 확률을 \(F_i\)라고 해보자. \(D_{i}\)를 찾을 떄까지 필요한 비용은 데이터를 i번째까지 거쳐야 하므로 \(L_{1} + L_{2} + \dots + L_{i}\)이다. \(\displaystyle \frac{F_{i}}{L_i} < \frac{F_{i+1}}{L_{i+1}}\)라고 하자. 따라서 기댓값은 다음과 같다. \(F_{1}L_{1} + F_{2}(L_{1} + L_{2}) + \dots + F_{i}(L_{1} + L_{2} + \dots + L_{i}) + F_{i+1}(L_{1} + \dots + L_{i} + L_{i+1}) + \dots\)

\(F_{i}\)와 \(F_{i+1}\)의 위치를 스왑하면 다음과 같다.\(F_{1}L_{1} + \dots + F_{i+1}(L_{1} + \dots + L_{i-1} + L_{i+1}) + F_{i}(L_{1} + \dots + L_{i-1} + L_{i+1} + L_{i}) + \dots\)

위에서 아래 값을 빼면 \(\displaystyle F_{i+1} L_{i} - F_{i} L_{i+1} = L_{i}L_{i+1} \left( \frac{F_{i+1}}{L_{i+1}} - \frac{F_{i}}{L_{i}} \right)\)이다. 괄호 안의 값이 양수이므로, 위의 값의 기댓값이 더 크다는 뜻이다. 기댓값이 더 작아질 수 있다는 반례가 존재하므로 \(F_{i}\) 순서대로 배치하면 안된다는걸 알았다. 만약 \(F_{i}\)가 아니라 \(\displaystyle \frac{F_{i}}{L_{i}}\) 순서대로 배치했으면, 두 기댓값의 차이가 \(\displaystyle \frac{F_{i+1}}{L_{i}} L_{i} - \frac{F_{i}}{L_{i+1}} L_{i+1} = 0\)이라 0이므로 \(\displaystyle \frac{F_{i}}{L_{i}}\)로 가중치를 설정하는 것이 최적의 값이다.

IT, 알고리즘

Greedy 알고리즘 최소 신장 트리 Prim 알고리즘 Kruskal 알고리즘 다익스트라 알고리즘 작업 스케줄링 기댓값