알고리즘 1. Basic Algorithm
건국대학교 알고리즘 김성열 교수님의 수업을 정리한 내용입니다.
Sorting
정렬 알고리즘의 경우 일반적으로 비교 정렬을 사용하고, 특정 조건이 만족되는 경우 Counting Sort, Radix sort같은 알고리즘을 사용할 수 있다.
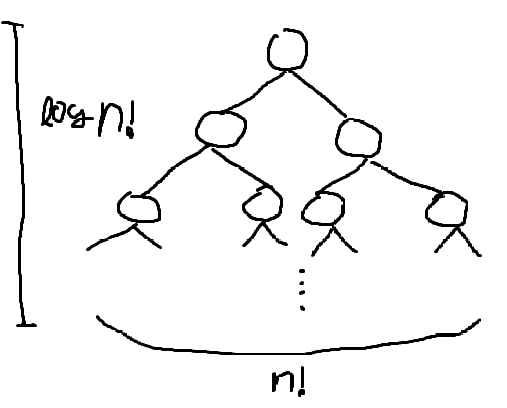
비교 정렬 알고리즘의 경우 \(O(n\log n)\)보다 빠를 수 없다. 그 이유는, 비교하는 선택지를 결정 트리로 만들면 Leaf 노드의 개수는 \(n!\)일 것이고 결정 트리의 높이는 최소 \(\log n!\)이다. 비교하여 정렬한다는 것은 Root에서 시작하여 정렬된 상태의 Leaf 노드를 찾는 것과 같고 시간 복잡도는 \(O(\log(n!))\)이다. \(n!\)은 Stirling’s Approximation (스털링 근사)를 사용하여 \(\displaystyle n! \simeq \sqrt{ 2\pi n } \left( \frac{n}{e} \right)^n\)로 근사할 수 있으므로, \(\log n!\)은 \(\displaystyle \log n! \simeq n\log n - n + \frac{1}{2} \log(2\pi n)\)로 근사할 수 있다. 양 변에 Big-O Annotation을 적용하면 \(\displaystyle O(\log(n!)) \simeq O\left( \log\left( \sqrt{ 2\pi n } \left( \frac{n}{e} \right)^n\right) \right) \simeq O(n\log n)\)와 같다. 따라서 비교 정렬 알고리즘의 Lower Bound는 \(O(n\log n)\)이다.
Selection Sort
전체를 한번 탐색하여 가장 작은 값을 맨앞으로 보낸다. 다음 칸에서 시작하여 다시 한번 탐색하고, 가장 작은 값을 두번째로 보낸다. 이를 반복한다. \(O(n^2)\) 시간이 걸린다. 반복문으로 구현하면 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
void selectionSort(int *array, int array_size)
{
if (array_size <= 1) return;
int minium_index = 0;
for (int index = 0; index < array_size; index++) {
for (int k = index; k < array_size - 1; k++) {
if (array[k] < array[minium_index])
minium_index = k;
}
swap(array[index], array[minium_index]);
}
}
[!tip]- 정확성 증명{title} 증명해야 하는 것
- sorting 이후 array는 다음 조건을 만족해야 한다 .a[0] < a[1] < … < a[n-1] < a[n], n = item count in array
Invariant: 반복문의 한 단계가 끝날 때마다, array[0:index]는 정렬되어 있다.
초기: array[0:0]은 정렬됨이 자명하다. 유지: array[index:N-1] 사이의 최소값을 찾아, index 자리와 swap한다. 이 행동이 Invariant를 유지시켜 준다. « 여기가 좀더 엄밀하게 수학적 귀납법으로 증명되야할 거 같은데? 종료: 반복문이 종료되면, index는 N과 같다. Invariant에 따라, 배열 array[0:N]은 정렬되었다.
재귀로 구현하면 다음과 같다. 시간 복잡도는 \(T(n)=n+T(n-1) = n+n-1+T(n-2) = \dots = O(n^2)\)와 같이 계산할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
void selectionSort_recursion(int *array, int array_size)
{
if (array_size <= 1) return;
for (int index = 0, minium_index = 0; index < array_size; index++) {
if (array[index] < array[minium_index])
minium_index = index;
}
swap(array[0], array[minium_index]);
selectionSort_recursion(array + 1, array_size - 1);
}
[!tip]- 정확성 증명{title} Base: N=1이면, 정렬됨이 자명하다. Step
- Sort(array[1:N-1])이 True라고 가정하자.
- array 내의 값을 한번 순환하여, 최솟값을 찾고 그 값을 array[0]과 swap한다.
- 이후 Sort(array[1:N-1])를 하면, array[0:N]이 모두 정렬된다.
- 따라서 Sort(array[0:N])의 결과는 True다.
따라서 수학적 귀납법에 의해 Sort(array)는 항상 참인 값을 반환한다.
Merge Sort
입력된 배열을 두개로 나눠서 각각 정렬하고, 정렬된 두 배열을 Merge한다. Divide and Conquer를 적용한 정렬 방법이다. Merge 방법은 두 배열의 모든 값이 빌 때까지 다음 과정을 반복하면 된다.
- 두 배열의 맨 앞의 값을 비교하여 작은 값을 뽑는다.
- 뽑은 값을 결과 배열에 추가한다.
시간 복잡도와 공간 복잡도는 각각 다음과 같다.
- \(\displaystyle T(n) = n + 2T\left( \frac{n}{2} \right) = n + 2\left( \frac{n}{2} + 2T\left( \frac{n}{4} \right) \right) = ... = O(n \log n)\)
- \(n + \log n \implies O(n)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void mergeSort(int* array, int array_size)
{
if (array_size <= 1) return;
int half_array_size = array_size / 2;
int copy_array[array_size];
copy(array, array + array_size, copy_array);
// 앞에 절반, 뒤에 절반 sort
mergeSort(copy_array, half_array_size);
mergeSort(copy_array + half_array_size, array_size - half_array_size);
// 이후 앞에 절반, 뒤에 절반 합치기
int front_index = 0, back_index = half_array_size;
for (int index = 0; index < array_size; index++) {
if (front_index == half_array_size - 1) { // 앞에 원소를 다 뽑았다면
array[index] = copy_array[back_index];
back_index += 1;
} else if (back_index == array_size - 1) { // 뒤에 원소를 다 뽑았다면
array[index] = copy_array[front_index];
front_index += 1;
} else {
if (copy_array[front_index] < copy_array[back_index]) {
array[index] = copy_array[front_index];
front_index += 1;
} else {
array[index] = copy_array[back_index];
back_index += 1;
}
}
}
}
[!tip]- 정확성 증명{title}
Tool: sort 부분엔 수학적 귀납법, merge 부분엔 Loop 불변성으로 하면 될듯?
n/2일 떄 sort() 함수가 성공한다면, => 즉 재귀 호출이 끝난 후 b[0] « b[2] < … < b[n/2-1] and b[n/2] < 일 때 n일 때 sort() 함수가 성공한다.
1) Sort 증명
Suppose: Merge 부분을 일단 True라고 가정하자. Let: half array = a[0:m] or a[m:n] Base: n = 1이면, array는 이미 sort되었다. 따라서 True Step:
- mergeSort(half array, n / 2)가 True라고 가정하자.
- ca[] copy to a[], ca[]를 절반 범위로 나눠서 Merge(ca[0:m], m), mergeSort(ca[m+1:n], n-m)으로 Sorting한다.
- 이후 Sorting한 범위를 서로 Merge하면 전체 Sorting된 배열이 된다.
따라서, mergeSort(half array, n/2)가 True일 때 mergeSort(array, n)이 True이므로 이 알고리즘은 자연수 n일때 True이다.
2) Merge 증명
Invariant. 반복이 한번 끝날때마다, a[0:i]는 정렬되어있다.
Let 1. (앞에 정렬된 배열을 순회하는 Index) = fi = front_index Let 2. (뒤에 정렬된 배열을 순회하는 Index) = bi = back_index Let 3. a[0:n] = a[0] ~ a[n-1]
초기: i = 0이고, a[0:0]은 정렬됨이 자명하다. 따라서 Invariant를 해치지 않는다. 유지: 앞에서 원소를 다 뽑았거나 (
equal fi ** m), 뒤에서 원소를 다 뽑았다면 (equal bi ** n) 뒤에 있는 ca의 원소들 또는 앞에 있는 ca의 원소들을 그대로 a에 덮어쓴다. 이 경우 ca[bi] 또는 ca[fi]를 그대로 a[i]에 넣으며, Invariant를 유지시킨다. 아니라면, 두 배열의 앞에 있는 값 중 더 작은 값을 a[i]에 삽입한다. 이는 작은 값이 앞에서부터 오게 하며, Invariant를 유지한다. 종료: 반복이 종료되면, i = n이 되며, Invariant가 깨지지 않았다. 따라서 a[0:n]은 정렬되었다.
Quick Sort
입력으로 들어온 배열의 값 중 아무거나 기준을 하나 잡는다. 그 기준을 \(p\)라고 하면, \(p\)보다 작은 값은 \(p\)의 왼쪽, \(p\)보다 큰 값은 \(p\)의 오른쪽으로 옮긴다. 만약 \(p=a[0]\)으로 잡는다고 하면, 구현은 탐색 Pointer i, j를 만들어서 할 수 있다.
 i는 앞에서부터 p보다 큰 값을 탐색하고, j는 뒤에서부터 p보다 작은 값을 탐색한다. 하나씩 값을 찾았다면 \(a[i]\)와 \(a[j]\)의 값을 Swap한다. \(j\leq i\)가 될 때까지 반복한다.
i는 앞에서부터 p보다 큰 값을 탐색하고, j는 뒤에서부터 p보다 작은 값을 탐색한다. 하나씩 값을 찾았다면 \(a[i]\)와 \(a[j]\)의 값을 Swap한다. \(j\leq i\)가 될 때까지 반복한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void qsort(int a[], int n) {
int pivot = a[0];
int i = 1;
int j = n - 1;
while (i <= j) {
while (i <= j && a[i] <= pivot) i++; // 왼쪽에서 pivot보다 큰 값을 찾음
while (i <= j && a[j] > pivot) j--; // 오른쪽에서 pivot보다 작은 값을 찾음
if (i < j) {
std::swap(a[i], a[j]); // 두 값을 교환
}
}
std::swap(a[0], a[j]);
qsort(a, j); // 왼쪽 부분 정렬
qsort(a + j + 1, n - j - 1); // 오른쪽 부분 정렬
}
\(p\) 값이 어떻게 선택되냐에 따라서 시간이 느려지고 빨라지고 할 수 있다. 최악의 경우는 \(q\)값이 항상 가장 작인값이 선택면 \(O(n^2)\)이고, 최고의 경우 \(q\)값이 항상 중앙값이 선택되어 \(O(n\log n)\)이다. 평균 시간 복잡도는 \(O(n\log n)\) 시간이 걸리고 실험해봤을 때 Merge Sort보다 더 빠르다고 알려진다.
[!tip]- 평균 시간 복잡도 계산{title} p를 k번째 값으로 선택할 경우, 시간복잡도는 다음과 같다. \(T(n) = n + T(k-1) + T(n-k)\) n = 전체적으로 한번 순회하는 시간 T(k-1) = k의 왼쪽 부분 정렬 T(n-k) = k의 오른쪽 부분 정렬
평균을 생각해보자. 즉, 기댓값을 계산해야 한다. p를 1, 2, …, k, …, n-1, n을 잡았을 때를 사건으로 생각하고, 각 사건의 시간 복잡도를 계산하여 n으로 나누면 기댓값을 계산할 수 있다.
\[\displaystyle T(n) = \frac{1}{n} \sum_{k=1}^n (n + T(k-1) + T(n-k))= \sum_{k=1}^n n + \sum_{k=1}^n T(k-1) + \sum_{k=1}^nT(n-k)\]\(\displaystyle \sum_{k=1}^n T(k-1) = T(0) + T(1) + \dots + T(n-1)\) \(\displaystyle \sum_{k=1}^n T(n-k) = T(n-1) + \dots + T(1) + T(0)\) 둘의 값이 같다. \(\displaystyle \therefore ~ T(n)= n + \frac{2}{n} \sum_{k=1}^{n-1} T(k)\) 이때, \(T(0) = 0\)이므로 이 값은 배제한다.
\(n \to n-1\)을 넣으면 \(\displaystyle T(n-1) = (n-1) + \frac{2}{n-1} \sum_{k=1}^{n-2}T(k)\)
\(\displaystyle nT(n) - (n-1)T(n-1) = n\left( n + \frac{2}{n} \sum_{k=1}^{n-1} T(k) \right) - (n-1)\left( (n-1) + \frac{2}{n-1} \sum_{k=1}^{n-2}T(k) \right)\) \(\displaystyle = n^2 - (n-1)^2 + 2 \sum_{k=1}^{n-1}T(k) - 2\sum_{k=1}^{n-2}T(k) = 2n-1 + 2T(n-1)\) \(\displaystyle \implies nT(n) = (n+1)T(n-1) + 2n-1\) \(\displaystyle \implies \frac{T(n)}{n+1} = \frac{T(n-1)}{n} + \frac{2n-1}{n(n+1)}\) \(\displaystyle \implies \frac{T(n)}{n+1} = \frac{T(n-1)}{n} + \frac{3}{n+1}-\frac{1}{n}\)
재귀적으로 대입하면 다음과 같다. \(\displaystyle = \frac{3}{n+1} - \frac{1}{n} + \frac{3}{n} - \frac{1}{n-1} + \frac{3}{n-1} - \frac{1}{n-2} + \dots\) \(\displaystyle = \frac{3}{n+1} + 2\left( \frac{1}{n} + \frac{1}{n-1} + \dots + \frac{1}{2} + \frac{1}{1} \right)\) \(\displaystyle = 2\left( 1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n-1} + \frac{1}{n} \right) + \frac{3}{n+1}\) \(\displaystyle \implies T(n) = (n+1)\left( 1+\frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n} \right) + 3\)
이때, \(\displaystyle \sum_{k=1}^n \frac{1}{k}\)는 \(\ln x\)로 근사할 수 있다.^[조화 급수를 근사하는 방법] \(T(n) = (n+1) \log n + 3 = O(n\log n)\)
Counting Sort
만약 들어올 데이터 타입을 이미 알고있다면, 입력된 값을 한번 순회하면서 갯수를 세서 다시 나열하면 된다. 이 경우 시간이 \(O(n)\)만에 정렬이 가능하다.
Radix Sort
비교정렬이 아닌, 입력값이 문자열과 같이 예상되는 범위 내이고, 단위가 크면 효과적이다.
[!tip] Idea : 만약 사전 100만개를 직접 정렬하라고 하면 어떻게할래?{title} a로 시작하는거, b로 시작하는거, …, z로 시작하는거를 따로따로 모은다.
이후, a 중 두번째 글자가 a, b, …, z b 중 두번째 글자가 a, b, …, z
이렇게 또 분류한다.
[!error] 구현할 때 주의!{title} 단어를 직접 복사하지 말고, 주소값을 다뤄야 한다.
Binary Search
정렬된 배열에서 중앙값부터 시작하여 절반씩 탐색 범위를 줄여가는 Search 알고리즘. 시간은 \(O(\log n)\)만에 Search 가능하다. 반복문으로 구현한 것은 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int binarySearch(int *sorting_array, int target)
{
int left, middle = 0;
int right = _msize(sorting_array) - 1;
while (left <= right) {
middle = (left + right) / 2;
if (sorting_array[middle] < target)
left = middle + 1;
else if (sorting_array[middle] > target)
right = middle - 1;
else
return middle;
}
return -1;
}
[!tip]- 정확성 증명{title} Invariant 1. left <= middle <= right Invariant 2. left <= right
초기화:
반복문이 시작할 때 초기조건이 Invariant를 해치지 않음을 보여라.left = 0, right = array size - 1, middle = left + right. array size > 0이면 Invariant 1과 2가 항상 참이고, 가질 수 있는 최소값의 array size = 0인 경우도 Invariant 1, 2가 만족된다.유지:
반복문이 진행되어도 Invariant가 깨지지 않음을 보여라middle은 항상 반복문 초반에 left와 right의 중간값으로 정의된다. left와 right값이 바뀌는 경우는 두가지가 있는데, array[middle] < target인 경우 값은 array[0] ~ array[middle] 사이에 존재할 수 없으므로, 탐색범위를 left=middle+1~right로 좁힌다.반대로 array[middle] > target인 경우 값은 array[middle] ~ array[right] 사이에 존재할 수 없으므로, 탐색범위를 left ~ right = middle - 1로 좁힌다.
종료:
Invariant가 깨지지 않고 반복문이 종료되면, 원하는 목적을 수행함을 보여라.left와 right 사이의 거리는 반복문이 진행 될 때마다 항상 좁아지며, 중간에 target 값을 찾거나, 완전히 좁혀져 target 값을 찾으면 i를 리턴하고, 그렇지 않으면 반복문 조건에서 벗어나 -1를 리턴한다.
재귀로 구현한 버전은 다음과 같다. 공간 복잡도가 함수 호출 스택때문에 \(O(\log n)\)이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int binarySearch_recursion(int *sorting_array, int array_size, int target)
{
if (array_size == 0) return -1;
int middle = array_size / 2;
if (sorting_array[middle] < target) {
int result = binarySearch_recursion(sorting_array + middle + 1, array_size - (middle + 1), target);
if (result == -1) return result;
else return result + middle + 1;
}
else if (sorting_array[middle] > target)
return binarySearch_recursion(sorting_array, middle, target);
else
return middle;
}
[!tip]- 정확성 증명{title} Base Condition: n = 0이면, x의 값은 존재할 수 없다. 따라서 return -1, 알고리즘은 True. Let: half array = a[0:m] or a[m:n] Step: 1. 함수 BS(ahalf array, n/2, target)가 True라고 가정하자. 2. a[m] < target이면, BS(a[m+1:n], n-(m+1), target) 값을 가져온다. 반환값이 -1이라면, 왼쪽 위에도 값이 없고 오른쪽 범위에도 없으므로 array에는 값이 없다. 따라서 -1 반환. vaild index를 반환했다면, return i + (m+1) 4. a[m] > target이면, BS(a[0:m], m, target) 값을 그대로 반환한다. vaild index를 반환했다면 array의 시작점이 같으므로 곧 전체 index와 갇고, -1를 반환헀다면 왼쪽 오른쪽 범위 모두 없으므로 -1를 그대로 반환해야 한다. 5. a[m] = target이면, i = m이므로 return m.
즉 BS(half array, n/2, target)가 True라고 가정했을 때, BS(a[0:n], n, target)가 True이므로 위 알고리즘은 모든 자연수 n에서 참이다.