수리물리학 5. Vector Calculus

Mathematical Methods in the Physical Sciences, Mary L. Boas의 5장 내용입니다.

Line Integral

open path는 시작과 끝점이 있는 path, close path는 경로가 닫힌 path를 의미한다. 선적분을 하기 위해 \([a,b]\to C\)로 가는 변환 함수 \(\vec{r} = \vec{r}(t) = (x(t),y(t),z(t))\)라는걸 반드시 찾아야 함. 만약 곡선 \(C\)가 \(x=y^2\) 위의 곡선이라면 \(\vec{r}(t)=(t^2,t)\)어야 저 조건을 만족하므로 이런 매개변수방정식을 만들어 공간을 변환할 수 있다. 만약 찾기 무지 어려우면 Spline^[고급컴퓨터그래픽스 1. Curves]으로 근사 곡선을 찾을 수도 있겠다.

\[\int_{C} \vec{A}(\vec{r}) \cdot d\vec{r} = \int^{t_{1}}_{t_{0}} \vec{A} (\vec{r}(t)) \cdot \frac{d\vec{r}}{dt} dt = \int^{t_{1}}_{t_{0}} \vec{A}(\vec{r}(t)) \cdot\vec{r}'(t) dt\]

만약 \(\vec{A}(x,y)=(A_{x}(x,y), A_{y}(x,y))\)라면 실제로 점곱과 같이 연산할 수 있다.

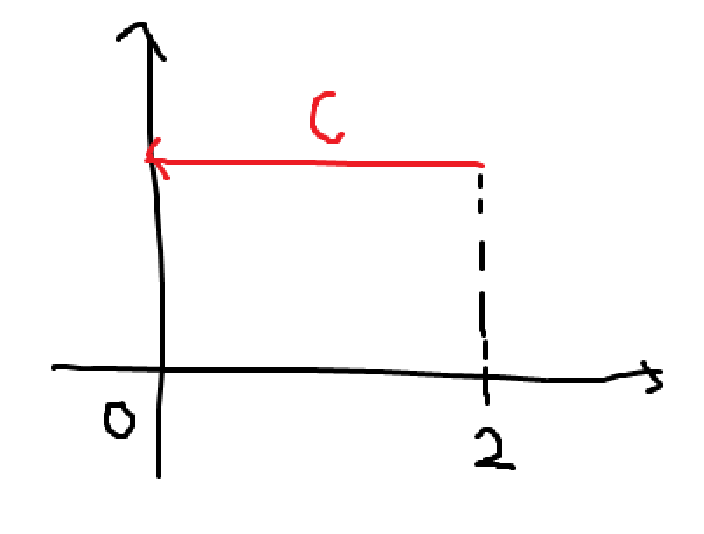
\[\int_{C} \vec{A}(x,y) \cdot d\vec{r} = \int_{C} A_{x}dx + A_{y}dy\]

선적분의 경로가 헷갈린다면, \(C\)의 경로를 평범한 경로로 바꾼 경로 즉 \(-C\)를 계산하고 원래대로 돌렸을 때 부호가 어떻게 붙는지 생각해보면 된다. 예로, 위 그림의 경로를 선적분하는데 부호와 적분 범위가 헷갈린다면, 바로 C를 적분하지 말고 \(-C\)를 적분해서 -를 붙여보라.

\[\int_{C} \vec{F} \cdot d\vec{r} = -\int_{-C}\vec{F} \cdot d\vec{r} = -\int_{0}^2 (F_{x}, F_{y}) \cdot (dx, 0) = -\left[ \int_{0}^2 F_{x}dx \right]_{y=1}\]

Surface Integral

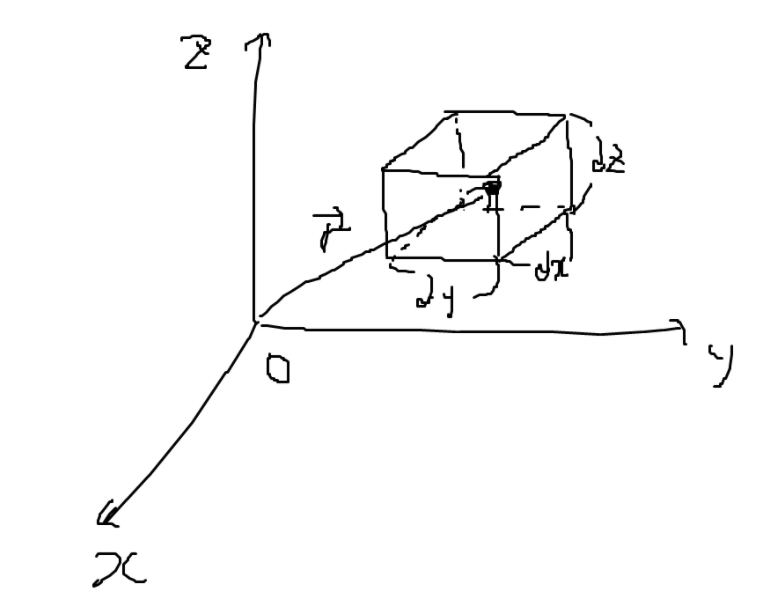
대부분의 Surface는 윗면, 아랫면이 존재하고 이것은 내가 임의로 정해줘야 한다. 미소 면적소는 \(da\)이다. 윗면 아랫면을 구분하여 방향까지 준 면적소는 \(d\vec{a} = \hat{n} da\)이다. 닫힌 곡면 (Closed surface)는 항상 윗면과 아랫면이 구분되고, 이때 \(\hat{n}\)를 바깥으로 나가는 방향으로 약속한다.

Gradiant

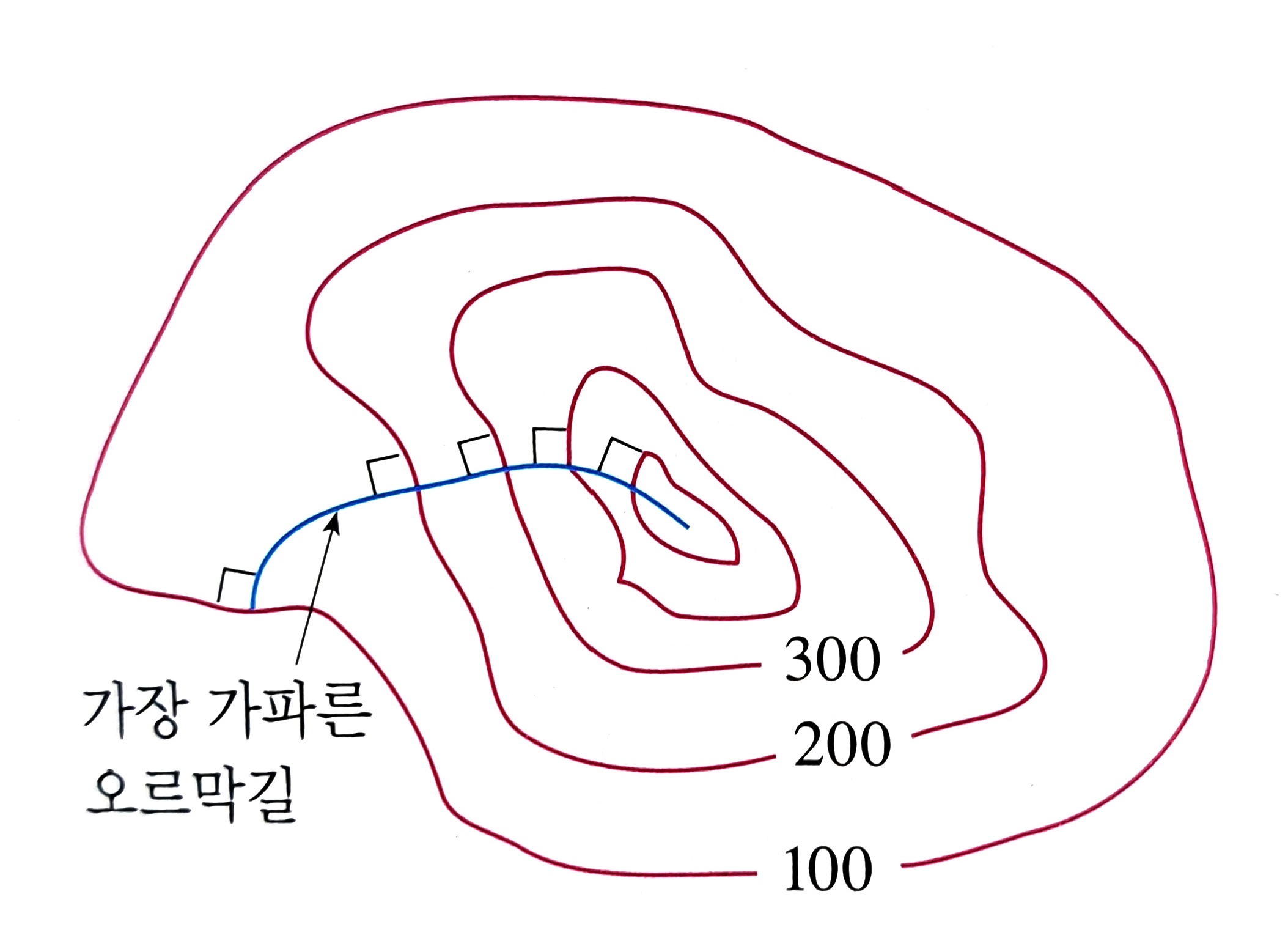
\[\text{Gradiant}~f = \nabla f = \displaystyle (\frac{{\partial f}}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z})\]

스칼라 함수 \(f\)를 넣으면 그 지점에서 함수값이 가장 가파르게 증가하거나 감소하는 방향을 가리키는 기울기 벡터를 반환한다.

\(df\)는 함수 \(f\)의 각각의 축 방향으로 찔끔씩 변화한 양의 합, 즉 \(\displaystyle \frac{{\partial f}}{\partial x} dx + \frac{{\partial f}}{\partial y} dy + \frac{{\partial f}}{\partial z} dz\) 와 같으므로 일반적인 함수의 미소 변화량은 \(df=\nabla f \cdot d\vec{r}\)로 나타낼 수 있다는 중요한 성질이 있다.

\(\nabla f\)를 통해 얻어낼 수 있는 정보는 두가지가 있다.

1. \(\nabla f\)는 \(f\)의 Level Curve, Surface의 수직 방향이다.
2. \(\nabla f\)의 방향은, 함수의 변화량이 가장 큰 방향이다.

1번을 응용하면, \(\nabla f\)를 구해서 벡터들을 그려보고, 벡터의 수직하도록 선을 그려보면 Level Curface, Surface를 쉽게 그릴 수 있겠다. Level Curve, Surface를 그리다 보면 함수 \(f\)가 어떤 모양인지도 유추할 수 있게 된다.

왜 \(f\)의 Level Surface와 \(\nabla f\)가 수직한가? 함수가 \(f(x,y)\) 꼴이라면 곡면이 표현되며 함수값이 같은 점을 모으면 \((f(x,y)=c)\) Level Curve가 만들어진다. 함수가 \(f(x,y,z)\) 꼴일 때 같은 점을 모으면 Level Surface가 만들어진다. Level Curve, Surface 상에서 변하는 \(df\)는 당연히 0이다. \(df = \nabla f \cdot \vec{r} = 0\)이고, 내적한 값이 0이면 두 벡터가 수직하다는 것과 같다.

왜 \(\nabla f\)의 방향은 함수의 변화량이 가장 큰 방향인가? \(df = \nabla f \cdot d\vec{r} = \lvert \nabla f \rvert \lvert d\vec{r} \rvert\cos \theta\)이고, \(df\)가 가장 큰 방향은 \(\nabla f\)와 \(d\vec{r}\)가 평행한 경우이다. 즉, 변화가 \(\nabla f\) 방향으로 이루어질 때 \(df\)가 최대가 된다.

두 정보를 통해 Gradient 벡터의 방향은 항상 곡면의 최고 언덕 또는 최저 계곡을 향한다는 것을 알 수 있다. 이를 통해 최저값, 최대값을 찾을 수 있다는 아이디어로도 이어질 수 있다.

Curl

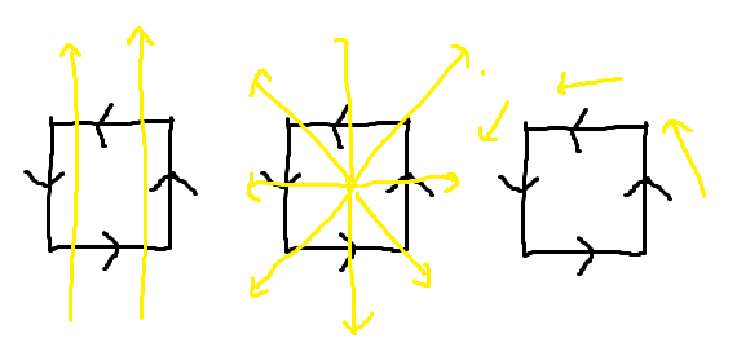
Curl이란, Vector Field의 회전량을 감지하는 도구다. 어떤 Vector Field에 Curl을 취한다는 것은, 어떤 지점에서 \(\vec{A}\)가 얼마나 회전하는지를 나타내는 벡터를 반환하는 함수를 만들어준다. 회전의 방향은 오른손 법칙으로 결정되며, 소용돌이의 세기는 벡터의 세기와 같다. 계산은 다음과 같이 가능하다. \(\nabla \times \vec{A}= \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ A_x & A_y & A_z \end{vmatrix}\)

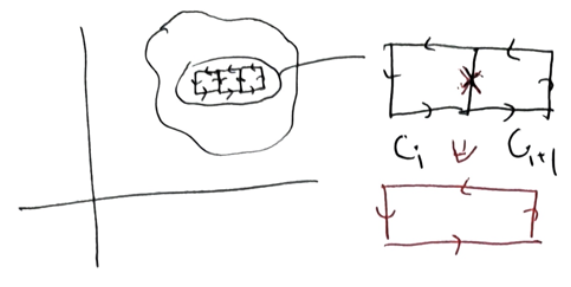
Curl은 벡터장이 돌아가는지 아닌지 작은 네모가 감지해내는 것이다. 만약 1, 2번 그림과 같은 경우 선적분한 값이 서로 상쇄되면서 작은 네모의 값이 0이 만들어진다. \(\displaystyle \oint_{ \text{ㅁ}} \vec{F} \cdot d\vec{r} = 0\)이므로, \(\nabla \times \vec{F}\)가 0과 같다. 선적분의 값이 작은 네모에서 상쇄되지 않으려면, 벡터장이 회전하는 성분이 있어야 하고, 그 때 \(\displaystyle \oint_{ㅁ} \vec{F} \cdot d\vec{r}\)는 0이 아니다.\(\displaystyle \oint_{ㅁ} \vec{F} \cdot d\vec{r} = (\nabla \times \vec{A}) \cdot d\vec{a}\)와 같은 관계가 있으므로, \(\nabla \times \vec{A}\)가 회전 성분을 감지해낼 수 있는 것이다.

Green’s Theorem, Stokes’ Theorem

미분된 함수를 적분하는 것은, 경계값과 같다. 벡터 함수의 미분은 \(\displaystyle \frac{d}{dx}\), \(\nabla\), \(\nabla \cdot\), \(\nabla \times\) 등등이 존재하고 각각 미적분학의 기본정리, 기울기의 기본정리, 발산의 기본정리, 회전의 기본정리로 불리운다. 이때 회전의 기본정리에 해당하는것이 바로 Green’s Theorem, Stokes’ Theorem이다.

• Green’s Theorem : \(\displaystyle \int_{S} ( \partial_{x} A_{y} - \partial_{y}A_{x} )da = \oint_{\partial S} \vec{A} \cdot d\vec{r}\)
• Stokes’ Theorem : \(\displaystyle \int_{S} (\nabla \times \vec{A}) \cdot d \vec{a} = \oint_{\partial S} \vec{A} \cdot d \vec{r}\)

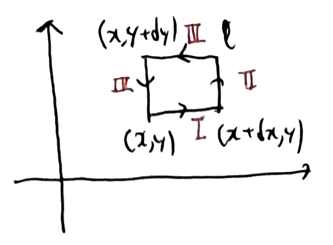
[!tip]- 증명{title} \((\nabla \times \vec{A}) \cdot d \vec{a}\)는 작은 네모 하나의 회전량과 같은데, 이것을 다 더한다면 미소 사각형이 겹치는 부분은 서로 상쇄되고, 최종적으로 경계값만 남게 된다. 그린 정리를 증명하기 위해, 하나의 미소 사각형을 적분하고, 임의의 평면을 미소 사각형으로 잘게 쪼개어 더한것을 생각해보자.

\[\oint_{\Box} \mathbf{F} \cdot d\mathbf{r} = \int_{\mathrm{I}} + \int_{\mathrm{II}} + \int_{\mathrm{III}} + \int_{\mathrm{IV}}\] \[\int_{\mathrm{I}} + \int_{\mathrm{III}} = \int_x^{x+d x} (F_x(x', y) \, - F_{x}(x', y+dy))dx' = - \int_x^{x+d x} \frac{\partial F_x}{\partial y} \, dy \, dx' = -\frac{\partial F_x}{\partial y} \, dx \, dy\] \[\int_{\mathrm{II}} + \int_{\mathrm{IV}} = \int_y^{y+'\Delta' y} \big(F_y(x+d x, y') - F_y(x, y')\big) \, dy'= \int_y^{y+d y} \frac{\partial F_y}{\partial x} \, dx \, dy' = \frac{{\partial F_{y}}}{\partial x}dxdy\]

위 과정에서 ‘구간이 아주 작은 적분은, 그냥 dx를 곱한것과 같다.’ 를 사용한다. 따라서 \(\displaystyle \oint_{\Box} \mathbf{F} \cdot d\mathbf{r} = \left(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}\right) \, dx \, dy\) 결론을 얻는다.

이제 임의의 곡면 S를 미소 사각형으로 쪼개어 생각해보자. 사각형이 겹치는 부분은 사라지고, 최종적으로 경계값만 남게된다.

\[\sum_{i} \oint_{C_i} \mathbf{F} \cdot d\mathbf{r} = \sum_{i} \left( \frac{\partial F_y(x_{i},y_{i})}{\partial x} - \frac{\partial F_x(x_{i},y_{i})}{\partial y} \right) dx_i \, dy_i\]

이때, \(dx_{i}dy_{i}=dA_{i}\)이므로 최종적으로 다음 결과를 얻을 수 있다.

\[\therefore ~ \displaystyle \oint_{C} \mathbf{F} \cdot d\mathbf{r} = \iint_{S} \left( \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right) \, dA\]

미소 사각형의 선적분 값을 구하는 과정을 똑같이 y-z, z-x 평면에 대해 적용할 수 있다. x-z 평면이 아닌 z-x 평면인 이유는, 오른손 법칙에 의해 y가 + 방향이 되도록 순서를 적용한 것이다.

\[\oint_{\Box} \mathbf{F} \cdot d\mathbf{r} = \int \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} \right) \, dy \, dz\] \[\oint_{\Box} \mathbf{F} \cdot d\mathbf{r} = \int \left( \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x} \right) \, dz \, dx\]

\(dydz\)는 \(\hat{x}\)성분, \(dzdx\)는 \(\hat{y}\)성분, \(dxdy\)는 \(\hat{z}\) 성분이므로 이것을 이용해 하나의 Operator를 정의한다.

\[\nabla \times \mathbf{F} = \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} \right) \mathbf{i} + \left( \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x} \right) \mathbf{j} + \left( \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right) \mathbf{k}\]

따라서, 미소 사각형의 선적분 결과를 다음과 같이 일반적으로 표현할 수 있다.

\[\oint_{\Box} \mathbf{F} \cdot d\mathbf{r} = \left( \nabla \times \mathbf{F} \right) \cdot d \vec{a} = \left( \nabla \times \mathbf{F} \right) \cdot \hat{n} \, dA\]

Vector Field \(\vec{F}\) 위에서 미소 사각형을 선적분한 결과가 \(\left( \nabla \times \mathbf{F} \right) \cdot d\vec{a}\)임을 이용하여 Stokes’ Thoream을 유도해낼 수 있다. 일반적인 곡면 S를 각각의 미소 사각형 \(C_{i}\)로 쪼갠 상황을 생각해보자.

\[\sum_{i} \oint_{C_i} \mathbf{F} \cdot d\mathbf{r}_i = \sum_{i} \left( \nabla \times \mathbf{F} \right) \cdot d\mathbf{S}_i\] \[\implies \oint_{C} \mathbf{F} \cdot d\mathbf{r} = \iint_{S} \left( \nabla \times \mathbf{F} \right) \cdot d \vec{a}\]

Simply Connected Region

닫힌 영역의 경계를 한없이 줄여서 한 점으로 만들 수 있을 때, 그 영역을 Simply Connected Region라고 한다. 만약 영역 내의 구멍이 존재한다면, 줄였을 때 한 점으로 만들 수 없다. 따라서, 영역에 구멍이 존재하는 경우 Simply Connected Region가 아니다.

Conservative Vector Field

Vector Field \(\vec{A}\)의 Domain이 Simply Connected Region이고, 모든 구간에서 연속이라면, \(\nabla \times \vec{A} = 0\)일 때 \(\vec{A}\)는 Conservative Vector Field이다.

아래 두 사실은, Domain에 관계 없이 항상 사용 가능하다. \(\displaystyle \oint_{C} \vec{A} \cdot d\vec{r} = 0\)일 때 \(\vec{A}\)는 Conservative Vector Field이다. 역이 성립한다. \(\vec{A} = \nabla f\)를 만족하는 어떤 Scalar Field \(f\)가 존재하면, \(\vec{A}\)는 Conservative Vector Field이다. 역이 성립한다.

따라서, 다음 중 하나만 성립하면 나머지 성질이 자동으로 성립한다.

1. \(\vec{A}\)가 Conservative Vector Field이다. \(\iff \displaystyle \oint_{C} \vec{A} \cdot d\vec{r} = 0\)
2. \(\vec{A} = \nabla f\)를 만족하는 어떤 Scalar Field \(f\)가 존재
3. if \(\vec{A}\) Domain is Simply Connected Region, then \(\nabla \times \vec{A} = 0\)

[!note]- 연관성 증명{title}

1. 1->2 증명 임의의 기준점 O에 대하여 함수 f를 \(\displaystyle f(\vec{r}) = \int^{\vec{r}}_{O} \vec{A}(\vec{r}) \cdot d\vec{r}\)로 정의하자.

\[\displaystyle\oint_{C} \vec{A} \cdot d\vec{r} = 0 \implies \int^{\vec{b}}_{\vec{a}} \vec{A} \cdot d\vec{r} = f(\vec{b})-f(\vec{a})\]

이때, \(\displaystyle f(\vec{b})-f(\vec{a})=\int^{\vec{b}}_{\vec{a}}df\)이고, \(df=\nabla f \cdot d\vec{r}\)이므로 다음과 같다.

\[\displaystyle\int^{\vec{b}}_{\vec{a}} \vec{A} \cdot d\vec{r} = f(\vec{b})-f(\vec{a}) = \int^{\vec{b}}_{\vec{a}} \nabla f \cdot d\vec{r} \implies \vec{A} = \nabla f\]

1. 1->3 증명 1->2 증명에 의해 \(\vec{A}\)가 Conservative Vector Field이면 \(\vec{A} = \nabla f\), \(\nabla \times \vec{A} = \nabla \times (\nabla f)\)이고, 성분별로 보면 \(\displaystyle (\nabla \times (\nabla f))_{i}= \sum_{j,k} \epsilon_{ijk} \partial_{j} (\nabla f)_{k} = \sum_{j,k} \epsilon_{ijk} \partial_{j}\partial_{k}f\)이다. 이걸 j, k에 대해 sum해보면 모두 상쇄되어 \((\nabla \times (\nabla f))_{i}=0\)이다.

\[\therefore ~ \nabla \times \vec{A} = 0\]

1. 2->1 증명 \(\displaystyle \int^{\vec{b}}_{\vec{a}}\vec{A} \cdot d\vec{r} = \int^{\vec{b}}_{\vec{a}} \nabla f \cdot d\vec{r} = f(\vec{b})-f(\vec{a})\). if \(\vec{a} = \vec{b}\)라면 \(\displaystyle \oint \vec{A} \cdot d\vec{r} = 0\)

2. 3->1 증명 Stokes’ Theorem에 의해 \(\displaystyle\oint_{C} \vec{A} \cdot d\vec{r} = \int_{S} (\nabla \times \vec{A})\cdot d\vec{a}\)이고, \(\nabla \times \vec{A} = 0\)이므로 \(\displaystyle \oint_{C} \vec{A} \cdot d\vec{r} = 0\)이다.

\(\therefore ~ 2 \iff 1 \iff 3\)이 모두 증명되었으므로, 셋중 하나만 만족하면 모든 성질이 성립한다.

[!tip]- \(\vec{A} = \nabla f\) 성질은 물리학에서 \(\vec{F} = -\nabla U\)로 표현된다.{title} 왜 Potential Function 앞에 -을 붙일까? 기울기 벡터 \(\nabla U\)는 Scalar Field U가 가장 급격하게 증가하거나 감소하는 방향을 가리킨다. \(-\nabla U\)의 결과는 보존력 \(\vec{F}\)가 자연적으로 에너지 U가 급격하게 감소하는 방향을 가리키는 의미를 내포하기 위함이다. 물리적으로 이게 자연스럽기 때문이다.

Divergence

Divergence란 Vector Field의 발산량을 감지하는 도구다. 어떤 Vector Field에 DIvergence를 취한다는 것은, 어떤 지점 \(\vec{r}\)에서 \(\vec{A}\)가 얼마나 발산하는지를 나타내는 스칼라를 반환하는 함수를 얻어내는 것과 같다. 계산은 다음과 같이 가능하다.

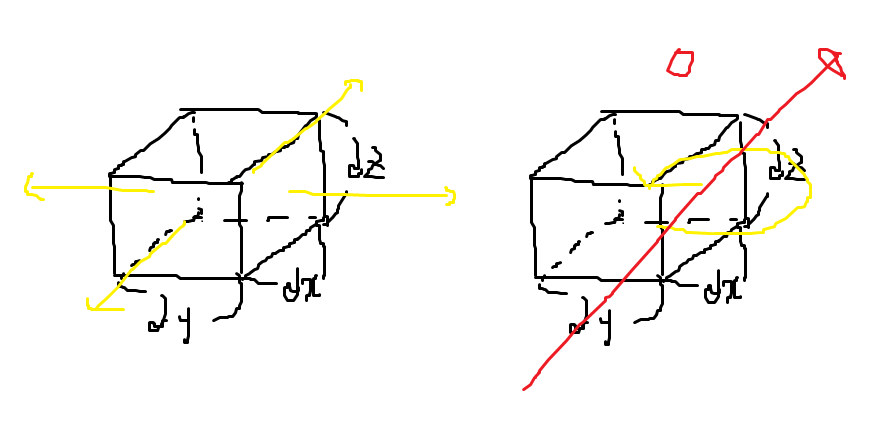
\[\nabla \cdot \vec{A}= \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right) \cdot (A_{x}, A_{y}, A_{z}) = \frac{{\partial A_{x}}}{\partial x} + \frac{{\partial A_{y}}}{\partial z} + \frac{{\partial A_z}}{\partial z}\]

Divergence는 작은 체적을 사용해서 발산을 감지해낸다. 1번의 경우 닫힌 미소 곡면에 대한 면적분 \(\displaystyle\oint_{dS} \vec{A} \cdot d\vec{s}\)가 0이 아닐 것이다. 오른쪽과 같이 회전 성분이 있다면, 안쪽에서 나와서 다시 들어가면 Flex의 총 합은 0이므로 닫힌 곡면에 대한 면적분 \(\displaystyle \oint_{dS} \vec{A} \cdot d\vec{s} = 0\)이다. \(\displaystyle \oint_{dS} \vec{A} \cdot d\vec{s} = \nabla \cdot \vec{A} dV\)와 같은 관계가 있으므로, \(\nabla \cdot \vec{A}\)가 \(\vec{A}\)의 발산 성분을 감지해낼 수 있는 것이다.

Gauss’ Theorem

\[\therefore ~ \iint_{\partial V} \vec{A} \cdot d \vec{s} = \int_{V} \nabla \cdot \vec{A} dV\]

체적 내부의 Field가 발산하는 양을 모두 총 합한 것은, 닫힌 곡면 \(\partial V\)를 뚫고 나가는 Flux의 총 량과 같다는 당연한 사실을 수식이 정확히 나타내주고 있다. 무수히 많은 수도꼭지가 발산하는 물의 총 량은, 경계면을 통해 빠져나가는 물의 양과 동일하다.

[!tip]- 증명{title}

\(\vec{r}\) 위치를 중심으로 감싸는 미소 체적 V를 생각해보자. \(\displaystyle \oint_{\partial V} \vec{A} \cdot d\vec{s}\)는 각각 yz, zx, xy 평면에 평행한 두 면의 Flux와 같다.

\[\oint_{\partial V} \vec{A} \cdot d\vec{s}= \Phi_{yz} + \Phi_{zx} + \Phi_{xy}\] \[\Phi_{yz} = \iint \vec{A} \cdot (dydz \hat{x}) \mid_{x'=x+\frac{dx}{2}} + \iint \vec{A} \cdot (-dydz \hat{x})\mid_{x' = x - \frac{dx}{2}}\] \[= \iint A_{x}\left( x + \frac{dx}{2}, y', z' \right) - A_{x}\left( x-\frac{dx}{2},y',z' \right) dy'dz'\]

\(f(x,y,z)\)를 테일러 전개하면 \(\displaystyle f(x,y,z) = f(x_{0},y_{0},z_{0})+(d\vec{r} \cdot \nabla)f(\vec{r})\mid_{\vec{r}=\vec{r}_{0}}+\frac{1}{2!}\dots\) 이므로

\[f\left( x+\frac{dx}{2},y,z \right) = f(\vec{r}_{0}) + (\frac{dx}{2} \frac{\partial}{\partial x}) f(\vec{r})\mid_{\vec{r}=\vec{r}_{0}}+ \dots\] \[f\left( x-\frac{dx}{2},y,z \right) = f(\vec{r}_{0}) + (-\frac{dx}{2} \frac{\partial}{\partial x}) f(\vec{r})\mid_{\vec{r}=\vec{r}_{0}}+ \dots\] \[\displaystyle f\left( x+\frac{dx}{2},y,z \right)-f\left( x-\frac{dx}{2},y,z \right) \simeq \left( dx \frac{\partial}{\partial x} \right)f(\vec{r})\mid_{\vec{r}=\vec{r}_{0}}\]

와 같다.

\[\Phi_{yz} = \int^{z+\frac{dz}{2}}_{z-\frac{dz}{2}} \int^{y+\frac{dy}{2}}_{y-\frac{dy}{2}} \frac{{\partial A_{x}(x,y',z')}}{\partial x} dx dy'dz'\] \[\int^{x+\frac{dx}{2}}_{x-\frac{dx}{2}} f(x)dx = F\left( x+\frac{dx}{2} \right) - F\left( x-\frac{dx}{2} \right) = dx \frac{\partial}{\partial x}F(x) = f(x)dx\]

이므로,

\[\Phi_{yz} = \frac{\partial A_{x}}{\partial x}dxdydz\]

와 같다. 이를 zx, xy 평면에도 똑같이 적용 가능하므로..

\[\therefore ~ \iint_{\partial V} \vec{A} \cdot d\vec{s} = \left( \frac{{\partial A_{x}}}{\partial x} + \frac{{\partial A_{y}}}{\partial y} + \frac{{\partial A_{z}}}{\partial z} \right)dxdydz = (\nabla \cdot \vec{A})dV\]

위 식이 성립한다.

임의의 체적 \(V\)에 대한 체적 적분은 미소 체적 \(V_{i}\)를 계산해서 모두 더하여 계산할 수 있다.

\[\iint_{\partial V_{i}} \vec{A} \cdot d\vec{s}_{i} = (\nabla \cdot \vec{A})dV_{i} \implies \sum_{i} \iint_{\partial V_{i}} \vec{A} \cdot d\vec{s}_{i} = \sum_{i}(\nabla \cdot \vec{A}) dV_{i}\]

이때, 미소 체적의 면적분 값을 더하는 과정에서 겹치는 면의 Flux 양은 상쇄되어 최종적으로 Boundry 면적의 Flux값만 남게된다.

\[\therefore ~ \iint_{\partial V} \vec{A} \cdot d \vec{s} = \int_{V} \nabla \cdot \vec{A} dV\]

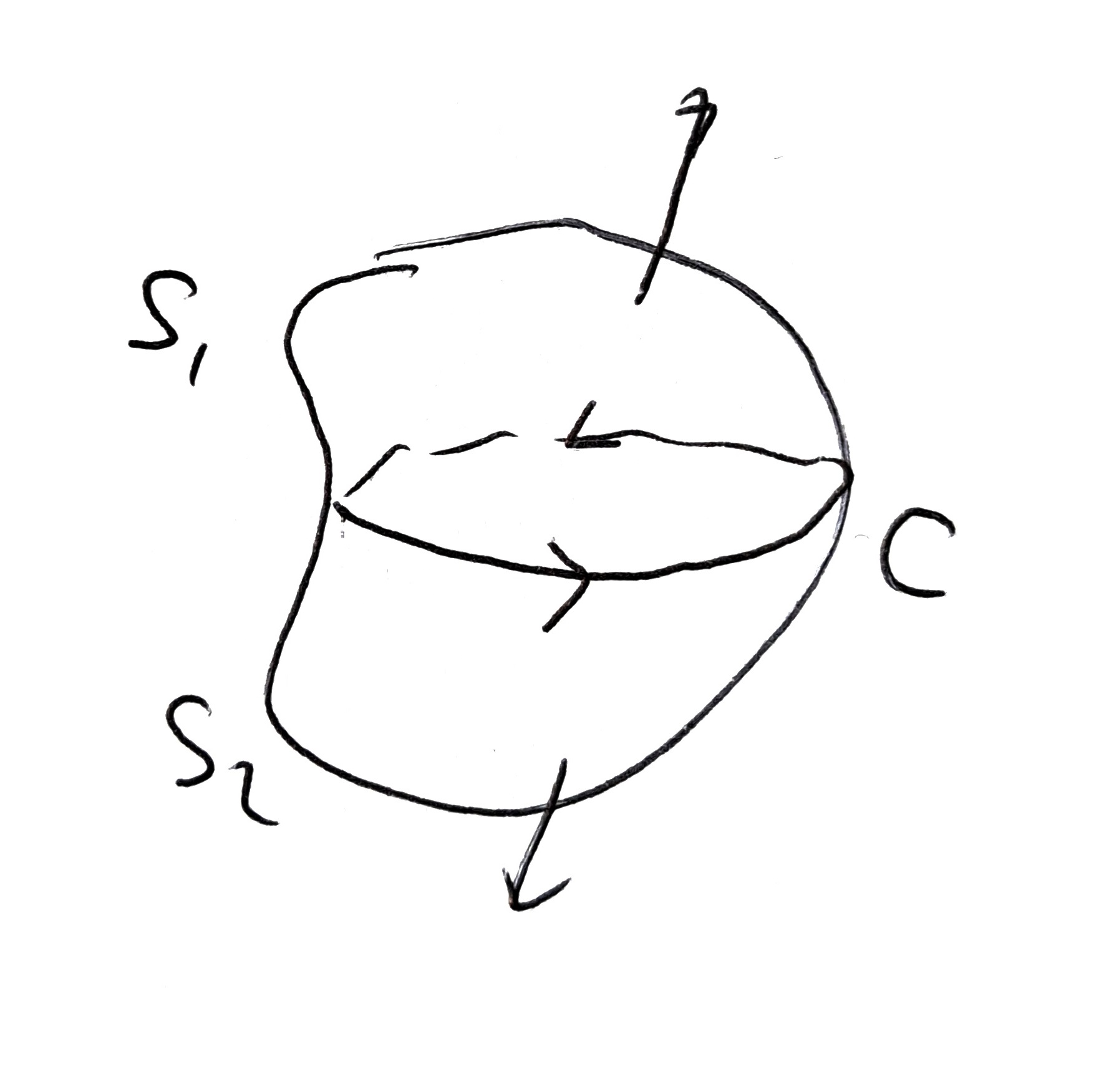
\(\nabla \cdot \nabla \times \vec{A} = 0\)인 이유

1)

\[\nabla \cdot (\nabla \times \vec{A}) =\sum_i \partial_i (\nabla \times \vec{A})_i= \sum_i \partial_i \epsilon_{ijk} \partial_j A_k= \sum_{i,j,k} \epsilon_{ijk} \partial_i \partial_j A_k\] \[= \partial_1 \partial_2 - \partial_2 \partial_1 + \partial_2 \partial_3 - \partial_3 \partial_2 +\partial_3 \partial_1 - \partial_1 \partial_3 = 0\]

2)

\[\int_S (\nabla \times \vec{A}) \cdot d\vec{S} = \int_{S_1} (\nabla \times \vec{A}) \cdot d\vec{S} + \int_{S_2} (\nabla \times \vec{A}) \cdot d\vec{S}= \oint_C \vec{A} \cdot d\vec{l} - \oint_C \vec{A} \cdot d\vec{l} = 0\] \[\int_S (\nabla \times \vec{A}) \cdot d\vec{S} = \int_V \nabla \cdot (\nabla \times \vec{A}) \, dV\] \[\therefore~ \nabla \cdot (\nabla \times \vec{A}) = 0\]