수리물리학 4. Multivariable calculus

Mathematical Methods in the Physical Sciences, Mary L. Boas의 4장 내용입니다.

Continity

1변수 함수의 연속성은 \(\displaystyle \lim_{ x \to x_{0} } f(x) = f(x_{0})\)을 만족하면 \(x=x_{0}\)에서 연속이다. 2변수 함수 이상의 연속은 \(\displaystyle \lim_{ x \to x_{0} } \lim_{ y \to y_{0} } f(x,y) = \lim_{ y \to y_{0} } \lim_{ x \to x_{0} } f(x,y) = f(x_{0},y_0)\)일 때 점 \((x_{0},y_{0})\)에서 함수 \(f(x,y)\)가 연속이라고 말할 수 있다. 반대로 생각하면, 연속 함수인 경우 \(\lim\)의 순서는 상관이 없다.

Partial Derivative

편미분의 정의는 다음과 같다.

\[\frac{{\partial f(x,y)}}{\partial x} = \lim_{ \Delta x \to 0 } \frac{{ f(x+\Delta x, y) - f(x,y) }}{\Delta x}\]

표기의 편의성을 위해 편미분 기호는 \(\displaystyle \frac{{\partial f}}{\partial x} = \partial_{x}f\)로 쓸 수 있다고 약속하자. 연속함수의 경우 미분의 순서는 상관이 없다.

\[\partial_{x} \partial_yf = \partial_{y} \partial_{x} f\]

Taylor Series

1변수 함수의 테일러 전개는 다음과 같다.

\[f(x) = f(x_0) + f'(x_0)\Delta x + \frac{1}{2!}f''(x_0)\Delta x^2 + \frac{1}{3!}f'''(x_0)\Delta x^3 + ... = f(x_{0} + \Delta x)\]

만약 2변수 함수 이상 \(f(x,y)\)를 테일러 전개하려면 어떻게 해야할까? 아이디어는 \(x=x_{0}+\Delta x\), \(y=y_{0}+\Delta y\)꼴로 쓰고 하나씩 테일러 전개를 하는 것이다.

\[f(x,y) = f(x_0 + \Delta x, y_0 + \Delta y)\] \[\displaystyle f(x,y) = f(x_0, y_0 + \Delta y) + \partial_x f(x_0, y_0 + \Delta y)\Delta x + \frac{1}{2!}\partial_x\partial_x f(x_0, y_0 + \Delta y)\Delta x^2 + ...\]

\(f(x_0, y_0 + \Delta y)\)를 따로 전개해서, 위 식에 대입하면 된다.

\[\displaystyle f(x_0, y_0 + \Delta y) = f(x_0, y_0) + \partial_y f(x_0, y_0)\Delta y + \frac{1}{2!}\partial_y\partial_y f(x_0, y_0)\Delta y^2 + \frac{1}{3!}\partial_y\partial_y\partial_y f(x_0, y_0)\Delta y^3 + ...\] \[f(x,y) = f(x_0, y_0) + \partial_y f(x_0, y_0)\Delta y + \frac{1}{2!}\partial_y\partial_y f(x_0, y_0)\Delta y^2 + \frac{1}{3!}\partial_y\partial_y\partial_y f(x_0, y_0)\Delta y^3 + \dots\]

\(\displaystyle + \partial_x f(x_0,y_0)\Delta x + \partial_x\partial_y f(x_0, y_0)\Delta x\Delta y + \frac{1}{2!}\partial_x\partial_y\partial_y f(x_0,y_0)\Delta x\Delta y^2 + ...\) \(\displaystyle + \frac{1}{2!}\partial_x\partial_x f(x_0, y_0)\Delta x^2 + \frac{1}{2!}\partial_x\partial_x\partial_y f(x_0, y_0)\Delta x^2\Delta y + ...\)

\[\displaystyle + \frac{1}{3!}\partial_x\partial_x\partial_x f(x_0, y_0)\Delta x^3 + O(\Delta^4)\]

즉, 다음과 같은 결론을 얻을 수 있다.

\[\therefore f(x,y) = f(x_0, y_0) + \left(\frac{\partial}{\partial x}\Delta x + \frac{\partial}{\partial y}\Delta y\right)f\mid_{(x_0,y_0)} + \frac{1}{2!}\left(\frac{\partial}{\partial x}\Delta x + \frac{\partial}{\partial y}\Delta y\right)^2f\mid_{(x_0,y_0)} + \dots\]

Stationary Point

함수의 값이 증가하거나 감소하지 않고 일시적으로 멈추는 점을 Stationary Point (정지점) 이라고 한다. 왜 정지점을 찾아야 하는가? 시스템의 안정점, 균형점을 찾는게 정지점을 찾는 문제와 같다. 비용 최소화, 이익 최대화 등의 최적화 문제를 푸는데도 극값을 찾아야 하므로 정지점을 찾는 문제와 똑같다.

정지점을 찾는 아이디어는 무엇인가? \(\Delta x\)이 아주 작을 때 함수의 변화율 \(\Delta f\)이 0인 지점을 찾는다. 즉, \(\Delta x \to 0 =dx\)일 때 \(df=0\)인 지점을 찾으면 된다. \(f(x)\)는 \(f(x_{0})+f'(x_{0}) \Delta x + \dots\)로 테일러 근사 가능하고, 이를 사용하면 모든 함수의 변화량 \(\Delta f\)를 명시할 수 있다. 예를 들어, 1변수 함수의 경우 다음과 같다.

\[\Delta f(x) = f(x_{0}+\Delta x)-f(x_{0})=f(x)-f(x_{0})=f'(x_{0})\Delta x+f''(x_{0})\Delta x^2+\dots\]

\(\Delta x\to 0\)인 경우 \(df(x) = f'(x_{0})dx = 0\)인 지점, \(f'(x_{0})=0\)인 \(x=x_{0}\)가 바로 정지점이 되는 위치다. 2변수 함수 이상의 경우도 똑같다.

\[f(x,y)=f(x_{0},y_{0})+\left( \frac{{\partial }}{\partial x} \Delta x + \frac{\partial}{\partial y} \Delta y\right)f\mid_{(x_{0},y_{0})} + \dots\]

와 같이 근사 가능하므로,

\[\Delta f(x,y)=f(x,y)-f(x_{0},y_{0})=\left( \frac{{\partial }}{\partial x} \Delta x + \frac{\partial}{\partial y} \Delta y\right)f\mid_{(x_{0},y_{0})}+\frac{1}{2!}\left( \frac{{\partial }}{\partial x} \Delta x + \frac{\partial}{\partial y} \Delta y\right)^2f\mid_{(x_{0},y_{0})}+\dots\]

와 같다. 정지점은, \(df(x,y)=0 \implies f_{x}(x_{0},y_{0})dx + f_{y}(x_{0},y_{0})dy = 0\)인 지점을 찾으면 된다.

\(x,y\)에 대한 구속 조건이 주어지지 않는 경우 \(x,y\)는 독립적으로 움직일 수 있다. 이런 경우는 \(f_{x}=0, f_{y}=0\)어야 식이 성립한다. \(x, y\)에 대한 구속조건이 \(x^2+y^2=4\)와 같이 주어지는 경우는 어떻게 하는가? 이런 경우, x 값이 결정되면 자동으로 y 값이 결정되는, 변수가 서로 의존 관계이다. 구속 조건을 음함수 꼴 \(g(x,y)=0\)로 바꾸고, \(dx, dy\)를 추출해야 한다. \(dg(x,y)=g_{x}dx+g_{y}dy=0\), \(g(x,y)\)는 항상 0이기 때문에 \(dg\)도 0이다. 따라서, \(\displaystyle dy=-\frac{g_{x}}{g_{y}}dx\)이고, 대입하면 \(\displaystyle f_{x}dx - f_{y} \frac{g_{x}}{g_{y}} dx=0 \implies \frac{f_{x}}{f_{y}}=\frac{g_{x}}{g_{y}}\) 식을 풀면 끝이다. 매번 이 과정을 생각하기 귀찮기 때문에, 이를 일반화한 과정이 존재한다. 그 과정이 Lagrange multiplier method이다.

Lagrange multiplier method

\(g(x,y)=0\)과 같이 조건이 주어질 때, \(f(x,y)\)의 Stationary Point를 찾는 방법이다. 먼저, 함수를 하나 새로 정의한다.

\[F(x,y,\lambda)=f(x,y)-\lambda g(x,y)\]

이때 도구로서 사용하는 \(\lambda\)가 Largange multiplier이다. 이때 \(F\) 함수의 Stationary Point를 찾으면 그 Point가 원래 함수 \(f(x,y)\)의 Stationary Point와 같다. 만약 구속 조건이 \(g_{1}(x,y,z)=0, g_{2}(x,y,z)=0\) 이렇게 여러개면, \(F(x,y,z,\lambda_{1},\lambda_{2})=f(x,y,z)-\lambda_{1}g_{1}(x,y,z)-\lambda_{2}g_{2}(x,y,z)\) Largange multiplier를 추가하면 된다.

실제로 해보면, \(dF(x,y,\lambda)=F_{x}dx + F_{y}dy + F_{\lambda}d\lambda=0\)이고, \(x,y,\lambda\)는 모두 독립 변수이므로 \(F_{x}=0, F_{y}=0, F_{\lambda}=0\)일 때 \((x,y)\) 값을 찾으면 된다. \(F_{x}=f_{x}-\lambda g_{x}\), \(F_{y}=f_{y}-\lambda g_{y}\), \(F_{\lambda}=-g(x,y)=0\). \(\lambda\)에 대한 F 미분으로 자동으로 구속조건이 나오고, \(F_{x}=0, F_{y}=0\) 식을 연립하면 자동으로 아까 찾은 식인 \(\displaystyle \frac{f_{x}}{f_{y}}=\frac{g_{x}}{g_{y}}\)가 튀어 나오도록 설계해둔 것이다.

Local Minimum, Maximum, Saddle Point

Stationary Point를 찾고 나면, 그 점이 Local Minimum인지 Maximum인지 Saddle Point인지 아직까지 알지 못한다. 확인하는 방법은, \(\Delta f\)의 High Order 항의 값이 양수인지, 음수인지, 0인지 비교해보면 된다.

예를들어, \((x_{0})\) Point가 \(f(x)\)의 Stationary Point라면, 그 점이 어떤 점인지 알기 위해 더 넓은 범위의 \(\Delta x\)를 살펴보는 것이다. \(\Delta f = f''(x_{0})\Delta x^2 + \dots\)이고, \(f''(x_{0})>0\)이면 \(\Delta f>0\)이므로 함수의 변화량이 증가한다? 이는 Local Minimum이다. \(\Delta f<0\)인 경우 Local Maximum이다. 만약 0이면, 더 High Order의 항\((\Delta x^3)\)의 거동을 살펴봐야 한다. 실제 그래프는 아주 작은 범위와 살짝 작은 범위가 flat한 그래프를 상상해볼 수 있다.

똑같이, \((x_{0},y_{0})\) Point가 \(f(x,y)\)의 Stationary Point라고 해보자. 더 넓은 범위의 \(\Delta x\)에서 \(\Delta f\)의 부호를 살펴보면 된다.

\[\Delta f = \frac{1}{2!}\left( \frac{\partial}{\partial x} \Delta x + \frac{\partial}{\partial y} \Delta y \right)^2f\mid_{x_{0},y_{0}}=\frac{1}{2}f_{xx}\Delta x^2 + f_{xy}\Delta x \Delta y + \frac{1}{2} f_{yy}\Delta y^2\]

\(\Delta f\)의 부호를 판별하기 위한 아이디어는, 앞의 두 항을 \(\displaystyle \frac{1}{2}f_{x x}\)로 묶어서 완전제곱꼴을 만들면, 경우의 수가 4가지로 줄어든다. 4가지를 판별식처럼 따져보면 어떤 점인지 체크할 수 있다.

\[\Delta f = \frac{1}{2} f_{xx} \Delta x^2 + f_{xy} \Delta x \Delta y + \frac{1}{2} f_{yy} \Delta y^2\] \[= \frac{1}{2} f_{xx} \left( \Delta x^2 + 2 \frac{f_{xy}}{f_{xx}} \Delta x \Delta y + \frac{f_{xy}^2}{f_{xx}^2} \Delta y^2 \right) - \frac{1}{2} \frac{f_{xy}^2}{f_{xx}} \Delta y^2 + \frac{1}{2} f_{yy} \Delta y^2\] \[= \frac{1}{2} f_{xx} \left( \Delta x + \frac{f_{xy}}{f_{xx}} \Delta y \right)^2 + \frac{1}{2} \left( f_{yy} - \frac{f_{xy}^2}{f_{xx}} \right) \Delta y^2\]

완전제곱꼴은 항상 \(>0\)이다. \(A=f_{xx},~ ~B=f_{xy}, ~C=f_{yy}\)라고 하면 \(A\)와 \(\displaystyle C-\frac{B^2}{A}\)의 부호만 비교하면 된다.

1. \(\displaystyle A>0~~ \cap~~ C-\frac{B^2}{A} > 0\) : \(\Delta f>0\), Local minimum
2. \(\displaystyle A<0~~ \cap~~ C-\frac{B^2}{A} < 0\) : \(\Delta f<0\), Local maximum
3. \(\displaystyle A \cdot (C-\frac{B^2}{A}) < 0\) : \(\Delta f\)가 양수일 수도, 음수일 수도 있음. 따라서 Saddle Point
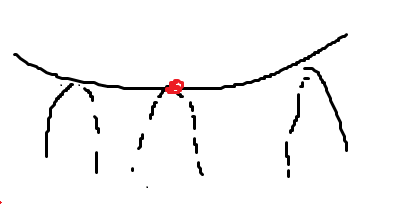
4. 만약 \(f_{xy}=0\)인 경우는 훨씬 편하다. \(\displaystyle \Delta f=\frac{1}{2}f_{x x}\Delta x^2 + \frac{1}{2}f_{yy}\Delta y^2\)이므로 \(f_{ x x}\), \(f_{ y y}\)의 부호만 비교해주면 된다. \(f_{ x x} \cdot f_{ yy} < 0\)인 경우 아래 그림과 같은 Saddle Point이다.

Multiple integral

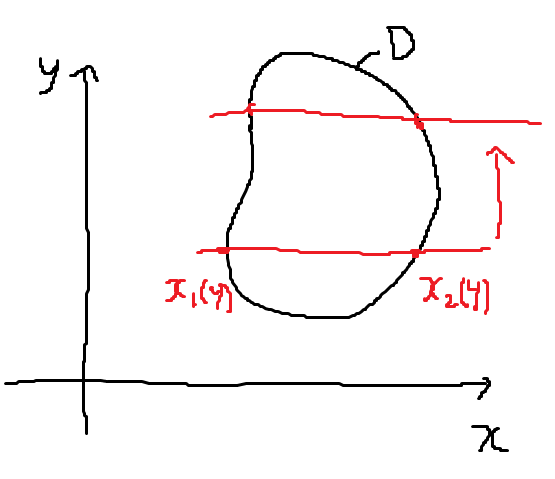
임의의 도메인 D에 대해 다변수 함수 \(f(x,y)\)를 적분하는 것은 \(\displaystyle \iint_{D} f(x,y)dxdy\)와 같고, 이를 도메인을 입력으로 받는 함수 \(F(D)\)로 생각할 수 있다.

이론적으로, Multiple integral는 변수 하나를 고정시켜 다른 하나를 먼저 적분하는 방법으로 계산할 수 있다. 예를 들어, y를 고정시키고 x부터 적분하면 \(\displaystyle \int f(x,y)dx\)다. 적분 범위는, y가 변함에 따라 달라지므로 y에 대한 함수가 적분 범위어야 한다. \(\displaystyle \int^{x_{2}(y)}_{x_{1}(y)}f(x,y)dx\), y의 최대 최소 범위는 상수값이므로 \(\displaystyle F(D)=\int^{y_{2}}_{y_{1}}\int^{x_{1}(y)}_{x_{2}(y)}f(x,y)dxdy\)로 기술된다. 일반적으로 이 적분 범위를 찾는 것이 매우 어려워, 좌표 변환을 통해 적분 구간을 간단히 하고자 하는 시도가 많다.

좌표 변환을 하면, 변환 함수의 자코비안을 찾아 Scaling Factor로 \(dA\)에 곱해주거나, 직접 각 축에 대한 Scale Factor \(h_{1}, h_{2}, \dots\)를 찾아서 곱해도 된다. 예를 들어, 구면 좌표계에선 xy평면에서 돌아가는 각을 \(\phi\), rz평면에서 돌아가는 각을 \(\theta\)로 정의한다. 변환 함수 \((x,y,z)=\vec{T}(r,\theta,\phi)=(r\sin \theta \cos \phi,r\sin \theta \sin \phi,r\cos \theta)\)의 자코비안은 \(r^2\sin \theta\)이며, 각각 축의 Scaling Factor는 \(h_{r}=1\), \(h_{\theta}=r\), \(h_{\theta}=r\sin \theta\)이다. 직관적으로 각 축의 Scaling Factor를 찾을 수 있다면, 찾으면 되고 복잡한 변환이라면 자코비안을 찾으면 된다.

Gaussian Integral

가우시안 분포 함수 \(\displaystyle I(\alpha)= \int_{-\infty}^{\infty} e^{-\alpha x^2} dx\)는 그냥 적분하기 힘드므로, 제곱하여 Multiple Intergral로 바꾸고, 좌표 변환을 통해 적분 가능한 함수 모양으로 바꾸는 트릭을 사용한다. \(\displaystyle I^2(\alpha)=\int_{-\infty}^{\infty} e^{-\alpha x^2}dx\int_{-\infty}^{\infty} e^{-\alpha y^2}dy\), 적분 구간이 서로 독립적이므로 합치면 \(\displaystyle =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} e^{-\alpha (x^2+y^2)}dxdy\)이고, \(x^2+y^2\) 꼴이 나왔으므로 극좌표계로 변환하면 좋을 것 같다. 이때, 도메인이 \(\mathbb{R}^2\)일 때 극좌표계의 적분 범위는 \(r=[0,\infty]\), \(\theta=[0,2\pi]\)로 잡아도 충분하다.

\[\int_{0}^{\infty} \int_{0}^{2\pi} r e^{-\alpha r^2} dr \theta=\sqrt{ \frac{\pi}{\alpha} }\]

미소 입체각

구면좌표계의 체적소는 \(dV = r^2 dr \sin \theta d\theta d\phi = r^2 dr d \Omega\) \(d\Omega\)는 단위 구에서의 미소 입체각(solid angle)라고 정의한다. \(\displaystyle \frac{dA}{r^2} = d\Omega =\sin \theta d\theta d\phi\), 즉 길이 요소를 뺀 순수 각도 요소만 합친 것이다.