수리물리학 3. 선형대수

Mathematical Methods in the Physical Sciences, Mary L. Boas의 3장 내용입니다.

좌표계의 변환은 행렬이다?

같은 벡터지만 좌표계에 따라 다른 성분을 가질 수 있다. 기저가 다르면 그 성분또한 달라지기에 당연하다. \(\displaystyle \vec{A} = \sum_{i} A_{i} \hat{e}_{i} = \sum_{i} A_{i}' \hat{e}_{i}'\), 우리가 알고싶은 것은, \(A_{i}, \hat{e}_{i}, \hat{e}_{i}'\)를 알고있을 때 다른 좌표계의 성분, 즉 \(A_{i}'\)를 구할 수 있느냐가 궁금한 점이다.

행렬의 대수구조

행렬이란, 단순히 숫자들을 \(m \times n\) 크기의 박스 안에 나열한 것이라고 볼 수 있다. 숫자를 1차원에 나열한 것을 벡터, 3차원 이상에 나열한 것은 텐서라고 부른다. 이러한 수학적 대상을 다루기 위해서 여러가지 연산자들을 정의할 수 있다. 연산자들을 잘 정의하고 나면, 그 대수구조가 어떤 대수구조와 일치하는지 파악하면 행렬을 다루기 수월해질 것이다.

먼저, 플러스 연산(\(+\))을 정의한다. 더하기 연산은 단순히 두 행렬의 같은 위치의 원소를 합하는 것으로 생각할 수 있다. \((M + N)_{ij} = M_{ij} + N_{ij}\). 두 행렬의 크기가 다르면, 더하기 자체를 정의하지 않겠다. 이렇게 정의하면 그저 여러개의 스칼라를 더하는 것과 같으므로 역원과 항등원이 정의되고, 교환법칙과 결합법칙이 성립된다.

이후, 스칼라 곱(\(\cdot\))를 정의하자. 이 또한 단순히 각 원소에 스칼라를 곱하는 것으로 정의할 수 있다. \((cM)_{ij}=cM_{ij}\). 이때 스칼라 곱과 플러스 연산이 분배법칙을 만족하면, 같은 크기의 행렬을 집합으로 갖는 대수구조는 벡터 공간을 만족하는 것과 같다. 정말 분배법칙을 만족할까?

\[(c(M+N))_{ij}=c(M+N)_{ij}=c(M_{ij}+N_{ij})=cM_{ij}+cN_{ij}\]

분배 법칙을 만족하네. 따라서 같은 크기의 행렬을 집합으로 갖는 대수구조는 일단 벡터 공간을 만족하고 벡터의 성질을 따를 수 있다.

그렇다면, 행렬과 행렬을 곱하는 곱연산은 어떻게 정의할 수 있을까? 정의 방식이 좀 특이하다고 생각할 수 있다. 크기가 \(p\times q\)인 행렬 \(M\)과 크기가 \(q\times r\)인 행렬 \(N\)의 곱은 다음과 같다.

\[(MN)_{ij}=\sum_{k=1}^q M_{ik} N_{kj}\]

두 행렬의 크기 사이의 값이 같아야 곱연산을 할 수 있고, 그렇지 않은 경우는 곱셈을 정의하지 않는다. 왜 이렇게 정의하는가? 행렬은 단순히 숫자들의 모임이지만, 여러가지 해석하는 방법이 존재한다. 그중 대표적으로 좌표계 변환, 선형 변환 등이 있는데 연속적인 변환을 행렬 곱으로 해석하려면 저렇게 정의하는게 자연스럽다.

Determiant

역행렬의 정의는, \(MM^{-1}=\mathbb{1}\)을 만족하는 행렬 \(M^{-1}\)이다. \(M = \begin{bmatrix}a&b \\ c&d\\ \end{bmatrix}\) 행렬부터 살펴보면, 역행렬을 \(M^{-1} = \begin{bmatrix}x&y \\ z&w\\ \end{bmatrix}\)라고 했을 때 \(MM^{-1} = \begin{bmatrix}a&b \\ c&d\\ \end{bmatrix}\begin{bmatrix}x&y \\ z&w\\ \end{bmatrix} = \begin{bmatrix}1&0 \\ 0&1\\ \end{bmatrix}\)를 만족해야 한다. 이를 풀어쓰면 다음과 같다.

\[\begin{bmatrix} ax + bz & ay + bw \\ cx + dz & cy + dw \end{bmatrix} = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \implies \begin{cases} ax+bz = 1 \\ cx + dz = 0 \\ ay + bw = 0 \\ cy + dw = 1 \end{cases}\]

1, 2번 식에 각각 z가 지워져 x만 살아남도록 방정식 하나와 x가 지워져 z만 살아남도록 연립방정식을 만들면 \((ad - bc)x = d\), \((bc - ad)z = c\)이다. 똑같이 3, 4번식을 재연립하면 \((ad - bc)y = -b\), \((bc - ad)w = -a\)이므로 \(\displaystyle M^{-1} = \frac{1}{ad-bc} \begin{bmatrix} d & -b \\ -c & a \\ \end{bmatrix}\)와 같이 적을 수 있다. \(ad-bc\) 값이 0이냐 0이 아니냐에 따라 역행렬이 존재할 수도, 존재하지 않을 수도 있다. 이를 Determiant라고 정의하자.

Determiant는 변환 행렬 M의 Scaling Factor라고 생각할 수 있다. Determiant가 0이라는 것은, Scaling 했을 때 크기가 0이 되었다는 뜻이다. 그러한 유형의 변환은, 2차원 공간에서 1차원 선으로 차원이 축소되는 변환에 해당된다. 당연히 이런 유형의 변환은 역변환을 할 방법이 없으며, 따라서 역행렬이 존재하지 않는다. 기저가 \((1, 4)\), \((3, 12)\)와 같이 선형 종속적이라면 기저가 Spanning하는 차원이 감소해버리고, 이런 경우가 \(\det M=0\)인 경우다.

[!example] Det M = 0인 경우의 연립방정식{title}

\[\begin{bmatrix} 1 & 3 \\ 4 & 12 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\implies \begin{cases} x + 3y = 1 \\ 4x + 12y = 2 \end{cases}\]

위의 경우, 해가 존재하지 않는다.

\[\begin{bmatrix} 1 & 3 \\ 4 & 12 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 1 \\ 4 \end{bmatrix} \implies \begin{cases} x + 3y = 1 \\ 4x + 12y = 4 \end{cases}\]

위의 경우, 똑같은 식이다. 따라서 해가 무한히 많다.

Determiant 구하는 식도 일반화 해보면 다음과 같다.

\[\displaystyle \det M_{2 \times 2} = \sum_{i, j=1}^2 \epsilon_{ij} M_{1i} M_{2j}\]

\(\displaystyle \det M_{3 \times 3} = \sum_{i,j,k=1}^3 \epsilon_{ijk} M_{1i} M_{2j} M_{3k}\) 왜? Determiant 식의 규칙을 잘 살펴보니, \(M_{1i}M_{2j}M_{3k}\)에서 행 넘버는 고정해두고 열 넘버를 겹치지 않게 하나씩 뽑는 것과 같다. 이는 \((1,2,3)\)의 순열이고, Swap 횟수가 홀수면 마이너스가 붙는다는 규칙을 발견했기 때문이다. \(\det M_{3 \times 3} = M_{11} M_{22} M_{33} - M_{12} M_{21} M_{33} + M_{12}M_{23}M_{31} - M_{13}M_{22}M_{31}-\dots\) 따라서 중복을 허용하지 않고 세 자리에서 하나씩 뽑는 것과 같으므로 경우의 수는 \(3 \times 2 \times 1 = 6\)가지. 따라서 \(3 \times 3\) 행렬의 행렬식 항은 6가지가 존재한다. \(4 \times 4\)행렬의 행렬식은 \(4 \times 3 \times 2 \times 1 = 24\)개 항이 존재할 것이다.

Properties of Determinants

• \(i\neq j \neq k\)일 때 다음과 같다.

\[\displaystyle \sum_{l,m,n} \epsilon_{lmn} M_{il} M_{jm} M_{kn} = \epsilon_{ijk} \det M\]

\(i, j, k = 1,2,3\)이면 \(\det M\), \(i, j, k= 2, 1, 3\)이면 \(-\det M\)

• 한 열에 곱해진 상수는 밖으로 뺄 수 있다.

\[\det \begin{pmatrix}a M_{11}& aM_{12} & aM_{13} \\ M_{21} & M_{22} & M_{23} \\ M_{31} & M_{32} & M_{33} \end{pmatrix} = a \det M\]

a는 한번씩만 뽑히기 때문이다. 똑같은 논래로, a가 한 열에 곱해져도 한번씩 밖에 안뽑히므로 \(\displaystyle \det \begin{pmatrix}a M_{11}& M_{12} & M_{13} \\ aM_{21}&M_{22} & M_{23} \\ aM_{31} & M_{32} & M_{33} \end{pmatrix} = a \det M\) 또한 성립한다.

• 한 열, 또는 한 행이 모두 0이면 그 행렬의 Determiant는 항상 0이다.

\[\det \begin{pmatrix}0& 0 & 0 \\ M_{21}&M_{22} & M_{23} \\ M_{31} & M_{32} & M_{33} \end{pmatrix} = 0\]

한 행 또는 한 열이 0이면 무조건 0이 한번 곱해지기 때문에 0이라고 생각해도 되고, 3차원이 2차원으로 축소하는 변환을 생각해보면 그 Size Factor는 직관적으로 0이다.

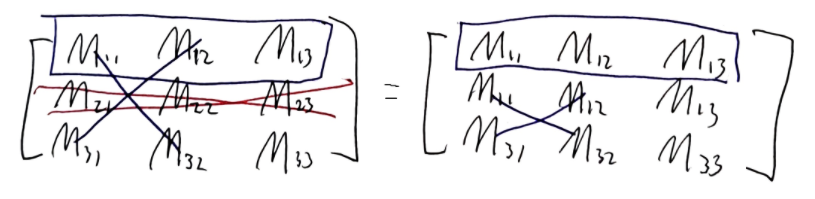
• 행렬 \(M\)에서 Two Rows or Columns를 교환하면 -가 붙는다.
  • \(M\) 행렬에서 두 행을 바꾼 행렬을 \(\displaystyle M' = \begin{pmatrix}M_{21}&M_{22} & M_{23} \\ M_{11}& M_{12} & M_{13} \\ M_{31} & M_{32} & M_{33} \end{pmatrix}\)라고 할 때 다음과 같음.

\[\det M' = \sum_{i, j, k} \epsilon_{ijk} M_{2i} M_{1j} M_{3k} = \sum_{i, j, k} -\epsilon_{jik} M_{1j} M_{2i} M_{3k} = -\det M\]

똑같은 논리로, 두 열을 바꿔도 동일하다.

\[\det M'' = \sum_{i, j, k} \epsilon_{ijk} M_{i 2} M_{j 1} M_{k 3} = - \sum_{i,j,k} \epsilon_{jik}M_{i 2} M_{j 1} M_{k 3} = -\det M\]

• 행렬 Column이 중복되는 경우 그 행렬의 Determiant는 0이다.

\[M= \begin{pmatrix}a&b & c \\ a& b & c \\ e &f & g \end{pmatrix}\]

예를들어 위와 같은 행렬일 가정하자. 5번 성질에 의해 두 row를 바꾸면 부호가 바뀌어야 하는데, 1열 2열을 바꿔도 똑같은 행렬이고 \(\det M = -\det M\)이 같으려면 \(\det M=0\)일 수밖에 없다. 또는 두 기저가 선형 종속적이므로 3번 케이스와 동등하다고 볼 수있음. 따라서, \(\det M=0\)이다.

• 두 행렬 \(M, N\)이 \(n \times n\)으로 같은 크기라면, \(\det(MN) = \det M \cdot \det N\)이다.

\[\det(MN) = \sum_{i,j,k} \epsilon_{ijk} (MN)_{1i} (MN)_{2j} (MN)_{3k}\]

이때 두 행렬의 곱은 \(\displaystyle (MN)_{ij} = \sum_{k=1}^n M_{ik}N_{kj}\)이므로 풀어쓰면 다음과 같다.

\[= \sum_{i,j,k} \epsilon_{ijk} \sum_{l} M_{1l}N_{li} \sum_m M_{2m}N_{mj} \sum_n M_{3n}N_{nk}\] \[= \sum_{l,m,n} \sum_{i,j,k} \epsilon_{ijk} N_{li} N_{mj} N_{nk} (M_{1l}M_{2m}M_{3n})\]

\(\displaystyle \sum_{l,m,n} \epsilon_{lmn} M_{il} M_{jm} M_{kn} = \epsilon_{ijk} \det M\)이므로 다음과 같다.

\[= \sum_{l,m,n} \epsilon_{lmn} \det N \cdot(M_{1l}M_{2m}M_{3n}) = \det M \cdot \det N\]

• 역행렬이 존재한다면, \(\det M^{-1}=\displaystyle\frac{1}{\det M}\)이다. 만약, 행렬 M의 역행렬 \(M^{-1}\)이 존재한다고 하면 \(MM^{-1}= \mathbb{1}\)을 만족한다.

\[\det (M M^{-1}) = \det \mathbb{1} \implies \det M \det M^{-1} =1 \implies \det M^{-1} = \frac{1}{ \det M}\]

선형 종속과 선형 독립

선형 종속을 명확하게 설명하는 방법은, 기저의 나머지 벡터들로 한 벡터를 만들 수 있을 때 선형 종속적이라고 한다.

선형 독립적이라는 것은 \(a \vec{u}_{1} + b \vec{u}_{2} + c \vec{u}_{3} = 0\)를 만족하는 \(a, b, c\)가 \(a= b=c=0\) 뿐일 때 선형 독립적이다. 반대로 선형 종속이면 두 벡터로 나머지 하나의 벡터를 표현할 수 있게된다.

\[a \vec{u}_{1} + b \vec{u}_{2} = - c \vec{u}_{3} \implies \vec{u}_{3} = - \frac{a}{c} \vec{u}_{1} - \frac{b}{c} \vec{u}_{2}\]

행렬식을 계산하는 방법

한 행 또는 한 열의 성분을 하나씩 뽑아내면 그 뒤에 Cofactor가 곱해진다. 예를들어, 첫번째 행을 뽑아내면 \(\det M= M_{11} cof(M_{11}) + M_{12} cof(M_{12}) + M_{13} cof(M_{13})\)이고, 두번째 열을 뽑아내면 \(\det M=M_{12}cof(M_{12}) + M_{22}cof( M_{22}) + M_{32}cof(M_{32})\)이다.

그 이유는, 행렬식 정의에서 살펴볼 수 있다.

\[\det M = \sum_{i,j,k}\epsilon_{ijk} M_{1i} M_{2j} M_{3k} = \sum_{i} M_{1i} \sum_{j,k} \epsilon_{ijk}M_{2j}M_{3k}\] \[= M_{11}\sum_{j,k} \epsilon_{1jk}M_{2j}M_{3k} + M_{12}\sum_{j,k} \epsilon_{2jk}M_{2j}M_{3k} + M_{13}\sum_{j,k} \epsilon_{3jk}M_{2j}M_{3k}\]

뒤의 항은, 각각 앞에 곱해진 행, 열 넘버를 제외한 행렬의 Determiant와 같다. 이를 Cofactor(여인수)로 정의한다.

\[cof(M_{ij})\equiv(-1)^{i+j} \det M_{ij}^C\]

위와 같은 함수를 하나 정의하면 다음과 같이 쓸 수 있다. 이때, \(M^C_{ij}\)는 i행 j열을 제외한 행렬을 의미한다.

\[\det M = M_{11} cof(M_{11}) + M_{12}cof(M_{12}) + M_{13}cof(M_{13})\]

똑같은 논리로, 다른 행을 뽑거나, 다른 열을 뽑을 수 있다.

\[\displaystyle \det M = \sum_j M_{2j}\sum_{i,k} \epsilon_{ijk}M_{1i}M_{3k}\] \[= \sum_k M_{3k}\sum_{i,j} \epsilon_{ijk}M_{1i}M_{2j}\] \[\displaystyle =\sum_{i,j,k} \epsilon_{ijk} M_{i 1} M_{j 2} M_{k 3}\] \[= \sum_{i} M_{i_{1}} \sum_{j,k} \epsilon_{ijk} M_{j 2} M_{k 3} = \dots\]

Inverse Matrix

\(M_{2\times 2}, M_{3 \times 3}, \dots\) 역행렬을 구하는 식을 일반화 하면, Determiant 역수의 곱과 어떤 행렬의 곱인 형태로 나온다는 것을 알 수 있다. 그 어떤 행렬이 무엇인지 알아보니, Cofactor Matrix의 Transpose (전치) 행렬이였다. \(\displaystyle M^{-1}=\frac{1}{\det M} (adj(M))^T\), 또는 성분으로 표기하면 \(\displaystyle M^{-1}_{ij}=\frac{1}{\det M} cof(M_{ji})\) 와 같다. Cofactor Matrix은 행렬의 각 성분이 \(cof(M_{ij})\)로 이루어진 행렬로 정의한다.

\[adj(M) \equiv \left( \begin{matrix} cofM_{11}&cofM_{12}&cofM_{13} \\ cofM_{21}&cofM_{22}&cofM_{23} \\ cofM_{31}&cofM_{32}&cofM_{33} \end{matrix}\right)\]

따라서, \(3\times 3\) 역행렬은 단순히 \(\displaystyle M^{-1}= \frac{1}{ \det M} \left( \begin{matrix} cofM_{11}&cofM_{21}&cofM_{31} \\ cofM_{12}&cofM_{22}&cofM_{32} \\ cofM_{13}&cofM_{23}&cofM_{33} \end{matrix}\right)\)를 계산하면 된다.

정말로 맞을까? 증명해보자. 편의를 위해 성분을 \((MM^{-1})_{ik}\)로 표기하겠다.

\[(MM^{-1})_{ik} = \sum_j M_{ij}M_{jk}^{-1} = \sum_j M_{ij}\left(\frac{1}{\det M}cof(M_{kj})\right) = \frac{1}{\det M}\sum_j M_{ij}cof(M_{kj})\]

Determiant는 \(\displaystyle \det M=\sum_{i}M_{1i} cof(M_{1i}) = \dots = \sum_{i} M_{ij} cof(M_{ij})\)이다. \(k=i\)인 경우 \(\displaystyle \sum_j M_{ij}cof(M_{kj})\)는 정확히 \(\det M\)과 같다. \(k\neq i\)인 경우, \(\displaystyle \sum_j M_{ij}cof(M_{kj})\)는 이렇게 생각해볼 수 있다. \(M_{1i}\)를 뽑았지만 cofactor로 \(M_{2i}\)같은 엉뚱한 행을 지우고 있는 상황이라고 생각할 수 있다.

그런 상황은 마치, 같은 행이 두번 있는 행렬의 Determiant를 구하는 상황과 동등하다. 이때의 Determiant는 0이다. 따라서 \(k=i\)인 케이스만 성분이 \(\displaystyle \frac{1}{\det M} \det M = 1\)이고, \(k \neq i\)인 경우 성분은 0이다. 따라서, \((MM^{-1})_{ik} = \delta_{ik}\)와 같고 \(MM^{-1}= \mathbb{1}\)이 증명된다.

Operations of Matrix

• Transpose : \((M^T)_{ij} = M_{ji}\)
• Adjoint or Hermitian conjugate : \((M^{\dagger})_{ij} = M_{ji}^*\) M이 Real이면, \(M^{\dagger} = M^T\)와 같다. Dagger 연산 또한 분배가 되는데, 분배시 행렬 곱의 순서가 바뀐다. \((MN)^{\dagger} = N^{\dagger} M^{\dagger}\)

\(e^M\)

\(e^M\)이 가능할까? \(e^M = 1 + M + \frac{1}{2!} M^2 + \frac{1}{3!} M^3 + \dots\)이 수렴만 하면 정의 가능. 계산 자체는 1은 I고, 전부 n by n 행렬이고 제곱 +연산 스칼라곱 다 정의된 연산이기 때문에 계산이 가능하다.

Special Matrix

• Symmetric Matrix : \(M = M^T, M_{ij}= M_{ji}\)
• Hermitian Matrix : \(M=M^{\dagger}, M_{ij}=M_{ji}^*\)
• Orthogonal Matrix : \(M^T=M^{-1}\)
• Unitray Matrix : \(M^{\dagger} = M^{-1}\)

Orthogonal 행렬 중 대표적인 행렬은 Rotation 행렬이 있다. Rotation 행렬의 역행렬은 \(\theta\) 대신 \(-\theta\)만큼 변환한 것인데, 그 결과는 행렬을 전치한 것과 같다. 다르게 생각해보면, Rotation 행렬은 방향만 변화시키고 벡터의 크기는 바뀌지 않는다. 따라서 변환 전 벡터의 크기와 변환 후 벡터의 크기가 같아야 한다.

\[\sum_{i}v_{i}^2 = \sum_{i} v_{i}'^2 = \sum_{i} v_{i}' v_{i}'\] \[= \sum_{i} \left( \sum_{j} R_{ij} v_{j} \right)\left( \sum_{k} R_{ik} v_{k}\right) = \sum_{j, k}\left( \sum_{i} R_{ij} R_{ik} \right) v_{j} v_{k}\] \[= \sum_{j, k}\left( \sum_{i} (R^T)_{ji} R_{ik} \right) v_{j} v_{k}\]

이때, R의 전치행렬과 R의 곱은 \(j\neq k\)일 때 0이어야 한다. 그렇지 않을 경우, \(v_{1}v_{2}\)와 같은 항이 존재하여 \(v_{1}^2 + v_{2}^2 + v_{3}^2\)과 등호가 성립되지 않기 때문이다. 또, \(j=k\)일 때 1이어야 한다. 이는 크로네커 델타 \(\delta _{jk}\)와 동일하다. 따라서, \(R^T R = \mathbb{1}\)을 만족하는 관계는 역행렬 관계이기 때문에, 회전 행렬은 \(R^T = R^{-1}\)인 Orthogonal Matrix이다.

Space, Coordinate System, Transformation

수학에서 공간이란, 구조적 성질을 갖는 어떤 수학적 대상이 Span하여 얻어지는 집합을 의미한다. 예를들어, 벡터 공간은 서로 선형 독립인 벡터가 Span하는 Space를 의미한다. 함수 공간은, 서로 선형 독립인 함수가 Span하는 Space를 의미한다. Span된 공간 위에 포함되는 모든 수학적 대상은 기저로 사용된 수학적 대상의 선형 조합으로 표현될 수 있다.

좌표계란, 공간 위의 수학적 대상을 해석하기 위해 도입하는 System이다. 좌표계에 따라 같은 수학적 대상이라도, 다른 방법으로 해석될 수 있다. 예를들어, 데카르트 좌표계에서 \(\vec{v}=(1, 1, 0)\)로 해석되는 벡터가 구면 좌표계에서 \(\left( 1, 0, \frac{2}{\pi} \right)\)로 해석될 수 있다.

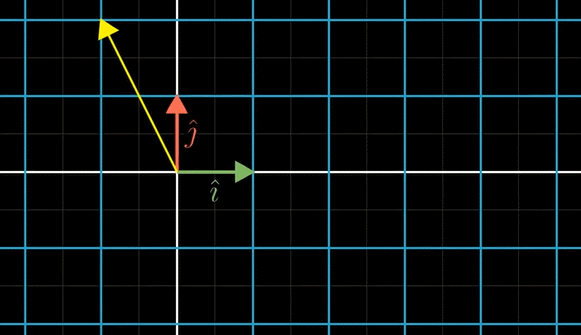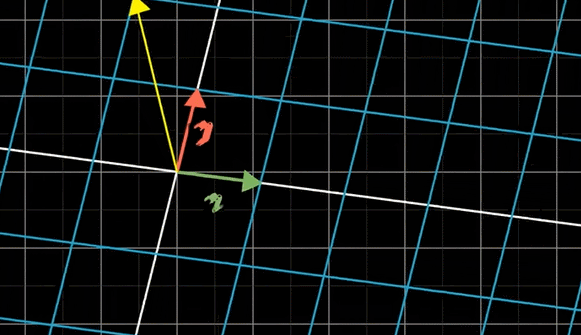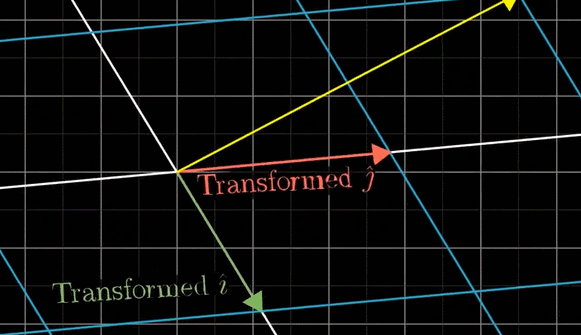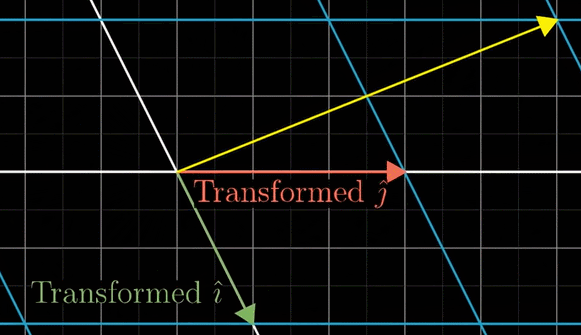
Linear Transformation, Coordinate Transformation

변환이란, 수학적 대상을 어떤 규칙을 적용하여 다른 수학적 대상으로 바꾸는 것을 의미한다. 이때 선형 변환이란, 공간의 변형을 의미한다. 다른 말로, 한 공간에서 다른 공간 위로 수학적 대상의 성분을 보존시키며 이동시키는 변환이다. 다른 공간이라는 것이 완전히 다른 수학적 대상의 집합을 의미하는 것은 아니다. 같은 수학적 대상이 Span하는 공간이지만, 공간 자체가 압축, 팽창하거나 회전하는 등의 변화는 충분히 생각해볼 수 있다. 선형 변환은 그러한 유형의 변환을 일컫는다. 두 벡터 공간 V, W가 존재하고 V -> W로 변환하는 Transformation Matrix를 M이라고 하자. V Space에서 바라본 W Space의 Basis는 각각 \((1, -2), (3, 0)\)으로 표현된다고 하자. 이때 \(M\)은 \(\left( \begin{matrix} 1 & 3\\ -2 & 0 \end{matrix} \right)\)으로 적을 수 있다. Linear Transfomation Matrix를 만드는 규칙은, 옮기고 싶은 Space의 Basis Vector을 기존의 Space에서 바라본 성분을 찾아 Column에 적으면 된다. 예를 들어, \(\vec{v} = (-1, 2)\) 벡터를 M Matrix를 사용하여 변환하면, V Space 입장에서는 벡터가 \(\left( \begin{matrix} 1 & 3\\ -2 & 0 \end{matrix} \right) \left( \begin{matrix}-1 \\ 2\end{matrix} \right) = \left( \begin{matrix}5 \\ 2\end{matrix} \right)\)로 변형된다. 하지만 이는 W Space로 \((-1, 2)\) 성분의 벡터가 그대로 옮겨간 것이며, W Space에서 벡터는 \((-1, 2)\) 성분이며 W Space 입장에서는 기저벡터 또한 \((1, 0), (0, 1)\)로 해석된다.

좌표계 변환이란, 공간은 그대로인데 Coordinate System을 바꾸는 변환이다. 똑같은 벡터라도, 좌표계에 따라 다른 성분으로 표현될 수 있다. 벡터를 그대로 유지하면서, 그 벡터가 다른 좌표계에서 어떤 성분으로 표현되는지 알고 싶을 때 좌표계 변환을 적용하면 된다. 좌표계 변환 Matrix는 선형 변환 Matrix의 역행렬이다.

Eigenvalue Problem

어떤 행렬은 벡터를 변환시키는 것으로 생각 할 수 있는데, 변환 후에도 방향은 변하지 않고 길이만 늘었다 줄었다 하는 특별한 벡터가 존재할 수 있다. 그 벡터의 방향은 변환의 축이라고 생각할 수 있다. 이런 특별하고 중요한 벡터를 eigenvector, 고유벡터라고 하며, 늘어나거나 줄어드는 정도를 eigenvalue, 고유값이라고 한다. 어떤 행렬의 고유값과 고유 벡터를 찾는 것은, 그 행렬이 도대체 무엇을 하는 행렬인지 해석하는 것과 같다. 어떤 미지의 행렬이 있을 때 고유값과 고유벡터를 찾으면 그 행렬이 무슨 의미의 행렬인지 알 수 있게 되는 것이다. 이를 식으로 표현하면 다음과 같다.

\[M \vec v = \lambda \vec v\]

\(\lambda \vec v\)는 \(\lambda \mathbb 1 \vec v\)로 써도 무방하다. 식을 정리하면 다음과 같다.

\[M \vec v - \lambda \mathbb 1 \vec v = \vec 0 \implies (M - \lambda \mathbb 1 )\vec v = \vec 0\]

이때 이 방정식을 characteristic matrix, 특성 방정식이라고 하며 \(M - \lambda \mathbb 1\) 행렬을 characteristic matrix, 특성 행렬이라 한다. 만약 특성 행렬이 역행렬이 존재한다면, 그저 우항에 특성 행렬을 넘기면 특성 방정식이 만족하게 된다. 따라서 특성행렬의 역행렬이 존재하거나 벡터 v가 0벡터인 경우 특성 방정식은 항상 만족하는 항등식이 되어버리며, 이 경우는 관심 없다. 우리는, 특성 행렬의 역행렬이 존재하지 않는 \(det (M - \lambda \mathbb 1 )= 0\) 인 경우를 따져봐야 한다. 특성 행렬의 determinant를 구하는 것은 미지수가 람다인 n차 방정식을 푸는 문제와 동등하며, n차 방정식은 복소해를 허용한다면 해의 개수는 n개임을 짐작할 수 있다. 이런 방식으로 고윳값 \(\lambda\)를 구할 수 있으며, 고유 벡터는 고유값을 특성 방정식에 대입하여 그 고유값에 대응하는 고유 벡터를 찾을 수 있다.

Eigenvalue를 찾아야 한다면 \(\det(M - \lambda \mathbb{1}) = 0\)을 쓰고 시작하라. Eigenvector는 변환 후에도 방향이 바뀌지 않는 축의 의미만 담으면 된다. 따라서 Eigenvector는 방향의 정보만 가지고 있으면 되고, 일반적으로 Normalized 해주는게 좋다.

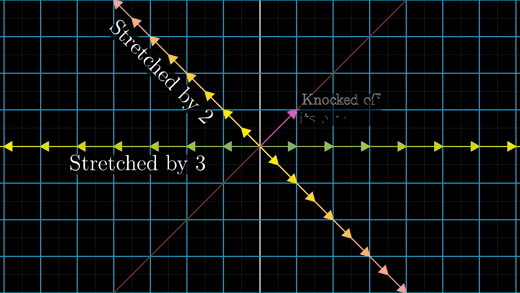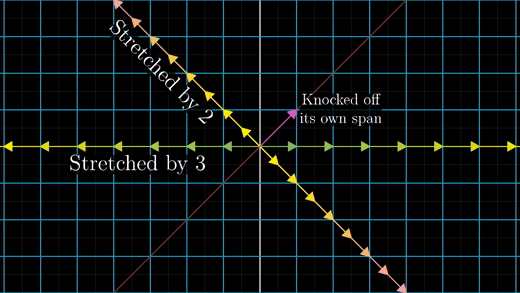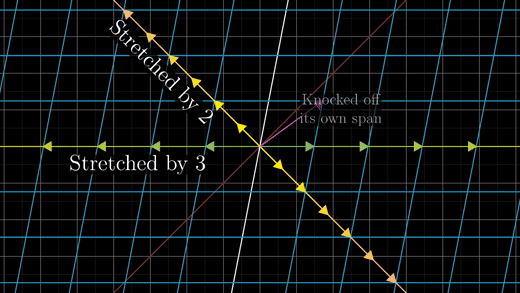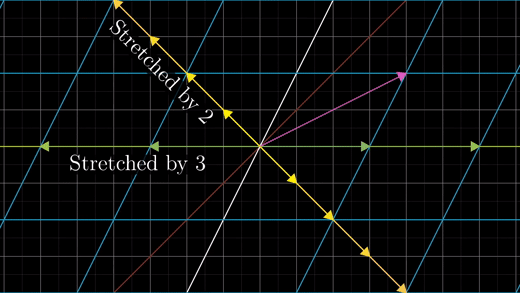
자, 정리해보자. 어떤 행렬 M은 일종의 Transformation으로 해석 가능하다. 이 행렬의 Eigenvector를 찾는 것은, Transformation의 기준이 되는 메인 축을 찾는 것과 같다. Eigenvalue는 메인 축을 기준으로 Scaling되는 정도를 의미한다. 예를 들어, \(\displaystyle M = \left( \begin{matrix} 5 & -2 \\ -2 & 2 \end{matrix} \right)\)라는 행렬이 주어졌을 때, 이것이 무슨 변환을 의미하는 행렬인지 알고 싶다. 이럴 때 Eigenvalue와 Eigenvector를 찾으면 된다. 위 예제의 경우 Eigenvalue는 각각 \(\lambda = 1,6\)이고 Eigenvalue에 대응하는 Eivenvector는 \(\displaystyle \vec{v} = \frac{1}{\sqrt{ 5 }} \left(\begin{matrix} -2 \\ 1 \end{matrix}\right), \frac{1}{\sqrt{ 5 }} \left(\begin{matrix} 1 \\ 2 \end{matrix}\right)\)이다. \((-2, 1)\) 방향의 벡터는 그대로 잡고, \((1, 2)\) 방향의 벡터를 6배만큼 쭉 늘리는 변환을 상상해보라. 그것이 행렬 M이 의미하는 Transformation이다.

만약 Eigenvector가 \(\left(\begin{matrix} 1 \\ -i \\ 0 \end{matrix}\right)\)과 같이 복소수가 포함되어 Eigenvalue of Real Symmtric Matrix있다면, 유클리드 공간 위에서 표현할 방법이 없다. 따라서 직관적으로 상상할 수 없는 복소수까지 포함된 복소 벡터 공간 위에 축이 있다고 생각해야 한다. 공간 자체가 다르므로, 기존의 길이를 구하는 연산을 적용할 수 없다. 복소 벡터 공간 위의 길이를 구하는 연산은 \(\lvert \vec{v} \rvert = \vec{v}^* \cdot \vec{v}\)으로 정의된다.

\(R^{-1} MR\)는 전형적인 Transformation을 적용하는 패턴이다. 같은 Matrix라도 표현되는 Space에 따라 변환의 느낌이 달라질 수 있다. 만약 V Space에서 적용되는 변환 M의 느낌을 W Space에서 똑같이 적용하는 변환 행렬을 얻고 싶다면? 공간을 W Space로 옮긴 후 Transformation을 적용 하고, 다시 V Space로 되돌리면 된다. 이때 사용되는 패턴이 \(R^{-1} MR\)이며, 이 행렬을 모두 행렬 곱 하여 하나의 행렬로 만들면 그 행렬이 V Space에서 M Transform의 느낌 그대로 W Space에서 Transform하는 행렬을 얻어낸다.

만약 어떤 행렬의 Eigenvector를 Column으로 갖는 행렬 R을 정의하고, \(R^{-1}MR\) 행렬을 계산하면, \(\left( \begin{matrix} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{matrix} \right)\)와 같이 대각 성분이 Eigenvalue로 이루어진 대각 행렬을 얻게 된다. 이를 Matrix를 Diagonalization (대각화) 한다고 부른다. 이는 생각해보면 당연한 결과이다. M 행렬의 Eigenvector를 Basis로 갖는 Space에서 M 행렬의 Transformation을 적용하면, 당연히 그 Space에선 그저 Basis Vector를 Eigenvalue만큼 Scaling하는 효과일 뿐이다. 행렬의 대각화의 활용 중 하나는, 행렬의 제곱 연산을 쉽게 할 수 있게 만들어준다. 예를 들어, \(A^{100} = \left( \begin{matrix} 3 & 1 \\ 0 & 2\end{matrix} \right)^{100}\)을 그냥 계산해야 한다면 아주 골치가 아플 것이다. 이때, 고유값을 찾아 대각화한 행렬을 D, 고유벡터를 Column으로 갖는 행렬을 P라고 하면 행렬 A를 \(PDP^{-1}\)로 적을 수 있다. \(A^{100} = (PDP^{-1})(PDP^{-1}) \dots (PDP^{-1}) = PD^{100}P^{-1}\)이고, \(D^{100}\)은 대각 행렬로써 아주 쉽게 계산 할 수 있다.

Eigenvalue, Eigenvector of Real Symmtric Matrix

Eigenvalue가 항상 실수는 아니고, Eigenvector가 항상 직교하는 것은 아니다. 하지만, \(\left( \begin{matrix} 2 & -1 \\ -1 & 2 \end{matrix} \right)\)와 같은 Real Symmtric Matrix는 모든 Eigenvalue가 항상 Real이고, Eigenvector는 모두 Orthogonal함이 보장되는 아주 특별한 행렬이다.. 이를 증명해보자.

[!tip]- All eigenvalues of a real symmetric matrix are always real.{title}

\[\mathbf{M} \vec{v} = \lambda \vec{v}\] \[\Rightarrow \vec{v}^* \cdot \mathbf{M} \vec{v} = \lambda \vec{v}^* \cdot \vec{v}\] \[\Rightarrow (\vec{v}^* \cdot \mathbf{M} \vec{v}) = (\lambda \vec{v}^* \cdot \vec{v})^*\] \[\Rightarrow \vec{v}^* \cdot \mathbf{M}^* \vec{v}^* = \lambda^* \vec{v}^* \cdot \vec{v}^*\] \[\text{M is Real Symmetric Matrix, } \mathbf{M}^* = \mathbf{M}\] \[\Rightarrow \vec{v}^* \cdot \mathbf{M} \vec{v}^* = \lambda^* \vec{v}^* \cdot \vec{v}^*\]

(1) \(\quad \vec{v}^* \cdot \mathbf{M} \vec{v} = \lambda \vec{v}^* \cdot \vec{v}\)

\[= \displaystyle \sum_i V_i^* \displaystyle \sum_j M_{ij} V_j\] \[= \displaystyle \sum_{i,j} V_i^* M_{ij} V_j\]

(2) \(\quad \vec{v} \cdot \mathbf{M} \vec{v}^* = \lambda^* \vec{v} \cdot \vec{v}^*\)

\[= \displaystyle \sum_{i,j} V_i M_{ij} V_j^*\] \[= \displaystyle \sum_{i,j} V_j^* M_{ji} V_i \quad (M_{ij} = M_{ji})\] \[\therefore ~ \lambda \vec{v}^* \cdot \vec{v} = \lambda^* \vec{v} \cdot \vec{v}^* \Rightarrow (\lambda - \lambda^*) \vec{v} \cdot \vec{v}^* = 0\]

이때, \(\vec{v} \cdot \vec{v}^*\)는 복소 벡터 길이의 제곱이며, \(\vec{v}\)는 eigenvector로 영벡터가 아님을 알고 있다. 따라서 길이가 0이 될 수 없으며, 방법은 \(\lambda - \lambda^*=0\)이 되는 수 밖에 없다. 따라서, \(\lambda = \lambda^*\)이며, \(\lambda\)는 Real임을 증명한다.

[!tip]- All eigenvector of a real symmetric matrix are always orthogonal.{title} \(\lambda_{1}, \lambda_{2}\)에 대응하는 Eigenvector를 \(\vec{v}_{1}, \vec{v}_{2}\)라고 하자.

\[\mathbf{M} \vec{v}^{(1)} = \lambda^{(1)} \vec{v}^{(1)}\] \[\Rightarrow \vec{v}^{(1)*} \cdot \mathbf{M} \vec{v}^{(1)} = \lambda^{(1)} \vec{v}^{(1)*} \cdot \vec{v}^{(1)}\] \[= \displaystyle \sum_{i,j} V_i^{(1)*} M_{ij} V_j^{(1)}\] \[\mathbf{M} \vec{v}^{(2)} = \lambda^{(2)} \vec{v}^{(2)}\] \[\Rightarrow \vec{v}^{(2)*} \cdot \mathbf{M} \vec{v}^{(2)} = \lambda^{(2)} \vec{v}^{(2)*} \cdot \vec{v}^{(2)}\] \[\Rightarrow \left( \vec{v}^{(1)*} \cdot \mathbf{M} \vec{v}^{(2)} \right)^* = \left( \lambda^{(1)} \vec{v}^{(1)*} \cdot \vec{v}^{(2)} \right)^*\] \[\Rightarrow \vec{v}^{(1)*} \cdot \mathbf{M} \vec{v}^{(2)*} = \lambda^{(1)*} \vec{v}^{(1)*} \cdot \vec{v}^{(2)*}\] \[\Rightarrow \displaystyle \sum_{i,j} V_i^{(1)} M_{ij} V_j^{(2)*} = \displaystyle \sum_{i,j} V_j^{(2)*} M_{ji} V_i^{(1)}\] \[\therefore ~\lambda^{(1)} \vec{v}^{(2)} \cdot \vec{v}^{(1)} = \lambda^{(2)} \vec{v}^{(1)} \cdot \vec{v}^{(2)*} \Rightarrow (\lambda^{(1)} - \lambda^{(2)}) \vec{v}^{(1)} \cdot \vec{v}^{(2)*} = 0.\]

\(\lambda^{(1)} \neq \lambda^{(2)}\)이므로, \(\vec{v}^{(1)} \cdot \vec{v}^{(2)*} = 0\).