미분적분학 14. 벡터미분적분학
Calculus: Early Transcendentals, 8th의 내용입니다.
Fundamental Theorem of Calculus (적분과 미분의 기본 정리)
함수의 미분을 적분하는 것은, 도메인의 경계값에서 계산하는 것과 같다.
- \(\displaystyle \int_{a}^{b}f'(x)dx = f(b)-f(a)\)
- \(\displaystyle \int_{C}\nabla f(x,y,z) \cdot d\vec{r} = f(\vec{r}_{1})-f(\vec{r}_{0})\)
- \(\displaystyle \iint_{D} (\nabla \times \vec{F}) \cdot d \vec{a} = \oint_{\partial D} \vec{F} \cdot d\vec{r}\) : 스토크스 정리
\(\displaystyle \iiint_{E} \nabla \cdot \vec{F} dV = \iint_{\partial E} \vec{F} \cdot d \vec{a}\) : 발산 정리
- \(\displaystyle \int_{a}^{b}f'(x)dx=\int_{a}^{b} \frac{df(x)}{dx}dx=\int_{a}^{b}df(x)=f(b)-f(a)\)
- \(\displaystyle \nabla f \cdot \vec{r} = \frac{{\partial f}}{\partial x}dx + \frac{{\partial f}}{\partial y}dy + \frac{{\partial z}}{\partial z}dz = df\)이므로, \(\displaystyle \int_{C} \nabla f \cdot d\vec{r} = \int_{C} df(x,y,z) =f(\vec{b})-f(\vec{a})\)
Conservative Vector Field
선적분이 경로에 의존하지 않는 특별한 벡터장이 존재한다. 이떄의 선적분 값은 특별히 \(\displaystyle \Phi(\vec{b})-\Phi(\vec{a}) \equiv - \int^\vec{b}_{\vec{a}} \vec{F}(\vec{r}) \cdot d\vec{r}\) Potential이라고 정의한다. 만약 Vector Field의 다음과 같은 성질이 하나라도 만족되면 자동으로 Vector Field는 Conservative Vector Field임이 보장되며, 다른 모든 성질 또한 만족하게 된다.
- \(\vec{F} = - \nabla \Phi\)인 \(\Phi\)가 존재
- \(\nabla \times \vec{F} = 0\)이고, \(\vec{F}\)의 Domain이 Simply Connected Space일 때.
- 선적분이 경로에 의존하지 않음
이때, Simply Connected Space란 위상수학적으로 줄여서 하나의 점으로 만들 수 있는 공간을 의미한다. 즉 Domain에 구멍이 있어 줄였을 때 한 점으로 만들 수 없다면, \(\vec{F}\)의 Curl이 0이라고 해서 보존장임이 보장되지 않는다. 예를들어, \(\displaystyle \vec{F}=\left( -\frac{y}{x^2+y^2}, \frac{x}{x^2+y^2} \right)\)는 Domain이 \(\mathbb{R}^2-\{(0,0)\}\)으로 원점에 구멍이 있다. 따라서, Curl을 계산해보면 0이지만 벡터장이 보존장이 아닐 수 있다. 실제로 폐곡선을 따라 적분해보면 값이 0이 아닌 다른 값이 나오는 것을 확인할 수 있다. \(C:\vec{r}(t)=(\cos t,\sin t),~0\leq t\leq 2\pi\), \(\displaystyle \oint_C \mathbf{F} \cdot d\mathbf{r} = \int_0^{2\pi} \left( \frac{-\sin t}{\cos^2 t + \sin^2 t}, \frac{\cos t}{\cos^2 t + \sin^2 t} \right) \cdot (-\sin t, \cos t) \, dt = \int_0^{2\pi} dt = 2\pi\)
도메인이 Simply Connected Space가 아니고 Curl이 0이어도 벡터장이 보존장일 수 있다. 비록 Curl이 0이라는 정보를 통해 알아내는 것은 아니고, \(\vec{F}=\nabla f\)를 만족하는 퍼텐셜 함수를 찾아내면 보존장이다.
\[\displaystyle \vec{F}(x,y,z) = \left( \frac{x}{ \sqrt{ x^2+y^2+z^2 } }, \frac{y}{\sqrt{ x^2+y^2+z^2 }}, \frac{z}{\sqrt{ x^2+y^2+z^2 }} \right)\]예를들어 위 함수는 도메인이 원점에서 구멍이 뚫려있어 Simply Connected Space가 아니지만, 퍼텐셜 함수가 \(f=\sqrt{ x^2+y^2+z^2 }\)로 존재하기 때문에, \(\vec{F}\)가 보존장이다.
Find Potential Function
\(\vec{F} = \nabla f\)를 만족할 때, 포텐셜 함수 \(f\)를 찾는 방법은, 그냥 \(\partial_{x}f=F_{x}\), \(\partial_{y}f = F_{y}\), \(\partial_zf =F_{z}\)임을 이용하여 부정적분을 세번 해보면 된다. 각각 부정적분해보면 \(\displaystyle f = \int F_{x}dx + g(y,z)\), \(\displaystyle f = \int F_{y}dy + h(x,z)\), \(\displaystyle f = \int F_{z}dz + k(x,y)\)라는 3개의 식을 얻게 되고, 이 3개의 식을 비교해서 포텐셜 함수 \(f\)를 구할 수 있다.
Line Integral
벡터 함수의 선적분은 \(\displaystyle \int_{C} \vec{F}(x,y,z) \cdot d\vec{r}\)이다. 똑같이, Domain \(C\) 공간에서 적분하는 것을 \([a, b]\) Domain으로 바꿔줘야 하며, \((x,y,z)=\vec{r}(t)\) 변환 함수를 사용한다. 이때 기저의 Scaling Factor는 다음과 같다.
\[\frac{\partial (x,y,z)}{\partial t}= \left[ \begin{matrix} \frac{{\partial x}}{\partial t} \\ \frac{{\partial y}}{\partial t} \\ \frac{{\partial z}}{\partial t}\end{matrix} \right] = \vec{r}'(t)\]\(d\vec{r}\)가 방향성이 중요하므로 Norm을 취하지 않으므로 최종 식은 다음과 같다.
\[\int_{C} \vec{F}(x,y,z) \cdot d\vec{r} = \int^{t_{1}}_{t_{0}} \vec{F}(x,y,z) \cdot \vec{r}'(t) dt\]이것 말고 다른 방법으로 계산하는 방법이 세가지가 존재한다.
- \(\displaystyle d\vec{r} = \frac{d\vec{r}(t)}{dt} dt = \vec{r}'(t)dt\)
- \(d\vec{r} = \vec{T}(t)ds\)임을 이용한다. 그림을 그려보면 바로 이해할 수 있다. \(\displaystyle \int_{C} \vec{F}(x,y,z) \cdot d\vec{r} = \int_{C} \vec{F}(x,y,z) \cdot \vec{T}(t)ds = \int^{t_{1}}_{t_{0}}\vec{F}(\vec{r}(t)) \cdot \frac{\vec{r}'(t)}{\lvert \vec{r}'(t) \rvert} \lvert \vec{r}'(t) \rvert dt = \int^{t_{1}}_{t_{0}} \vec{F}(\vec{r}(t)) \cdot \vec{r}'(t) dt\)
- \(d\vec{r} = (dx,dy,dz)\)임을 이용하여, 직접 내적을 때려버린다. \(\vec{F}(x,y,z)=(f(x,y,z),g(x,y,z),h(x,y,z))\)로 기술된다면, \(\displaystyle \int_{C} \vec{F}(x,y,z) \cdot d\vec{r} = \int_{C}f dx + gdy + hdz = \int^{t_{1}}_{t_{0}}fx'(t)dt + gy'(t)dt + hz'(t)dt\)’
기저에 방향이 없다면, \(\displaystyle \int_{-C} = \int_{C}\)는 같다. 기저에 방향이 의미가 있다면, 마이너스가 붙는다. \(\displaystyle \int_{-C} = -\int_{C}\) 예를들어, \(ds\)는 방향성이 없으므로 \(\displaystyle \int_{-C} f ds = \int_{C}f ds\) 이고, \(dx, dy, d\vec{r}\) 등은 방향성이 있으므로 \(\displaystyle \int_{-C}f dx = -\int_{C}f dx\), \(\displaystyle \int_{-C} \vec{F} \cdot d \vec{r} = -\int_{C} \vec{F} \cdot d\vec{r}\)이다.
Green’s theorem, Stokes’ theorem
- Green’s theorem : \(\displaystyle \iint_{S} \left( \frac{{\partial F_{y}}}{\partial x} - \frac{{\partial F_{x}}}{\partial y} \right) dA= \oint_{C}\vec{F}(x,y) \cdot d\vec{r}\)
- Stokes’ theorem : \(\displaystyle \iint_{S} (\nabla \times \vec{F}(x,y,z)) \cdot d \vec{a}= \oint_{C}\vec{F}(x,y,z) \cdot d\vec{r}\)
그냥 Stokes’ theorem의 2차원 버전이 Green’s theorem이고, Stokes’ theorem이 더 일반적인 정리다. 이때 Area S는 Simply Connected이어야 하고, 곡선 C는 Simple curve어야 한다. Simple curve는, 곡선을 한붓그리기로 그렸을 때 만나는 지점이 시작과 끝점만 있는 곡선이다. 곡선이 중간에서 만나는 지점이 있다면 Simple curve가 아니다.
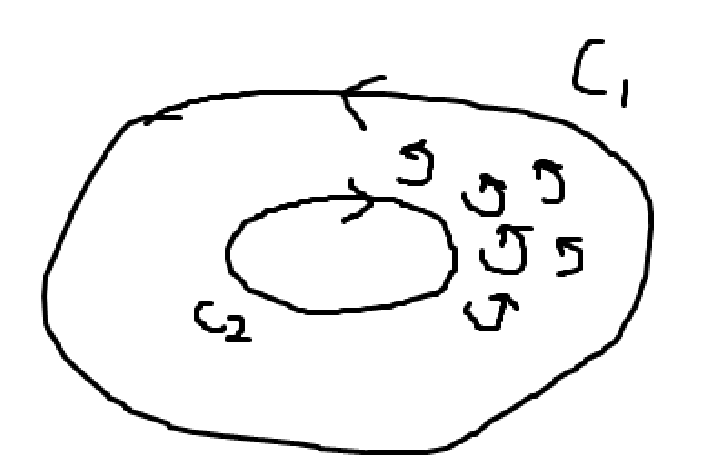
만약 S가 Simply Connected가 아닌 경우, 즉 영역 안에 구멍이 있는 경우는 바깥의 곡선의 방향을 반시계, 안쪽의 곡선의 방향을 시계 방향으로 잡으면 \(\partial D = C_{1} \cup C_{2}\)로 잡고 계산하면 된다. 곡선의 방향이 반대인 이유는, 스토크스 정리의 의미를 생각해보면 당연한 결과다. 스토크스 정리는 벡터장의 미소 영역 회전량을 모두 더하면 닫힌 경로의 경계값을 크게 한번 적분한 것과 같다는 것. 그 이유는 안쪽의 회전양은 다른 인접한 회전양에 의해 상쇄되기 떄문에 경계값만 남기 때문이다. 그 방향을 따져보면, 안쪽의 경로 방향은 바깥쪽과 당연히 반대방향이 되어야 부호가 일관성이 있다.
이 정리의 Use Case로는, 양방향으로 사용 가능. 어떤 닫힌 경로의 복잡한 선적분을 2중 적분으로 바꿔서 적분하는데 사용할 수도 있고, 미분한 함수의 면적분을 단순히 경계의 선적분으로 바꾸고 싶을 때 사용할 수도 있다. 왜 굳이 1차원 선적분을 2차원 면적분으로 바꿔서 계산하는 경우가 있냐? 싶겠지만 2차원 적분으로 바꾸면 공간을 변환해도 면적분한 값은 자코비안만 곱하면 같은 적분값이 됨을 이용하여 더 쉽게 적분할 수 있다. 또는, 닫힌 경로를 여러번의 적분을 통해 구할 수 있는 경우 한번의 면적분만으로도 구할 수도 있다. (폐곡선을 적분하려면 곡선을 쪼개서 선적분을 두번해야하는데 그것을 한번의 면적분만으로 구할 수 있게 된다.)
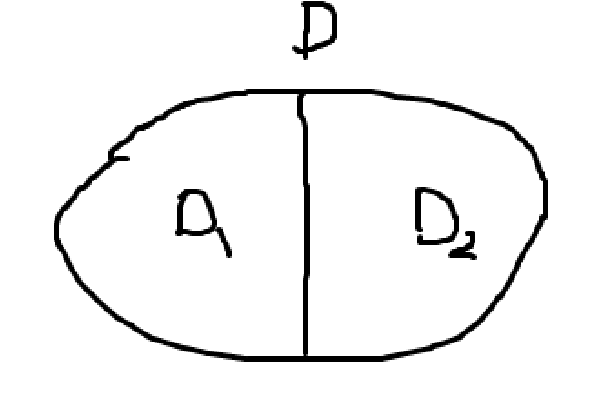
영역 D를 \(D_{1}, D_{2}\) 두 부분으로 쪼개서 각각 면적분 한 뒤에 더해도 그 결과는 전체 경계 곡선 \(\partial D\)를 선적분한 것과 같다. 그 이유는 \(D_1\), \(D_2\)가 공유하는 곡선의 선적분 결과는 상쇄되기 때문이다.
Surface Integral on Scalar Field
곡면은 2변수 벡터함수 또는 2변수 스칼라함수로 표현될 수 있다. 임의의 곡면 S를 중적분하기 위해서는, 곡면 S를 매개화하는 매개변수 \((x,y,z) = \vec{r}(u,v)\)를 찾아서 공간을 변환하면 적분 가능해진다.
\[\displaystyle \iint_{S} f(x,y,z)dA = \iint_{S} f(\vec{r}(u,v)) \left\lvert {\frac{\partial(x,y,z)}{\partial(u,v)}} \right\rvert dudv\]그런데 자코비안을 계산해보면, 자코비안 행렬식이 3x2가 나와 행렬식을 계산할 수 없다. \(\displaystyle {\frac{\partial(x,y,z)}{\partial(u,v)}} = \left\lvert \begin{matrix} \frac{{\partial x}}{\partial u} & \frac{{\partial x}}{\partial v} \\ \frac{{\partial y}}{\partial u} & \frac{{\partial y}}{\partial v} \\ \frac{{\partial z}}{\partial u} & \frac{{\partial z}}{\partial v}\end{matrix} \right\rvert\) 이것을 원래는 계산할 수 없지만, 다음과 같은 방법을 사용하면 값을 구할 수 있다.
- 열벡터를 취한다.
- 두 열벡터를 외적한 결과의 크기를 구한다.
열벡터의 의미는 \(\vec{r}(u,v)\)를 한 변수에 대해 편미분한 것과 같다. \(\displaystyle \frac{{\partial \vec{r}}}{\partial u}\), \(\displaystyle \frac{{\partial \vec{r}}}{\partial v}\)는 곡면 위의 한 점 \((u,v)\) 위의 u 방향의 접선벡터, v 방향의 접선벡터를 의미한다. 접선벡터의 외적의 크기는, 두 접선 벡터가 만드는 평행사변형의 넓이와 같다. 이는 공간의 Scaling Factor와 같다. 따라서 일반적으로 \(\displaystyle \frac{{\partial(x,y,z)}}{\partial(u,v)} = \vec{r}_{u} \times \vec{r}_{v}\)와 같다.
[!tip]- Domain Surface가 \(z=x^2+y\)와 같이 \(z=g(x,y)\)로 주어질 때{title} \(\vec{r}(x,y)=(x,y,z)=(x,y,g(x,y))\)로 변환함수를 만들 수 있다.
\[\displaystyle \frac{\partial (x,y,z)}{\partial (x, y)} = \begin{bmatrix} \frac{\partial x}{\partial x} & \frac{\partial x}{\partial y} \\ \frac{\partial y}{\partial x} & \frac{\partial y}{\partial y} \\ \frac{\partial z}{\partial x} & \frac{\partial z}{\partial y} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \frac{\partial g(x, y)}{\partial x} & \frac{\partial g(x, y)}{\partial y} \end{bmatrix}\]자코비안은 위와 같고, 행렬식은 \(\lvert (1,0,g_{x}) \times (0,1,g_{y}) \rvert\)와 같다. 계산하면 \(\sqrt{ 1+g_{x}^2+g_{y}^2 }\)이다. 결론적으로, \(z=g(x,y)\)꼴로 Domain Surface가 주어지면 자코비안 Factor를 \(\sqrt{ 1+g_{x}^2+g_{y}^2 }\)를 사용하면 된다.
\[\therefore ~ \iint_{S}f(x,y,z)dA = \iint_S f(x, y, g(x, y)) (\sqrt{1 + g_x^2 + g_y^2}) dA\]
Oriented Surface
방향을 정할 수 있는 곡면을 Orientable Surface라고 하고, 방향이 부여된 곡면을 Oriented Surface (유향 곡면)이라고 한다.
Surface Integral on Vector Field
똑같이 Domain을 매개화하는 매개함수 \(\vec{r}(u,v)\)를 정의하여 공간 변환 후 적분하면 된다.
\[\iint_{S} \vec{A} \cdot d \vec{a} = \iint_{S} \vec{A}(\vec{r}(u,v)) \cdot \frac{\partial(x,y,z)}{\partial(u,v)}da = \iint_{S} \vec{A}(\vec{r}(u,v)) \cdot (\vec{r}_{u} \times \vec{r}_{v}) da\]Vector Field를 중적분할 때 \(\displaystyle \iint_{S} \vec{A} \cdot d\vec{a} = \iint_{S} \vec{A} \cdot \hat{n} da\)일 때 \(\vec{n}\)의 정체는 미소 평면의 단위 법벡터이며, \(\displaystyle \hat{n}(x,y,z) = \frac{\vec{r}_{x} \times \vec{r}_{y}}{\lvert \vec{r}_{x} \times \vec{r}_{y} \rvert}\)로 정의한다. \(\hat{n}\)은 상수 벡터가 아니다. \(\vec{r}\) 위치에서의 미소 평면의 단위 법벡터를 의미한다.
만약 곡면 S가 평면이고, 직관적으로 곡면에 대한 법선벡터 \(\vec{n}\)를 찾았다면 \(\vec{n}\)는 상수 벡터가 될 것이고 \(\displaystyle\hat{n}(x,y,z) = \frac{\vec{n}}{\lvert \vec{n} \rvert}\)와 같다. 따라서 \(\vec{r}(u,v)\) 함수로 합성해도 \(\displaystyle \hat{n}(\vec{r}(u,v)) = \frac{\hat{n}}{\lvert \vec{n} \rvert}\)로 바뀌지 않는다. 이런 경우는 굳이 \(\vec{r}_{u} \times \vec{r}_{v}\)를 계산하지 않아도 \(\displaystyle \iint_{S} \vec{A}(\vec{r}(u,v)) \cdot \hat{n} da\)를 사용하여 바로 계산할 수 있다. 그 근거는 다음과 같다.
\[\iint_{S} \vec{A} \cdot \hat{n} da = \iint_{S} \vec{A}(\vec{r}(u,v)) \cdot \hat{n} (\vec{r}(u,v))\lvert \vec{r}_{u} \times \vec{r}_{v} \rvert da\] \[= \iint_{S} \vec{A}(\vec{r}) \cdot \frac{\vec{r}_{u} \times \vec{r}_{v}}{\lvert \vec{r}_{u} \times \vec{r}_{v} \rvert}\lvert \vec{r}_{u} \times \vec{r}_{v} \rvert da = \iint_{S} \vec{A}(\vec{r}) \cdot \vec{r}_{u} \times \vec{r}_{v} da\][!tip]- 곡면의 경계가 같다면, \(\nabla \times \vec{A}\)를 면적분한 결과는 똑같다.{title} Stokes’ Theorem으로 알 수 있는 것은 경계가 같다면, 곡면이 어떻게 생기던간에 \(\nabla \times \vec{A}\)를 적분한 결과가 같다는 것이다. 따라서 닫힌 곡선 선적분 -> 곡면 중적분으로 바꿀 때 최대한 간단한 곡면 S를 잡는게 유리하다.
곡면의 접평면
곡면 S위의 점 P에서 접하는 접평면 \(T_{P}S\)는 다음과 같이 구할 수 있다.
- 점 \(P(u,v)\) 위의 두 접벡터를 두 변수에 대해 편미분하여 구한다. \(\displaystyle \frac{{\partial \vec{r}(u,v)}}{\partial u}\), \(\displaystyle \frac{{\partial \vec{r}}(u,v)}{\partial v}\)
- 두 접벡터를 외적하여 두 접벡터에 수직한 벡터 \(\vec{n}\)를 구한다.
- 평면의 법선벡터 \(\vec{n}=(a,b,c)\)와 평면 위의 한 점 \(P(x,y,z)\)를 알면 평면의 방정식을 얻을 수 있다. \(T_{P}S : a(x-x_{0})+b(y-y_{0})+z(z-z_{0})=0\)
발산 정리
만약 체적 안에 작은 체적이 있고, 체적의 Boundry Surface의 방향은 바깥쪽 방향이고 내부의 작운 체적의 Boundry Surface의 방향이 안쪽 방향으로 잡으면 전체 - 작은 체적 = E라고 헀을때 여전히 발산 정리가 성립한다.
\[\int_{E} \nabla \cdot \vec{F} d\tau = \oint_{\partial E} \vec{F} \cdot d\vec{a}\]