미분적분학 13. 다중적분
Calculus: Early Transcendentals, 8th의 내용입니다.
스칼라 함수의 면적분, 부피적분
만약 적분할 영역이 직사각형 같이 간단하다면, 바로 Fubini 정리를 사용하여 적분하면 된다. 이때 적분 대상이 될 함수가 분리 가능하다면, 따로따로 적분을 적용할 수 있다.
\[\iint_{R} f(x,y) dA = \int_{a}^{b} \int_{c}^{d} f(x,y) dydx = \int_{c}^{d}\int_{a}^{b} f(x,y) dxdy\]적분할 영역이 어렵다면, 다른 공간으로 변환 후 적분하는 것이 더 편할 수 있다는 아이디어를 사용한다. 공간을 변환하면, 적분 범위와 \(dA, dV\)가 \(\lvert Jac(\vec{T}) \rvert dA, \lvert Jac(\vec{T}) \rvert dV\)로 바뀐다. \(\iiint_{E} f dV = \iiint_{B} (f \circ \vec{T}) \cdot \lvert Jac(\vec{T}) \rvert dV\) 일반적으로 변환은 n차원 공간에서 n차원 공간의 변환을 적용해야 하므로, 변환을 의미하는 함수는 벡터 함수가 되어야 한다.
2중 적분, 면적분의 경우 적분할 영역이 부채꼴 모양이면 극좌표 변환을 적용하면 더 편하게 적분할 수 있다. 그때 사용되는 변환 함수는 \((x,y) = \vec{T}(r, \theta) = (r\cos \theta, r\sin \theta)\)와 같다.
3중 적분, 체적적분의 경우 영역이 원통, 구와 같은 모양이면 원통 좌표계 변환, 구면 좌표계 변환을 적용할 수 있다. 각각 변환 함수는 \((x,y,z) = \vec{T}_{c}(r,\theta,z)=(r\cos \theta,r\sin \theta,z)\), \((x,y,z) = \vec{T}_{s}(r,\theta,\phi) = (r\sin \theta \cos \phi, r\sin \theta \sin \phi, r\cos \theta)\)를 사용한다.
구면 좌표계의 \(\theta\) 범위는 \(0 \sim \pi\)로 잡고, \(\theta\)의 범위를 \(0~2\pi\)로 잡는 이유가 무엇인가? 한쪽이 \(2\pi\)로 돌면, 한쪽은 \(\pi\)만큼만 돌아도 구 전체를 표현할 수 있기 때문이다.
만약 적분의 범위가 \(0 \leq x \leq 4\), \(x \leq y \leq x^2\), \(x+y \leq z \leq x^2 + y^2\)와 같이 다른 변수에 의존되어 주어지면, \(\displaystyle \int_{0}^{4} \int_{x}^{x^2} \int_{x+y}^{x^2+y^2} f(x,y,z) dzdydx\) 이렇게 최종 적분의 결과가 상수가 되도록 적분 순서를 잘 정하면 된다.
Jacobian
자코비안 행렬은, 벡터를 입력받는 벡터 함수를 미분하여 얻어내는 행렬이다. 만약 함수 \(\vec{T}\)가 (x,y,z) 기저를 (u,v,w)로 바꾸는 변환 함수라고 하면, \(\vec{T}(u,v,w) = (x,y,z)\)와 같은 벡터 함수이다. 이런 변환의 자코비안은 다음과 같다.
\[Jac = \det\left( \frac{{\partial(\text{변환 전 변수들})}}{\partial(\text{변환 후 변수들})} \right)= \det \left( \frac{{\partial(x,y,z)}}{\partial(u,v,w)}\right) = \left \lvert \begin{matrix} \frac{{\partial x}}{\partial u} & \frac{{\partial x}}{\partial v} & \frac{{\partial x}}{\partial w} \\ \frac{{\partial y}}{\partial u} & \frac{{\partial y}}{\partial v} & \frac{{\partial y}}{\partial w} \\ \frac{{\partial z}}{\partial u} & \frac{{\partial z}}{\partial v} &\frac{{\partial z}}{\partial w} \end{matrix} \right \rvert\]선형변환의 행렬식의 절댓값이 변환 후 공간의 Scaling된 Factor 값으로 해석할 수 있듯이, 자코비안 행렬식의 절댓값은 일반적인 변환 후의 공간이 Scaling된 Factor 값으로 해석할 수 있다. 이때 절댓값을 붙이는 이유는 크기의 감소 증가만 보기 위함이며, 음수의 의미는 공간이 뒤집혔냐 안뒤집혔냐의 의미로 해석할 수 있다.
예를들어, 기존 공간에서의 기저가 \(dV=dxdydz\)로 표현될 떄 변환된 후 공간이 Scaling되는 Factor값을 곱해야 하는데, 그 값은 \(dxdydz = \displaystyle \left\lvert \frac{{\partial(x,y,z)}}{\partial(u,v,w)} \right\rvert dudvdw\)와 같다.
[!information]- 이를 증명하는 과정은 다음과 같다.{title}
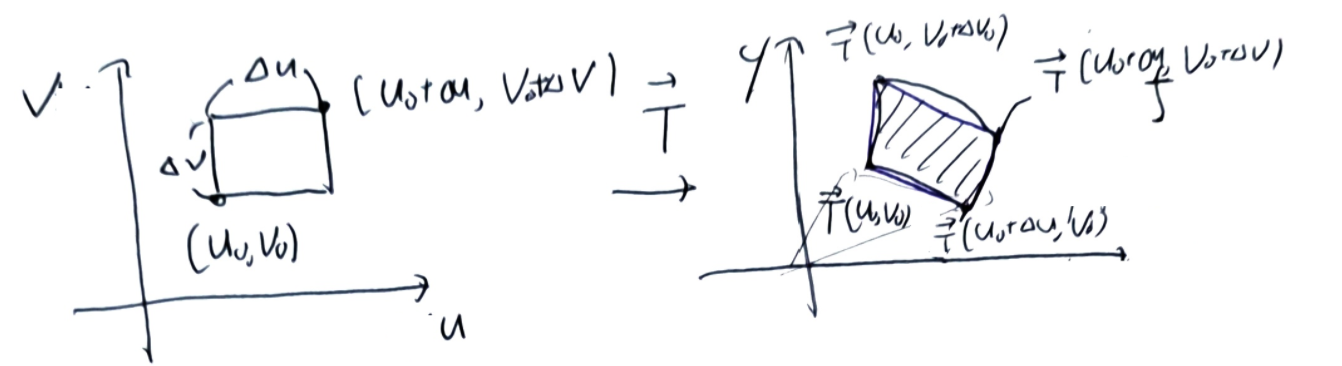
\(\Delta A = \Delta u \Delta v\)의 \(\vec{T}\) 변환 후 \(\Delta A\)의 변형된 넓이는 평행사변형으로 근사 가능.
\[\text{평행사변형의 넓이}= \left\lvert \left( \vec{T}(u_0 + \Delta u, v_0) - \vec{T}(u_0, v_0) \right) \times \left( \vec{T}(u_0, v_0 + \Delta v) - \vec{T}(u_0, v_0) \right) \right\rvert\] \[= \left\lvert \left( \frac{\partial \vec{T}}{\partial u} \Delta u \right) \times \left( \frac{\partial \vec{T}}{\partial v} \Delta v \right) \right\rvert= \left\lvert \Delta u \Delta v \right\rvert \left\lvert \frac{\partial \vec{T}}{\partial u} \times \frac{\partial \vec{T}}{\partial v} \right\rvert\] \[= \left\lvert \Delta u \Delta v \right\rvert \left\lvert \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{vmatrix} \right\rvert= \left\lvert \text{Jac} \right\rvert \left\lvert \Delta A \right\rvert\]
[!example] \(x=r\cos \theta\), \(y=r\sin \theta\)일 때 Jacobian{title} \((x, y) \to (r\cos \theta, r\sin \theta)\)이고, 기저를 \((x,y)\)에서 \((r, \theta)\)로 변환될 때 자코비안은 다음과 같다.
\[\det\left( \frac{\partial(x,y)}{\partial(r,\theta)} \right) = \det\begin{pmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{pmatrix} = \det\begin{pmatrix} \cos \theta & -r\sin \theta \\ \sin \theta & r\cos \theta \end{pmatrix} = r\]
- Jacobian에 대한 추가 깨달음 : 미분적분학 13. 다중적분의 Line Integral 참고
곡면의 넓이
곡면은 세가지 방법으로 표현할 수 있다.
- 2개의 스칼라를 입력으로 받는 스칼라 함수를 x, y, f(x,y) 그래프를 그려보면 이것을 곡면으로 해석할 수 있다.
- 2개의 스칼라를 입력으로 받아 3차원 벡터를 반환하는 벡터 함수를 원점을 고정하고 모든 벡터를 그려보면, 곡면으로 해석할 수 있다.
- 3개의 스칼라를 입력으로 받는 스칼라 함수의 음함수 꼴 \(f(x,y,z)=c\)는 등위 곡면과 같다. 이때, 첫번째 Case의 곡면의 넓이는 다음과 같다.
\(S=\{ (x,y,z) \in \mathbb{R}^3 \mid (x,y) \in D, z = f(x,y) \}\)로 곡면이 주어질때, 그 넓이 \(A(S)\)는 다음과 같다.
\[A(S) = \iint_{D} \sqrt{ 1+ (f_{x})^2 + (f_{y})^2 }dA\][!tip]- 유도 과정{title}
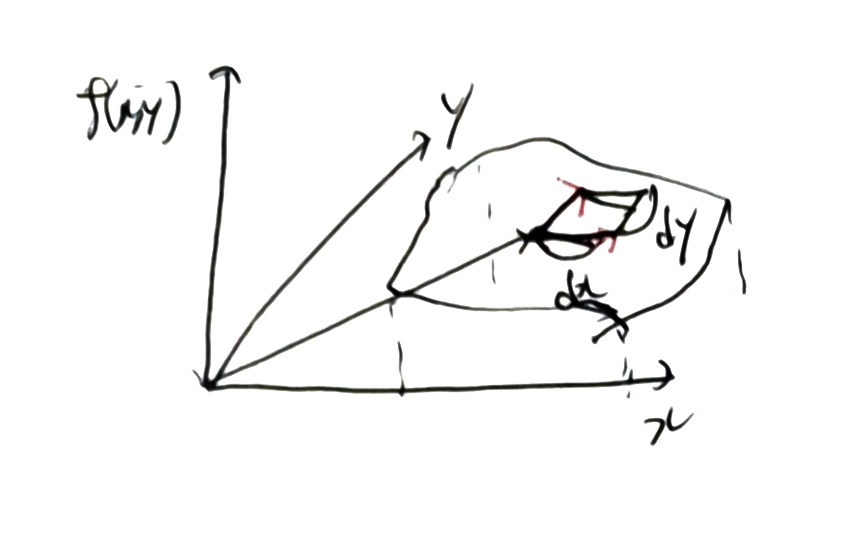
아이디어는 간단하다. 곡면 위의 미소 평면을 모두 더하면 된다.
이 작은 평행 사변형의 넓이는, 두 벡터의 외적의 절대값과 같다.
\[\displaystyle \left\lvert (\begin{pmatrix} x + dx, y, f(x + dx, y) \end{pmatrix} - \begin{pmatrix} x, y, f(x, y) \end{pmatrix}) \times (\begin{pmatrix} x, y + dy, f(x, y + dy) \end{pmatrix} - \begin{pmatrix} x, y, f(x, y) \end{pmatrix}) \right\rvert\] \[= \displaystyle \left\lvert \begin{pmatrix} dx, 0, f(x + dx, y) - f(x, y) \end{pmatrix} \times \begin{pmatrix} 0, dy, f(x, y + dy) - f(x, y) \end{pmatrix} \right\rvert\] \[= \displaystyle \left\lvert \begin{pmatrix} dx, 0, \frac{\partial f}{\partial x} dx \end{pmatrix} \times \begin{pmatrix} 0, dy, \frac{\partial f}{\partial y} dy \end{pmatrix} \right\rvert= \displaystyle \left\lvert \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ dx & 0 & \frac{\partial f}{\partial x} dx \\ 0 & dy & \frac{\partial f}{\partial y} dy \end{vmatrix} \right\rvert\] \[= \displaystyle \left\lvert \begin{pmatrix} 0 - \frac{\partial f}{\partial x} dx dy, - \frac{\partial f}{\partial y} dx dy, dx dy \end{pmatrix} \right\rvert\] \[= \displaystyle \left\lvert \begin{pmatrix} - \frac{\partial f}{\partial x} dx dy, \frac{\partial f}{\partial y} dx dy, dx dy \end{pmatrix} \right\rvert\] \[= \displaystyle \sqrt{ \left( \frac{\partial f}{\partial x} dx dy \right)^2 + \left( \frac{\partial f}{\partial y} dx dy \right)^2 + (dx dy)^2 }\] \[= \displaystyle \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \, dA\]
[!example]- \(S=\{ (x,y,z) \in \mathbb{R}^3 \mid z = x^2 + y^2, z\leq 9 \}\)의 넓이{title} D는 반지름을 3으로 갖는 x, y 평면 위의 원과 같다. \(f_{x} = 2x\), \(f_{y} = 2y\)
\[\displaystyle A(S) = \iint_{D} \sqrt{ 1 + (2x)^2 + (2y)^2 } dA\] \[\displaystyle = \int_{0}^{2\pi} \int_{0}^{3} \sqrt{ 1 + (2r \cos \theta)^2 + (2r \sin \theta)^2 } r dr d\theta\] \[\displaystyle = \int_{0}^{2\pi} \int_{0}^{3} \sqrt{ 1+4r^2 } r dr d\theta\] \[\displaystyle = \int_{0}^{2\pi} d\theta \cdot \int_{0}^{3} r \sqrt{ 1+4r^2 } dr\] \[\displaystyle = \frac{\pi}{6} (37 \sqrt{ 37 } -1)\]
함수의 근사
\(y=f(x)\)와 같은 함수는 어떤 \(x_{0}\) 값 근처에서는 \(f(x) \simeq f'(x_{_{0}})(x-x_{0})+f(x_{0})\)과 같은 접선의 방정식을 사용해도 충분히 괜찮은 근사값을 얻을 수 있다. \(y=f(x)\)는 컴퓨터로 계산하기 오래 걸리는 함수라고 하면, 접선의 방정식을 미리 구해두면 계산 양을 줄일 수 있을 것이다.
위의 논리를 2변수, 3변수 이상의 함수에서도 같은 논리를 적용할 수 있다. \(\vec{r} = (u, v, w)\)라고 하고 \(\vec{r}_{0} = (u_{0}, v_{0}, w_{0})\)라고 하자. 만약 함수가 스칼라 함수라면, \(f(u,v,w) \simeq \nabla f(\vec{r}_{0}) \cdot (\vec{r} - \vec{r}_{0}) + f(\vec{r}_{0})\)은 \(\vec{r}_{0}\) 근처에서 \(f(u, v, w)\) 함수의 괜찮은 근삿값을 구해준다. 만약 함수가 벡터 함수라면, \(\vec{T}(u,v,w) \simeq Jac(\vec{T})(\vec{r}_{0}) \cdot (\vec{r} - \vec{r}_{0}) + \vec{T}(\vec{r}_{0})\)을 사용하면 괜찮은 근삿값을 얻을 수 있다. 여기서 깨닫는 점은, 함수의 미분에 대응되는 것이 스칼라 함수에서 그라디언트라면, 벡터 함수에선 자코비안이라는 점이다.
Line Integral
스칼라 함수의 선적분 \(\displaystyle \int_{C}f(x,y,z)ds\)은 어떻게 계산할 수 있을까? 결론은 다음과 같다.
\[\displaystyle \int_{C}f(x,y,z)ds = \int^{t_{1}}_{t_{0}}f(\vec{r}(t)) \lvert \vec{r}'(t) \rvert dt\]계산을 위해, Domain \(C\) 공간에서 적분하는 것을 \([a, b]\) Domain으로 바꿔야 적분이 가능하다. 즉, 공간의 변환이 필요하며, 변환 함수 \((x,y,z)=\vec{r}(t)\) 로 공간을 변환한다. 기저가 \(s \to t\)로 바뀌면서, 곱해지는 Scale Factor는 \(\lvert \vec{r}'(t) \rvert\)이다. 왜 Scaling Factor가 \(\lvert \vec{r}'(t) \rvert\)인지 생각하는 방법이 세가지가 있다.
- 자코비안 \(\displaystyle \left\lvert \frac{\partial{(x,y,z)}}{\partial t} \right\rvert= \left\lvert \left[ \begin{matrix} \frac{{\partial x}}{\partial t} \\ \frac{{\partial y}}{\partial t} \\ \frac{{\partial z}}{\partial t}\end{matrix} \right] \right\rvert = \lvert \vec{r}'(t) \rvert\)
- 호의 길이 함수 \(\displaystyle s(t)=\int_{t_{0}}^t \lvert \vec{r}'(t') \rvert dt' \implies \frac{ds}{dt} dt=\lvert \vec{r}'(t) \rvert dt\)
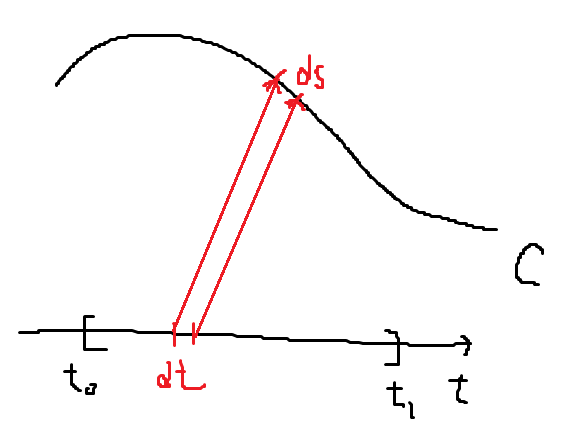
기하학적 직관 \(ds = \lvert \vec{r}'(t) \rvert dt\)
추가로, 각 변수에 대한 선적분을 따로 하는 경우 \(\displaystyle \int_{C} f(x,y,z)dx = \int^{t_{1}}_{t_{2}}f(\vec{r}(t)) x'(t)dt\)이고, y, z일 때도 동일하다. 그 이유는, 기저가 \(x\to t\)로 변화할 때 자코비안은 \(\displaystyle \frac{{\partial x}}{\partial t}\)이다. \(dx\)는 방향성에 따라 적분 결과가 달라지므로, \(\lvert \rvert\)을 붙이지 않고 \(\displaystyle \int_{C} f(x,y,z)dx = \int^{t_{1}}_{t_{2}}f(\vec{r}(t)) x'(t)dt\)로 쓰는 것이다. 여기서 알 수 있는 점이 두가지가 있다. 첫번째는, Scaling Factor의 Jacobian을 구할 때 자코비안을 분자에 변환 전 기저, 분모에 변환 후 기저를 쓰는 것이 편하다는 것. 두번째는, 기저가 \(dx\)와 같이 방향성이 중요하면 Jacobian에 Norm을 붙이지 않고, \(ds, dA, dV\)와 같이 방향성이 없다면 Jacobian에 Norm을 붙인다는 것.