기초전자기학 9. 발전기의 원리는 무엇인가
발전기의 원리는 무엇인가?
자기장 속에서 도선을 움직이면, 도선 속에 들어있는 전하는 자기장에 대해 상대적으로 움직이게 된다. 따라서, 로렌츠 힘 \(\vec{f} = \vec{v} \times \vec{B}\)를 받는다. 그 로렌츠 힘이 기전력 \(\varepsilon = \oint \vec{f} \cdot d\vec{l}\)를 만들어 도선에 전류가 흐르게 된다.
예를들어, 자기장에 일부만 걸치고 오른쪽으로 속도 \(v\)로 움직이는 도선이 있다. 이때 만들어지는 기전력은 다음과 같다.
\[\varepsilon = \oint \vec{f} \cdot d\vec{l} = \oint (\vec{v} \times \vec{B}) \cdot d\vec{l} = vB\int_{a}^{b} \hat{y} \cdot d\vec{l} = vBh\]\(b,c\)와 \(a,d\) 도선 부분은 도선 방향과 수직으로 힘을 받기 때문에 기전력을 만들어내지 않는다. 전하가 도선과 수직 방향으로 움직여봤자 의미가 없기 때문이다.
만약 위 그림에서, 아주 큰 자기장 영역 위의 도선을 움직이게 하면 기전력이 생길까?
운동 기전력에 대한 선속 규칙(flux rule) 으로 쉽게 설명할 수 있다. 닫힌 도선이 만드는 면적 \(S\)를 지나는 자기 선속을 다음과 같이 정의하자.
\[\Phi \equiv \int_{S} \vec{B} \cdot d\vec{a}\]만들어지는 기전력은, 선속의 시간변화의 마이너스와 같다.
\[\varepsilon = - \frac{d\Phi}{dt}\]도선을 포함한 균일한 자기장 영역에서 도선을 움직인다면, 자기 선속 변화율이 없을 것이므로 기전력이 만들어지지 않는다.
왜 기전력은 자기 선속 시간 변화의 음수와 같은가?
도선이 시간에 따라 변화할 수 있는 일반적인 도선에 대해 증명해보자. 임의의 도선을 통과하는 자기 선속을 시간에 대한 함수 \(\Phi(t)\)로 쓸 수 있다. 도선을 통과하는 자기 선속의 변화는 다음과 같다.
\[d\Phi = \Phi(t+dt) - \Phi(t) = \Phi_{\text{띠}} = \int_{\text{띠}} \vec{B} \cdot d\vec{a}\]도선의 이동 방향을 \(\vec{v}\)라고 할 때, 띠의 미소 면적은 \(d\vec{a} = \vec{v} dt \times d\vec{l} = (\vec{v} \times d\vec{l})dt\)와 같다. 평행사변형의 면적은 두 벡터를 외적한 것과 같다. 면적의 방향은 바깥 방향을 기준으로 한다.
\[\int_{\text{띠}}\vec{B} \cdot d\vec{a} = \oint \vec{B} \cdot (\vec{v} \times d\vec{l}) dt\] \[\frac{d\Phi}{dt} = \oint \vec{B} \cdot (\vec{v} \times d\vec{l})\]전하가 도선을 타고 움직이는 속도를 \(\vec{u}\)라고 하자. \(\vec{u}\)는 이미 도선에 전류가 흐르고있는 일반적인 상황까지 고려하기 위함이다. \(\vec{u}=\vec{0}\)이어도 무방하다. 전하의 속도 합은 \(\vec{w} = \vec{v} + \vec{u} \implies \vec{v} = \vec{w} - \vec{u}\)이고, 대입하면 \(\vec{u}\)는 \(d\vec{l}\)와 같은 방향이므로 사라진다.
\[= \oint \vec{B} \cdot (\vec{w} \times d\vec{l}) = \oint \vec{w} \cdot (d\vec{l} \times \vec{B})\] \[= \oint d\vec{l} \cdot (\vec{B} \times \vec{w}) = -\oint d\vec{l} \cdot (\vec{w} \times \vec{B})\] \[= - \oint \vec{f} \cdot d\vec{l} = -\varepsilon\] \[\therefore ~~ \varepsilon = - \frac{d\Phi}{dt}\]마이너스 기전력이 생긴다는 것은, 도선에 어느 방향으로 전류가 흐른다는 건가?
자기 선속의 방향을 기준으로 오른손 법칙을 적용했을 때, 감는 오른손 방향을 + 방향으로 정한다. 즉 자기 선속을 오른손으로 맞췄을 때 손가락과 반대 방향으로 전류가 발생한다. 이를 쉽게 생각하려면, 렌츠의 법칙 (Lenz’s law) 만 생각하면 된다.
\[\text{자연은 선속의 변화를 싫어한다.}\]즉, 선속이 감소하면 그것을 회복하고자 자기선속을 보강하는 방향으로 전류가 흐른다. 선속이 감소하면 +의 기전력이 생기고, 오른손의 감는 방향으로 전류가 흐른다. 선속이 증가하면 그것을 막고자 자기선속을 상쇄하는 방향으로 전류가 흐른다. 선속이 증가하면 -의 기전력이 생기고, 오른손의 감는 방향과 반대 방향으로 전류가 흐른다.
선속규칙 역설이 무엇인가?
선속 규칙은 사용할 때 주의할 점이 있다. 시간에 대한 선속 변화가 연속적일때만 적용 가능하다는 점이다.
위 그림에서 스위치를 a에서 b로 바꾸면 도선을 지나는 자기 선속은 2배가 되지만, 기전력은 생기지 않는다. 그 이유는, 선속 규칙의 유도 과정에서 \(\Phi(t)\)는 연속적이라고 가정하고 유도했기 때문이다. 만약 불연속적이라면, 도선 변화 띠에 해당하는 면적 자체가 존재하지 않을 수 있다.
\[d\Phi=\int_{\text{띠}}\vec{B} \cdot d\vec{a} = 0\]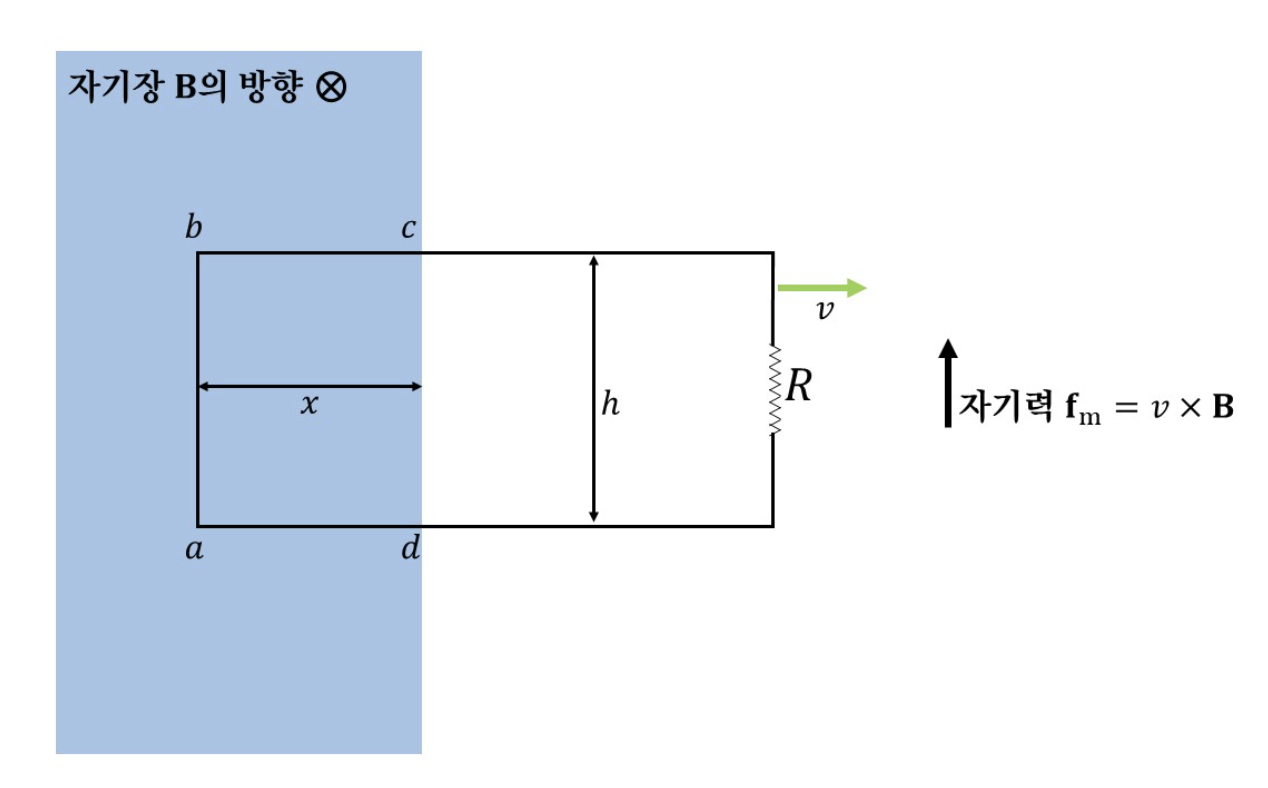
.jpg)
.jpg)