기초전자기학 7. 기전력이 무엇인가

기전력은 전류의 원인인가?

기전력이란, 전하를 분리시키는 능력이다. 단위는 볼트이며, 차원은 \(J / c\) 단위 전하당 에너지와 같다.

전하를 분리시키면 전기장이 만들어지고, 전위차가 생긴다. 전위차가 생기면 전하가 움직인다. 따라서 기전력은 전류의 원인으로 볼 수 있다.

전위차가 존재하면 전하가 이동하는건가?

전위란 Electric potential과 같다. 조건을 만족하는 시스템은 Potential이 낮은 상태(더 안정적인 상태)로 가려는 특징이 있다. 예를들어, 질량을 가진 물질은 중력 포텐셜이 높은 곳에서 낮은 곳으로 이동하려는 경향이 있다. 그 이유로 땅으로 떨어진다는 해석이 가능하다. 똑같이 전하를 가진 입자는 전기 포텐셜, 전위가 높은 곳에서 낮은 곳으로 이동하려는 경향이 존재한다. 중력 포텐셜을 만드는 근본적인 원인이 중력장이듯이, 전위를 만드는 근본적인 원인은 전기장이다.

기전력 정의의 의미가 무엇인가?

기전력의 정의는 다음과 같다.

\[\varepsilon \equiv \oint_{C} \vec{f} \cdot d\vec{l}\]

기전력은 닫힌 회로에 대해 단위 전하당 받는 힘을 길이에 대해 적분한 것이다. 이게 전하를 분리시키는 능력과 무슨 관련이 있는가 싶다. 하지만 위 식은 회로의 전위차를 정확히 캐치해내는 일반적인 방법이다.

만약 단위 전하당 받는 힘이 보존력만 존재한다면, 닫힌 회로에 대해 적분하면 0이 나온다. 예를들어, 전원이 없는 닫힌 회로는 전하들이 만드는 전기장만 존재하며 이는 보존장이다. 따라서 전하들이 움직이지 않는다.

만약 비보존력이 존재하면, 닫힌 회로에 대해 적분했을 때 보존력 성분은 상쇄되며 비보존력 항만 남는다. 따라서 기전력이 0이 아니게 된다. 비보존력이란 배터리와 같이 전하들을 인공적으로 분리해둔 힘과 같다. 이 힘이 바로 전하를 분리시키는 능력이다.

전원이란 무엇인가?

기전력을 만들어내는 물리적인 장치가 전원이다.

단위 전하당 힘이 무엇인가?

단위 전하당 힘 \(\vec{f} = \frac{\vec{F}}{q}\)이 무엇인가? 바로 전기장이다.

\[\vec{F} = q\vec{E} \implies \vec{E} = \frac{\vec{F}}{q}\]

그럼, 자기장도 단위 전하당 힘인가?

그렇지 않다. 자기장은 다음과 같다.

\[\vec{F} = q(\vec{v} \times \vec{B})\]

단위는 테슬라 \(T\) 를 사용하며, 움직이는 단위 전하에 수직으로 작용하는 힘이다.

기전력은 어떻게 계산하는가?

기전력의 정의를 사용하면 계산할 수 있다. 계산 방법은 회로 모양에 따라 다르다.

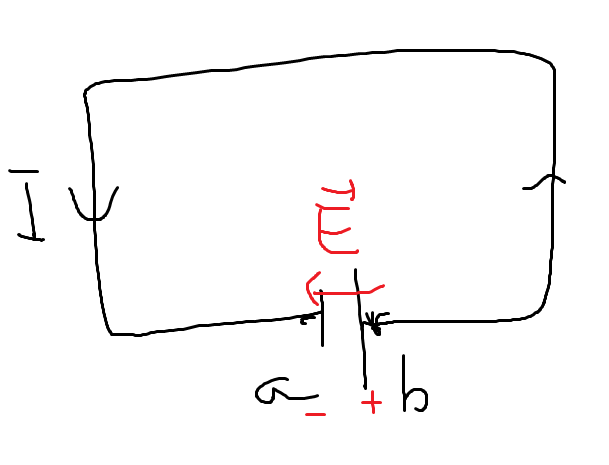
1. 배터리를 연결한 저항이 없는 회로

\(\vec{f_{o}}\)를 배터리 내의 전하를 분리시켜놓는 비보존력 (화학적인 힘), \(\vec{E}\)는 분리된 전하가 만드는 전기장이라고 하자. 전하가 받는 Total 힘은 다음과 같다.

\[\vec{f} = \vec{f_{o}} + \vec{E}\]

[!question] 단위 전하가 만드는 전기장은 고려하지 않는가?{title} 단위 전하가 만드는 전기장은 대부분 상쇄되거나, 미미한 영향을 미친다. 따라서 거시적인 경우 무시해도 좋다.

전기장은 폐곡선 적분하면 0이므로, \(a\)부터 \(b\)까지 \(\vec{f_{o}}\) 항만 적분에서 남게된다. \(\vec{f_{o}}\) 힘은 배터리 외부까지 영향을 미치지 않는다.

\[\varepsilon = \oint_{C} \vec{f} \cdot d\vec{l} = \int_{a}^{b} \vec{f_{o}} \cdot d\vec{l} + \oint_{C} \vec{E} \cdot d\vec{l} = \int_{a}^{b} \vec{f}_{o} \cdot d\vec{l}\]

배터리 내의 분리된 전하가 받는 알짜힘은 0이다. 따라서 \(0 = \vec{f}_{o} + \vec{E} \implies \vec{f}_{o} = -\vec{E}\)와 같다.

\[\varepsilon = \int_{a}^{b} \vec{f_{o}} \cdot d\vec{l} = -\int_{a}^{b} \vec{E} \cdot d\vec{l} = V(b)-V(a) = \Delta V\]

저항이 없는 이상적인 회로의 배터리를 연결하면, 기전력은 전위차와 같다.

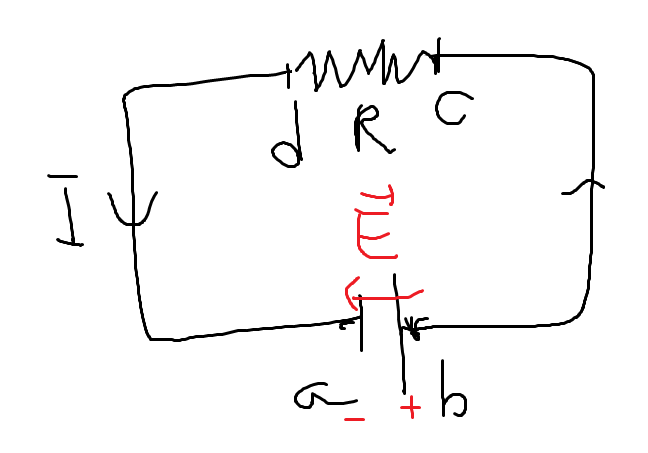
1. 배터리를 연결한 저항이 있는 회로

저항은 마찰과 같고, 마찰은 비보존력이다. 저항이 전하에 가하는 힘을 \(f_{f}\)라고 하면 total force는 다음과 같다.

\[\vec{f} = \vec{f_{o}} + \vec{E} + \vec{f_{f}}\]

기전력은 다음과 같다.

\[\varepsilon = \oint_{C} \vec{f} \cdot d\vec{l} = - \int_{a}^{b}\vec{E} \cdot d\vec{l} + \int_{c}^{d} \vec{f}_{f} \cdot d\vec{l} = \Delta V + \int_{c}^{d} \vec{f}_{f} \cdot d\vec{l}\]

\(\int_{c}^{d} \vec{f}_{f} \cdot d\vec{l}\)는 저항이 만드는 전위차와 같고, 저항이 만드는 전위차는 \(V=IR\)로 기술된다. \(V=IR\)의 해석은 다음과 같다.

• 저항 \(R\)에 전류 \(I\)를 흘리려면 \(V\)만큼의 전위차가 필요하다.
• 저항 \(R\)에 전류 \(I\)를 흘리려면 \(V\)만큼의 전위차를 극복해야 한다.

[!question] 왜 저항이 전위차를 만드는가?{title} 전자가 저항 물질을 통과하면서 포텐셜을 잃게 된다. 그로 인해 저항 시작단의 Potential보다 저항 끝단의 Potential이 더 작아진다. 따라서 저항이 전위차를 만든다.

따라서 기전력은 다음과 같다.

\[\varepsilon = \Delta V + IR\]