기초전자기학 6. 물질 속의 자기장

건국대학교 여준현 교수님의 전자기학1 수업을 정리한 내용입니다. 교재: Introduction to electrodynamics, David J. Griffths (4판)

Magnetic on Materials

물질에 자기장을 쏘면 어떻게 반응할까? 자성은 움직이는 전하가 만들어내고, 원자 수준에서 보면 전자가 핵 주위를 도는 것과 전자의 Spin이 미세 자성을 만들어낸다. 이것을 아주 작은 자기 쌍극자라고 생각하면, 원자는 무질서하게 배열되어있기 때문에 보통 미세 자기 쌍극자가 서로 상쇄된다. 하지만 자기장을 걸어주면 자기 쌍극자가 회전하면서 일렬로 배열된다. 이것이 나란하게 배열되면 상자성체(paramagnet), 반대로 배열되면 반자성체(diamagnet) 다. 몇몇은 자기장을 치워도 자성이 오랫동안 남아있는 강자성체(ferromagnet) 이기도 하다.

Forces and Torques on \(\vec{p}\)

1. \(\vec{\tau}_{\text{total}} = \vec{p} \times \vec{E}\)
2. \(\vec{E}\) is uniform : \(\vec{F}_{\text{total}} = \vec{0}\)
3. \(\vec{E}\) is not uniform : \(\vec{F}_{\text{total}} = \nabla(\vec{p} \cdot \vec{E})\)

Total Turque

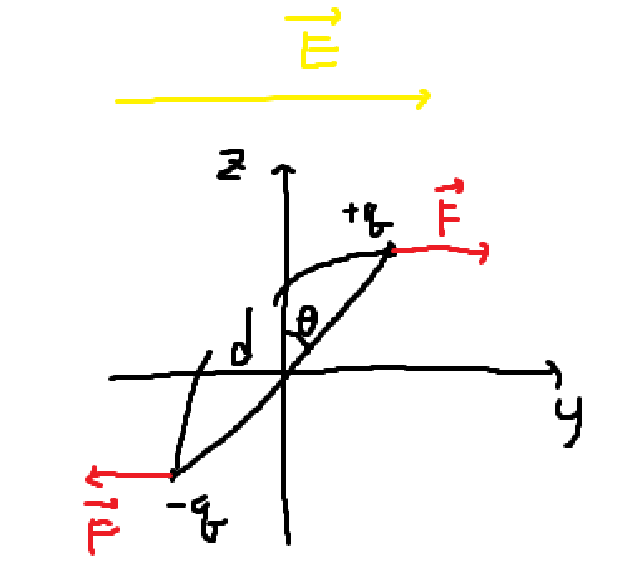
작은 쌍극자에 전기장을 걸면, 각 전하는 \(\vec{F}=q\vec{E}\)만큼 힘을 받는다. \(\vec{\tau} = \vec{r} \times \vec{F}\)이며, 총 토크의 크기는 \(\displaystyle \tau_{total} = 2rF\sin \theta = 2 \frac{d}{2} qE \sin \theta = qdE\sin \theta\)이다. 따라서 총 토크는 \(\vec{\tau}_{total} = \vec{p} \times \vec{E}\)로 셈할 수 있다.

Total Force on Uniform \(\vec{E}\)

\(\vec{E}\)가 균일하면, 두 힘 \(\vec{F}\)가 상쇄되어 알짜힘이 0이다. \(\vec{F}_{total}= 0\)

Total Force on Non-uniform \(\vec{E}\)

\(\vec{F}_{total} = q\vec{E}_{+} - q\vec{E}_{-} = q(\vec{E}_{+} - \vec{E}_{-}) = q(\vec{E}(\vec{r} + \vec{d}) - \vec{E}(\vec{r}))\)이다. 어떤 Field를 테일러 전개하면 \(\displaystyle f(\vec{r}) = f(\vec{r}_{0})+\left( dx \frac{\partial}{\partial x} + dy \frac{\partial}{\partial y} + \dots \right) f(\vec{r}) \mid_{\vec{r}=\vec{r}_{0}}+\dots = f(\vec{r}_{0})+\left( d\vec{r} \cdot \nabla \right) f(\vec{r})\mid_{\vec{r}=\vec{r}_{0}}+\dots\) 이고, 이를 통해 함수의 변화량은 다음과 같다.

\[\Delta f(\vec{r}) = f(\vec{r}+d\vec{r})-f(\vec{r}) \simeq (d\vec{r} \cdot \nabla)f(\vec{r})\]

따라서 두 전기장의 차이는 \(\vec{d}\)가 아주 작으므로 \(\vec{E}(\vec{r}+ \vec{d}) - \vec{E}(\vec{r}) \simeq (\vec{d} \cdot \nabla)\vec{E}(\vec{r})\)로 근사될 수 있다. \(\vec{F}_{\text{total}} = q(\vec{d} \cdot \nabla)\vec{E} = (\vec{p} \cdot \nabla)\vec{E}\) Consider \(\nabla(\vec{p} \cdot \vec{E}) = (\vec{E} \cdot \nabla)\vec{p} + (\vec{p} \cdot \nabla)\vec{E} + \vec{E} \times (\nabla \times \vec{p}) + \vec{p} \times (\nabla \times \vec{E})\)인데, \(\vec{p}\)는 상수벡터이므로 \(\vec{p}\)를 미분하는 항은 모조리 날아간다. 또, \(\nabla \times \vec{E} = 0\)이므로 \(\nabla(\vec{p} \cdot \vec{E}) = (\vec{p} \cdot \nabla)\vec{E}\)만 남게된다. 따라서 전기장이 작은 쌍극자에게 가하는 총 알짜힘은 \(\vec{F}_{total}= \nabla(\vec{p} \cdot \vec{E})\)로 기술된다.

Forces and Torques on \(\vec{m}\)

1. \(\vec{\tau}_{total} = \vec{m} \cdot \vec{B}\)
2. \(\vec{B}\) is uniform : \(\vec{F}_{total} = \vec{0}\)
3. \(\vec{B}\) is not uniform : \(\vec{F}_{total} = \nabla(\vec{m} \cdot \vec{B})\)

자기 쌍극자와 자기장이 만날 때 어떻게 회전되는지 셈하는 것이 기본이다. 전류가 흐르는 작은 네모꼴 고리부터 시작한다. 일반적인 고리의 경우는 아주 작은 네모꼴 고리를 겹쳐서 ‘안쪽’ 변을 지워서 만들 수 있으므로, 일반성을 잃지 않는다.

Total Torque

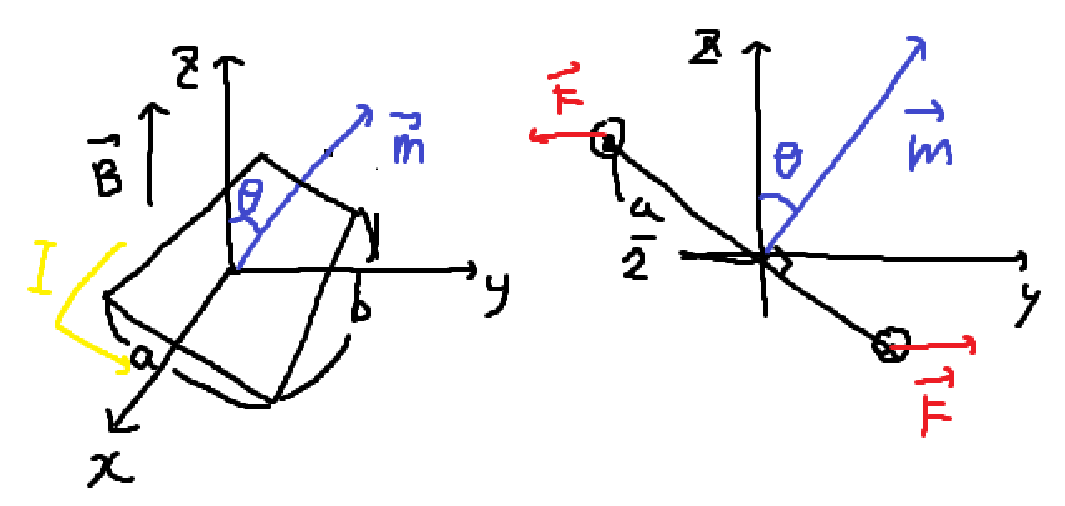
고리 중심을 원점으로 하고, 자기장 방향을 \(\vec{B} = B \hat{z}\)로 하도록 좌표계를 설정하자. 이때 전류 고리가 받는 힘은 \(dq\)가 받는 힘의 합이다. 고리의 경로를 C라고 하면, \(\displaystyle\vec{F}_{m}=\oint_{C} dq (\vec{v} \times \vec{B})\). \(dq=\lambda dl\), \(I = \lambda v\)이므로 \(\displaystyle \vec{F}_{m} = \oint_{C} \lambda dl (\vec{v} \times \vec{B}) = \oint_{C}I(d\vec{l} \times \vec{B})\)이다. 길이가 a인 경로의 \(d\vec{l}\)와 \(\vec{B}\)를 오른손 법칙써서 힘의 방향을 계산해보면, 서로 +x 방향과 -x방향으로 잡아 당기기만 하고 회전에는 영향을 주지 않는다. 길이가 b인 경로의 \(d\vec{l}\)와 \(\vec{B}\)의 힘의 방향을 계산해보면 2번 그림과 같고, 저 힘으로 인해 Torque가 생긴다. \(\vec{\tau} = \vec{r} \times \vec{F}\)이므로, 총 Torque의 크기는 \(\displaystyle \tau_{total} = 2 \cdot \frac{a}{2} F\sin \theta\). \(F=Id\vec{l} \times \vec{B} = IbB\)와 같다. \(d\vec{l}\)와 \(\vec{B}\)는 수직이므로 \(\sin \alpha=1\)이다.

\[\tau_{total} = IabB\sin \theta \implies \vec{\tau} = \vec{m} \times \vec{B}\]

Total Force on Uniform \(\vec{B}\)

\(\displaystyle \vec{F}_{total} = I \oint_{C}(d\vec{l} \times \vec{B})\)인데, B가 균일하므로 적분에 포함되지 않는다. \(\displaystyle =I (\oint_{C} d \vec{l})\times \vec{B}\), \(\displaystyle \oint_{C} d \vec{l} = 0\)이므로 알짜힘이 0이다.

Total Force on Non-uniform \(\vec{B}\)

\(\displaystyle\vec{F}_{total} = I \oint_{C} d\vec{l} \times \vec{B}(\vec{r})\), \(\vec{r}\)이 작으므로 \(\vec{B}(\vec{r})\)를 테일러 전개할 수 있다.

\[\vec{B}(\vec{r}) \simeq \vec{B}(\vec{r}_{0}) + ((\vec{r}-\vec{r}_{0}) \cdot \nabla)\vec{B}(\vec{r})\mid_{\vec{r}=\vec{r}_{0}}\]

이 결과를 대입하면 \(\displaystyle I \oint_{C} d\vec{l} \times (\vec{B}(\vec{r}_{0}) + ((\vec{r} - \vec{r}_{0} ) \cdot \nabla) \vec{B}(\vec{r})\mid_{\vec{r}=\vec{r}_{0}})\)이다. 같은 논리로 \(\vec{B}(\vec{r}_{0})\)과 \(\vec{r}_{0}\) 항은 적분범위에 포함되지 않아 밖으로 빠지면 적분 결과가 0이다.

\[\vec{F} = I \oint_{C} d\vec{l} \times (\vec{r} \cdot \nabla)\vec{B}(\vec{r})\mid_{\vec{r}=\vec{r}_{0}}\]

\(\displaystyle F_{i} = I \sum_{j,k} \epsilon_{ijk} \oint_{C} dl_{j} (\vec{r} \cdot \nabla)B_{k}(\vec{r})\mid_{\vec{r}=\vec{r}_{0}} = I \sum_{j,k} \epsilon_{ijk}\oint_{C} dl_{j} \sum_{l}x_{l}\partial_{l}B_{k}(\vec{r})\mid_{\vec{r}=\vec{r}_{0}}\)이고, \(\partial_{l}B_{k}(\vec{r})\mid_{\vec{r}=\vec{r}_{0}}\)은 최종적으로 어떤 상수벡터가 될 것이므로, \(\vec{c}\)로 치환하여 생각한다.

\[F_{i} = I \sum_{j,k} \epsilon_{ijk} \oint_{C} dl_{j} \sum_{l} x_{l}c_{l} = I\sum_{j,k} \epsilon_{ijk} \oint_{C} dl_{j} (\vec{r} \cdot \vec{c})\]

적분 항인 \(\displaystyle \oint_{C} d\vec{l}(\vec{r} \cdot \vec{c})\)는 마치 (\(\vec{c} \cdot f\)) 꼴과 비슷하다. 여기서는 약간 테크닉이 필요한데, 다음을 생각해보자.

\[\nabla \times (\vec{c} f) = -\vec{c} \times \nabla f\] \[\implies \nabla \times (\vec{c} f) \cdot d\vec{a} = -\vec{c} \times \nabla f \cdot d\vec{a} = - \nabla f \times d\vec{a} \cdot \vec{c}\] \[\implies \int_{S} \nabla \times (\vec{c} f) \cdot d\vec{a} = - \int_{S} \nabla f \times d \vec{a} \cdot \vec{c}\] \[\implies \oint_{\partial S} \vec{c} f \cdot d \vec{l} = \vec{c} \cdot \oint_{\partial S} f d\vec{l} = - \int_{S} \nabla f \times d\vec{a} \cdot \vec{c}\] \[\implies \oint_{\partial S} f d\vec{l} = - \int_{S} \nabla f \times d \vec{a}\]

이 결과를 그대로 \(I\displaystyle \oint_{C}(\vec{r} \cdot \vec{c}) d\vec{l}\)에 적용하면, \(\displaystyle = -I \int_{S} \nabla(\vec{r} \cdot \vec{c}) \times d \vec{a}\)이고, \(\nabla(\vec{r} \cdot \vec{c})\)에서 \(\vec{c}\)는 미분에 영향을 끼치지 않고 \(\vec{r}\)를 \(\nabla\)로 미분하면 그냥 \((1,1,1)\)이다. 따라서 \(\nabla(\vec{r} \cdot \vec{c}) = \vec{c}\)임.

\[-I \int_{S} \vec{c} \times d\vec{a} = -I\vec{c} \times \int_{S} d\vec{a} = \vec{m} \times \vec{c}\]

따라서…

\[F_{i} = \sum_{j,k} \epsilon_{ijk} I\oint_{C} dl_{j} (\vec{r} \cdot \vec{c})\] \[= \sum_{j,k}\epsilon_{ijk}(\vec{m} \times \nabla B_{k}(\vec{r})\mid_{\vec{r}=\vec{r}_{0}})_{j} = \sum_{j,k} \epsilon_{ijk} \sum_{p,q}\epsilon_{jpq} m_{p}\partial_{q}B_{k}(\vec{r})\mid_{\vec{r}=\vec{r}_{0}}\] \[= - \sum_{k,p,q}(\delta_{ip}\delta_{kq} - \delta_{iq}\delta_{kp})m_{p}\partial_{q}B_{k} = \sum_{k}(m_{k}\partial_{i}B_{k} - m_{i}\partial_{k}B_{k}) = \partial_{i}(\vec{m} \cdot \vec{B}) - m_{i} \nabla \cdot \vec{B}\]

이때 \(\nabla \cdot \vec{B} = 0\)이므로, \(\vec{F}_{total} = \nabla(\vec{m} \cdot \vec{B})\)만 남는다.

Coordinate Freedom

좌표계의 의존성을 없앤 Dipole 전위와 전기장의 표기법을 알아보자. 먼저 전위는 다음과 같다. \(\displaystyle V_{dip} = \frac{1}{4\pi\epsilon_{0}} \frac{1}{r^2} \vec{P} \cdot \hat{r}\). 전기장은 \(\displaystyle E_{i}= - \frac{{\partial V}}{\partial x_{i}}\)이므로 대입하면, 다음과 같다.

\[\displaystyle E_{i}= - \frac{1}{4\pi\epsilon_{0}} \frac{\partial}{\partial x_{i}} \left( \frac{{\vec{P} \cdot \hat{r}}}{r^2} \right) = - \frac{1}{4\pi\epsilon_{0}} \frac{\partial}{\partial x_{i}} \left( \frac{\sum_{j}P_{j}x_{j}}{r^3} \right)\]

이때 중요한 꿀팁! \(\displaystyle \frac{\partial}{\partial x_{i}}x_{j} = \delta_{ij}\)와 같다. 따라서

\[E_{i} = -\frac{1}{4\pi\epsilon_{0}} \sum_{j} \left( \frac{P_{j}\delta_{ij}}{r^3} - (P_{j}x_{j}) \frac{3x_{i}}{r^5} \right) = -\frac{1}{4\pi\epsilon_{0}} \left( \frac{P_{i}}{r^3} - \frac{3(\vec{P} \cdot \vec{r})x_{i}}{r^5} \right)\]

따라서, \(\displaystyle \vec{E}_{dip} = \frac{1}{4\pi\epsilon_{0}} \frac{1}{r^3}(3(\vec{P} \cdot \hat{r})\hat{r} - \vec{P})\)로 좌표계에 의존하지 않는 표현식으로 Dipole 전기장을 기술한다.

Potential Energy by \(\vec{m}, \vec{B}\)

\(\vec{F} = \nabla(\vec{m} \cdot \vec{B})\)이고, \(\vec{F}\)는 \(\vec{F}=\nabla f\)꼴을 만족하므로 보존장이다. 따라서 \(U=-\vec{m} \cdot \vec{B}\)로 정의하면, \(\vec{m}\)와 \(\vec{B}\)가 평행할 때 \(\vec{m} \cdot \vec{B}\)가 가장 크다. 따라서 U가 가장 작다. 반대로 \(\vec{m}\)과 \(\vec{B}\)가 서로 수직하면 U가 가장 크다. 이는 자기장 \(\vec{B}\)가 걸리면 \(\vec{m}\)이 B 방향으로 정렬하는게 에너지적으로 안정적이라는 물리적 해석을 할 수 있다.

만약 쌍극자 \(\vec{p}_{1}, \vec{p}_{2}\)가 있을 때 \(U\)를 구하고 싶다면, 먼저 쌍극자 하나가 만드는 전기장을 생각하고, 그 전기장 위에 다른 쌍극자를 올리는 상황으로 해석하면 된다. \(\displaystyle \vec{E}(\vec{r}) = \frac{1}{4\pi\epsilon_{0}} \frac{1}{r^3}(3(\vec{p_{1}} \cdot \hat{r})\hat{r} - \vec{p_{1}})\)이므로, \(\displaystyle U=-\vec{p}_{2} \cdot \vec{E} = \frac{1}{4\pi\epsilon_{0}} \frac{1}{r^3}(\vec{p_{1}}\cdot \vec{p}_{2} -3(\vec{p_{1}} \cdot \hat{r})\hat{r}\cdot \vec{p}_{2})\)를 계산하면 된다.

자화된 물체가 만드는 자기장

\(\displaystyle \vec{M}(\vec{r}') = \frac{d\vec{m}}{d^3\vec{r}'}\), \(\vec{K}_{b}(\vec{r}') = \vec{M} \times \hat{n}\), \(\vec{J}_{b}(\vec{r}') = \nabla \times \vec{M}\), 자화된 물체가 만드는 장은 \(\vec{K}_{b}\)와 \(\vec{J}_{b}\)가 만드는 장과 같다.

\[\displaystyle \vec{A}= \frac{\mu_{0}}{4\pi} \oint_{S} \frac{\vec{K}_{b}}{\eta} da' + \frac{\mu_{0}}{4\pi} \int_{V} \frac{\vec{J}_{b}}{\eta}d^3\vec{r}'\]

유도

Magnetic Dipole moment는 \(\displaystyle \vec{m} = I \int_{S} d\vec{a}'\)로 정의되고, \(d\vec{m}\)는 미소 체적 \(d^3\vec{r}'\) 안의 \(\vec{m}\)의 평균으로 정의한다. 자화 밀도 Magnetization은 \(\displaystyle\vec{M}(\vec{r}') = \frac{d\vec{m}}{d^3\vec{r}'}\)로 정의한다.

자기 쌍극자 모멘트 하나가 만드는 전위는 \(\displaystyle\vec{A}_{dip} = \frac{\mu_{0}}{4\pi} \frac{1}{\eta^2} \vec{m} \times \hat{\eta}\)와 같다. 만약 연속적으로 분포한 자기 쌍극자 모멘트가 만드는 전위는 미소 자기 쌍극자 \(d\vec{m}\)가 만드는 전위의 합과 같다.

\[\vec{A} = \frac{\mu_{0}}{4\pi} \int_{V} d\vec{m} \times \frac{\hat{\eta}}{{\eta^2}} = \frac{\mu_{0}}{4\pi} \int_{V} d^3\vec{r}' \vec{M} \times \frac{\hat{\eta}}{\eta^2}\]

\(\displaystyle\frac{\hat{\eta}}{\eta^2} = \nabla'\left( \frac{1}{\eta} \right)\)이므로 \(\displaystyle \vec{A} = \frac{\mu_{0}}{4\pi} d^3\vec{r}' \vec{M} \times \nabla'\left( \frac{1}{\eta} \right)\)와 같이 쓸 수 있다. \(\nabla \times (f\vec{A}) = (\nabla f) \times \vec{A} + f(\nabla \times \vec{A}) \implies \vec{A} \times (\nabla f) = - \nabla \times (f\vec{A}) + f(\nabla \times \vec{A})\)이므로, 다음과 같다.

\[\vec{A} = \frac{\mu_{0}}{4\pi} \int_{V}d^3\vec{r}'\left( -\nabla' \times \left( \frac{1}{\eta}\vec{M} \right) + \frac{1}{\eta}(\nabla \times \vec{M}) \right)\]

[!tip]- Gauss’ Theorem의 따름 정리 : \(\int_{V} d^3\vec{r} (\nabla \times \vec{B}) = - \oint_{\partial V} \vec{B} \times d \vec{a}\){title} \(\vec{c} = const\)일 때 \(\vec{A} = \vec{B} \times \vec{c}\)를 가정하자.

\[\nabla \cdot \vec{A} = \nabla \cdot (\vec{B} \times \vec{c}) = \sum_{i} \partial_{i} (\vec{B} \times \vec{c})_{i}\] \[= \sum_{i} \partial_{i}\sum_{j,k}\epsilon_{ijk}B_{j}c_{k}=\sum_{i,j,k}c_{k}\epsilon_{kij}\partial_{i}B_{j}=\vec{c} \cdot (\nabla \times \vec{B})\] \[\int d^3\vec{r} (\nabla \cdot \vec{A}) = \oint \vec{A} \cdot d\vec{a} =\oint (\vec{B} \times \vec{c}) \cdot d\vec{a}\] \[= \oint(d\vec{a} \times \vec{B}) \cdot \vec{c} = \vec{c} \cdot \int d^3\vec{r}(\nabla \times \vec{B})\] \[\therefore ~ \int d^3\vec{r}(\nabla \times \vec{B}) = -\oint(\vec{B} \times d\vec{a})\]

위 따름 정리를 사용하면, \(\displaystyle \int_{V} d^3\vec{r}'\left( -\nabla' \times \left( \frac{1}{\eta}\vec{M} \right) \right) = \oint_{\partial V} \frac{1}{\eta}\vec{M} \times d\vec{a} = \oint_{\partial V} \frac{1}{\eta} \vec{M} \cdot \hat{n} da\)와 같다. \(\vec{A}\)를 다시 쓰면, \(\displaystyle \vec{A} = \frac{\mu_{0}}{4\pi} \oint_{\partial V} \frac{1}{\eta} \vec{M} \cdot \hat{n} da + \frac{\mu_{0}}{4\pi} \int_{V} \frac{1}{\eta} (\nabla \times \vec{M}) d^3\vec{r}'\)이고, 이 모양은 우리가 기존의 알던 벡터 포텐셜의 일반식 \(\displaystyle \vec{A} = \frac{\mu_{0}}{4\pi} \int_{V} \frac{\vec{J}(\vec{r}')}{\eta}d^3\vec{r}' = \frac{\mu_{0}}{4\pi} \int_{S} \frac{\vec{K}(\vec{r}')}\eta da'\)와 같다. \(\vec{M} \cdot \hat{n}\)가 \(\vec{K}\)에 대응되고, \(\nabla \times \vec{M}\)가 \(\vec{J}\)에 대응되고 있다. 따라서 자화로 인해 생기는 Current Density를 각각 \(\vec{J}_{b}(\vec{r}') = \nabla \times \vec{M}\), \(\vec{K}_{b}(\vec{r}') = \vec{M} \cdot \hat{n}\)라고 정의한다. 이는 편극된 유전체가 만드는 전하 밀도 \(\rho_{b}(\vec{r}') = - \nabla \cdot \vec{P}\), \(\sigma_{b}(\vec{r}') = \vec{P} \cdot \hat{n}\)와 비슷하다.

Magnetic Field \(\vec{H}\)

자화된 Material의 Current 밀도 \(\vec{J}\)는 자유 전하가 만드는 \(\vec{J}_{f}\)와 자화되어 생기는 성분인 \(\vec{J}_{b}\) 두 항이 존재한다. 이를 통해 Ampare’s law를 다시 표현하면 \(\nabla \times \vec{B} = \mu_{0}\vec{J} \implies \frac{1}{\mu_{0}} \nabla \times \vec{B} = \vec{J}_{f} + \vec{J}_{b}\) \(= \vec{J}_{f} + \nabla \times \vec{M} \implies \nabla \times \left( \frac{1}{\mu_{0}} \vec{B} - \vec{M}\right) = \vec{J}_{f}\)이고, \(\displaystyle \vec{H} \equiv \frac{1}{\mu_{0}}\vec{B} - \vec{M}\)로 정의한다. \(\vec{H}\)는 따로 이름이 있지 않고, 그냥 Magnetic Field라고 불린다.

\[\displaystyle \nabla \times \vec{H} = \vec{J}_{f} \implies \oint \vec{H} \cdot d\vec{l} = I_{free, inside}\]