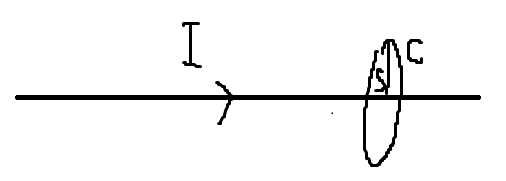기초전자기학 5. 정자기학
건국대학교 여준현 교수님의 전자기학1 수업을 정리한 내용입니다. 교재: Introduction to electrodynamics, David J. Griffths (4판)
Current
전류(Current)란 도선의 한 지점을 단위 시간동안 지나가는 전하량으로 정의한다. 만약 도선이 아주 얇은 1차원이라면, 전하의 이동 방향은 + 또는 -로 표기할 수 있다. 따라서 \(\displaystyle I=\frac{dq}{dt}\)는 1차원 상황에서 방향이 고정된 ‘특수한 상황’ 한에서 전하가 흐르는 세기와 방향을 모두 고려한다. 하지만, 일반적인 경우 한 지점을 지나는 전하는 흐르는 방향이 + 또는 -로만 표현되지 않는다. 전류는 전하의 속도 \(\vec{v}\)와 평행하다. \(\displaystyle \vec{I} = \frac{dq}{dt} \hat{v}\), 이때 \(dq=\lambda dl\), \(dl = vdt\)임을 이용하여 \(\displaystyle \vec{I} = \frac{\lambda dl}{dt} \hat{v} = \frac{{\lambda vdt}}{dt}\hat{v} = \lambda \vec{v}\)라는 사실을 얻어낸다. 정리하면, Current는 1차원 Line을 타고 흐르는 전하를 나타내는 물리량이라고 보면 된다.
Current Density
Current는 단순히 1차원이 아닌 2차원 표면이나 3차원 부피를 통해 흐르는 경우가 더 일반적이다. 이를 각각 \(\displaystyle \vec{K}\equiv \frac{d\vec{I}}{dl_{\bot}}\), \(\displaystyle \vec{J} \equiv \frac{d\vec{I}}{da_{\bot}}\)로 정의한다. \(\vec{K}\)는 Surface 위에서 연속 전류 분포를 의미하는 양이고, Surface Current Density라고 부른다. \(\vec{J}\)는 Volume 내에서 연속 전류 분포를 의미하는 양이고, Volume Current Density라고 부른다. 이는 마치 Electricstatics에서 연속 전하 분포를 \(q\)가 아닌 \(dq\)를 단위로 총 전하량을 단위 전하 \(dq\)를 모두 Sum하는 방식으로 계산하는 것과 같다.
\[Q_{total}=\int dq = \int_{C}\lambda dl = \int_{S}\sigma da = \int_{V}\rho d\tau\]똑같이 어떤 선분, 어떤 면적을 수직으로 쓸고 지나가는 총 전류 \(I\)는 단위 전류 \(dI\)를 Sum하여 계산할 수 있다. 어떤 지점을 쓸고 지나가는 전류는 그냥 \(I=\lambda v\)이므로 고려하지 않는다. \(\displaystyle I_{total} =\int dI = \int \vec{K} \cdot d\vec{l} = \int_{S} \vec{J} \cdot d\vec{a}\) 와 같다. \(\vec{K}\)와 \(\vec{J}\)가 어떤 길이, 면적에 대해 ‘수직한 성분’만을 취하기 위해 내적을 사용한다.
Lorentz Force Law
움직이는 전하 \(q\)가 자기장에 의해 받는 힘은 \(\vec{F}_{m} = q\vec{v} \times \vec{B}\)이다. 이는 실험을 통해 밝혀낸 값이다. 만약 자기장 + 전기장이 같이 있다면, 전하 \(q\)는 \(\vec{F} = q(\vec{E} + \vec{v} \times \vec{B})\) 힘을 받게 된다.
전류 \(I\)가 흐르는 도선이 자기장에 의해 받는 힘은, 도선 내 단위 전하 \(dq\)가 받는 힘을 모두 합하면 된다. 이때 \(dq = \lambda dl\)이고, \(dl\)은 전하가 움직이는 속도 \(v\)를 사용하면 \(dl=vdt\)와 같다. 이 사실을 통해 도선에 흐르는 전류 \(I\)는 \(I=\lambda v\)와 같다. \(\displaystyle \vec{F}_{m} = \int \vec{v} \times \vec{B} dq = \int \vec{v} \times \vec{B} \lambda dl = \int d\vec{l} \times \vec{B} \lambda v = I \int d\vec{l} \times \vec{B}\) 또는 \(\displaystyle \vec{F}_{m} = \int \vec{I} \times \vec{B} dl\)로 표기 가능. \(\vec{v}\)와 \(d\vec{l}\)의 위치를 바꿀 수 있는 이유는 두 벡터의 방향이 같기 때문이다. 벡터곱의 스칼라 양은 밖으로 뺄 수 있으므로, \(\vec{v} \times \vec{B} \lambda d l = \hat{v} \times \vec{B} \lambda v dl = d \vec{l} \times \vec{B} \lambda v\)와 같다.
연속적인 Current가 일정한 방향을 가지고 Surface 위에서 흐르고 있을 때, Surface가 자기장에 의해 받는 힘은 Surface 내 단위 Current \(d\vec{I}\)가 받는 힘을 모두 합하면 된다. \(\displaystyle \vec{F}_{m}=\int dI \int d\vec{l} \times \vec{B} = \iint d\vec{I} \times \vec{B} dl\)이고, \(d\vec{I} = \vec{K} d l_{\bot}\)이므로, \(\displaystyle \vec{F}_{m}=\iint_{S} \vec{K} \times \vec{B} dldl_{\bot} = \iint_{S} \vec{K} \times \vec{B} da\)로 계산 가능하다.
연속적인 Current가 일정한 방향을 가지고 Volume 위에서 흐르고 있을 때, Volume이 자기장에 의해 받는 힘 또한 단위 Current \(d\vec{I}\)가 받는 힘을 모두 합하면 된다. \(\displaystyle \vec{F}_{m} = \iint d\vec{I} \times \vec{B} dl\)이고, \(d\vec{I} = \vec{J} d a_{\bot}\)이므로, \(\displaystyle \vec{F}_{m} = \iiint_{V} \vec{J} \times \vec{B} d\tau\)로 계산 가능하다.
보면, \(\displaystyle \vec{F}_{m}=\int \vec{I} \times \vec{B} dl = \int \vec{K} \times \vec{B} da = \int \vec{J} \times \vec{B} d\tau\)로 일관성이 있다. 전류와 길이의 곱은 \(\vec{I} dl = \vec{K} da = \vec{J} d\tau\)로 사실 \(\vec{K}, \vec{J}\)가 무엇인지 생각해보면 당연하다.
자기력이 전하에 하는 일
자기력은 일을 하지 않는다. 계산해보면, \(\displaystyle W = \int_{C} \vec{F}_{m} \cdot d\vec{l} = \int_{C} q(\vec{v} \times \vec{B}) \cdot d\vec{l} = \int_{C} q(\vec{v} \times \vec{B}) \cdot \vec{v} dt = 0\). \(\vec{v} \times \vec{B}\)는 \(\vec{v}\)와 수직이므로, 내적하면 0이기 때문에다. 하지만 전하가 움직일 때 자기장은 전하에 힘을 가하지 않는가? 왜 하는 일이 0인지 직관적으로 이해가 되지는 않지만, 실제로 하는 일은 0이다.
Continuity Equation
어떤 일반적인 폐곡면 S를 뚫고 나오거나 들어가는 Total Current 양을 계산해보자. 닫힌 면적 S를 수직으로 쓸고 지나가는 총 전류 (Flux)의 양는 \(\displaystyle I = \oint_{S} \vec{J} \cdot d\vec{a}\)로 계산할 수 있다. Gauss’ Theorem을 사용하면 \(\displaystyle \oint_{S} \vec{J} \cdot d\vec{a} = \int_{V} \nabla \cdot \vec{J} d\tau\)와 같다. 저것의 물리적인 의미는, V를 뚫고 나가는 총 Charge의 양과 같다. Total Charge는 \(\rho\)를 Volume에 대해 체적적분하면 된다. Total Charge가 시간에 따라 감소하는 변화량이므로, \(\displaystyle - \frac{d}{dt}\int_{V} \rho d\tau\)와 같다. 따라서 \(\displaystyle \int_{V} \nabla \cdot \vec{J} d\tau = - \int_{V} \frac{d \rho}{dt}d\tau \implies \nabla \cdot \vec{J} = - \frac{{\partial \rho}}{\partial t}\) 결과를 얻는다. 이것은 어떤 체적 V에서 전하가 빠져나가는 만큼 부피 내의 전하가 줄어든다는 전하 보존 법칙을 정확히 설명한다.
Steady Current
Steady Current란, 전하가 늘거나 줄지 않고, 진로도 바뀌지 않고, 영원히 계속되는 전하의 흐름을 뜻한다. 즉 \(\vec{J}\)가 Steady Current면 \(\displaystyle \frac{{\partial \vec{J}}}{\partial t} = 0\)가 성립한다. 이는 마치 Electricstatics에서 움직이지 않는 전하, \(\displaystyle \frac{{\partial \rho}}{\partial t}=0\)인 상황만을 고려한 것과 같다. Steady Current를 연구하는 이론이 바로 Magnetostatics이고, 후술할 내용은 Magnetostatics에 대한 것이다. \(\vec{J}\)가 Steady Current라면, 위의 연속방정식 결과는 \(\nabla \cdot \vec{J} = 0\)이다.
Biot-Savart law
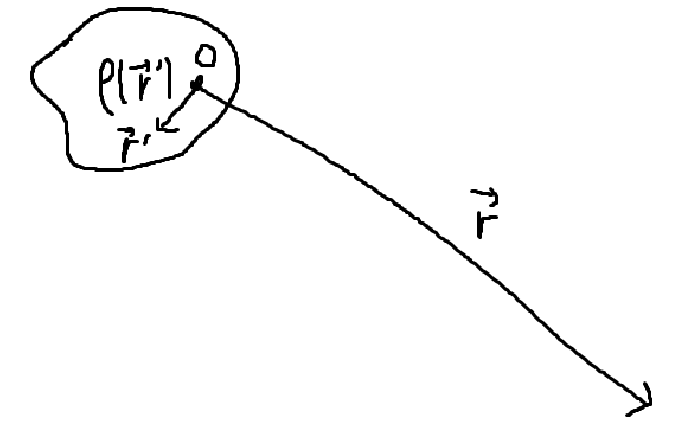
이제 핵심은 자기장 \(\vec{B}\)를 구하는 것이다. 우리의 목표는 Steady Current가 만드는 자기장 \(\vec{B}\)를 구하는 것이다. (Steady Current가 아닌 경우 사용할 수 없다.) 전기장 \(\vec{E}\)의 경우 점전하 q가 만드는 전기장은 \(\displaystyle \vec{E}(\vec{r})= \frac{1}{4\pi \epsilon_{0}} \frac{q}{r^2} \hat{r}\)였고, 연속적인 전하 분포를 고려하여 q 대신 \(dq\)를 사용하고 중첩 원리에 의해 \(dq\)가 만드는 전기장을 모두 더함으로써 일반적인 전기장 \(\displaystyle \vec{E}(\vec{r})=\frac{1}{4\pi\epsilon_{0}} \int dq \frac{\hat{\eta}}{\eta^2}\) 식을 유도해낼 수 있었다.
하지만 자기장의 경우 위와 같은 논리를 사용할 수 없다. 단일 점전하 하나만 움직이는 경우 Steady Current를 만들 수 없기 때문이다. 자기장의 최소 단위는 도선이다. 어떤 곡선 C에서 Steady Current가 흐를 때 도선이 만들어내는 자기장은 \(\displaystyle \vec{B}(\vec{r}) = \frac{\mu_{0}}{4\pi} \int_{C} \frac{\vec{I} \times \hat{\eta}}{\eta^2}dl'\)이라고 실험을 통해 밝혀냈다. \(I\)와 \(dl'\)을 바꾸면 \(\displaystyle \vec{B}(\vec{r}) = \frac{\mu_{0}}{4\pi} I \int_{C} \frac{d\vec{l}' \times \hat{\eta}}{\eta^2}\)로 표현할 수 있다. 이때 \(d\vec{l}'\)는 도선의 방향이다. 자기장의 단위는 로런츠 법칙으로 차원분석 해보면 \(N / (A \cdot m)\)이고, 이를 테슬라(tesla) T라고 정의한다.
(전류 x 길이)는 \(\vec{I} dl \iff \vec{K} da \iff \vec{J} d\tau\)와 같으므로, \(\displaystyle \vec{B}(\vec{r}) = \frac{\mu_{0}}{4\pi} \iint_{S} \frac{\vec{K}(\vec{r}') \times \hat{\eta}}{\eta^2}da'\), \(\displaystyle \vec{B}(\vec{r}) = \frac{\mu_{0}}{4\pi} \iiint_{V} \frac{\vec{J}(\vec{r}') \times \hat{\eta}}{\eta^2}d\tau'\)임을 알 수 있다. 각각 어떤 곡면 S에 Steady Current가 흐를 때, 어떤 체적 V에 Steady Current가 흐를 때 곡면, 체적이 만드는 자기장을 구하는 식이다.
자기장의 발산과 회전 (Ampere’s law)
핵심 : \(\nabla \cdot \vec{B} = 0\), \(\nabla \times \vec{B} = \mu_{0}\vec{J}\)
전기장의 발산과 회전을 셈하면 각각 \(\displaystyle \nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}}\), \(\nabla \times \vec{E} = 0\)이라는 중요한 성질이 있어, 이를 통해 전기장을 더 쉽게 계산해낼 수 있었다. 자기장도 현재 비오-사바르 법칙으로 적분하여 구하는 것은 너무 복잡하기 때문에, \(\nabla \cdot \vec{B}\), \(\nabla \times \vec{B}\)를 셈하여 더 쉽게 계산해내는 방법을 찾아야 한다.
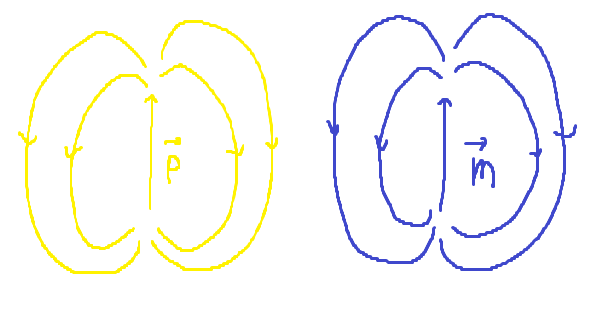
결론을 말하자면, \(\nabla \cdot \vec{B} = 0\), \(\nabla \times \vec{B} = \mu _0 \vec{J}(\vec{r})\)이다. 특히 두번째 결과를 Ampere’s law (앙페르의 법칙) 이라 부른다. 앞의 결과를 적분꼴로 바꾸면 \(\displaystyle \int_{V} \nabla \cdot \vec{B} d\tau = \oint_{S} \vec{B} \cdot d \vec{a} = 0\). 즉, 자기장을 만드는 Magnetic Source를 감싸는 닫힌 곡면 S를 정의하면, 자기장은 그 곡면을 뚫고 쭉 뻗어나가지 않는다는 것을 의미한다. 자기장은 곡면을 뚫고 나가는만큼 다시 Source로 돌아오는 Field 모양이며, 이는 Dipole Field 모양과 동일하다. Magnetic Source의 최소 단위는 Dipole부터 시작하며, Monopole 자기장이 없다.
앙페르의 법칙을 적분꼴로 바꾸면, \(\displaystyle \int_{S} (\nabla \times \vec{B}) \cdot d\vec{a} = \int_{S} \mu_{0} \vec{J}(\vec{r}) \cdot d\vec{a} \implies \oint_{C} \vec{B} \cdot d \vec{l} = \mu_{0}I_{inside}\)이다. 이 결과를 응용하면, 자기장의 크기가 항상 같도록 하는 앙페르 고리 C를 잡고 선적분하면, 그 결과는 앙페르 고리 면을 통과하는 전류의 양과 같다.
예를들어, 위와 같이 문제에 대칭성이 있으면 자기장을 날먹으로 구할 수 있다. 앙페르 고리 C를 다음과 같이 잡으면, \(\displaystyle \oint_{C} \vec{B} \cdot d\vec{l} = B \oint_{C} dl = B 2\pi s = \mu_{0}I \implies B = \frac{\mu_{0}I}{2\pi s}\)
[!note]- \(\nabla \cdot \vec{B} = 0\) 증명{title} \(\displaystyle \nabla \cdot \vec{B} = \frac{\mu_{0}}{4\pi} \int_{V} \nabla \cdot \left( \frac{\vec{J} \times \hat{\eta}}{\eta^2} \right) d\tau'\), \(\nabla \cdot (\vec{A} \times \vec{B})\)의 결과를 계산하면 \(\vec{B} \cdot (\nabla \times \vec{A}) - \vec{A} \cdot (\nabla \times \vec{B})\)이다. 따라서 \(\displaystyle\nabla \cdot \left( \vec{J} \times \left( \frac{\hat{\eta}}{\eta^2} \right) \right) = \frac{\hat{\eta}}{\eta^2} \cdot (\nabla \times \vec{J}) - \vec{J} \cdot \left(\nabla \times \left( \frac{\hat{\eta}}{\eta^2} \right)\right)\). \(\vec{J}(\vec{r}')\)는 \(\vec{r}'\)에 대한 함수이므로 \(\nabla\)로 미분하면 0이다. \(\displaystyle\frac{\hat{\eta}}{\eta^2}=\nabla\left( \frac{1}{\eta} \right)\)이므로 뒤의 항도 Curl Gridant이므로 0이다.
\[\therefore ~ \nabla \cdot \vec{B} = 0\]
[!note]- \(\nabla \times \vec{B} = \mu_{0} \vec{J}(\vec{r})\) 증명{title}
\[\nabla \times \vec{B} = \frac{\mu_{0}}{4\pi} \int_{V} \nabla \times \left( \frac{\vec{J}(\vec{r}') \times \hat{\eta} }{\eta^2} \right) d\tau'\]\(\nabla \times (\vec{A} \times \vec{B})\)를 \((\nabla \times (\vec{A} \times \vec{B}))_{i}\)를 통해 계산하면 \((\vec{B} \cdot \nabla) \vec{A} + \vec{A} (\nabla \cdot \vec{B}) - \vec{B}(\nabla \cdot \vec{A}) - (\vec{A} \cdot \nabla) \vec{B}\)라는 결과가 나온다. 따라서 다음과 같다.
\[\nabla \times \left( \vec{J} \times \frac{\hat{\eta}}{\eta^2} \right) = \left( \frac{\hat{\eta}}{\eta^2} \cdot \nabla \right)\vec{J} + \vec{J} \left( \nabla \cdot \frac{\hat{\eta}}{\eta^2} \right) - \frac{\hat{\eta}}{\eta^2}(\nabla \cdot \vec{J}) - (\vec{J} \cdot \nabla) \frac{\hat{\eta}}{\eta^2}\]첫째항과 셋째항은 0이다. 왜냐하면 \(\vec{J}(\vec{r}')\)는 \(\vec{r}'\)에 대한 함수인데 \(\nabla\)로 미분하고 있기 때문이다. 또, \(\displaystyle \nabla \cdot \frac{\hat{\eta}}{\eta^2} = 4\pi \delta^3(\vec{\eta})\)라는 결과를 알고 있다.
\(\displaystyle -(\vec{J} \cdot \nabla) \frac{\hat{\eta}}{\eta^2}\)는 \(\displaystyle \frac{\hat{\eta}}{\eta^2}\) 각 성분에 \(-(\vec{J} \cdot \nabla)\) 미분연산자를 적용한 것과 같다. \(\displaystyle\left( -(\vec{J} \cdot \nabla) \frac{\hat{\eta}}{\eta^2} \right)_{i} = -(\vec{J} \cdot \nabla) \left( \frac{x_{i}-x_{i}'}{\eta^3} \right) = (\vec{J} \cdot \nabla') \left( \frac{x_{i}-x_{i}'}{\eta^3} \right)\), \(\displaystyle \nabla\left( \frac{1}{\eta} \right) =- - \frac{\hat{\eta}}{\eta^2}\), \(\displaystyle \nabla'\left( \frac{1}{\eta} \right) = \frac{\hat{\eta}}{\eta^2}\)인 결과를 생각하면 \(\nabla\) 뒤에 \(\eta\)항만 미분하고 있으므로, \(\nabla'\)로 바꾸면 부호만 뒤집어주면 된다. 이걸 바꾸는 이유는, 나중에 \(\nabla' \cdot \vec{J}(\vec{r}')\) 항이 등장하기 때문이다. \(\displaystyle (\vec{J} \cdot \nabla') \left( \frac{x_{i}-x_{i}'}{\eta^3} \right)\)는 \((\vec{A} \cdot \nabla)f\) 꼴과 같은데, 이건 \(\nabla \cdot(f\vec{A}) = \vec{A} \cdot \nabla f + f(\nabla \cdot \vec{A})\) 곱셈규칙에서 등장한다. \(\vec{A} \cdot \nabla f = \nabla \cdot(f \vec{A}) - f(\nabla \cdot \vec{A})\)와 같으므로, \(\displaystyle (\vec{J} \cdot \nabla') \left( \frac{x_{i}-x_{i}'}{\eta^3} \right) = \nabla' \cdot \left( \frac{x_{i} - x_{i}'}{\eta^3} \vec{J}\right) - \left( \frac{x_{i}-x_{i}'}{\eta^3} \right)(\nabla' \cdot \vec{J}(\vec{r}'))\)이고, 뒤의 항은 Steady Current이기 때문에 0이다.
\(\displaystyle\nabla \times \vec{B} = \frac{\mu_{0}}{4\pi} \int_{V} \left( 4\pi \delta^3(\vec{\eta})\vec{J} - (\vec{J} \cdot \nabla) \frac{\hat{\eta}}{\eta^2} \right)d\tau' = \mu_{0}\vec{J} + \frac{\mu_{0}}{4\pi} \int_{V} - \left( (\vec{J} \cdot \nabla ) \frac{\hat{\eta}}{\eta^2} \right) d\tau'\)이고, 뒤 항의 적분을 성분만 살펴보면 \(\displaystyle\int_{V}\left( - (\vec{J} \cdot \nabla) \frac{\hat{\eta}}{\eta^2} \right)_{i} d\tau' = \int_{V} \nabla' \cdot\left( \frac{x_{i}-x_{i}'}{\eta^3}\vec{J} \right) d\tau' = \oint_{\partial V} \left( \frac{x_{i}-x_{i}'}{\eta^3}\vec{J} \right) \cdot d \vec{a}\)이다. V를 아주아주 크게 잡으면, 그곳의 \(\vec{J}=0\)이므로 결국 2번째 항도 0이다.
\[\therefore ~ \nabla \times \vec{B} = \mu_{0} \vec{J}(\vec{r})\]
[!tip]- \(\vec{A} \cdot \nabla\)과 \(\nabla \cdot \vec{A}\)의 차이{title} \(\nabla \cdot \vec{A}\)와 \(\vec{A} \cdot \nabla\)는 다르다. \(\displaystyle \nabla \cdot \vec{A} = \frac{{\partial A_{x}}}{\partial x} + \frac{{\partial A_{y}}}{\partial y} + \frac{{\partial A_{z}}}{\partial z}\)이고, \(\displaystyle \vec{A} \cdot \nabla = A_{x} \frac{\partial}{\partial x} + A_{y}\frac{\partial}{\partial y} + A_{z} \frac{\partial}{\partial z}\)이다. 즉 \(\nabla \cdot \vec{A}\)는 \(\vec{A}\)의 Divenserce를 계산한 것이고, \(\vec{A} \cdot \nabla\)는 그저 앞에 \(A_{i}\)항이 붙은 하나의 미분 Operator이다. 따라서 \((\vec{A} \cdot \nabla)f\)나 \((\vec{A} \cdot \nabla)\vec{B}\)와 같이 뒤에 피연산자가 붙어야 하며, 스칼라 함수의 연산 결과는 \(\displaystyle A_{x} \frac{\partial f}{\partial x} + A_{y}\frac{\partial f}{\partial y} + A_{z} \frac{\partial f}{\partial z}\)이며 벡터 함수의 연산 결과는 \(\vec{B}\)의 각각의 항을 미분한 것과 같다.
\[(\vec{A} \cdot \nabla)\vec{B} = ((\vec{A} \cdot \nabla) B_{x}, (\vec{A} \cdot \nabla)B_{y}, (\vec{A} \cdot \nabla)B_{z})\]
[!tip]- \(\displaystyle \nabla \cdot \left(\frac{\hat{\eta}}{\eta^2}\right) =\) ?{title} \(\displaystyle \nabla \cdot \left(\frac{\hat{\eta}}{\eta^2}\right) = \sum_{i} \partial_{i} \frac{(x_{i}-x_{i}')}{\eta^3} = \sum_{i}\left( \frac{1}{\eta^3} - (x_{i}-x_{i}') \partial_{i}\left( \frac{1}{\eta^3} \right) \right) = \frac{3}{\eta^3} - 3\left( \sum_{i}\frac{(x_{i}-x_{i}')^2}{\eta^5} \right)=0\)
하지만, \(\eta=0\)을 포함하는 체적 V에 대해 적분해보면 \(\displaystyle \int_{V} \nabla \cdot \left( \frac{\hat{\eta}}{\eta^2} \right)d\tau = \oint_{\partial V} \frac{\hat{\eta}}{\eta^2} \cdot d\vec{a}\), \(\vec{r}'\)를 원점으로 하고 V를 구라고 가정하면 \(\displaystyle \oint_{\partial V} \frac{\hat{r}}{r^2} \cdot \hat{r} da = \int_{\partial V} \frac{1}{r^2} r ^2\sin \theta d\theta d\phi = 4\pi\)이므로 \(\displaystyle \int_{V} \nabla \cdot \left( \frac{\hat{\eta}}{\eta^2} \right) d\tau = 4\pi\). 따라서 \(\displaystyle \nabla \cdot \left( \frac{\hat{\eta}}{\eta^2} \right) = 4\pi \delta^3(\vec{\eta})\)와 같다.
또는, 다음과 같은 방법으로 계산 가능하다.
\[\vec{E}(\vec{r})= \frac{q}{4\pi\epsilon_{0}} \frac{\hat{\eta}}{\eta^2}\] \[\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}} = \frac{q}{\epsilon_{0}} \delta^{(3)} (\vec{r} - \vec{r}')\]이므로, 두 식을 연립하면 결과를 얻을 수 있음.
[!tip]- \(\displaystyle -\nabla\left( \frac{1}{\eta} \right)=\frac{\hat{\eta}}{\eta^2}\){title} \(\displaystyle -\nabla\left( \frac{1}{r} \right)\)은 \(\displaystyle \frac{1}{r}\)에 비례하는 포텐셜을 미분한 것과 같고, 그 결과는 \(\frac{1}{r^2}\)에 비례하는 Vector Field와 같다. 이것을 생각하면 \(\displaystyle -\nabla\left( \frac{1}{\eta} \right)=\frac{\hat{\eta}}{\eta^2}\) 이 결과를 일일히 계산하지 않고 직관적으로 받아들일 수 있다.
Vector Potential
핵심
- \(\nabla \cdot \vec{B} = 0\)이므로 \(\vec{B} = \nabla \times \vec{A}\)를 만족하는 \(^\exists \vec{A}\) 존재
- \(\nabla \cdot \vec{A} = 0\)일 때, \(\nabla^2 \vec{A} = - \mu_{0} \vec{J}\)
- \(\displaystyle\vec{A}(\vec{r}) = \frac{\mu_{0}}{4\pi} \int \frac{\vec{J}(\vec{r}')}{\eta} d^3\vec{r}' = \frac{\mu_{0}}{4\pi} \int \frac{\vec{K}(\vec{r}')}{\eta} da' = \frac{\mu_{0}}{4\pi} \int \frac{\vec{I}(\vec{r}')}{\eta} dl'\)
- \(\vec{A}\)의 방향은 보통 전류의 방향과 같다.
\(\nabla \times \vec{E} =0\)이기 때문에, \(\vec{E} = - \nabla V\)를 만족하는 어떤 스칼라 필드 V가 존재했다. \(\nabla \times (- \nabla V)\)는 항상 0이기 때문이다. 똑같은 논리로, \(\nabla \cdot \vec{B} = 0\)이기 때문에, \(\vec{B} = \nabla \times \vec{A}\)를 만족하는 어떤 벡터 필드 \(\vec{A}\)가 존재한다. \(\nabla \cdot (\nabla \times \vec{A})\)가 항상 0이기 때문이다. 이때 \(\vec{A}\)를 Vector Potential이라고 한다.
Potential을 사용하여 \(\displaystyle \nabla \cdot \vec{E} = \nabla \cdot (-\nabla V) \implies \nabla^2V = - \frac{\rho}{\epsilon_{0}}\) 와 같이 Poission’s equation을 유도해냈었다. 똑같은 논리로, \(\nabla \times \vec{B} = \nabla \times (\nabla \times \vec{A}) = \nabla(\nabla \cdot \vec{A}) - \nabla^2 \vec{A} = \mu_{0}\vec{J}\)와 같다. (\(\displaystyle (\nabla \times (\nabla \times \vec{A}))_{i}=\sum_{j,k}\epsilon_{ijk}\dots\)를 사용해서 유도 가능.) 이때 \(\nabla^2 \vec{A}\)는 \(\vec{A}\)의 각 성분에 라플라시안 연산을 적용한 것과 같다.
Scalar Potential \(V\)는 상수만큼의 자유도가 존재했다. 왜냐하면 \(\vec{E} = -\nabla V\)에 \(V\)를 넣으나, \(V'+C\)를 넣으나 전기장이 같기 때문이다. Vector Potential \(\vec{A}\)는 \(\nabla f\)를 더해도 자기장이 같다. \(\vec{B} = \nabla \times \vec{A}\)에 \(\vec{A}\)를 넣으나 \(\vec{A}' + \nabla f\)를 넣으나 자기장이 같기 때문이다. \(\vec{A}\)의 이런 자유도를 Gauge Freedom이 있다고 한다. \(\vec{A}\)에 \(\nabla f\)를 더하여 Gauge Transform을 할 수 있다. 이왕이면 좋은 Gauge를 Choosing하면 문제를 쉽게 풀 수 있고, 그중 많이 사용하는 것이 \(\nabla \cdot \vec{A} = 0\)를 만족하도록 \(\vec{A}\)를 선택하는 것이다. 이를 Gauge Fixing라고 하고, \(\nabla \cdot \vec{A} = 0\) 조건을 Coulomb Gauge 라고 부른다. Coulomb Gauge를 사용하면 \(\nabla^2 \vec{A} = -\mu_{0} \vec{J}\)로 간단하게 쓸 수 있다. 자기장 버전의 포아송 방정식과 같다. 이것이 의미하는 바는, \(\nabla^2 V = - \frac{\rho}{\epsilon_{0}}\)을 푸는데 사용한 테크닉을 \(\nabla^2 A_{i} = - \mu_{0} J_{i}\)에도 적용할 수 있다는 것이다.
전기장에서 \(V(\vec{r})\)는 \(\displaystyle \frac{1}{4\pi\epsilon_{0}} \int d^3\vec{r}' \frac{\rho(\vec{r}')}{\eta}\)이다. \(\displaystyle \nabla^2 V = - \frac{\rho}{\epsilon_{0}}\) vs \(\nabla^2 \vec{A} = - \mu_{0} \vec{J}\)를 비교해보면, \(\displaystyle\frac{\rho}{\epsilon_{0}}\)를 \(\mu_{0}\vec{J}\)로만 바꿔주면 벡터 포텐셜이 된다는 것을 알 수 있다. \(\displaystyle\vec{A}(\vec{r}) = \frac{\mu_{0}}{4\pi} \int d^3\vec{r}' \frac{\vec{J}(\vec{r}')}{\eta}\) 각 성분을 따지면 \(\displaystyle A_{i}(\vec{r}) = \frac{\mu_{0}}{4\pi} \int d^3\vec{r}' \frac{J_{i}(\vec{r}')}{\eta}\)이다.
Boundry Condition
핵심
- 자기장의 수직 성분은 연속이다. \(\vec{B}_{\bot}^{above} - \vec{B}_{\bot}^{below} = 0\)
- 자기장의 평행 성분은 불연속이다. \(\vec{B}_{\parallel}^{above} - \vec{B}_{\parallel}^{below} = \mu_{0} \vec{K} \times \hat{n}\)
- 벡터 포텐셜은 항상 연속이다. \(\vec{A}_{above} = \vec{A}_{below}\)
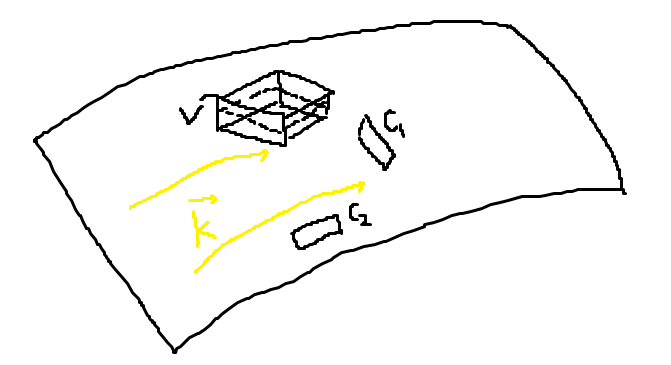
전기장과 반대로 자기장은 수직성분이 연속이고, 평행 성분이 불연속이다. 그 이유는 전기장과 자기장의 Curl, Divergence 성질이 반대이기 때문이다. 일반적인 곡면 위의 Steady Current가 \(\vec{K}\)로 주어질 때, 높이가 거의 0인 곡면을 덮는 작은 직사각형 하나를 가정하자. 부피가 V고 윗면과 아랫면의 넓이는 A라고 하자. \(\displaystyle \int_{V} \nabla \cdot \vec{B} d\tau = \oint_{\partial V} \vec{B} \cdot d \vec{a} = B_{\bot}^{above}A - B_{\bot}^{below}A = 0 \implies B_{\bot}^{above} =B_{\bot}^{below}\)이다.
\(\vec{K}\)와 수직한 앙페르 고리 \(C_{1}\)와, \(\vec{K}\)와 평행한 앙페르 고리 \(C_{2}\)를 생각해보자.
- \(\displaystyle \int_{S_{1}} \nabla \times \vec{B} \cdot d \vec{a} = \oint_{C_{1}} \vec{B} \cdot d \vec{l} = B_{\parallel}^{above}l_{\bot} - B_{\parallel}^{below}l_{\bot} = \mu_{0}I = \mu_{0}Kl_{\bot} \implies B_{\parallel}^{above} - B_{\parallel}^{below} = \mu_{0}K\)
- \(\displaystyle \int_{S_{2}} \nabla \times \vec{B} \cdot d\vec{a} = \oint_{C_{2}} \vec{B} \cdot d\vec{l} = B_{\parallel}^{above}l_{\parallel} - B_{\parallel}^{above}l_{\parallel} = \mu_{0}I_{inside} = 0 \implies B_{\parallel}^{above} - B_{\parallel}^{above} = 0\) 경계가 \(C_{2}\)인 표면을 통과하는 전류가 없기 때문에, \(\mu_{0}I_{inside} = 0\)이다.
앙페르 고리를 \(\vec{K}\)와 수직하게 설정할 때 자기장이 불연속이고, 평행하게 설정할 때 자기장이 연속이다. 이를 하나의 일반적인 식으로 표현하면 \(\vec{B}_{\parallel}^{above} - \vec{B}_{\parallel}^{below} = \mu_{0} \vec{K} \times \hat{n}\)이다. \(\hat{n}\)는 표면의 윗쪽을 가리키는 방향 벡터다.
벡터 포텐셜은 수평, 수직방향 상관없이 항상 연속이다. 그 이유는, 벡터포텐셜의 게이지를 \(\nabla \cdot \vec{A} = 0\)로 잡으면, \(\nabla \cdot \vec{B} = 0\)에 의해 수직 성분은 연속임이 보장된다. 수평 성분을 체크하기 위해 \(\nabla \times \vec{A}\)을 \(C_{1}\)이 만드는 면적으로 확인해보면, \(\displaystyle \int_{S_{1}} \nabla \times \vec{A} \cdot d \vec{a} = \int_{S_{1}} \vec{B} \cdot d \vec{a}\)인데, \(C_{1}\) 고리의 높이가 거의 0이므로 이를 통과하는 자속 또한 0이다. 따라서 평행 성분도 연속이다.
Multipole Expansion
다중극 전개를 하는 이유는, 복잡한 전하 분포를 가진 \(\rho(\vec{r}')\)가 만드는 전위를 단순화하여 해석하기 위함이다. 복잡한 전하 분포를 아주 멀리서 \((\vec{r} \gg \vec{r}')\) 본다면, 간단한 모양으로 근사하여 생각할 수 있다는 아이디어에 기반한다. 실제로 아주 복잡한 모양이더라도 멀리서 본다면 Monopole, Dipole, Quadpole, … 등과 같이 알려진 모양으로 근사된다. 미시 세계를 관측하는 우리 입장에서 아주 도움이 되는 근사법이다.
우리의 목적은 저 멀리에 있는 전기장 또는 자기장을 구하고 싶은데, 그러기 위해서 단순한 모양으로 근사된 전위 또는 벡터 포텐셜을 얻어 \(\vec{E} = -\nabla V\) 또는 \(\vec{B} = \nabla \times \vec{A}\) 식을 사용하는 것이다.
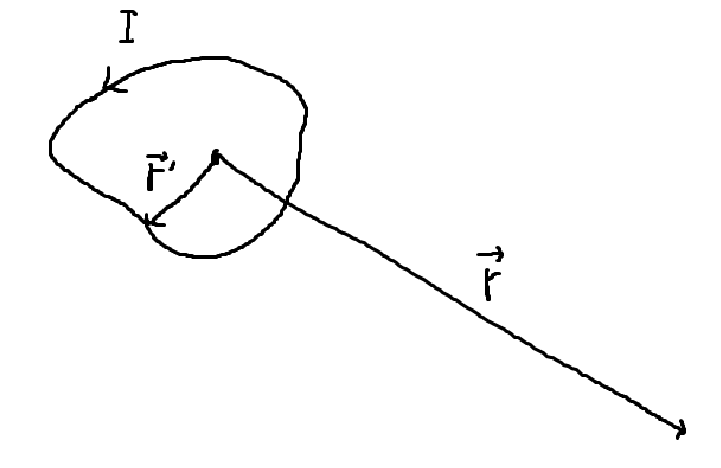
다중극 전개를 적용할 문제 상황을 위 그림과 같이 가정하자. Steady Current I가 흐르는 닫힌 도선을 멀리 바라보는 상황이다. 이때 벡터 전위는 다음과 같다.
\[\displaystyle \vec{A}(\vec{r}) = \frac{\mu_{0}}{4\pi} \oint_{C} \frac{\vec{I}}{\eta}dl' = \frac{\mu_{0}I}{4\pi} \oint_{C} \frac{d\vec{l}'}{\eta}\]- \(\eta = \lvert \vec{r} - \vec{r}' \rvert\)이다.
- \(\displaystyle \lvert \vec{r}-\vec{r}' \rvert^2 = r^2 + r'^2 - 2rr' \cos \theta = r^2\left( 1+\left( \frac{r'}{r} \right)^2-2\left( \frac{r'}{r} \right)\cos \theta \right)\)이고, \(r \gg r'\)이므로 \(\displaystyle \epsilon = \left( \frac{r'}{r} \right)^2 - 2\left( \frac{r'}{r} \right)\cos \theta\)는 아주 작은 항이다.
- \(\displaystyle \frac{1}{\eta} = \frac{1}{r} (1+\epsilon)^{-1/2}\)
- \(f(x)=(1+x)^{-1/2}\)를 테일러 전개하면 \(\displaystyle f(x)=1-\frac{1}{2}x+\frac{3}{8}x^2-\frac{5}{16}x^3+\dots\)이다.
- \(\displaystyle \frac{1}{\eta} = \frac{1}{r} (1+\epsilon)^{-1/2} \simeq \frac{1}{r^2}\left( 1-\frac{1}{2}\epsilon + \frac{3}{8}\epsilon^2 - \frac{5}{16}\epsilon^3 + \dots \right)\) \(= \frac{1}{r}\left( 1-\frac{1}{2} \left( \left( \frac{r'}{r} \right)^2 - 2\left( \frac{r'}{r} \right)\cos \theta \right) + \frac{3}{8} \left( \left( \frac{r'}{r} \right)^2 - 2\left( \frac{r'}{r} \right)\cos \theta \right) ^2 - \frac{5}{16} \left( \left( \frac{r'}{r} \right)^2 - 2\left( \frac{r'}{r} \right)\cos \theta \right)^3 + \dots \right)\)\(= \frac{1}{r} \left( 1+ \left( \frac{r'}{r} \right)\cos \theta + \left( \frac{r'}{r} \right)^2(3\cos^2\theta - 1) \frac{1}{2} + \left( \frac{r'}{r} \right)^3(5\cos^3\theta-3\cos \theta) \frac{1}{2} + \dots \right)\) \(\displaystyle = \frac{1}{r} \sum_{l=0}^\infty \left( \frac{r'}{r} \right)^l P_{l}(\cos \theta)\)
- \(\displaystyle \vec{A}(\vec{r})= \frac{\mu_{0}I}{4\pi} \oint_{C} \frac{1}{r} \sum_{l=0}^\infty \left( \frac{r'}{r} \right)^l P_{l}(\cos \theta) d\vec{l}'\). 적분에 필요 없는 \(\displaystyle\frac{1}{r}\sum_{l=0}^\infty\)을 밖으로 빼면 \(\displaystyle \vec{A}=\frac{\mu_{0}I}{4\pi}\frac{1}{r} \sum_{l=0}^\infty \oint_{C} \left( \frac{r'}{r} \right)^l P_{l}(\cos \theta) d\vec{l}'\)와 같다.
이제 위 식에서 하나씩 Sum해보면, \(\vec{A} = \displaystyle O\left( \frac{1}{r} \right) \frac{1}{r} + O\left( \frac{1}{r^2} \right) \frac{1}{r^2} + O\left( \frac{1}{r^3} \right) \frac{1}{r^3} + \dots\)와 같은 모양이 된다. 차례대로 Monopole, Dipole, Quadpole, … 항이다. \(r\)이 아주 크므로, 0이 아닌 가장 낮은 차수가 \(\vec{A}\) 급수를 주도한다. 가장 낮은 차수 외의 높은 차수는, \(r\)이 아주 크므로 무시가 가능하다.
먼저 \(l=0\)일 때 Monopole 항은 \(\displaystyle \frac{1}{r} \oint d\vec{l}'\)이다. Vector Field가 연속이고, Domain이 Simply Connected Region일 때 Vector Field의 Curl이 0이면 보존장이다. \(\nabla \times \vec{0}\) 또한 Curl이 0이므로, \(\displaystyle \oint d\vec{l}'\)는 항상 0이다. 따라서, Monopole 항은 항상 0이고, 이 결과를 통해 Magnetic Monopole 입자가 존재하지 않는다는 것을 예상할 수 있다.
\(l=1\)일 때 Diepole 항은 \(\displaystyle \frac{1}{r} \oint \left( \frac{r'}{r} \right) \cos \theta d\vec{l}' = \frac{1}{r^2} \oint r'\cos \theta d\vec{l}'\)이다. \(r'\cos \theta\)는 \(\hat{r} \cdot \vec{r}\)와도 같으므로, \(\displaystyle \oint r'\cos \theta d\vec{l}'=\oint \hat{r}\cdot \vec{r}'d\vec{l}'\). 만약 벡터 성분은 상수 벡터가 주도하고, 변수 성분은 스칼라 필드가 존재하는 \(\vec{c}f(\vec{r})\)와 같은 벡터 함수를 가정하면, \(\nabla \times \vec{c} f(\vec{r}) = - \vec{c} \times \nabla f\) 가 성립한다.
[!tip] 스칼라 함수를 닫힌 고리에 대해 적분할 때 스토크스 정리 사용하기{title}
\[\oint_{C} f(\vec{r}') d \vec{l}'\]와 같은 꼴에 스토크스 정리 \(\int_{S}(\nabla \times \vec{A}) \cdot d ave = \oint_{C} \vec{A} \cdot d \vec{l}\)를 사용하고 싶다면, \(\vec{A}(\vec{r}) = \vec{c} f(\vec{r})\)와 같이 벡터 성부는 상수가 주도하고, 변수항은 스칼라 함수가 주도하는 함수를 가정하면 된다.
\[(\nabla \times \vec{A}) \cdot d \vec{a} = (\nabla f \times \vec{c}) \cdot d\vec{a}\] \[= (d\vec{a} \times \nabla f) \cdot \vec{c} = -(\nabla \times d \vec{a} ) \cdot \vec{c}\]따라서, 다음과 같다.
\[\oint_{C} \vec{c} f \cdot d \vec{l} = \vec{c} \cdot \oint_C f d\vec{l} = - \vec{c} \cdot \int_{S} \nabla f \times d \vec{a}\] \[\implies \oint_{C} f(\vec{r}') d\vec{l'} = - \int_{S} \nabla f(\vec{r}') \times d \vec{a}'\]
\[\oint_{C} d\vec{l}' r' \cos \theta' = - \int_{S} \nabla' (\vec{r}' \cdot \hat{r}) \times d \vec{a}'\][!question]- \(\nabla \times \vec{c} f(\vec{r}) = - \vec{c} \times \nabla f\) ?{title} Consider \(\vec{w} = \vec{c} f(\vec{r})\). \(\oint \vec{W} \cdot d\vec{r} = \int_{S} \nabla \times \vec{W} \cdot d\vec{a}\)
\[\displaystyle[\nabla \times \vec{w}]_{i} = \sum_{j,k} \epsilon_{ijk} \partial_{j} w_{k} = \epsilon_{ijk} \partial_{j} c_{k} f(\vec{r}) = - \epsilon_{ikj} c_{k} \partial_{j}f(\vec{r}) = - [\vec{c} \times (\nabla f)]_{i}\] \[\therefore ~ \nabla \times \vec{c} f(\vec{r}) = - \vec{c} \times \nabla f\]
\(\nabla' (\vec{r}' \cdot \hat{r})\)가 의미하는 것은 무엇인가?
\[[\nabla' (\vec{r}' \cdot \hat{r})]_{i} = \frac{\partial}{\partial x_{i}'} \left( \sum_{j} x_{j}' (\hat{r})_{j} \right) = \sum_{j} \delta_{ij} (\hat{r})_{j} = (\hat{r})_{i}\]따라서 다음과 같다.
\[\int_{S} \nabla' (\vec{r}' \cdot \hat{r}) \times d \vec{a}' = - \hat{r} \times \int_{S} d \vec{a}' = \int_{S} d \vec{a}' \times \hat{r}\]결론적으로, \(r \gg r'\)의 상황에서 dipole vector potential은 다음과 같다.
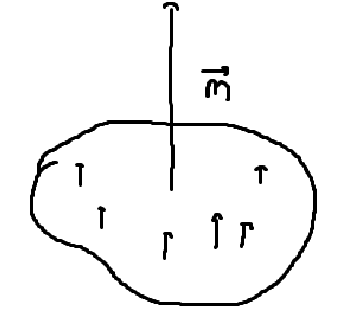
\[\therefore ~ \vec{A}_{dip}(\vec{r})= \frac{\mu_{0}I}{4\pi} \frac{1}{r^2} \left( \int_{S}d\vec{a}' \times \hat{r} \right)\]편의상 \(\displaystyle \vec{m}\equiv I \int_{S} d\vec{a}'\)라는 양을 정의하면, 다음과 같이 쓸 수 있다. 이때 \(\vec{m}\)는 Magnetic Dipole moment라고 부른다.
\[\vec{A}_{dip}(\vec{r})= \frac{\mu_{0}}{4\pi} \frac{1}{r^2} \vec{m} \times \hat{r}\]이 결과는 \(\displaystyle V_{dip}(\vec{r})= \frac{1}{4\pi\epsilon_{0}} \frac{1}{r^2} \vec{p} \cdot \hat{r}\)와 대칭적이다.
Dipole magentic field
\[\vec{B} = \nabla \times \vec{A}\]식과, Dipole vector potential을 알고 있으므로, DIpole magentic field를 계산할 수 있다. 그냥 계산하기는 어려우므로, 성분 별로 계산해보자.
\[[\vec{B}_{dip}]_{i} = [\nabla \times \vec{A}_{dip}]_{i}\] \[= \frac{\mu_{0}}{4\pi}\sum_{j,k} \epsilon_{ijk} \frac{\partial}{\partial x_{j}}\left( \frac{\vec{m} \times \vec{r}}{r^3} \right)_{k}\] \[= \frac{\mu_{0}}{4\pi}\sum_{j,k}\epsilon_{ijk} \partial_{j} \sum_{l,m}\epsilon_{klm}\left( \frac{m_{l}x_{m}}{r^3} \right)\] \[= \frac{\mu_{0}}{4\pi}\sum_{j,l,m} \left( \sum_{k}\epsilon_{ijk}\epsilon_{klm} \right)m_{l} \frac{\partial}{\partial x_{j}} \left( \frac{x_{m}}{r^3} \right)\]\(\frac{\partial}{\partial x_{j}} \left( \frac{x_{m}}{r^3} \right)\)는 \(x_{m}\)에 대해서, \(\frac{1}{r^3}\)에 대해서 곱의 미분법을 사용하면 \(\displaystyle \frac{\delta_{jm}r^3 - x_{m}3r^2 \frac{x_{j}}{r} }{r^6} = \delta_{jm} \frac{1}{r^3} - 3 \frac{x_{m}x_{j}}{r^5}\)와 같다.
\[= \frac{\mu_{0}}{4\pi} \sum_{j,l,m}m_{l}(\delta_{il}\delta_{jm} - \delta_{ik}\delta_{jl})(\delta_{jm} \frac{1}{r^3} - 3 \frac{x_{m}x_{j}}{r^5})\]\((i=l \cap j=m) ~~or ~~(i=k \cap j=l)\)를 넣고 정리하면 두 항이 상쇄되어 다음과 같이 정리할 수 있다. 한번 계산해보는 것을 권장
따라서, Dipole magnentic field \(\vec{B}_{dip}\)는 다음과 같다.
\[\vec{B}_{dip} = \frac{\mu_{0}}{4\pi}\frac{3\hat{r}(\vec{m} \cdot \hat{r}) - \vec{m}}{r^3}\]이 결과는 Dipole eletric field와 동일하다.
\[\vec{E}_{dip} = \dots\]결론적으로 Electric Dipole Field와 Magnetic Dipoel Field의 모양은 같은 모양이라는 것을 알 수 있다.
Magnetic Dipole moment
Magnetic Dipole moment인 \(\displaystyle \vec{m}= I \int_{S} d\vec{a}'\)는 무엇을 의미하는가? S는 임의의 전류 고리의 면적이다. 만약 면적이 평평하다면, 미소 법벡터 \(d\vec{a}'\)를 모두 Sum한 하나의 법선 벡터 \(\vec{m}\)가 만들어진다. 그 크기는 전류 고리의 면적과 같고, 방향은 도선에 오른손 법칙을 적용한 방향과 같다. 만약 전류 고리가 원형이면 Magnetic Dipoe moment는 \(\vec{m} = I \pi R^2 \hat{n}\)와 같다.