기초전자기학 4. 물질 속의 전기장

건국대학교 여준현 교수님의 전자기학1 수업을 정리한 내용입니다. 교재: Introduction to electrodynamics, David J. Griffths (4판)

Dipole

Dipole, 쌍극자란, 크기가 같고 반대되는 전하 또는 극이 일정 거리 떨어져 있는 상태를 뜻한다. Dipole Moment는 \((-) \to(+)\) 방향 벡터에 \(qd\)를 곱한 \(\vec{p}=q \vec{d}\)와 같다. 전자기학에서 여러 Dipole 상태가 존재하는데, 전기장 위의 중성자가 Polarized(편극)되어 하나의 쌍극자가 될 수 있고, 극성 분자 또한 하나의 쌍극자라고 볼 수 있다. 크기가 같고 부호가 반대인 두 점전하도 하나의 쌍극자로 해석할 수 있다.

하나의 쌍극자는 \(\vec{p}=q \vec{d}\)로 계산된다. 점전하가 여러개라면, 그 계의 쌍극자 모멘트의 총 합은 각 점전하의 \(q \vec{r}'\)를 합한 것과 같다. \(\displaystyle \vec{p}=\sum_{i}q_{i}\vec{r}_{i}'\). 만약 전하가 연속적으로 분포되어 있다면, 쌍극자 모멘트의 총 합은 \(\displaystyle \vec{p} = \int \vec{r}' dq\)로 계산할 수 있다. 따라서 미소 쌍극자는 \(d\vec{p}=\vec{r}' dq = \vec{r}' \rho(\vec{r}') d^3\vec{r}'\)와 같다.

Polarzation Density

Monopole가 연속된 전하 분포를 가지면 단위 부피당 들어있는 전하량인 전하 밀도를 정의하여 단위 체적당 전하 \(dq\)를 계산했다. Dipole 또한 단위 부피당 들어있는 쌍극자라는 밀도 개념을 정의하면 쌍극자를 편하게 기술할 수 있다. 이를 Polarzation density(편극 밀도)라고 하며, \(\displaystyle \vec{P}(\vec{r}') \equiv \frac{d\vec{p}}{d^3\vec{r}'}\)로 정의한다. 프라임(‘)이 붙는 이유는, Source 전하의 위치를 표기하는 양을 \(\vec{r}'\)로 정의하고 있기 때문이다. 미소 쌍극자 \(d\vec{p}=\vec{r}'\rho(\vec{r}')d^3\vec{r}'\)를 \(\vec{P}(\vec{r}')\)에 대입하면 \(\displaystyle \vec{P}(\vec{r}')=\frac{d\vec{p}}{d^3\vec{r}'}=\frac{{\vec{r}'\rho (\vec{r}') d^3\vec{r}'}}{d^3\vec{r}'} = \vec{r}' \rho(\vec{r}')\)이다. 전하 밀도와 편극 밀도는 서로 \(\vec{P}=\vec{r}' \rho\) 관계가 있음을 알 수 있다.

Dielectrics

대부분의 물질은 도체 또는 유전체 둘중 하나이다. 유전체를 DIelectrics라고 하며, 절연체라고 부르기도 한다. 현실적으로 완벽한 절연체는 없고, 아주 조금이라도 유전률을 가지고 있다. 따라서 정확히는 \(\text{Insulator} \subset \text{Dielectrics}\) 관계라고 볼 수 있다.

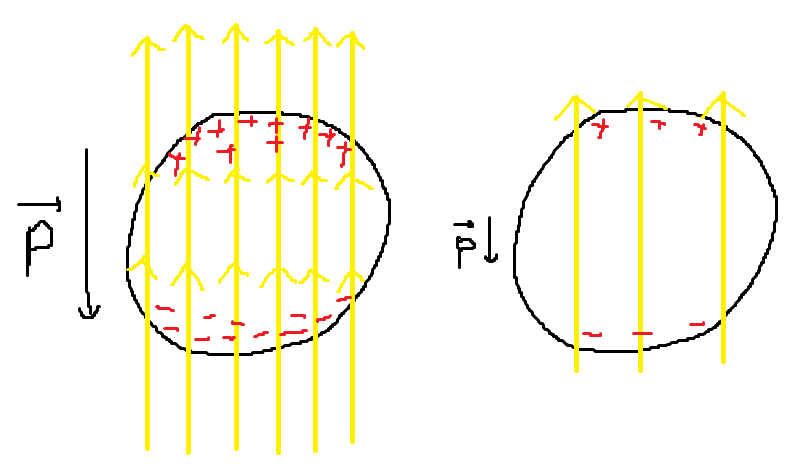
유전체는 도체와 달리 자유 전자가 돌아다니기 힘들다. 따라서 유전체의 외부에 전기장을 걸면, 원자 내부의 양성자와 전자 자체가 편극되거나, 극성 분자의 경우 분자가 회전하여 전기장 방향으로 정렬된다. 핵심은, 그 효과들이 모여 유전체의 한쪽에 +가 모이고 한쪽에 -가 모이는 효과가 생긴다는 것이다. 이런 효과를 Polarized(편극) 되었다고 하며, 편극되어 생긴 쌍극자를 유도 쌍극자 (Induiced dipole)라고 한다.

편극된 유전체가 만드는 전위는 어떻게 구할 수 있을까? 편극된 유전체의 Volume을 V라고 하자. 쌍극자 전위는 \(\displaystyle \frac{1}{r^2}\)에 비레하며, 하나의 쌍극자는 \(\displaystyle V(\vec{r})=\frac{1}{4\pi\epsilon_{0}} \frac{\hat{r}}{\hat{r}^2} \cdot \vec{p}\)로 근사할 수 있다. 전하 분포가 연속적이라면, 그 쌍극자들이 만드는 전위는 미소 쌍극자 \(d \vec{p}\)가 만드는 전위의 합과 같으므로 다음과 같다.

\[V(\vec{r}) = \frac{1}{4\pi\epsilon_{0}} \int_{V} \frac{\hat{\eta}}{\eta^2} \cdot d\vec{p} = \frac{1}{4\pi\epsilon_{0}} \int_{V}\frac{\hat{\eta}}{\eta^2} \cdot \vec{P}(\vec{r}') d^3\vec{r}'\]

\(\displaystyle \nabla' \left( \frac{1}{\eta} \right) = \frac{\hat{\eta}}{\eta^2}\)임을 이용하여 식을 고치면 \(\displaystyle \int_{V} \nabla' (\frac{1}{\eta}) \cdot \vec{P} d^3\vec{r}'\)이다. \(\nabla(f\vec{A})\) 분배법칙을 이용하면 \(\displaystyle \int_{V} \nabla' \cdot \left( \frac{1}{\eta}\vec{P} \right) d^3\vec{r}' - \int_{V} \frac{1}{\eta} \nabla' \cdot \vec{P} d^3\vec{r}'\)이다. 앞에 항을 발산 정리를 이용하여 면적분으로 쓸 수 있다.

\[\oint_{\partial V} \frac{1}{\eta} \vec{P} \cdot d\vec{a} - \int_{V} \frac{1}{\eta} \nabla' \cdot \vec{P} d^3\vec{r}'\]

각각 \(\displaystyle \frac{1}{\eta}\)에 비례하는 전위로 쓰여지는 것을 알 수 있다. Monopole의 전위가 \(\displaystyle \frac{1}{\eta}\)에 비레하고, 마치 \(\displaystyle \int \frac{1}{\eta} \rho d^3\vec{r}'\) 꼴과 비슷하다고 느껴진다. \(\displaystyle \sigma_{b} \equiv \vec{P} \cdot \hat{n}\), \(\rho_{b}\equiv-\nabla' \cdot \vec{P}\)로 정의하면 유도된 쌍극자가 만드는 전위는 표면의 Bound Charge(속박전하)가 만드는 전위 + 표면 내의 Bound Charge가 만드는 전위의 합으로 계산할 수 있다.

\[\displaystyle V(\vec{r})= \frac{1}{4\pi\epsilon_{0}} \oint_{\partial V} \frac{1}{\eta} \sigma_{b}(\vec{r}') da + \frac{1}{4\pi\epsilon_{0}} \int_{V} \frac{1}{\eta} \rho_{b}(\vec{r}') d^3\vec{r}'\]

Electric Displacement

대체 전기장은, \(\vec{D}=\epsilon_{0}\vec{E} + \vec{P}\)이고 \(\nabla \cdot \vec{D} = \rho_{fre e}\)를 만족하는 식이다. 양 변을 체적적분하여 적분꼴로 바꾸면 \(\displaystyle \oint_{S} \vec{D} \cdot d \vec{a} = Q_{fre e, ~in}\)이다. 문제에 대칭성이 있고, Material에 삽입한 자유 전자를 알고 있는 특별한 조건일 경우 대체전기장으로 전기장을 구할 수 있다. 대칭성이 있다면 가우스 법칙으로 \(\vec{D}\)를 구할 수 있고, \(\vec{P}\)를 안다면 바로 전기장 \(\vec{E}\)를 알 수 있다. 유전체 외부의 \(\vec{P}\)는 0이므로 보통 외부의 전기장은 \(\displaystyle \vec{E} = \frac{1}{\epsilon_{0}}\vec{D}\)으로 구할 수 있다. 유전체 내부는 \(\vec{P}\)를 모른다면 다른 방법으로 구해야 한다.

유전체 전체의 \(\rho\)는 편극되어 생기는 \(\rho_{b}\) 뿐만 아니라 외부에서 들어온 자유전자 \(\rho_{f}\)가 존재할 수 있다. 가우스 법칙을 \(\displaystyle \nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}} \implies \epsilon_{0}\nabla \cdot \vec{E} = {\rho_{b} + \rho_{f}} = -\nabla \cdot \vec{P} + \rho_{f} \implies \nabla \cdot (\epsilon_{0}\vec{E} + \vec{P}) = \rho_{f}\) 여기서 \(\vec{D}\equiv \epsilon_{0} \vec{E} + \vec{P}\)로 정의한다. \(\vec{D}\)는 전기장과는 다르다. 쿨롱 법칙으로 \(\vec{D}\)를 구할 수도 없으며, \(\nabla \times \vec{D} \neq 0\) Curl도 0이 아니다.

Linear Dielectrics

유전체의 외부에 걸린 전기장의 세기가 셀수록 편극되는 정도가 강하고, 전기장의 세기가 약할수록 편극되는 정도가 약할것이라는 짐작은 간다. 이 편극되는 정도가 전기장에 비례하는 유전체를 Linear Dielectrics라고 한다. Linear Dielectrics는 \(\vec{P} \propto \vec{E}\) 관계에 있다. 비례상수를 편의상 \(\epsilon_{0}X_{e}\)로 정의하면, \(\vec{P}=\epsilon_{0}X_{e}\vec{E}\)로 쓸 수 있다. 이때 \(X_{e}\)는 매질의 감수율(electric susceptibility)이라고 한다. 감수율은 Material이 편극이 얼마냐 잘되냐를 나타내는 무차원 상수값이다.

\(\vec{P}= \epsilon_{0} X_{e}\vec{E}\) 를 사용해 \(\vec{D}\)을 다시 표현하면 \(\vec{D}=\epsilon_{0}\vec{E} + \epsilon_{0}X_{e}\vec{E} = \epsilon_{0}(1+X_{e})\vec{E}\)이다. \(e_{r}\equiv1+X_{e}\)라고 정의한다. 이를 유전 상수(dielectric constant) 또는 상대 유전율이라고 부른다. 유전 상수값은 1보다 크며, 이 값이 클수록 편극이 잘 일어남을 의미한다. 진공의 유전 상수를 \(\epsilon_{0}\)으로 기준잡고, \(\epsilon_{0}=1\)이다. 유전 상수는 무차원 수이므로, 최종적으로 \(\epsilon \equiv \epsilon_{0}\epsilon_{r}\)로 정의하며, 이를 재로의 유전율(permittivity)라고 한다. 단위는 \(F / m\)이다. 실제 \(\epsilon_{0}\)는 대략 \(8.8541878×10^{−12}F⋅m^{−1}\) 정도이다.

유전율과 유전 상수의 차이는, 유전율은 차원을 갖고있는 실제 물리량이고, 유전 상수는 편의상 \(\epsilon_{0}=1\)로 기준잡은 상대 유전율이라고 보면 된다. 유전 상수는 그저 물질 간의 편극이 얼마나 잘일어나는지 사람이 보기 편하게 정의한 값이고, 실제 물리적인 계산은 유전율을 사용해야 한다.

\[\rho_{b}= - \nabla \cdot \vec{P} = - \epsilon_{0}X_{e} \nabla \cdot \vec{E} = - \epsilon_{0} X_{e} \frac{\rho}{\epsilon_{0}} = -X_{e}(\rho_{b}+\rho_{f})\] \[\implies (1+X_{e})\rho_{b} = -X_{e}\rho_{f} \implies \rho_{b} = - \frac{X_{e}}{1+X_{e}}\rho_{f}\]

관계를 얻어낸다. 따라서 선형 유전체일 경우에는, 표면이 아닌 부분의 전하 분포 \(\rho_{b}\)는 편극으로 생기지 않는다.

우리가 알 수 있는 정보가 두가지가 있다. 첫번째는, 유전체를 Linear Dielectrics로 가정하면 \(\vec{P}\)를 \(\epsilon_{0}X_{e}\vec{E}\)로 사용하여 문제 상황에서 대칭성이 있는 경우 대체 전기장 \(\displaystyle \vec{E}=\frac{1}{\epsilon}\vec{D}\)을 사용하여 편하게 전기장을 구할 수 있다. 두번째는, 선형 유전체의 경우 물질 내부의 Bound Charge(\(\rho_{b}\))는 자연적으로 생기지 않는다. 표면의 \(\sigma_{b}\)만 존재한다.

[!example]- 외부에 균일한 전기장 \(\vec{E}=E_{0}\hat{z}\) 속에 선형 유전체로 된 공이 있을 때, 공 내부의 전기장을 구하라.{title} 선형 유전체는 자연적으로 \(\rho_{b}\)가 생기지 않으므로, \(\sigma_{b}\)만 존재하고 아래쪽에 -, 위쪽에 +로 편극되었을 것이다. 이 편극된 전하는 전기장을 상쇄하는 방향으로 전기장을 만들지만, 완전히 다 상쇄시키지는 못하고 일부만 상쇄시킨다.