기초전자기학 24. 도체 속 전자기파는 어떻게 거동할까

도체 속 전자기파는 어떻게 거동할까?

이번엔 자유 전하밀도와 자유 전류가 0이 아닌 경우를 살펴보자.

\[\rho_{f} \neq 0, ~~\vec{J}_{f} \neq 0\]

자유 전하밀도가 있다는 것은, 자유롭게 돌아다닐 수 있는 전하가 존재한다는 뜻이고, 이는 매질이 도체임을 의미한다. 일반적으로 도체는 옴 법칙을 만족하며, 옴 법칙에 따라 도체 속의 자유 전류밀도는 전기장과 비례함을 알 수 있다.

\[\vec{J}_{f} = \sigma \vec{E}\]

• 도체에서 선형 매질이란, 옴 법칙을 만족하는 도체와 같다.`
• 유전체에서 선형 매질이란, \(\vec{P} = \epsilon_{0}X_{e}\vec{E}\)을 만족하는 유전체와 같다.
• 자성체에서 선형 매질이란, \(\vec{M} = X_{m}\vec{H}\) 을 만족하는 자성체와 같다.

이때 맥스웰 방정식은 다음과 같다.

\[\nabla \cdot \vec{E} = \frac{\rho_{f}}{\epsilon}, ~~\nabla \cdot \vec{B} = 0, ~~\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}, ~~\nabla \times \vec{B} = \mu \sigma \vec{E} + \mu\epsilon \frac{\partial \vec{E}}{\partial t}\]

[!question] 도체에서 \(\vec{D}, \vec{H}\)를 사용하지 않는 이유가 무엇인가?{title}

\[\vec{D} = \epsilon_{0}\vec{E} + \vec{P}, ~~\vec{H} = \frac{1}{\mu_{0}}\vec{B} - \vec{M}\]

이때 편극 밀도, 자화 밀도는 유전체, 자성체에서 얼마나 편극되는지 나타내는 지표와 같다. 도체에선 자유 전자가 존재할 수 있기 때문에 편극의 효과가 미미하다. 따라서 \(\vec{D}, \vec{H}\)를 사용하지 않는다.

자유 전류와 자유 전하 밀도는 연속방정식을 만족한다.

\[\nabla \cdot \vec{J}_{f} = - \frac{\partial \rho_{f}}{\partial t}\]

옴 법칙과, 가우스 법칙을 적용하면 다음과 같다.

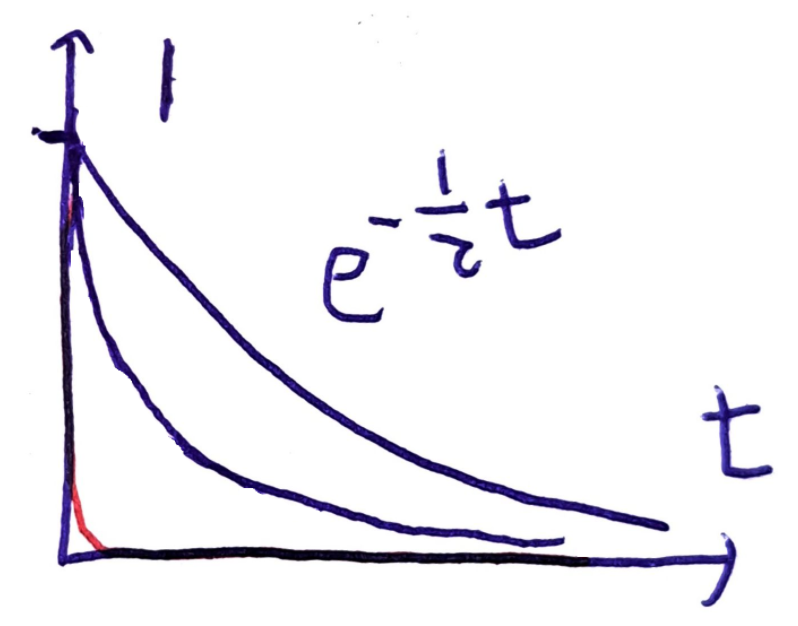
\[\nabla \cdot (\sigma \vec{E}) = - \frac{\partial \rho_{f}}{\partial t}\] \[\implies \sigma \nabla \cdot \vec{E} = - \frac{\partial \rho_{f}}{\partial t}\] \[\implies -\frac{\sigma }{\epsilon}\rho_{f} = \frac{\partial\rho_{f}}{\partial t}\] \[\implies \rho_{f}(t) = \rho_{f}(0)e^{- (\sigma / \epsilon)t}\]

시간 \(t=0\)일 때 초기 자유전하 \(\rho_{f}(0)\)만큼이 존재하고, 시간이 지날 수록 \(\rho_{f} \to 0\)으로 다가간다. \(\rho\)는 단위 부피당 전하를 뜻한다. \(\rho_{f}\to 0\)으로 다가간다는 의미는, 도체 속의 자유 전하가 모두 흩어져 표면으로 이동함을 뜻한다. 따라서 표면 전하밀도 \(\sigma_{f}\)는 0이 아니다. 이는 도체 내부의 전기장이 0이 될때까지 전하가 재배열된다는 사실을 다시 보여준다.

\(\tau \equiv \frac{\epsilon}{\sigma}\)라고 하자. \(\tau\)가 작을 수록 자유 전하가 더 빨리 흩어진다. 만약 아주 좋은 도체, \(\sigma \to \infty\)인 경우 \(\tau \to 0\)이므로, \(e^{-(1/\tau) t}\)는 0이다.

자유 전하가 모두 흩어진 경우 \(\rho_{f}=0\)이며, 이때의 맥스웰 방정식은 다음과 같다.

\[\nabla \cdot \vec{E} = 0, ~~\nabla \cdot \vec{B} = 0, ~~\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}, ~~\nabla \times \vec{B} = \mu \sigma \vec{E} + \mu \epsilon \frac{\partial \vec{E}}{\partial t}\]

3, 4번 식에 Curl을 취하면 다음 결과를 얻는다.

[!NOTE]- 유도 과정{title}

\[\nabla \times (\nabla \times \vec{E}) = \nabla \times \left( -\frac{\partial \vec{B}}{\partial t} \right)\]

이때, 벡터의 삼중곱으로 \(\nabla \times (\nabla \times \vec{A}) = \nabla(\nabla \cdot \vec{A}) - \nabla^2 \vec{A}\)와 같다. 따라서 다음과 같다.

[!question] 벡터의 삼중곱 적용하면 \(\nabla \times (\nabla \times \vec{A}) = \nabla (\nabla \cdot \vec{A}) - \vec{A} (\nabla \cdot \nabla)\) 이거 아닌가?{title} 좌변의 연산 결과는 벡터가 나와야 한다. 그러나 우변의 연산 결과는 벡터 - 연산자 형태다. 벡터의 삼중 곱 꼴은 무엇인가?

\[\vec{A} \times (\vec{B} \times \vec{C}) = \vec{B}(\vec{A} \cdot \vec{C}) - \vec{C}(\vec{A} \cdot \vec{B})\]

우변은 (벡터 \(\cdot\) 스칼라) 꼴이므로, 이를 (스칼라 \(\cdot\) 벡터) 꼴로 바꿔도 무방하다.

\[\vec{A} \times (\vec{B} \times \vec{C}) = \vec{B}(\vec{A} \cdot \vec{C}) - (\vec{A} \cdot \vec{B})\vec{C}\]

위 식을 적용하면, 우리가 원하는 결과를 얻을 수 있다.

\[\nabla \times (\nabla \times \vec{A}) = \nabla (\nabla \cdot \vec{A}) - (\nabla \cdot \nabla) \vec{A} = \nabla(\nabla \cdot \vec{A}) - \nabla^2\vec{A}\]

\[\nabla(\nabla \cdot \vec{E}) - \nabla^2 \vec{E} = -\frac{\partial}{\partial t}(\nabla \times \vec{B})\] \[\implies - \nabla^2 \vec{E} = - \frac{\partial}{\partial t}\left( \mu \sigma \vec{E} + \mu\epsilon \frac{\partial \vec{E}}{\partial t} \right)\] \[\therefore ~~ \nabla^2\vec{E} = \mu \sigma \frac{\partial \vec{E}}{\partial t} + \mu\epsilon \frac{\partial^2\vec{E}}{\partial t^2}\]

4번 식에 Curl을 취해보자.

\[\nabla \times (\nabla \times \vec{B}) = \nabla \times \left( \mu \sigma \vec{E} + \mu\epsilon \frac{\partial \vec{E}}{\partial t} \right)\] \[\implies \nabla(\nabla \cdot \vec{B}) - \nabla^2\vec{B} = \mu \sigma \nabla \times \vec{E} +\mu\epsilon \frac{ \partial}{\partial t} (\nabla \times \vec{E})\] \[\implies - \nabla^2\vec{B} = \mu \sigma \left( -\frac{\partial \vec{B}}{\partial t} \right) + \mu\epsilon\frac{ \partial}{\partial t}\left( -\frac{\partial \vec{B}}{\partial t} \right)\] \[\therefore ~~ \nabla^2 \vec{B} = \mu \sigma \frac{\partial \vec{B}}{\partial t} + \mu\epsilon \frac{\partial^2 \vec{B}}{\partial t^2}\]

\[\therefore ~~ \nabla^2\vec{E} = \mu \sigma \frac{\partial \vec{E}}{\partial t} + \mu\epsilon \frac{\partial^2\vec{E}}{\partial t^2}\] \[\therefore ~~ \nabla^2 \vec{B} = \mu \sigma \frac{\partial \vec{B}}{\partial t} + \mu\epsilon \frac{\partial^2 \vec{B}}{\partial t^2}\]

파동 방정식에서 시간에 대해 한번 미분된 항이 추가됐다. 우리가 기존에 알던 Solution을 Try 해보자.

\[\tilde{\vec{E}}(z, t) = \tilde{\vec{E}}_{0}e^{i(kz - \omega t)}, ~~\tilde{\vec{B}}(z, t) = \tilde{\vec{B}}_{0}e^{i(kz - \omega t)}\]

이 Solution을 미분 방정식에 넣어보면, 다음 관계가 성립해야 한다.

\[(ik)^2 = \mu \sigma (-i\omega) + \mu\epsilon (-i\omega)^2\] \[\implies -k^2 = - i\mu \sigma \omega -\mu\epsilon \omega^2\] \[\implies k^2 = i \mu\sigma \omega + \mu\epsilon \omega^2\]

즉, \(k\)가 복소수이기만 하면 문제는 해결된다!

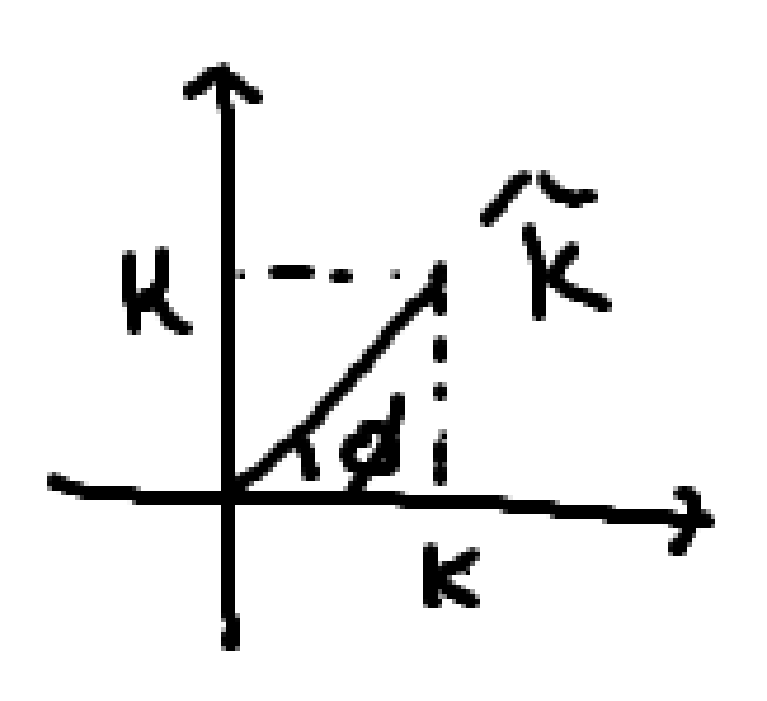
\[\tilde{k}^2 = i \mu \sigma \omega + \mu \epsilon \omega^2\]

그럼, \(\tilde{k}\)는 무엇일까? \(\tilde{k} = k + i\kappa\)라고 두고, \(\tilde{k}\)를 구했을때 결과는 다음과 같다.

[!NOTE]- 유도 과정{title}

\[(k+i\kappa)^2 = i\mu \sigma \omega + \mu\epsilon \omega^2\] \[\implies k^2 + i 2k\kappa - \kappa^2 = i \mu \sigma \omega + \mu\epsilon \omega^2\]

Real 파트를 살펴보자.

\[k^2 - \kappa^2 = \mu\epsilon \omega^2\]

Image 파트를 살펴보자.

\[2k \kappa = \mu \sigma \omega \implies \kappa = \frac{\mu \sigma \omega}{2k}\]

이를 Real 파트에서 구한 식에 대입한다.

\[k^2 - \frac{(\mu \sigma \omega)^2}{4k^2} = \mu\epsilon \omega^2\] \[\implies 4k^4 - 4\mu\epsilon \omega^2 k^2 - (\mu \sigma \omega)^2 = 0\]

이는, \(k^2\)에 대한 2차방정식이다. 해는 다음과 같다.

\[k^2 = \frac{-(b / 2) \pm \sqrt{ (b / 2)^2-ac }}{a} = \frac{2\mu\epsilon \omega^2 \pm \sqrt{ (2\mu\epsilon \omega^2)^2 - (-4(\mu \sigma \omega)^2) }}{4}\] \[= \frac{2\mu\epsilon \omega^2 \pm \sqrt{ (2\mu\epsilon \omega^2)^2 + (2\mu \sigma \omega)^2}}{4}\]

항상 \(2\mu\epsilon \omega^2 < \sqrt{ (2\mu\epsilon \omega^2)^2 + (\mu \sigma \omega)^2 }\)이므로, 음수는 제외한다. \(k\)는 실수이기 때문이다.

\[k^2 = \frac{2\mu\epsilon \omega^2 + \sqrt{ (2\mu\epsilon \omega^2)^2 + (2\mu \sigma \omega)^2 }}{4} = \frac{1}{2}\mu\epsilon \omega^2 + \frac{1}{2} \mu\epsilon \omega^2\sqrt{ 1 + \frac{(\mu \sigma \omega)^2}{(\mu\epsilon \omega^2)^2} }\] \[= \frac{1}{2} \mu\epsilon \omega^2\left[ 1 + \sqrt{ 1+ \left( \frac{\sigma}{\epsilon \omega} \right)^2 } \right]\]

따라서, \(\kappa\)는 다음과 같다.

\[\frac{1}{2}\mu\epsilon \omega^2\left[ 1+ \sqrt{ 1+\left( \frac{\sigma}{\epsilon \omega} \right)^2 } \right] - \kappa^2 = \mu\epsilon \omega^2\] \[\implies \kappa^2 = \frac{1}{2}\mu\epsilon \omega^2\left[ 1+\sqrt{ 1+\left( \frac{\sigma}{\epsilon \omega} \right)^2 } \right] - \mu\epsilon \omega^2\] \[= \frac{1}{2}\mu\epsilon \omega^2\left[ 1 + \sqrt{ 1+\left( \frac{\sigma}{\epsilon \omega} \right)^2 } - 2 \right] = \frac{1}{2}\mu\epsilon \omega^2\left[ -1 + \sqrt{ 1+ \left( \frac{\sigma}{\epsilon \omega} \right)^2 } \right]\]

\[\therefore ~~ k = \omega \sqrt{ \frac{\mu\epsilon}{2} } \left[ 1 + \sqrt{ 1 + \left( \frac{\sigma}{\epsilon \omega} \right)^2 } \right]^{1/2}\] \[\therefore ~~ \kappa = \omega \sqrt{ \frac{\mu\epsilon}{2} } \left[ \sqrt{ 1 + \left( \frac{\sigma}{\epsilon \omega} \right)^2 } - 1 \right]^2\]

[!question] 위 결과가 정확한가?{title} 만약 도체가 아니라 \(\sigma \to 0\)이면, \(k = \frac{\omega}{v} \sqrt{ \frac{1}{2} } \sqrt{ 2 } = \frac{\omega}{v}\), \(\omega = kv\) 기존의 사실과 모순되지 않는다. 또, \(\kappa = \omega \sqrt{ \frac{\mu\epsilon}{2} } (1-1) = 0\)이므로, 허수부가 없던 기존의 사실과 모순되지 않는다.

그렇다면, \(\tilde{k}\)가 허수라는 뜻은, 물리적으로 무슨 의미를 가질까?

\[\tilde{\vec{E}}(z,t) = \tilde{\vec{E}}_{0} e^{i((k + i \kappa) z - \omega t)} = \tilde{\vec{E}}_{0}e^{-\kappa z} e^{i(kz - \omega t)}\] \[\tilde{\vec{B}}(z,t) = \tilde{\vec{B}}_{0} e^{i((k + i \kappa) z - \omega t)} = \tilde{\vec{B}}_{0}e^{-\kappa z} e^{i(kz - \omega t)}\]

전자기파 진폭에 감쇠계수 \(e^{-\kappa z}\)가 붙는다. \(+z\)가 진행 방향이므로, 즉 도체 내부로 진행할 수록 전자기파가 감소한다. 이때, 침투 깊이(skin depth) 를 다음과 같이 정의한다.

\[\lambda \equiv \frac{1}{\kappa}\]

이는 진폭이 \(\frac{1}{e} \simeq \frac{1}{3}\)만큼 줄어드는 거리를 의미하며, 도체 내부로 전자기파가 얼마나 침투할 수 있는지에 대한 지표로 사용된다.

좋은 도체 \(\sigma\to \infty\)이면 \(\kappa \to \infty\)이므로 \(\lambda \to 0\)이다. 즉, 좋은 도체일 수록 전자기파가 침투하기 어렵다. 반대로, \(\sigma \to 0\)이면 \(\kappa \to 0\)이므로 \(\lambda \to \infty\)이다. 즉, 유전체면 전자기파가 침투할 수 있다.

Solution의 모양이 전자기 파동 방정식의 해와 \(\tilde{k}\)만 차이나므로, 맥스웰 방정식에 의해 다음 결과를 똑같이 얻는다.

\[\nabla \cdot \vec{E} \to E_{z,0} = 0\] \[\nabla \cdot \vec{B} \to B_{z, 0} = 0\] \[\nabla \times \vec{E} \to \tilde{\vec{B}}_{0} = \frac{\tilde{k}}{\omega}(\hat{z} \times \tilde{\vec{E}}_{0})\]

\(\nabla \times \vec{B}\)는 위와 같은 결과를 얻는다.

[!example] example{title} 전기장과 자기장의 방향을 다음과 같이 설정해보자.

\[\tilde{\vec{E}}_{0} = \hat{x} E_{0} e^{i \delta_{E}}, ~~\tilde{\vec{B}}_{0} = \frac{\tilde{k}}{\omega} (\hat{z} \times \hat{x} E_{0}e^{i \delta_{E}}) = \hat{y} \frac{\tilde{k}}{\omega} E_{0}e^{i \delta_{E}}\]

\(\tilde{k}\)를 다음과 같이 설정할 수 있다.

\[\tilde{k} = \lvert \tilde{k} \rvert e^{i \phi}\]

따라서, 실수 전기장과 자기장은 다음과 같다.

\[\vec{E}(z,t) = E_{0} e^{-\kappa z}\cos(kz - \omega t + \delta_{E})\] \[\vec{B}(z,t) = \frac{\lvert \tilde{k} \rvert}{\omega} E_{0} e^{-\kappa z} \cos(kz - \omega t + \delta_{E} + \phi)\]

전기장과 자기장의 위상이 \(\phi\)만큼 차이남을 알 수 있다.

이때, \(\lvert \tilde{k} \rvert\)은 다음과 같다.

\[\lvert \tilde{k} \rvert = \sqrt{ k^2 + \kappa^2 } = \sqrt{ \frac{1}{2} \mu\epsilon \omega^2\left[ 1 + \sqrt{ 1+ \left( \frac{\sigma}{\epsilon \omega} \right)^2 } \right] + \frac{1}{2} \mu\epsilon \omega^2\left[ -1 + \sqrt{ 1+ \left( \frac{\sigma}{\epsilon \omega} \right)^2 } \right] }\] \[= \sqrt{ \mu\epsilon \omega^2 \sqrt{ 1+ \left( \frac{\sigma}{\epsilon \omega} \right)^2} }\]

\(\phi\)는 복소평면을 생각해보면 쉽게 구할 수 있다.

\[\tan \phi = \frac{\kappa}{k} \implies \phi = \tan^{-1}\left( \frac{\kappa}{k} \right)\]