기초전자기학 23. 유전체 속 전자기파는 어떻게 거동할까

유전체 속 전자기파는 어떻게 거동할까?

자유 전하가 없다는 것은, 자유롭게 돌아다닐 수 있는 전하가 없다는 것과 같고, 이는 이상적인 유전체와 같다.

맥스웰 방정식을 연립해서, 파동 방정식을 만들고, 그 파동 방정식의 파동을 단색 평면파 조건을 사용하여 얻은 전기장과 자기장의 해는 다음과 같다.

\[\tilde{\vec{E}}(\vec{r},t) = \tilde{\vec{E}}_{0}e^{i(\vec{k} \cdot \vec{r} - \omega t)}\] \[\tilde{\vec{B}}(\vec{r},t) = \tilde{\vec{B}_{0}}e^{i(\vec{k} \cdot \vec{r} - \omega t)}\]

즉, 이는 단색 평면파의 일반적인 Solution이다.

진공에서의 맥스웰 방정식은 다음과 같고, 이 맥스웰 방정식에서 바운더리 컨디션을 통해 얻어낸 정보는 다음과 같았다.

\[\nabla \cdot \vec{E} = 0, ~~\nabla \cdot \vec{B} = 0, ~~\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}, ~~\nabla \times \vec{B} = \mu_{0}\epsilon_{0} \frac{\partial \vec{E}}{\partial t}\] \[\tilde{E}_{z} = \tilde{B}_{z} = 0\] \[\tilde{\vec{B}}_{0} = \frac{1}{c} \hat{k} \times \tilde{\vec{E}}_{0}\]

매질에서 자유 전하, 자유 전류가 없는 상황 속 맥스웰 방정식은 다음과 같다.

\[\nabla \cdot \vec{D} = 0, ~~ \nabla \cdot \vec{B} = 0, ~~\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}, ~~\nabla \times \vec{H} = \frac{\partial \vec{D}}{\partial t}\]

우리는 선형 유전체를 고려한다. \(\vec{D}, \vec{H}\)과 \(\vec{E}, \vec{B}\)의 관계는 다음과 같다.

\[\vec{D} = \epsilon \vec{E}, ~~\vec{H} = \frac{1}{\mu}\vec{B}\]

이를 맥스웰 방정식에 대입하면 다음과 같다.

\[\nabla \cdot (\epsilon \vec{E}) = 0, ~~\nabla \cdot \vec{B} = 0, ~~\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}, ~~\nabla \times \left( \frac{1}{\mu}\vec{B} \right) = \frac{\partial(\epsilon \vec{E})}{\partial t}\] \[\implies \nabla \cdot \vec{E} = 0, ~~ \dots, ~~\nabla \times \vec{B} = \epsilon\mu \frac{\partial \vec{E}}{\partial t}\]

이는 진공 속 맥스웰 방정식에서 \(\epsilon_{0}\mu_{0}\)가 단순히 \(\epsilon \mu\)로 바뀐 것과 같다. 따라서, 진공 속 단색 평면파의 수식에서 상수만 치환하면 자유 전하가 없는 매질 속 단색 평면파로 생각할 수 있다.

\[\tilde{E}_{z}= \tilde{B}_{z} = 0\] \[\tilde{\vec{B}}_{0} = \frac{1}{c} \hat{k} \times \tilde{\vec{E}}_{0}\]

이때 전자기파의 속도는 다음과 같다.

\[v=\frac{1}{\sqrt{ \epsilon \mu }}\]

진공에서의 속도는 다음과 같다.

\[c= \frac{1}{\sqrt{ \epsilon_{0}\mu_{0} }}\]

다음 상수를 도입한다.

\[n \equiv \sqrt{ \frac{\epsilon \mu}{\epsilon_{0}\mu_{0}} }\]

이를 물질의 굴절율(index of refraction) 이라고 한다. 매질 속 전자기파의 속도를 굴절율로 다음과 같이 쓸 수 있다.

\[n = \sqrt{ \frac{\epsilon \mu}{\epsilon_{0} \mu_{0}} } = \frac{c}{v} \implies v= \frac{c}{n}\]

대부분의 물질은 \(\mu\)값이 \(\mu_{0}\)와 가깝다. 따라서, 굴절율은 다음과 같다.

\[n \simeq \sqrt{ \frac{\epsilon}{\epsilon_{0}} } = \sqrt{ \epsilon_{\text{상대}} }\]

\(\epsilon_{\text{상대}}\)는 항상 1보다 크므로, 속도 \(v\)는 항상 \(c\)보다 작다. 이는 직관적으로 당연한 사실이다.

에너지 밀도, 포인팅 벡터, 전자기파의 세기는 각각 다음과 같다.

\[u=\frac{\epsilon}{2}E^2 + \frac{1}{2\mu}B^2\] \[\vec{S} = \frac{1}{\mu}(\vec{E} \times \vec{B})\] \[I = \frac{1}{2}\epsilon v E_{0}^2\]

결론적으로, 유전체 속 전자기파는 진공 속 전자기파에서 상수값만 바꾸면 동일한 결과를 얻는다.

\[\epsilon_{0}\mu_{0} \to \epsilon \mu\]

두 유전체 경계에 단색 평면파를 수직으로 입사시키면?

물질 속의 Boundry Condition은 다음 맥스웰 방정식에서 유도된다. 이때 자유 전하, 자유 전류가 없는 상황을 고려한다.

\[\nabla \cdot \vec{D} = 0, ~~ \nabla \cdot \vec{B} = 0, ~~\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}, ~~\nabla \times \vec{H} = \frac{\partial \vec{D}}{\partial t}\] \[D_{1}^{\bot} = D_{2}^{\bot}, ~~ B_{1}^{\bot} = B_{2}^{\bot}, ~~\vec{E}^{\parallel}_{1} = \vec{E}^{\parallel}_{2}, ~~\vec{H}^{\parallel}_{1} = \vec{H}^{\parallel}_{2}\] \[\implies \epsilon_{1}E_{1}^{\bot} = \epsilon_{2}E_{2}^{\bot}, ~~B_{1}^{\bot} = B_{2}^{\bot}, ~~\vec{E}_{1}^{\parallel} = \vec{E}_{2}^{\parallel}, ~~\mu_{1}\vec{B}^{\parallel}_{1} = \mu_{2}\vec{B}^{\parallel}_{2}\]

[!note] 왜 \(\vec{E}^{\parallel}_{1} = \vec{E}^{\parallel}_{2}, ~~\vec{H}^{\parallel}_{1} = \vec{H}^{\parallel}_{2}\)인가?{title}

\[\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}\implies \int \nabla \times \vec{E} \cdot d\vec{a} = - \frac{\partial}{\partial t} \int \vec{B} \cdot d \vec{a}\]

이때, 면적을 매우 작게 설정하므로 그 면적을 통과하는 자기 선속은 0과 같다.

\[\implies \oint \vec{E} \cdot d\vec{l} = 0\implies \vec{E}^{\parallel}_{1} = \vec{E}^{\parallel}_{2}\] \[\nabla \times \vec{H} = \frac{\partial \vec{D}}{\partial t}\implies\int \nabla \times \vec{H} \cdot d\vec{a} = \frac{\partial}{\partial t} \int \vec{D} \cdot d\vec{a}\]

\(\vec{D} = \epsilon \vec{E}\)이다. 같은 논리로, 좁은 면적을 통과하는 전기장의 선속은 0과 같다.

\[\implies \oint \vec{H} \cdot d\vec{l} = 0\implies \vec{H}^{\parallel}_{1} = \vec{H}^{\parallel}_{2}\]

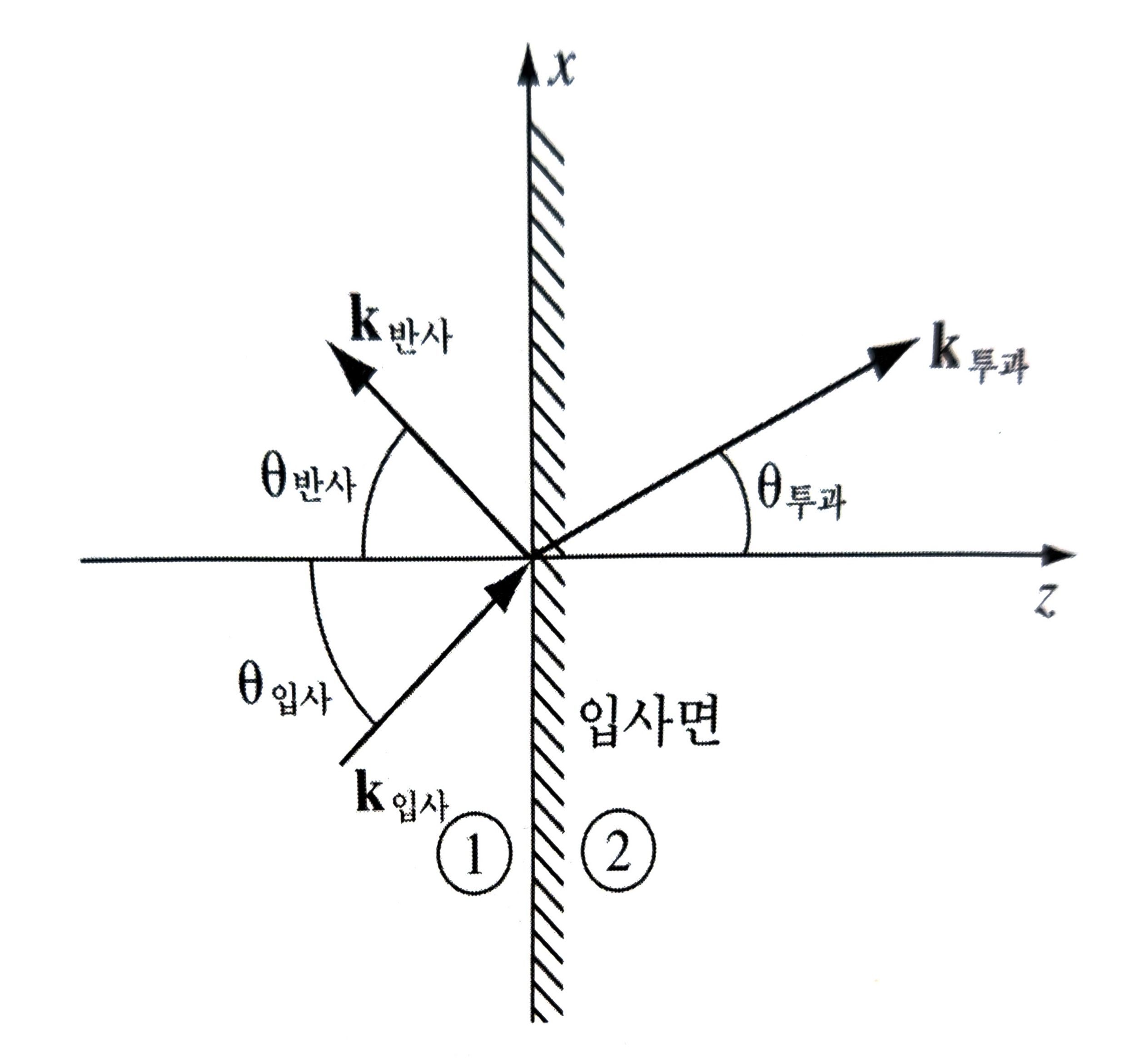
두 선형 매질이 \(z=0\)일 때 \(xy\) 평면에 평행하도록 맞닿아있고, 입사파의 진행 방항을 \(z\) 방향, 전기장이 \(x\) 방향과 나란하게 좌표계를 설정한다. 그때 입사파는 다음과 같다.

\[\tilde{\vec{E}}_{I}(z,t) = \tilde{E}_{I,0}e^{i(k_{1}z - \omega t)} \hat{x}, ~~~\tilde{\vec{B}}_{I}(z,t) = \frac{1}{v_{1}} \tilde{E}_{I,0}e^{i(k_{1}z - \omega t)}\hat{y}\]

반사파와 투과파의 진행 방향은 모두 z축과 나란하다. 또, 반사파와 투과파의 편광 방향은 입사파의 편광 방향과 나란하다.

[!question]- 왜 반사파와 투과파의 진행 방향이 z축과 나란한가?{title} 추후 증명할 반사 법칙과 스넬의 법칙을 사용한다.

\[\theta_{I}=\theta_{R}=0\] \[\frac{n_{1}}{n_{2}}=\frac{\sin \theta_{T}}{\sin \theta_{I}}\implies n_{1}\sin \theta_{I}=0=n_{2}\sin \theta_{T}\implies \theta_{T}=0\]

[!question]- 왜 반사파와 투과파의 편광 방향이 입사파의 편광 방향과 나란한가?{title} 편광 방향은 전기장 방향으로 결정된다. 반사파와 투과파의 편광 방향을 일반적으로 다음과 같이 설정하자. 이때 위 그림에서 \(\theta\)를 \(\phi\)라고 생각하라. 잘못 썼다.

\[\hat{n}_{R} = \cos \phi_{R}\hat{x} + \sin \phi_{R}\hat{y}\] \[\hat{n}_{T} = \cos \phi_{T}\hat{x} + \sin \phi_{T}\hat{y}\]

평면파이므로, 진행 방향과 전기장 자기장 방향은 모두 수직이므로, 전기장과 자기장의 \(z\) 성분은 고려하지 않는다. 따라서 반사파와 투과파의 일반해를 다음과 같이 쓸 수 있다.

\[\tilde{\vec{E}}_{R}(z,t) = \tilde{E}_{R,0}e^{i(-k_{1}z - \omega t)} \hat{n}_{R}, ~~\tilde{\vec{B}}_{R}(z,t) = \frac{1}{v_{1}}\tilde{E}_{R,0}e^{i(-k_{1}z - \omega t)} (-\hat{z}) \times \hat{n}_{R}\] \[\tilde{\vec{E}}_{T}(z,t) = \tilde{E}_{T,0}e^{i(k_{2}z-\omega t)}\hat{n}_{T}, ~~\tilde{\vec{B}}_{T}(z,t) = \frac{1}{v_{2}}e^{i(k_{2}z - \omega t)} \hat{z} \times \hat{n}_{T}\]

경계면과 수직인 성분은 \(z\) 성분이지만, \(z\) 성분이 없으므로 수직 Boundry Condition은 의미 없다. 따라서, 평행 Boundry Condition을 사용하자.

\[\vec{E}^\parallel_{1} = \vec{E}^\parallel_{2} \implies (\tilde{\vec{E}}_{I} + \tilde{\vec{E}}_{R})_{x,y} = (\tilde{\vec{E}}_{T})_{x,y}\]

이때, \(z=0\)이므로 지수항은 모두 상쇄된다.

\[\implies \tilde{E}_{I,0}\hat{x} + \tilde{E}_{R,0}\cos \phi_{R}\hat{x} + \tilde{E}_{R,0}\sin \phi_{R}\hat{y} = \tilde{E}_{T,0}\cos \phi_{T}\hat{x} + \tilde{E}_{T,0}\sin \phi_{T}\hat{y}\] \[\implies \begin{cases} \tilde{E}_{I,0} + \tilde{E}_{R,0}\cos \phi_{R} = \tilde{E}_{T,0}\cos \phi_{T} \\ \tilde{E}_{R,0}\sin \phi_{R} = \tilde{E}_{T,0}\sin \phi_{T} ~~ \dots ~~ (1) \end{cases}\]

자기장 평행 성분 Boundry Condition은 다음과 같다.

\[\frac{1}{\mu_{1}}\vec{B}^\parallel_{1} = \frac{1}{\mu_{2}}\vec{B}^\parallel_{2} \implies \frac{1}{\mu_{1}}(\tilde{\vec{B}}_{I} + \tilde{\vec{B}}_{R})_{x,y} = \frac{1}{\mu_{2}}(\tilde{\vec{B}}_{T})_{x,y}\] \[\implies \frac{1}{\mu_{1}}\left( \frac{1}{v_{1}}\tilde{E}_{I,0}\hat{y} + \frac{1}{v_{1}}\tilde{E}_{R,0} (-\hat{z}) \times \hat{n}_{R} \right)\] \[= \frac{1}{\mu_{2}} \left( \frac{1}{v_{2}} \tilde{E}_{T,0} \hat{z} \times \hat{n}_{T} \right)\] \[\implies \frac{1}{\mu_{1}v_{1}} (\tilde{E}_{I,0}\hat{y} - \tilde{E}_{R,0} (\hat{z} \times (\cos \phi_{R} \hat{x} + \sin \phi_{R} \hat{y})))\] \[= \frac{1}{\mu_{2}v_{2}}(\tilde{E}_{T,0}\hat{z} \times (\cos \phi_{T}\hat{x} + \sin \phi_{T}\hat{y}))\] \[\implies \frac{1}{\mu_{1}v_{1}}(\tilde{E}_{I,0}\hat{y} - \tilde{E}_{R,0}(\cos \phi_{R} \hat{y} - \sin \phi_{R} \hat{x}))\] \[= \frac{1}{\mu_{2}v_{2}} (\tilde{E}_{T,0} (\cos \phi_{T}\hat{y} - \sin \phi_{T} \hat{x}))\] \[\implies \begin{cases} \frac{1}{\mu_{1}v_{1}}\tilde{E}_{R,0}\sin \phi_{R} = -\frac{1}{\mu_{2}v_{2}} \tilde{E}_{T,0} \sin \phi_{T} ~~ \dots ~~ (2) \\ \frac{1}{\mu_{1}v_{1}}(\tilde{E}_{I_{0}} - \tilde{E}_{R,0}\cos \phi_{R}) = \frac{1}{\mu_{2}v_{2}}\tilde{E}_{T,0}\cos \phi_{T} \end{cases}\]

식 (1)과 (2)를 연립하면 다음과 같다.

\[\frac{1}{\mu_{1}v_{1}} \tilde{E}_{R,0} \sin \phi_{R} = - \frac{1}{\mu_{2}v_{2}} \tilde{E}_{R,0}\sin \phi_{R}\] \[\implies \left( \frac{1}{\mu_{1}v_{1}} + \frac{1}{\mu_{2}v_{2}} \right)\tilde{E}_{R,0}\sin \phi_{R} = 0\]

괄호 안의 값은 항상 양수이므로, 위 항등식을 만족하려면 \(\phi_{R}=0\)이어야 한다. (1) 식으로 인해 \(\phi_{T}=0\)까지 유도된다.

\[\phi_{R} = \phi_{T} = 0\]

반사파와 투과파의 편광 방향은 입사파와 나란하다.

즉, 일반해는 다음과 같다.

\[\tilde{\vec{E}}_{I}(z,t) = \tilde{E}_{I,0}e^{i(k_{1}z - \omega t)} \hat{x}, ~~~\tilde{\vec{B}}_{I}(z,t) = \frac{1}{v_{1}} \tilde{E}_{I,0}e^{i(k_{1}z - \omega t)}\hat{y}\] \[\tilde{\vec{E}}_{R}(z,t) = \tilde{E}_{R,0}e^{i(-k_{1}z - \omega t)} \hat{x}, ~~~\tilde{\vec{B}}_{R}(z,t) = -\frac{1}{v_{1}} \tilde{E}_{R,0}e^{i(-k_{1}z - \omega t)}\hat{y}\] \[\tilde{\vec{E}}_{T}(z,t) = \tilde{E}_{T,0}e^{i(k_{2}z - \omega t)} \hat{x}, ~~~\tilde{\vec{B}}_{T}(z,t) = \frac{1}{v_{2}} \tilde{E}_{T,0}e^{i(k_{2}z - \omega t)}\hat{y}\]

평행 성분의 Boundry Condition을 사용하여, 계수 간의 관계를 유도해보자.

\[\vec{E}^{\parallel}_{1} = \vec{E}^{\parallel}_{2}\implies (\tilde{\vec{E}}_{I} + \tilde{\vec{E}}_{R})_{z} = (\tilde{\vec{E}}_{T})_{z}\] \[\implies \tilde{E}_{I,0} + \tilde{E}_{R,0} = \tilde{E}_{T,0}\]

자기장의 평행 성분 바운더리 컨디션을 사용해보자.

\[\vec{H}^{\parallel}_{1} = \vec{H}^{\parallel}_{2}\implies \left( \frac{1}{\mu_{1}}\vec{B}^{\parallel}_{1} = \frac{1}{\mu_{2}}\vec{B}^{\parallel}_{2} \right)\] \[\implies \frac{1}{\mu_{1}}\left( \frac{1}{v_{1}}\tilde{E}_{I,0}e^{-i\omega t}\hat{y} - \frac{1}{v_{1}}\tilde{E}_{R,0}e^{-i\omega t}\hat{y} \right) = \frac{1}{\mu_{2}}\left( \frac{1}{v_{2}}\tilde{E}_{T,0}e^{-i\omega t} \hat{y}\right)\] \[\implies \frac{1}{\mu_{1}v_{1}}(\tilde{E}_{I,0} - \tilde{E}_{R,0}) = \frac{1}{\mu_{2}v_{2}}\tilde{E}_{T,0}\] \[\implies \tilde{E}_{I,0} - \tilde{E}_{R,0} = \frac{\mu_{1}v_{1}}{\mu_{2}v_{2}} \tilde{E}_{T,0}\]

이때, \(\beta\)를 다음과 같이 정의하자.

\[\beta \equiv \frac{\mu_{1}v_{1}}{\mu_{2}v_{2}} = \frac{\mu_{1}n_{2}}{\mu_{2}n_{1}} ~~\left( n \propto \frac{1}{v} \right)\] \[\tilde{E}_{I,0} - \tilde{E}_{R,0} = \beta \tilde{E}_{T,0}\]

연립 방정식을 세워서 반사 계수와 투과 계수를 입사 계수로 표현하면 다음과 같다.

\[2\tilde{E}_{I,0} = (1+\beta)\tilde{E}_{T,0} \implies \tilde{E}_{T,0} = \left( \frac{2}{1+\beta} \right)\tilde{E}_{I,0}\] \[\tilde{E}_{I,0} + \tilde{E}_{R,0} = \left( \frac{2}{1+\beta} \right)\tilde{E}_{I,0} \implies \tilde{E}_{R,0} = \left( \frac{1-\beta}{1+\beta} \right)\tilde{E}_{I,0}\]

어차피 대부분의 매질의 \(\mu\)는 비슷 하므로, \(\beta\)를 \(\frac{v_{1}}{v_{2}}\)로 근사할 수 있다. 따라서, \(\beta\) 대신 다음과 같이 쓸 수 있다.

\[\tilde{E}_{T,0} = \left( \frac{2}{1+ \frac{v_{1}}{v_{2}}} \right)\tilde{E}_{I,0} = \left( \frac{2v_{2}}{v_{1}+v_{2}} \right) \tilde{E}_{I,0}\] \[\tilde{E}_{R,0}= \left( \frac{1- \frac{v_{1}}{v_{2}}}{1+ \frac{v_{1}}{v_{2}}} \right) \tilde{E}_{I,0} = \left( \frac{\frac{v_{2}-v_{1}}{v_{1}+v_{2}}}{\frac{v_{2}+v_{1}}{v_{1}+v_{2}}} \right) \tilde{E}_{I,0} = \left( \frac{v_{2}-v_{1}}{v_{1}+v_{2}} \right)\tilde{E}_{I,0}\]

이를 굴절율로 쓰면 다음과 같다.

\[\tilde{E}_{T,0} = \left( \frac{2n_{1}}{n_{1}+n_{2}} \right)\tilde{E}_{I,0}\] \[\tilde{E}_{R,0}=\left( \frac{n_{1}-n_{2}}{n_{1}+n_{2}} \right)\tilde{E}_{I,0}\]

\(\tilde{E}_{I,0}=E_{I,0}e^{i\delta_{I}}, ~ \tilde{E}_{T,0}=E_{T,0}e^{i\delta_{T}}, ~\tilde{E}_{R,0}=E_{R,0}e^{i\delta_{R}}\)로 쓸 수 있다. 복소수의 길이(진폭)와 위상이 각각 같아야 하고, \(v_{2}>v_{1}\)이면 반사파와 입사파의 위상이 같다.

\[\delta_{I} = \delta_{R}\]

\(v_{1}<v_{2}\)면, 길이 부분이 마이너스이므로, 같아지려면 \(-1=e^{i\pi}\)를 사용하여 음수를 위상으로 보내야 한다. 따라서 진폭은 같고 위상은 \(\pi\)만큼 차이난다.

\[\delta_{I} = \delta_{R} + \pi\]

반사파와 투과파의 세기는 어떻게 분배가 될까? 단색 평면파의 세기는 다음과 같다.

\[I= \lvert \langle\vec{S} \rangle \rvert = \frac{1}{2}\epsilon_{0}vE_{0}^2\]

반사율(reflectance) 를 다음과 같이 정의한다.

\[R\equiv \frac{I_{R}}{I_{I}} = \frac{\frac{1}{2}\epsilon_{1}v_{1}E_{R,0}^2}{\frac{1}{2}\epsilon_{1}v_{1}E_{I,0}^2} = \left( \frac{E_{R,0}}{E_{I,0}} \right)^2 = \left( \frac{n_{1} - n_{2}}{n_{1} + n_{2}} \right)^2\]

투과율(transmittance) 를 다음과 같이 정의한다.

\[T \equiv \frac{I_{T}}{I_{I}} = \frac{\frac{1}{2}\epsilon_{2}v_{2}E_{T,0}^2}{\frac{1}{2}\epsilon_{1}v_{1}E_{I,0}^2} = \frac{\epsilon_{2}v_{2}}{\epsilon_{1}v_{1}} \left( \frac{E_{T,0}}{E_{I,0}} \right)^2\]

이때 계수는 다음과 같다.

\[\frac{\epsilon_{2}v_{2}}{\epsilon_{1}v_{1}} = \frac{\epsilon_{2} \sqrt{ \frac{1}{\epsilon_{2}\mu_{2}} }}{\epsilon_{1} \sqrt{ \frac{1}{\epsilon_{1}\mu_{1}} }} = \frac{\frac{1}{\mu_{2}} \sqrt{ \epsilon_{2}\mu_{2} }}{\frac{1}{\mu_{1}}\sqrt{ \epsilon_{1}\mu_{1} }} = \frac{\mu_{1}v_{1}}{\mu_{2}v_{2}} = \frac{\mu_{1} n_{2}}{\mu_{2} n_{1}}\]

제곱항은 다음과 같다.

\[\left( \frac{E_{T,0}}{E_{I,0}} \right)^2 = \left( \frac{2n_{1}}{n_{1}+n_{2}} \right)^2 = \frac{4n_{1}^2}{(n_{1}+n_{2})^2}\]

따라서 다음과 같다.

\[T = \frac{\mu_{1}n_{2}}{\mu_{2}n_{1}} \cdot \frac{4n_{1}^2}{(n_{1}+n_{2})^2} \simeq \frac{4n_{1}n_{2}}{(n_{1}+n_{2})^2}\]

반사율과 투과율은 다음 관계식을 따른다.

\[R+T = \frac{(n_{1} - n_{2})^2}{(n_{1}+n_{2})^2} + \frac{4n_{1}n_{2}}{(n_{1}+n_{2})^2} = \frac{(n_{1}+n_{2})^2}{(n_{1}+n_{2})^2} = 1\]

[!question]- 만약 \(\mu\)를 근사하지 않으면 \(T\)에 \(\frac{\mu_{1}}{\mu_{2}}\) 항이 남아서 \(R+T=1\)가 안되는 것 아닌가?{title} 애초에 위에서 전기장 진폭의 \(\beta\)를 \(\frac{v_{1}}{v_{2}}\)로 근사했기 때문에 오류가 있는 것처럼 보이는 것이다.

\(\mu\)를 근사하지 않을거면, \(\beta= \frac{\mu_{1}v_{1}}{\mu_{2}v_{2}}\)를 그대로 사용해야하고, 근사할거면 계속 근사해야 일관성이 유지된다.

진짜 \(\mu_{1} \simeq \mu_{2}\)로 근사하지 않아도 \(R+T=1\)이 유도될까?

\[\tilde{E}_{R,0} = \left( \frac{1-\beta}{1+\beta} \right) \tilde{E}_{I,0} ~~~~~\tilde{E}_{T,0} = \left( \frac{2}{1+\beta} \right) \tilde{E}_{I,0} ~~~~~\beta = \frac{\mu_{1}v_{1}}{\mu_{2}v_{2}}\] \[R = \frac{I_{R}}{I_{I}} = \frac{\frac{1}{2}\epsilon_{1}v_{1} E_{R,0}^2}{\frac{1}{2} \epsilon_{1}v_{1} E_{I,0}^2} = \left( \frac{1-\beta}{1+\beta} \right)^2\] \[T = \frac{I_{T}}{I_{I}} = \frac{\frac{1}{2}\epsilon_{2}v_{2}E_{T,0}^2}{\frac{1}{2}\epsilon_{1}v_{1}E_{I,0}^2} = \frac{\epsilon_{2}v_{2}}{\epsilon_{1}v_{1}} \left( \frac{E_{T,0}}{E_{I,0}} \right)^2 = \beta \cdot \frac{4}{(1+\beta)^2}\] \[R+T = \left( \frac{1-\beta}{1+\beta} \right)^2 + \frac{4\beta}{(1+\beta)^2} = \frac{(1+\beta)^2}{(1+\beta)^2} = 1\]

두 유전체 경계에 단색 평면파를 비스듬히 입사시키면?

수직 입사는 \(\theta_{I}=0\)인 특별한 경우와 같다. 더 일반적으로, 입사각 \(\theta_{I}\)가 존재하면 어떻게 될까? 일반적인 입사파, 반사파, 투과파의 해는 다음과 같다.

\[\tilde{\vec{E}}_{I}(\vec{r},t) = \tilde{\vec{E}}_{I,0}e^{i(\vec{k}_{I} \cdot \vec{r} - \omega t)}, ~~\tilde{\vec{B}_{I}} = \frac{1}{v_{1}} \vec{k}_{I} \times \tilde{\vec{E}_{I}}\] \[\tilde{\vec{E}}_{R}(\vec{r},t) = \tilde{\vec{E}}_{R,0}e^{i(\vec{k}_{R} \cdot \vec{r} - \omega t)}, ~~\tilde{\vec{B}_{R}} = \frac{1}{v_{1}} \vec{k}_{R} \times \tilde{\vec{E}_{R}}\] \[\tilde{\vec{E}}_{T}(\vec{r},t) = \tilde{\vec{E}}_{T,0}e^{i(\vec{k}_{T} \cdot \vec{r} - \omega t)}, ~~\tilde{\vec{B}_{T}} = \frac{1}{v_{2}} \vec{k}_{T} \times \tilde{\vec{E}_{T}}\]

모두 단색 평면파이기 때문에, 일반해 모양은 동일하다. 이제 Boundry Condition을 사용하여 \(\vec{k}\), 계수 등을 찾아내면 된다.

(1) 한 순간에서 세 파동의 입사면에서 위상이 모두 같아야 한다. 입사면을 \(z=0\) 평면, 즉 xy평면으로 설정하자. 입사 파동, 반사 파동, 투과 파동의 위상은 입사면에서 모두 같아야 한다. 그렇지 않으면, 파동이 불연속적으로 툭 끊기게 되는데, 이는 물리적으로 가능하지 않다고 보기 때문이다.

파동의 위상이 무엇인가? 예를 들어, 실수 파동 \(\cos(kx - \omega t + \phi)\)에서 \(kx\)는 위치에 따라 위상이 어떻게 변하는지에 대한 항, \(\omega t\)는 시간에 따라 위상이 어떻게 변하는지에 대한 항, \(\phi\)는 초기 위상 값과 같다. 즉, 파동의 총 위상은 코사인에 들어가는 전체를 의미한다.

\(z=0\)에서 입사파, 반사파, 투과파의 위상이 같아야 하므로 다음이 성립해야 한다.

\[(\vec{k}_{I} \cdot \vec{r} - \omega t)_{z=0} = (\vec{k}_{R} \cdot \vec{r} - \omega t)_{z=0} = (\vec{k}_{T} \cdot \vec{r} - \omega t)_{z=0}\] \[\implies (\vec{k}_{I} \cdot \vec{r})_{z=0} = (\vec{k}_{R} \cdot \vec{r})_{z=0} = (\vec{k}_{T} \cdot \vec{r})_{z=0}\] \[\implies (k_{I})_{x}\hat{x} + (k_{I})_{y} \hat{y} = (k_{R})_{x}\hat{x} + (k_{R})_{y} \hat{y} = (k_{T})_{x}\hat{x} + (k_{T})_{y} \hat{y}\] \[(k_{I})_{x} = (k_{R})_{x} = (k_{T})_{x}, ~~~~(k_{I})_{y} = (k_{R})_{y} = (k_{T})_{y}\]

위와 같은 조건을 유도해낼 수 있다. 우리는 좌표축을 설정할 수 있는 자유도를 가지고 있고, 입사파의 y 성분을 0으로 만드는 좌표계를 설정할 수 있다. 따라서 다음과 같다.

\[0 = (k_{I})_{y} = (k_{R})_{y} = (k_{T})_{y}\]

따라서, \(\vec{k}_{I}, \vec{k}_{R}, \vec{k}_{T}\)는 한 평면 위에 존재한다. 그 평면을 입사면(plane of incidence) 이라 하자. 이 경우 입사면은 xz 평면이다.

\(\vec{k}\) 벡터의 \(x\) 성분이 모두 같아야 하므로, 다음과 같다.

\[k_{I}\sin \theta_{I} = k_{R}\sin \theta_{R} = k_{T}\sin \theta_{T}\]

그리고, 세 파동의 \(\omega\)는 모두 같으므로, 다음과 같다.

\[\omega = k_{I}v_{1} = k_{R}v_{1} = k_{T}v_{2} \implies k_{I} = k_{R} = \frac{v_{2}}{v_{1}}k_{T} = \frac{n_{1}}{n_{2}} k_{T}\]

따라서, 입사각과 반사각은 항상 같음을 알 수 있다.

\[k_{I}\sin \theta_{I} = k_{R}\sin \theta_{R} \implies \sin \theta_{I} = \sin \theta_{R} \implies \theta_{I} = \theta_{R}\]

이를 반사 법칙(law of reflection) 라고 한다.

또, 입사각과 투과각은 굴절율과 관계있음을 알 수 있다.

\[k_{I}\sin \theta_{I} = k_{T}\sin \theta_{T} \implies \frac{n_{1}}{n_{2}}\sin \theta_{I} = \sin \theta_{T} \implies \frac{n_{1}}{n_{2}}= \frac{\sin \theta_{T}}{\sin \theta_{I}}\]

이를 굴절 법칙(law of refraction), 스넬 법칙(Snell’s law) 라고 한다.

결론적으로, 경계면에서 위상이 같아야 한다는 경계조건으로 세가지 법칙이 유도된다.

1. 입사파, 반사파, 투과파의 \(\vec{k}\) 벡터는 같은 평면에 있다. 이를 입사면이라고 한다.
2. 입사각과 반사각은 같다.
3. 입사각과 투과각의 sin 비는, 굴절율 비의 역수와 같다.

(2) 맥스웰 방정식의 경계조건 자유전하, 전류가 없는 경우 매질 속 맥스웰 방정식은 다음과 같다.

\[\nabla \cdot \vec{D} = 0, ~~\nabla \cdot \vec{B} = 0, ~~\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}, ~~\nabla \times \vec{H} = \frac{\partial \vec{D}}{\partial t}\]

각각의 식으로부터 유도되는 경계 조건은 다음과 같다.

\[D^\bot_{1} = D_{2}^\bot, ~~B^\bot_{1} = B^\bot_{2}, ~~\vec{E}^\parallel_{1} = \vec{E}^\parallel_{2}, ~~\vec{H}^\parallel_{1} = \vec{H}^\parallel_{2}\] \[\implies \epsilon_{1}E^\bot_{1} = \epsilon_{2}E^\bot_{2}, ~~B^\bot_{1} = B^\bot_{2}, ~~\vec{E}^\parallel_{1} = \vec{E}^\parallel_{2}, ~~\frac{1}{\mu_{1}}\vec{B}^\parallel_{1} = \frac{1}{\mu_{2}}\vec{B}^\parallel_{2}\]

\(z\)성분이 경계면과 수직이고, \(x,y\)성분이 경계면과 평행한 성분이므로 다음과 같다.

\[\epsilon_{1}(\tilde{\vec{E}}_{I,0} + \tilde{\vec{E}}_{R,0})_{z} = \epsilon_{2}(\tilde{\vec{E}}_{T,0})_{z}\] \[(\tilde{\vec{B}}_{I,0} + \tilde{\vec{B}}_{R,0})_{z} = (\tilde{\vec{B}}_{T,0})_{z}\] \[(\tilde{\vec{E}}_{I,0} + \tilde{\vec{E}}_{R,0})_{x,y} = (\tilde{\vec{E}}_{T,0})_{x,y}\] \[\frac{1}{\mu_{1}}(\tilde{\vec{B}}_{I,0} + \tilde{\vec{B}}_{R,0})_{x,y} = \frac{1}{\mu_{2}} (\tilde{\vec{B}}_{T,0})_{x,y}\]

1. 입사점을 원점으로 설정하면, \(\vec{r} = \vec{0}\)이다. 시간도 모두 동시므로 \(e^{i(\vec{k} \cdot \vec{r} - \omega t)}\)항을 상쇄할 수 있다.
2. y성분이 0인건 \(\vec{k}\)에만 해당한다. \(\vec{E}\)와 \(\vec{B}\)는 y성분이 존재할 수 있기 떄문에, 경계면과 평행한 성분으로 \(x, y\) 둘다 고려해야 한다.

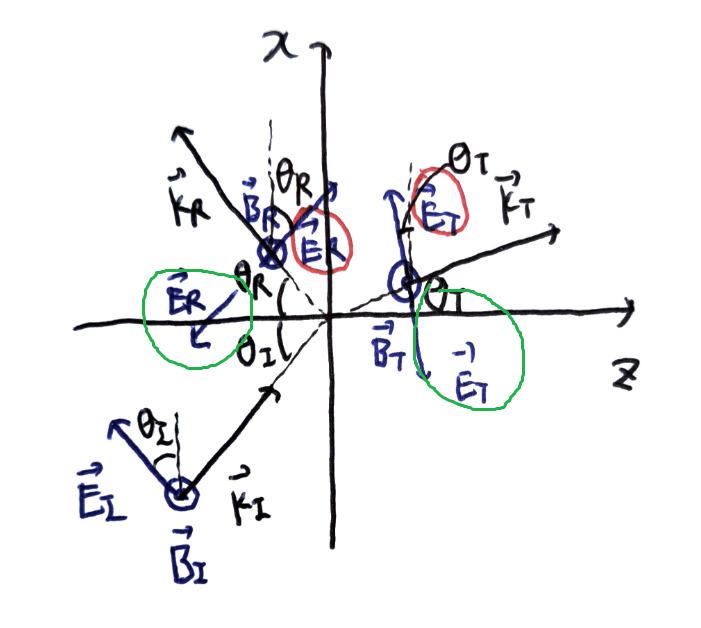
이때, 두가지 Case를 고려할 수 있다. (Case I) \(\vec{E}_{I}\)가 입사면과 평행한 경우 이는 \((\vec{E}_{I,0})_{y} = 0\), \((\vec{B}_{I,0})_{x,z}=0\)인 경우와 같다. 이 경우, 입사파, 반사파, 투과파의 편광 벡터가 한 평면 위에 존재한다.

[!question]- 왜 세 파동의 편광 벡터가 한 평면 위에 존재하는가?{title} 세번째 바운더리 컨디션에서 다음 조건을 뽑아낸다.

\[(\tilde{\vec{E}}_{R,0})_{y} = (\tilde{\vec{E}}_{T,0})_{y}\]

네번째 바운더리 컨디션에서 다음 조건을 뽑아낸다.

\[\frac{1}{\mu_{1}}(\tilde{\vec{B}}_{R,0})_{x} = \frac{1}{\mu_{2}}(\tilde{\vec{B}}_{T,0})_{x}\] \[\implies \frac{1}{\mu_{1}}\left( \frac{1}{v_{1}} \hat{k}_{R} \times \tilde{\vec{E}}_{R,0} \right)_{x} = \frac{1}{\mu_{2}} \left( \frac{1}{v_{2}} \hat{k}_{T} \times \tilde{\vec{E}}_{T,0} \right)_{x}\]

\(\tilde{\vec{E}}_{R,0}\)과 \(\tilde{\vec{E}}_{T,0}\)은 x,y,z 성분이 모두 있다고 가정한다. \(\hat{k}_{R}\)는 \(\sin \theta_{R}\hat{x} - \cos \theta_{R} \hat{z}\)와 같고, \(\hat{k}_{T}\)는 \(\sin \theta_{T}\hat{x} + \cos \theta_{R}\hat{z}\)과 같다. \(y, z\) 성분을 외적해야 \(x\)성분이 나온다. \(\hat{z} \times \hat{y} = -\hat{x}\)이므로, 다음과 같다.

\[\frac{1}{\mu_{1}v_{1}}\left( -\cos \theta_{R}(\tilde{\vec{E}}_{R,0})_{y}(-\hat{x}) \right) = \frac{1}{\mu_{2}v_{2}}\left(\cos \theta_{T} (\tilde{\vec{E}}_{T,0})_{y}\hat{k}_{T,z} \right)\] \[\implies \frac{\cos \theta_{R}}{\mu_{1}v_{1}} (\tilde{\vec{E}}_{R,0})_{y} + \frac{\cos \theta_{T}}{\mu_{2}v_{2}}(\tilde{\vec{E}}_{T,0})_{y} = 0\]

위 항등식이 성립하려면 \((\tilde{\vec{E}}_{R,0})_{y} = (\tilde{\vec{E}}_{T,0})_{y} = 0\)이거나, 다음 관계를 만족해야 한다.

\[\frac{\cos \theta_{R}}{\mu_{1}v_{1}} + \frac{\cos \theta_{T}}{\mu_{2}v_{2}}= 0\]

\(\mu v\)는 양수값이다. 위 항등식이 만족하려면, 둘 중 하나의 \(\cos\) 값이 음수값이 되어야 한다. 그러나, 각도의 범위는 다음과 같이 제한된다.

\[0 < \theta_{R} < \frac{\pi}{2}, ~~0 < \theta_{T} < \frac{\pi}{2}\]

각도가 0이면 위에서 다룬 경계면에 수직으로 입사시키는 상황이므로 고려하지 않고, \(\frac{\pi}{2}\) 이상인 경우는 당연히 고려대상이 아니다. 위 범위에서 코사인 값은 항상 양수값이다. 즉 위 항등식은 비스듬히 입사하는 경우에는 성립될 수 없다. 따라서 모순이며, 바운더리 컨디션을 만족하기 위해서는 다음 조건이 성립되어야 한다.

\[(\tilde{\vec{E}}_{R,0})_{y} = (\tilde{\vec{E}}_{T,0})_{y} = 0\]

반사파와 투과파 편광 벡터의 \(y\)성분이 존재하지 않는다. 입사파, 반사파, 투과파의 모든 편광 벡터는 같은 입사평면 위에 존재해야 한다는 사실을 발견한다.

편광벡터는 \(\vec{k}\)와 수직이어야 하고, 입사평면 위에 존재해야 한다. 두 조건을 만족하는 편광 벡터의 가능성이 각각 두가지가 존재한다. 둘 중 임의의 한 방향을 선택한다. 임의의 방향을 선택해도 나중에 유도된 결과의 물리적 의미는 동일하다.

Boundry Condition을 사용하여 진폭 상수간의 관계를 유도하자.

\[\epsilon_{1}(\tilde{\vec{E}}_{I,0} + \tilde{\vec{E}}_{R,0})_{z} = \epsilon_{2}(\tilde{\vec{E}}_{T,0})_{z}\] \[\implies \epsilon_{1}(-\tilde{E}_{I,0}\sin \theta_{I} + \tilde{E}_{R,0} \sin \theta_{R}) = \epsilon_{2}(-\tilde{E}_{T,0}\sin \theta_{T})\] \[(\tilde{\vec{B}}_{I,0} + \tilde{\vec{B}}_{R,0})_{z} = (\tilde{\vec{B}}_{T,0})_{z}\]

자기장의 \(z\) 성분은 없으므로, 의미 없다.

\[(\tilde{\vec{E}}_{I,0} + \tilde{\vec{E}}_{R,0})_{x,y} = (\tilde{\vec{E}}_{T,0})_{x,y}\] \[\implies \tilde{E}_{I,0}\cos \theta_{I} + \tilde{E}_{R,0}\cos \theta_{R} = \tilde{E}_{T,0}\cos \theta_{T}\] \[\implies \tilde{E}_{I,0} + \tilde{E}_{R,0} = \frac{\cos \theta_{T}}{\cos \theta_{I}} \tilde{E}_{T,0} \equiv \alpha \tilde{E}_{T,0}\] \[\frac{1}{\mu_{1}}(\tilde{\vec{B}}_{I,0} + \tilde{\vec{B}}_{R,0})_{x,y} = \frac{1}{\mu_{2}} (\tilde{\vec{B}}_{T,0})_{x,y}\] \[\implies \frac{1}{\mu_{1}}(\tilde{B}_{I,0} - \tilde{B}_{R,0}) = \frac{1}{\mu_{2}}(\tilde{B}_{T,0})\] \[\implies \frac{1}{\mu_{1}v_{1}}(\tilde{E}_{I,0} - \tilde{E}_{R,0}) = \frac{1}{\mu_{2}v_{2}} (\tilde{E}_{T,0})\] \[\implies \tilde{E}_{I,0} - \tilde{E}_{R,0} = \frac{\mu_{1}v_{1}}{\mu_{2}v_{2}}\tilde{E}_{T,0} \equiv \beta \tilde{E}_{T,0}\]

두 식을 연립하면 다음과 같다.

\[2\tilde{E}_{I,0} = (\alpha + \beta)\tilde{E}_{T,0} \implies \tilde{E}_{T,0} = \left( \frac{2}{\alpha + \beta} \right) \tilde{E}_{I,0}\] \[\tilde{E}_{I,0} + \tilde{E}_{R,0} = \frac{2\alpha}{\alpha+\beta}\tilde{E}_{I,0} \implies \tilde{E}_{R,0} = \left( \frac{\alpha-\beta}{\alpha+\beta} \right)\tilde{E}_{I,0}\]

위 두 진폭 관계가 편광방향이 입사면과 나란할 때의 프레넬 공식(Fresnel’s equation) 이다. 위상을 생각해보자.

\[\tilde{E}_{I,0} = E_{I,0}e^{i \delta_{I}}, ~~\tilde{E}_{R,0} = E_{R,0}e^{i \delta_{R}}, ~~\tilde{E}_{T,0} = E_{T,0}e^{i \delta_{T}}\]

투과파의 위상은 입사파와 동일하다. 입사파와 반사파는 \(\alpha>\beta\)일 경우 위상이 같고, \(\alpha<\beta\)일 경우 위상이 \(\pi\)만큼 차이난다.

[!question]- 만약 편광 방향을 다르게 잡으면 어떤 결과가 나올까?{title}

편광 벡터의 방향을 초록색으로 표시한 방향으로 잡아보자. 똑같이 유도하면, 다음과 같은 프레넬 방정식을 얻는다.

\[\tilde{E}_{R,0} = \left( \frac{\beta-\alpha}{\alpha+\beta} \right)\tilde{E}_{I,0}\] \[\tilde{E}_{T,0} = \left( - \frac{2}{\alpha+\beta} \right)\tilde{E}_{I,0}\]

투과파와 입사파의 위상이 동일하다는 결과와, \(\beta-\alpha\) 부호에 따라 위상 차이나는 결과가 기존 프레넬 방정식과 동일하다. 따라서, 편광 벡터의 방향을 아무 방향이나 잡아도 프레넬 방정식의 부호 차이만 있을 뿐 물리적 의미는 동일하다.

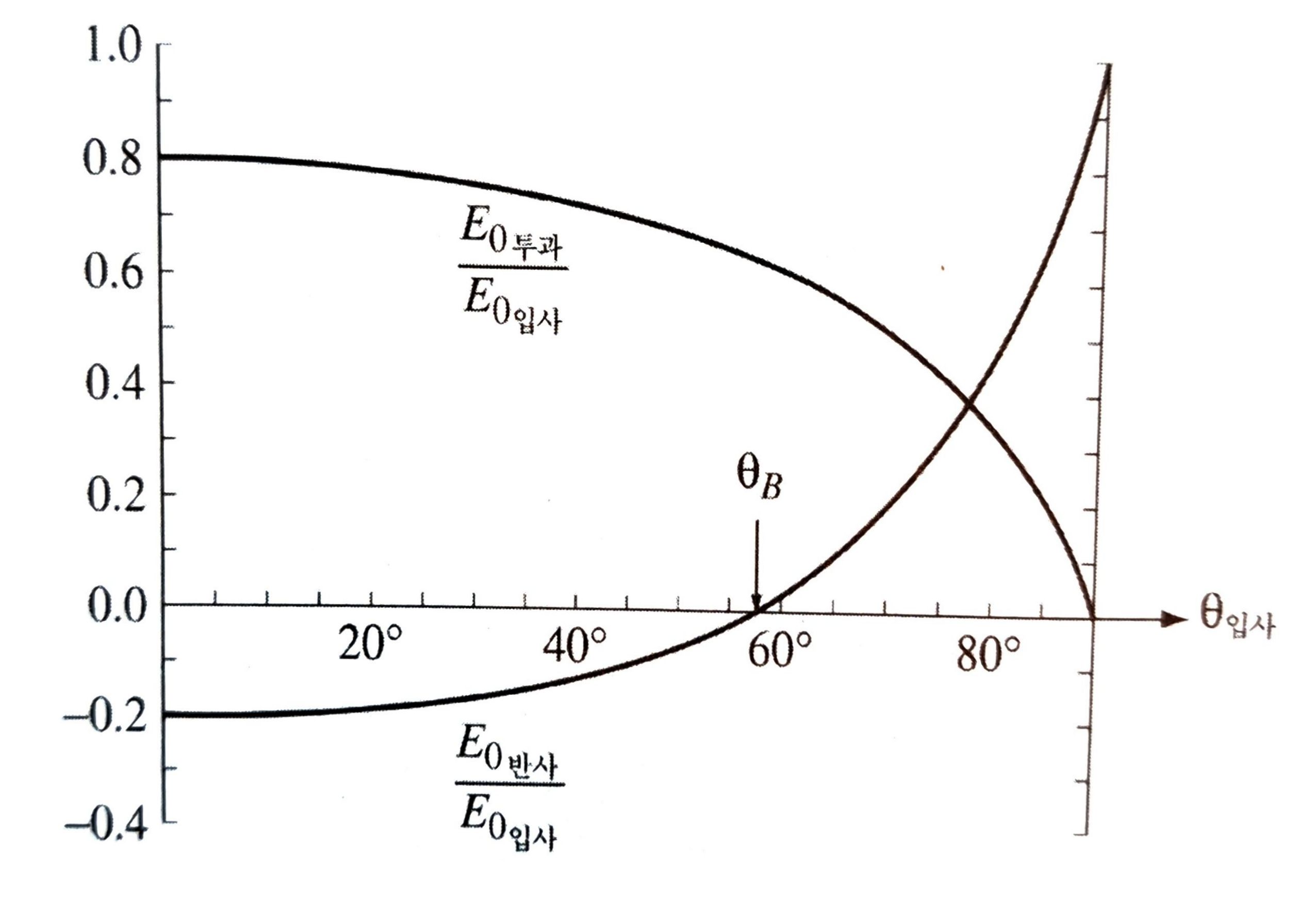
그렇다면, \(\alpha = \beta\)가 되면 어떻게 될까? 결론적으로, 반사파가 생기지 않고 모두 투과된다. 그때의 입사각 각도를 브루스터 각(Brewster’s angle) \(\theta_{B}\)라고 하며, 다음과 같다.

\[\tan \theta_{B} \simeq \frac{n_{2}}{n_{1}}\]

[!question]- 브루스터 각이 왜 굴절율로 결정되는가?{title} \(\alpha = \beta\)일 때, 반사파의 계수가 0이므로 투과파만 존재한다. 이 조건을 어떻게 만들 수 있을까? \(\alpha\)는 투과각과 입사각에 의존하며, 스넬의 법칙을 사용하여 입사각에 대한 함수로 표현할 수 있다.

\[\alpha = \frac{\cos \theta_{T}}{\cos \theta_{I}} = \frac{\sqrt{ 1-\sin^2 \theta_{T} }}{\cos \theta_{I}} = \frac{\sqrt{ 1- \left( \frac{n_{1}}{n_{2}} \right)^2\sin^2\theta_{I} }}{\cos \theta_{I}}=\alpha(\theta_{I})\]

즉, \(\theta_{I}\)를 잘 조절해서 \(\alpha = \beta\) 상황을 만들 수 있을 것 같다. 그때의 입사각을 브루스터 각(Brewster’s angle) \(\theta_{B}\)라고 하자. \(\theta_{B}\)의 조건은 다음과 같다.

\[\alpha(\theta_{B}) = \beta \implies \frac{\sqrt{ 1- \left( \frac{n_{1}}{n_{2}} \right)^2 \sin^2\theta_{B} }}{\cos \theta_{B}} = \beta\] \[\implies 1-\left( \frac{n_{1}}{n_{2}} \right)^2 \sin^2\theta_{B} = \beta^2 \cos^2\theta_{B}\] \[\implies 1-\left( \frac{n_{1}}{n_{2}} \right)^2\sin^2\theta_{B} = \beta^2(1-\sin^2\theta_{B})\] \[\implies \left( \left( \frac{n_{1}}{n_{2}} \right)^2 - \beta^2 \right)\sin^2\theta_{B} = 1-\beta^2\] \[\implies \sin^2\theta_{B} = \frac{1-\beta^2}{\left( \frac{n_{1}}{n_{2}} \right)^2 - \beta^2}\]

이때 \(\beta\)를 \(\frac{v_{1}}{v_{2}}=\frac{n_{2}}{n_{1}}\)로 근사하면, \(\left( \frac{n_{1}}{n_{2}} \right)^2 \simeq \frac{1}{\beta^2}\)로 쓸 수 있다.

\[\implies \sin^2\theta_{B} \simeq \frac{1-\beta^2}{\frac{1}{\beta^2}-\beta^2} = \frac{1-\beta^2}{\frac{1-\beta^4}{\beta^2}} = \frac{\beta^2}{1+\beta^2}\] \[\cos^2\theta_{B} = 1-\sin^2\theta_{B} \simeq \frac{1}{1+\beta^2}\] \[\tan \theta_{B} \simeq \sqrt{ \frac{\frac{\beta^2}{1+\beta^2}}{\frac{1}{1+\beta^2}} } = \beta = \frac{n_{2}}{n_{1}}\] \[\implies \theta_{B} \simeq \tan^{-1}\left( \frac{n_{2}}{n_{1}} \right)\]

예를들어, 빛이 공기 \(n_{1}=1\)에서 유리 \(n_{2}=1.5\)로 입사하면, 그때의 대략적인 \(\theta_{B}\)는 다음과 같다.

\[\theta_{B} = \tan^{-1}(1.5) \simeq 56.3 ^\circ\]

투과진폭과 반사진폭의 입사파에 대한 비를 입사파에 대한 함수로 나타낸 그래프는 아래와 같다.

각 전자기파의 세기는 다음과 같다.

\[I = \langle \vec{S} \cdot \hat{z} \rangle\]

[!question] 왜 \(I\)가 포인팅 벡터의 내적인가? 그냥 포인팅 벡터 크기의 평균 아니었나?{title} 두 매질의 경계면에서 에너지 보존 법칙은 \(R+T=1\)로 설명된다. 이때 반사율 \(R\)은 경계면에 입사하는 에너지 흐름 대비, 반사되는 에너지 흐름의 비율과 같다. 투과율 \(T\)는 경계면에 입사하는 에너지 흐름 대비, 투과되는 에너지 흐름의 비율과 같다. 에너지 흐름은 포인팅 벡터 \(\vec{S}\)와 같고, 경계면을 통과하는 에너지 흐름은, \(\vec{S} \cdot \hat{n}\)과 같다. 경계면의 평행한 성분은 경계를 통과하지 않으므로, 에너지 보존 법칙에 고려하지 않는다. 따라서, \(I\)를 다음과 같이 정의한다.

각 전자기파의 \(I\)는 다음과 같다.

\[I_{I} = \frac{1}{2}\epsilon_{1}v_{1}E_{I,0}^2\cos \theta_{I}\] \[I_{R} = \frac{1}{2}\epsilon_{1}v_{1}E_{R,0}^2\cos \theta_{R}\] \[I_{T} = \frac{1}{2}\epsilon_{2}v_{2}E_{T,0}^2\cos \theta_{T}\]

반사율 \(R\)과 투과율 \(T\)는 다음과 같다.

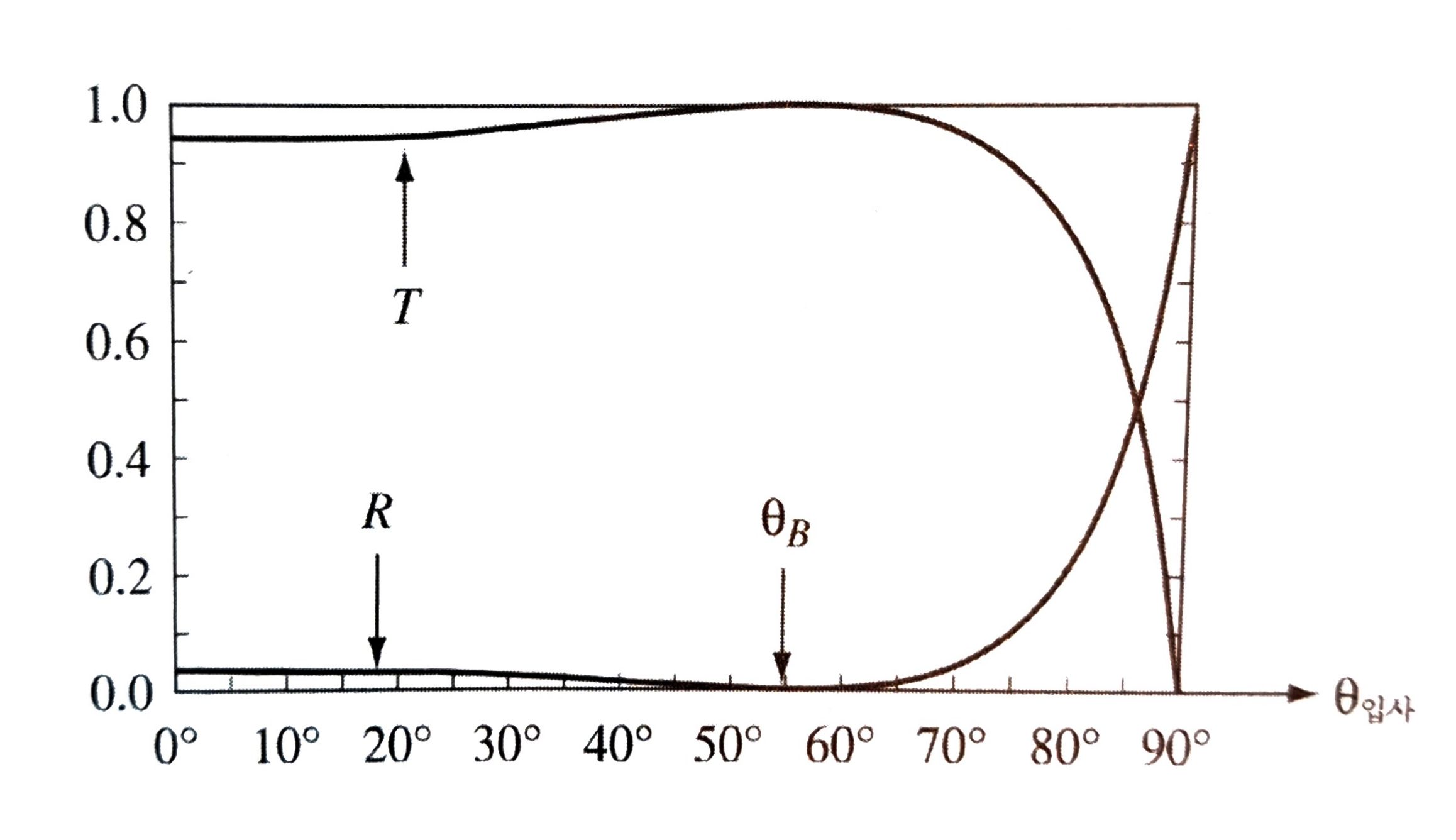
\[R = \frac{I_{R}}{I_{I}} = \frac{\frac{1}{2}\epsilon_{1}v_{1}E^2_{R,0}\cos \theta_{R}}{\frac{1}{2}\epsilon_{1}v_{1}E_{I,0}^2\cos \theta_{I}} = \left( \frac{\alpha-\beta}{\alpha+\beta} \right)^2\] \[T = \frac{I_{T}}{I_{I}} = \frac{\frac{1}{2}\epsilon_{2}v_{2}E_{T,0}^2\cos \theta_{T}}{\frac{1}{2}\epsilon_{1}v_{1}E_{I,0}^2\cos \theta_{I}} = \alpha\beta\left( \frac{2}{\alpha+\beta} \right)^2\]

공기/유리 경계면에 대해 R과 T를 \(\theta_{I}\)에 대한 함수로 그래프를 그린 것이 위와 같다. \(\theta_{I}=\theta_{B}\)인 경우 \(R=0\), \(T=1\)임을 확인할 수 있다.

(Case II) \(\vec{E}_{I}\)가 입사면과 수직한 경우

[!note] Boundry Condtiions{title}

\[\epsilon_{1}(\tilde{\vec{E}}_{I,0} + \tilde{\vec{E}}_{R,0})_{z} = \epsilon_{2}(\tilde{\vec{E}}_{T,0})_{z}\] \[(\tilde{\vec{B}}_{I,0} + \tilde{\vec{B}}_{R,0})_{z} = (\tilde{\vec{B}}_{T,0})_{z}\] \[(\tilde{\vec{E}}_{I,0} + \tilde{\vec{E}}_{R,0})_{x,y} = (\tilde{\vec{E}}_{T,0})_{x,y}\] \[\frac{1}{\mu_{1}}(\tilde{\vec{B}}_{I,0} + \tilde{\vec{B}}_{R,0})_{x,y} = \frac{1}{\mu_{2}} (\tilde{\vec{B}}_{T,0})_{x,y}\]

이는 \((\tilde{\vec{E}}_{I,0})_{x,z} = 0\), \((\tilde{\vec{B}}_{I,0})_{y} = 0\)인 경우와 같다. 이 경우, 세 파동의 자기장 벡터가 입사면 위에 존재하며, 편광 벡터는 y 성분만 존재한다.

[!question]- 왜 세 파동의 자기장 벡터가 입사면 위에 존재하며, 편광 벡터는 y 성분만 존재하는가?{title} 우선, 세번째 바운더리 컨디션으로 다음 조건을 얻는다.

\[(\tilde{\vec{E}}_{R,0})_{x} = (\tilde{\vec{E}}_{T,0})_{x}\]

이때, \(\tilde{\vec{E}}_{0}\)을 \(\tilde{\vec{B}}_{0}\)에 대해 쓰면 다음과 같다.

\[\tilde{\vec{B}}_{0} = \frac{1}{v} \hat{k} \times \tilde{\vec{E}}_{0}\] \[\implies \hat{k} \times (v\tilde{\vec{B}}_{0}) = \hat{k} \times (\hat{k} \times \tilde{\vec{E}_{0}})\]

벡터 삼중곱은 \(\vec{B}(\vec{A} \cdot \vec{C}) - \vec{C}(\vec{A} \cdot \vec{B})\)와 같다.

\[\hat{k} \times (\hat{k} \times \tilde{\vec{E}}_{0}) = \hat{k} (\hat{k} \cdot \tilde{\vec{E}}_{0}) - \tilde{\vec{E}}_{0} (\hat{k} \cdot \hat{k}) = - \tilde{\vec{E}}_{0}\] \[\therefore ~ \tilde{\vec{E}}_{0} = - \hat{k} \times (v\tilde{\vec{B}}_{0}) = v \tilde{\vec{B}}_{0} \times \hat{k}\]

따라서 다음과 같다.

\[(v_{1}\tilde{\vec{B}}_{R,0} \times \hat{k}_{R})_{x} = (v_{2}\tilde{\vec{B}}_{T,0} \times \hat{k}_{T})_{x}\] \[\implies (v_{1}\tilde{\vec{B}}_{R,0} \times (\sin \theta_{R} \hat{x} - \cos \theta_{R}\hat{z}))_{x} = (v_{2}\tilde{\vec{B}}_{T,0} \times (\sin \theta_{T} \hat{x} + \cos \theta_{T}\hat{z}))_{x}\]

외적해서 \(x\)성분이 나오려면, \(y,z\) 성분이 외적되어야 한다. \(\tilde{\vec{B}}_{0}\)은 모든 성분을 가지고 있다고 가정하면, \(B\)의 \(y\)성분만 남게 된다. \(\hat{y} \times \hat{z} =\hat{x}\)이므로 다음과 같다.

\[v_{1}(\tilde{\vec{B}}_{R,0})_{y} (-\cos \theta_{R}) \hat{x} = v_{2}(\tilde{\vec{B}}_{T,0})_{y}(\cos \theta_{T})\hat{x}\] \[\implies v_{1}\cos \theta_{R} (\tilde{\vec{B}}_{R,0})_{y} + v_{2} \cos \theta_{T} (\tilde{\vec{B}}_{T,0})_{y} = 0\]

네번째 바운더리 컨디션으로 다음 조건을 얻는다.

\[\frac{1}{\mu_{1}}(\tilde{\vec{B}}_{R,0})_{y} = \frac{1}{\mu_{2}}(\tilde{\vec{B}}_{T,0})_{y}\]

두 식을 연립하면, 다음과 같다.

\[v_{1}\cos \theta_{R} \frac{\mu_{1}}{\mu_{2}} (\tilde{\vec{B}}_{T,0})_{y} + v_{2}\cos \theta_{T}(\tilde{\vec{B}}_{T,0})_{y} = 0\] \[\implies (\tilde{\vec{B}}_{T,0})_{y} (v_{1}\mu_{1} \cos \theta_{R} + v_{2}\mu_{2}\cos \theta_{T}) = 0\]

위 항등식이 성립하려면, \(\tilde{\vec{B}}_{T,0}=0\)이거나, \(v_{1}\mu_{1}\cos \theta_{R} + v_{2}\mu_{2}\cos \theta_{T} =0\)이어야 한다. \(v_{1}\mu_{1}\)과 \(v_{2}\mu_{2}\)는 양수 값이므로, \(\cos \theta_{R}\) 또는 \(\cos \theta_{T}\)값 중 하나가 음수값이 되어야 한다. 그럴 수 없으므로, 항상 다음 조건을 만족해야 한다.

\[(\tilde{\vec{B}}_{T,0})_{y} = 0\]

네번째 바운더리 컨디션으로 얻은 조건을 통해 \((\tilde{\vec{B}}_{R,0})_{y}=0\) 또한 0임을 알 수 있다.

반사파, 투과파의 자기장의 \(y\)성분이 없다. 즉, 자기장 벡터는 입사면 내에 존재한다. 편광 벡터(전기장)은 \(xz\) 평면과 수직해야 하므로, \(y\)성분만 존재한다.

Boundry Condition을 사용해서 진폭 간의 관계를 유도하자. 목표는 \(\tilde{E}_{R,0}\)과 \(\tilde{E}_{T,0}\)을 \(\tilde{E}_{I,0}\)에 대한 식으로 쓰는 것이다.

첫번째 바운더리 컨디션은 다음과 같다.

\[\epsilon_{1}(\tilde{\vec{E}}_{I,0} + \tilde{\vec{E}}_{R,0})_{z} = \epsilon_{2}(\tilde{\vec{E}}_{T,0})_{z}\]

전기장의 \(z\) 성분이 없으므로, 의미 없다.

두번째 바운더리 컨디션은 다음과 같다.

\[(\tilde{\vec{B}}_{I,0} + \tilde{\vec{B}}_{R,0})_{z} = (\tilde{\vec{B}}_{T,0})_{z}\] \[-\tilde{B}_{I,0}\sin \theta_{I} - \tilde{B}_{R,0}\sin \theta_{R} = -\tilde{B}_{T,0}\sin \theta_{T}\]

이때, \(\tilde{\vec{B}}_{0} = \frac{1}{v} \hat{k} \times \tilde{\vec{E}}_{0}\)이므로, 좌변과 우변의 두 벡터의 크기가 같아야 한다. \(\tilde{B}_{0} = \frac{1}{v}\tilde{E}_{0}\) 관계를 사용한다.

\[\frac{1}{v_{1}} \tilde{E}_{I,0}\sin \theta_{I} + \frac{1}{v_{1}}\tilde{E}_{R,0}\sin \theta_{R} = \frac{1}{v_{2}}\tilde{\vec{E}}_{T,0}\sin \theta_{T}\] \[\implies \frac{\sin \theta_{I}}{v_{1}} (\tilde{E}_{I,0} + \tilde{E}_{R,0}) = \left( \frac{\sin \theta_{T}}{v_{2}} \right)\tilde{E}_{T,0}\] \[\implies \tilde{E}_{I,0} + \tilde{E}_{R,0} = \left( \frac{\sin \theta_{T}}{\sin \theta_{I}} \frac{v_{1}}{v_{2}} \right) \tilde{E}_{T,0}\] \[\implies \tilde{E}_{I,0} + \tilde{E}_{R,0} = \left( \frac{n_{1}}{n_{2}} \frac{n_{2}}{n_{1}} \right) \tilde{E}_{T,0} = \tilde{E}_{T,0}\]

세번째 바운더리 컨디션은 다음과 같다.

\[(\tilde{\vec{E}}_{I,0} + \tilde{\vec{E}}_{R,0})_{x,y} = (\tilde{\vec{E}}_{T,0})_{x,y}\] \[\implies (-\tilde{E}_{I,0}\hat{y} - \tilde{E}_{R,0}\hat{y})_{x,y} = (-\tilde{E}_{T,0})_{x,y}\] \[\implies \tilde{E}_{I,0} + \tilde{E}_{R,0} = \tilde{E}_{T,0}\]

이는 두번째 바운더리 컨디션과 같은 정보를 준다.

네번째 바운더리 컨디션은 다음과 같다.

\[\frac{1}{\mu_{1}}(\tilde{\vec{B}}_{I,0} + \tilde{\vec{B}}_{R,0})_{x,y} = \frac{1}{\mu_{2}}(\tilde{\vec{B}}_{T,0})_{x,y}\] \[\frac{1}{\mu_{1}}(\tilde{B}_{I,0}\cos \theta_{I} - \tilde{B}_{R,0} \cos \theta_{R}) = \frac{1}{\mu_{2}} (\tilde{B}_{T,0}\cos \theta_{T})\]

\(\theta_{I} = \theta_{R}\)와 \(\tilde{B}_{I,0} = \frac{1}{v}\tilde{E}_{0}\)을 적용한다.

\[\implies \frac{1}{\mu_{1}v_{1}}(\tilde{E}_{I,0}\cos \theta_{I} - \tilde{E}_{R,0}\cos \theta_{I}) = \frac{1}{\mu_{2}v_{2}} \tilde{E}_{T,0}\cos \theta_{T}\] \[\implies\tilde{E}_{I,0} - \tilde{E}_{R,0} = \left( \frac{\cos \theta_{T}}{\cos \theta_{I}} \frac{\mu_{1}v_{1}}{\mu_{2}v_{2}} \right) \tilde{E}_{T,0}\] \[\implies \tilde{E}_{I,0} - \tilde{E}_{R,0} = \alpha \beta \tilde{E}_{T,0}\]

두 식을 연립한다.

\[2\tilde{E}_{I,0} = (1+\alpha \beta)\tilde{E}_{T,0} \implies \tilde{E}_{T,0} =\left( \frac{2}{1+\alpha \beta} \right) \tilde{E}_{I,0}\] \[\tilde{E}_{I,0} + \tilde{E}_{R,0} = \left( \frac{2}{1+\alpha \beta} \right)\tilde{E}_{I,0} \implies \tilde{E}_{R,0} = \left( \frac{1-\alpha \beta}{1+\alpha \beta} \right)\tilde{E}_{I,0}\]

이것이 편광 벡터가 입사면과 수직할 때 프레넬 공식이다.

만약 \(\alpha = \beta^{-1}\)이 되면, 똑같이 반사파가 존재하지 않을까? 결론적으로 그렇지 않다. 편광 벡터가 입사면과 수직한 경우, 반사파가 반드시 존재한다.

[!question]- 왜 \(\alpha=\beta^{-1}\)을 만족하는 각이 존재하지 않는가?{title}

\[\alpha = \beta^{-1} \implies \frac{\cos \theta_{T}}{\cos \theta_{I}} = \frac{\sqrt{ 1-\sin^2\theta_{T} }}{\sqrt{ 1-\sin^2\theta_{I} }} = \frac{\sqrt{ 1- \left( \frac{n_{1}}{n_{2}} \right)^2\sin^2\theta_{I} }}{\sqrt{ 1-\sin^2\theta_{I} }} = \beta^{-1}\] \[\implies 1-\left( \frac{n_{1}}{n_{_{2}}} \right)^2\sin^2\theta_{I} = (1-\sin^2\theta_{I})\beta^{-2}\] \[\implies \sin^2\theta_{I}\left( \beta^{-2} - \left( \frac{n_{1}}{n_{2}} \right)^2 \right) = \beta^{-2} - 1\] \[\implies \sin^2\theta_{I} = \frac{1-\beta^{-2}}{\left( \frac{n_{1}}{n_{2}} \right)^2 - \beta^{-2}}\]

이때, \(\beta^{-2}\)는 다음과 같다.

\[\beta^{-2} = \left( \frac{\mu_{1}v_{1}}{\mu_{2}v_{2}} \right)^{-2} \simeq \left( \frac{v_{1}}{v_{2}} \right)^{-2} = \left( \frac{n_{1}}{n_{2}} \right)^2\]

따라서, 분모가 0이 되며, \(\alpha=\beta^{-1}\) 관계를 만족하는 입사각 \(\theta_{B}\)가 존재하지 않는다.