기초전자기학 22. 전자기 파동방정식의 해는 무엇일까
전자기 파동방정식의 해는 무엇인가?
전기장과 자기장은 파동이다. 정확하게는,
\[\frac{\partial^2 E_{i}}{\partial x_{i}^2} = \mu_{0}\epsilon_{0} \frac{\partial^2 E_{i}}{\partial t^2}\] \[\frac{\partial^2 B_{i}}{\partial x_{i}^2} = \mu_{0} \epsilon_{0} \frac{\partial^2B_{i}}{\partial t^2}\]전기장과 자기장 각각의 성분이 파동 방정식을 만족한다. 즉, 각각의 성분이 파동처럼 거동한다. 가장 심플한 케이스부터 살펴보자. 파동의 \(\omega\)이 변하지 않고 고정인 경우를 보자. \(\omega\)가 고정이면, \(\omega=2\pi f\)이므로 \(f\)가 고정이다. \(f\)가 고정이면, \(c= \lambda f\)이므로 \(\lambda\)가 고정이다. 이러한 파동을 단색(monochromatic) 파동이라고 한다. 단색 파동은 단일 파동이다.
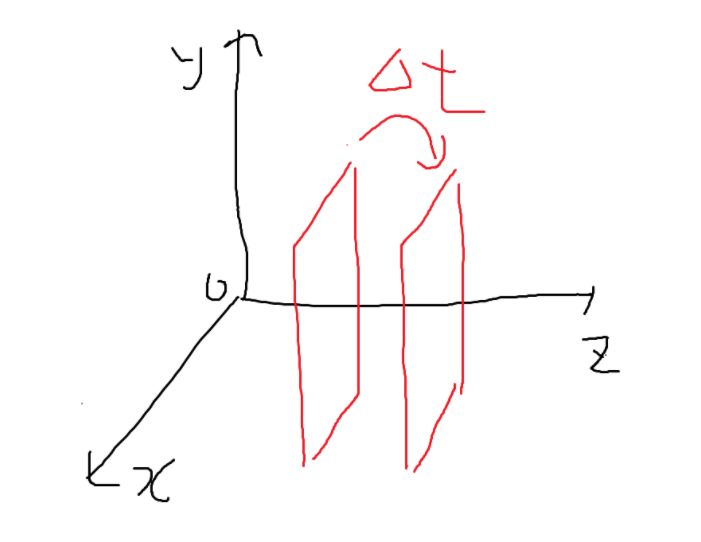
또한 파동이 \(z\) 방향으로만 변하고, \(x, y\) 방향의 변화는 없다고 가정한다. 이러한 파동을 Plane waves (평면파) 라고 한다.
그 이유는, 임의의 한 지점 \((z,t)\)에서의 전기장의 \(x, y\) 성분이 \((z+\Delta z, t+\Delta t)\) 이후 전기장의 \((x,y)\) 성분이 동일하기 때문이다. 전기장의 \(x, y\) 성분은 \(x,y\) 평면과 평행하고, 이를 파면으로 해석하면 z축 기준으로 파면이 점점 다가오거나 멀어지는 것 처럼 보이게 된다.
즉 단색 평면파의 해는 다음과 같다.
\[\tilde{E}_{i}(z,t) = \tilde{E}_{i, 0} e^{i(kz - \omega t)}\] \[\tilde{B}_{i}(z,t) = \tilde{B}_{i, 0} e^{i(kz - \omega t)}\]이 해는 맥스웰 방정식을 만족해야 한다. 파동방정식이 맥스웰 방정식에서 나왔고, 파동방정식의 해는 자동으로 맥스웰 방정식을 만족하는 것 아니냐? 그렇지 않다. 파동 방정식을 유도할 때, 맥스웰 방정식을 전부 사용한게 아니기 때문이다. 맥스웰 방정식의 해는 모두 파동방정식을 만족하지만, 그 역은 성립하지 않는다. 따라서 맥스웰 방정식을 Boundry Condition처럼 사용할 수 있다.
(1) \(\nabla \cdot \vec{E} = 0\)
\[\nabla \cdot \vec{E} = \frac{\partial}{\partial z} \tilde{E}_{z}(z,t) = \frac{\partial}{\partial z} \tilde{E}_{z,0}e^{i(kz-\omega t)}\] \[= \tilde{E}_{z,0} \cdot (ik) e^{i(kz-\omega t)} = 0 \implies \tilde{E}_{z,0} = 0\](2) \(\nabla \cdot \vec{B} = 0\)
\[\nabla \cdot \vec{B} = 0 \implies \tilde{B}_{z,0} = 0\]전기장과 자기장은 평면파이므로 \(x, y\) 성분의 변화는 0이다. 따라서 \(z\) 성분만 고려한다. 계산 결과, 전기장과 자기장의 \(z\) 성분이 존재하지 않는다. 즉, 전기장과 자기장은 전자기파의 진행 방향과 항상 수직이다.
(3) \(\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}\)
\[(\nabla \times \vec{E})_{x} = \sum_{j,k}\epsilon_{xjk} \partial_{j} \tilde{E}_{k}(z,t) = \epsilon_{xyz}\partial_{y}\tilde{E}_{z} + \epsilon_{xzy}\partial_{z} \tilde{E}_{y}\] \[= \partial_{y}\tilde{E}_{z} - \partial_{z}\tilde{E}_{y} \implies - \partial_{z}\tilde{E}_{y} = - \frac{\partial \tilde{B}_{x}}{\partial t}\] \[\implies \tilde{E}_{y,0}(ik)e^{i(kz-\omega t)} = \tilde{B}_{x,0}(-i\omega)e^{i(kz-\omega t)}\] \[\implies \tilde{B}_{x,0} = -\frac{k}{\omega} \tilde{E}_{y,0}\] \[(\nabla \times \vec{E})_{y} = \sum_{j,k}\epsilon_{yjk}\partial_{j}\tilde{E}_{k} = \epsilon_{yxz}\partial_{x}\tilde{E}_{z} + \epsilon_{yzx}\partial_{z}\tilde{E}_{x}\]\(\epsilon_{yxz} = \epsilon_{213} = -1\), \(\epsilon_{yzx} = \epsilon_{231} = 1\)과 같다.
\[= \partial_{z}\tilde{E}_{x} - \partial_{x}\tilde{E}_{z} \implies \partial_{z}\tilde{E}_{x} = - \frac{\partial \tilde{B}_{y}}{\partial t}\] \[\implies \tilde{E}_{x,0} (ik) e^{i(kz-\omega t)} = -\tilde{B}_{y,0}(-i\omega)e^{i(kz-\omega t)}\] \[\implies \tilde{B}_{y,0} = \frac{k}{\omega} \tilde{E}_{x,0}\] \[(\nabla \times \vec{E})_{z} = \sum_{j,k}\epsilon_{zjk} \partial_{j}\tilde{E}_{k} = \epsilon_{zxy}\partial_{x}\tilde{E}_{y} + \epsilon_{zyx} \partial_{y}\tilde{E}_{z}\] \[= \partial_{x}\tilde{E}_{y} - \partial_{y}\tilde{E}_{z} = - \frac{\partial \tilde{B}_{z}}{\partial t}\]\(\tilde{B}_{z} = \tilde{E}_{z} = 0\)이고, \(\tilde{E}_{y}\)를 \(x\)에 대해 미분하면, \(x\)항은 없으므로 0이다. 따라서 의미 없다.
\[\tilde{B}_{x,0} = - \frac{k}{\omega}\tilde{E}_{y,0}, ~~\tilde{B}_{y,0} = \frac{k}{\omega}\tilde{E}_{x,0}\]이를 한큐에 표현하면 다음과 같다.
\[\tilde{\vec{B}}_{0} = \frac{k}{\omega} (\hat{z} \times \tilde{\vec{E}}_{0})\][!question]- Why?{title} (1) \(\tilde{B}_{x,0}\)
\[\tilde{B}_{x,0} = \frac{k}{\omega}(\hat{z} \times \tilde{\vec{E}}_{0})_{x}\] \[= \frac{k}{\omega} \sum_{j,k}\epsilon_{xjk}z_{j}\tilde{E}_{k,0} = \frac{k}{\omega}(\epsilon_{xyz} z_{y}\tilde{E}_{z,0} + \epsilon_{xzy}z_{z}\tilde{E}_{y,0})\] \[= -\frac{k}{\omega} \tilde{E}_{y,0}\](2) \(\tilde{B}_{y,0}\)
\[\tilde{B}_{y,0} = \frac{k}{\omega}(\hat{z} \times \tilde{\vec{E}}_{0})_{y}\] \[= \frac{k}{\omega}\sum_{j,k}\epsilon_{yjk}z_{j}\tilde{E}_{k,0} = \frac{k}{\omega} (\epsilon_{yxz}z_{x}\tilde{E}_{z,0} + \epsilon_{yzx}z_{z}\tilde{E}_{x,0})\] \[= \frac{k}{\omega}\tilde{E}_{x,0}\]
이 결과를 통해 무엇을 알 수 있는가? (1)에서 전기장은 진행방향 \(\hat{z}\)과 수직하다는 결과를 얻었다. \(\hat{z}\)과 전기장을 외적한 결과가 자기장이라는 것은, \(\hat{z}\)과 전기장이 이루는 평면과 자기장은 항상 수직하다는 것과 같다. 즉, 전기장, 자기장, 진행방향은 모두 직교한다는 결론을 얻는다.
\(\vec{E} \times \vec{B}\)는 전자기파의 진행 방향과 같다. \(\vec{E} \times \vec{B}\)는 무엇인가? 포인팅 벡터와 같다. 즉 에너지의 흐름과 전자기파의 진행 방향이 동일하다는 것은 자연스러운 결과다.
또, \(\omega = v \lvert k \rvert\)이므로 \(\omega = ck \implies \frac{k}{\omega} = \frac{1}{c}\)와 같다. 자기장은 전기장보다 \(\frac{1}{c}\)만큼 작다. 자기장의 세기는 전기장보다 상대적으로 많이 작다는 사실도 알 수 있다.
\[B_{0} = \frac{1}{c}E_{0}\](4) \(\nabla \times \vec{B} = \mu_{0}\epsilon_{0} \frac{\partial \vec{E}}{\partial t}\) 새로운 결과를 만들어내지 못하고, (3) 과 동일한 결과를 얻는다.
위 결과를 통해 일반해를 분석해보자.
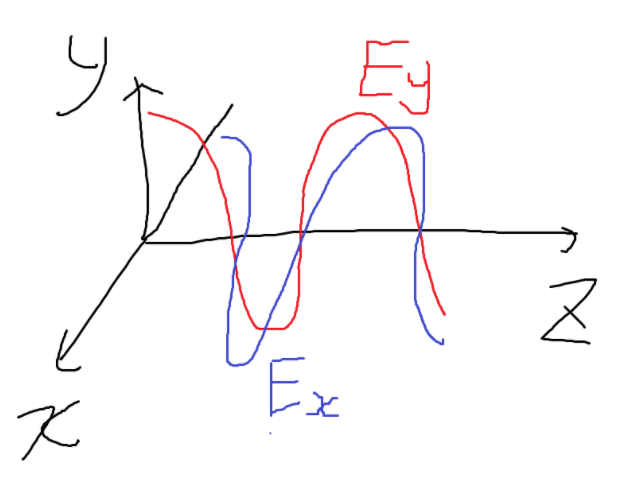
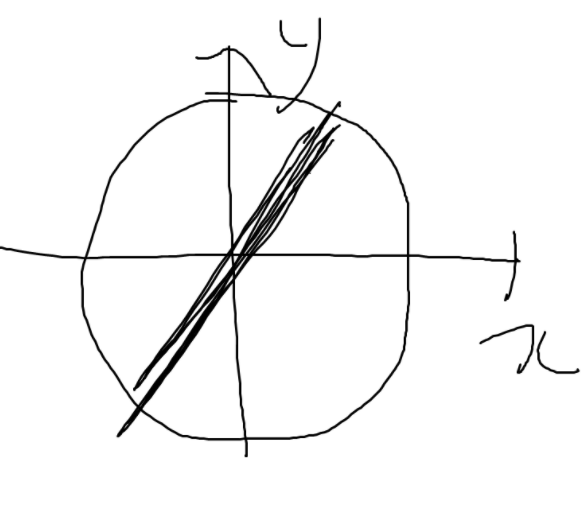
\[\tilde{\vec{E}}(z,t) = \tilde{\vec{E}}_{0}e^{i(kz - \omega t)}\] \[= (\tilde{E}_{x,0}\hat{x} + \tilde{E}_{y,0}\hat{y}) e^{i(kz-\omega t)}\] \[= (E_{x,0}e^{i \delta_{x}}\hat{x} + E_{y,0}e^{i\delta_{y}} \hat{y}) e^{i(kz-\omega t)}\] \[\implies \vec{E}(z,t) = \mathrm{Re}[\tilde{\vec{E}}(z,t)] = (E_{x,0}\cos(kz-\omega t + \delta_{x}))\hat{x} + (E_{y,0}\cos(kz-\omega t + \delta_{y}))\hat{y}\]만약 \(\delta_{x} = \delta_{y}\)인 경우, 위상이 같으므로 x축과 y축의 파동이 똑같이 움직인다.
이 전기장을 \(z\)축 에서 바라보면 다음과 같이 한쪽 방향으로 왔다갔다하는 모양으로 보인다.
빛을 편광하는 아이디어가 여기서 나온다. 특정 각도의 틈을 만들고 빛을 쐬어주면, 특정 각도로 왔다갔다하는 빛만 투과된다. 일정한 방향의 빛만 골라낼 수 있다!
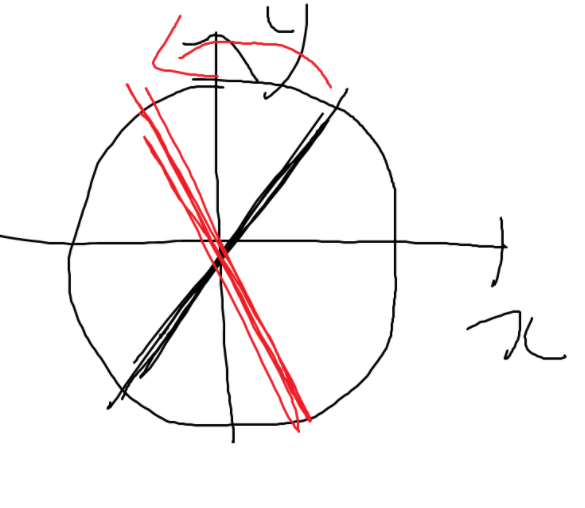
만약 \(\delta_{x} \neq \delta_{y}\)의 경우 복잡해진다. \(x, y\) 파동이 서로 다른 위상을 가지고 있으므로, 특정 각도로 왔다갔다 하는게 아니라 뱅글뱅글 도는 모양이 된다.
그 모양은 일반적으로 타원 모양이다. 위상이 같은 경우가 Speacial case고, 많은 빛은 일반적으로 위와 같이 거동한다.
전기장과 자기장을 동시에 분석해보자. 전기장과 자기장은 각각 \(\hat{x}, \hat{y}\) 성분이 있지만, 한쪽 성분만 분석해보자. 한쪽 성분만 봐도 나머지 성분은 똑같이 거동한다.
\[\tilde{\vec{E}}(z,t) = \tilde{E}_{x,0}e^{i(kz-\omega t)}\hat{x}, ~~\tilde{\vec{B}}(z,t) = \tilde{B}_{y,0}e^{i(kz-\omega t)}\hat{y}\]전기장이 \(\hat{x}\) 성분이면 자기장은 \(\hat{y}\) 성분과 대응된다. 실수부를 취한다.
\[\vec{E}(z,t) = E_{0}\cos(kz-\omega t- \delta) \hat{x}, ~~\vec{B}(z,t) = B_{0} \cos(kz-\omega t-\delta) \hat{y}\]위상은 동일하다고 가정한다.
전자기파는 위와 같은 모양으로 진행한다. 진폭은 \(B_{0} = \frac{E_{0}}{c}\) 관계에 있다.
일반적인 방향의 전자기파는?
\(\vec{k}\) 방향으로 진행하는 전자기파는 다음과 같다.
\[\tilde{\vec{E}}(\vec{r}, t) = \tilde{E}_{0} e^{i(\vec{k} \cdot \vec{r} - \omega t)}\hat{n}\] \[\tilde{\vec{B}}(\vec{r},t) = \frac{1}{c} \tilde{E}_{0} e^{i(\vec{k} \cdot \vec{r} - \omega t)}(\hat{k} \times \hat{n})=\frac{1}{c}\hat{k} \times \tilde{\vec{E}}(\vec{r},t)\]이때 \(\hat{n}\)은 \(\hat{n} \cdot \vec{k} = 0\)을 만족하는 단위 벡터다.
전자기파의 에너지, 운동량 밀도는?
전자기장에 저장된 에너지 밀도는 다음과 같다.
\[u = \frac{\epsilon_{0}}{2}E^2 + \frac{1}{2\mu_{0}} B^2\]단색 평면파에서 전기장과 자기장 관계는 다음과 같다.
\[\tilde{\vec{B}} = \frac{1}{c} \hat{k} \times \tilde{\vec{E}}\] \[\lvert B \rvert ^2 = \tilde{\vec{B}}^* \cdot \tilde{\vec{B}} = \frac{1}{c^2} (\hat{k} \times \tilde{\vec{E}}^*) \cdot (\hat{k} \times \tilde{\vec{E}})\]Consider. \((\vec{A} \times \vec{B}) \cdot (\vec{C} \times \vec{D})\)
\[(\vec{A} \times \vec{B}) \cdot (\vec{C} \times \vec{D}) = \sum_{i}(\vec{A} \times \vec{B})_{i}(\vec{C} \times \vec{D})_{i}\] \[= \sum_{i}\left( \sum_{j,k} \epsilon_{ijk} A_{j}B_{k} \right)\left( \sum_{l,m} \epsilon_{ilm} C_{l}D_{m} \right)\] \[= \sum_{i,j,k,l,m}\epsilon_{ijk} \epsilon_{ilm} A_{j}B_{k}C_{l}D_{m}\] \[= \sum_{j,k,l,m}(\delta_{jl}\delta_{km} - \delta_{jm}\delta_{kl})(A_{j}B_{k}C_{l}D_{m})\] \[= \sum_{j,k}(A_{j}B_{k}C_{j}D_{k} - A_{j}B_{k}C_{k}D_{j})\] \[= \sum_{j}A_{j}C_{j} \sum_{k}B_{k}D_{k} - \sum_{j} A_{j} D_{j} \sum_{k}B_{k}C_{k}\] \[= (\vec{A} \cdot \vec{C})(\vec{B} \cdot \vec{D}) - (\vec{A} \cdot \vec{D})(\vec{B} \cdot \vec{C})\]따라서 다음과 같다.
\[\lvert \vec{B} \rvert^2 = \frac{1}{c^2}((\hat{k} \cdot \hat{k})(\tilde{\vec{E}}^* \cdot \tilde{\vec{E}}) - (\hat{k} \cdot \tilde{\vec{E}})(\tilde{\vec{E}}^* \cdot \hat{k}))\]\(\vec{k}\)와 \(\tilde{\vec{E}}\)는 수직이므로, 내적 결과가 0이다.
\[= \frac{1}{c^2} \lvert E \rvert^2 = \mu_{0}\epsilon_{0} \lvert E \rvert^2\]따라서 다음과 같다.
\[u = \frac{\epsilon_{0}}{2}E^2 + \frac{1}{2\mu_{0}} \mu_{0}\epsilon_{0}E^2 = \frac{\epsilon_{0}}{2}E^2 + \frac{\epsilon_{0}}{2}E^2 = \epsilon_{0}E^2\] \[= \epsilon_{0} \left( \frac{1}{\mu_{0}\epsilon_{0}}B^2 \right) = \frac{1}{\mu_{0}}B^2\] \[\therefore ~~ u = \epsilon_{0}E^2 = \frac{1}{\mu_{0}}B^2\]전기장과 자기장은 에너지를 각각 절반씩 나눠 가지고 있다. 따라서 전기장 또는 자기장의 에너지에 2배한 값은 단색 평면파가 갖는 총 에너지와 같다.
이 에너지의 흐름은 포인팅 벡터의 방향과 같다.
\[\vec{S} = \frac{1}{\mu_{0}}(\vec{E} \times \vec{B})\]\(\vec{E}\)와 \(\vec{B}\)는 각각 \(\tilde{\vec{E}}, \tilde{\vec{B}}\)에서 Real을 취한 것과 같다.
\[\vec{E} = \mathrm{Re}[\tilde{\vec{E}}_{0}e^{i(\vec{k} \cdot \vec{r} - \omega t)}] = E_{0}\cos(\vec{k} \cdot \vec{r} - \omega t + \delta)\hat{n}\] \[\vec{B} = \mathrm{Re}[\tilde{\vec{B}}_{0}e^{i(\vec{k} \cdot \vec{r} - \omega t)}] = B_{0}\cos(\vec{k} \cdot \vec{r} - \omega t + \delta) = \frac{1}{c}E_{0}\cos(\vec{k} \cdot \vec{r} - \omega t + \delta)(\hat{k} \times \hat{n})\]따라서 다음과 같다.
\[\vec{S} = \frac{1}{\mu_{0}} \frac{1}{c} E_{0}^2 \cos^2(\vec{k} \cdot \vec{r} - \omega t + \delta) (\hat{n} \times (\hat{k} \times \hat{n}))\] \[= \frac{\sqrt{ \mu_{0}\epsilon_{0} }}{\mu_{0}} E_{0}^2 \cos^2(\vec{k} \cdot \vec{r} - \omega t + \delta) \hat{k}\] \[= \epsilon_{0}cE_{0}^2 \cos^2(\vec{k} \cdot \vec{r} - \omega t + \delta)\hat{k}\]\(E_{0}^2\cos^2(\vec{k} \cdot \vec{r} - \omega t + \delta) = E^2\)와 같고, \(\epsilon_{0}E^2 = u\)와 같다.
\[= cu\hat{k}\]이는 당연한 결과다! \(\vec{S}\)는 단위 면적, 단위 시간동안 에너지 변화와 같다. 에너지 밀도 \(u\)는 단위 부피당 에너지와 같다. 단위 시간 \(\Delta t\)동안 단위면적 \(\Delta A\)를 지나가는 단위 부피 내의 에너지는 \((c\Delta t \Delta A) u\)와 같다. 따라서 단위 면적, 단위 시간동안 에너지는 \(cu\)와 같다.
전자기파는 운동량도 가지고있다.
\[\vec{g} = \mu_{0}\epsilon_{0}\vec{S} = \frac{1}{c^2}\vec{S} = \frac{u}{c}\hat{k}\]따라서 \(\vec{S} = cu\hat{k}\), \(\vec{g} = \frac{u}{c}\hat{k}\)와 같고, \(u= \epsilon_{0}E^2(\vec{r}, t)\)이므로 \(\vec{S}\), \(\vec{g}\)는 위치, 시간에 대한 함수와 같다.
[!question] 에너지 밀도가 시간과 위치에 대한 함수라고? 그럼 에너지 보존 법칙 위반 아니야?{title} 진공에서의 전자기파가 있고 계가 보존계면 에너지는 항상 같아야 하는거 아닌가? 진공에서의 에너지에 대한 보존 법칙은 연속 방정식으로 기술된다.
\[\frac{\partial u}{\partial t} + \nabla \cdot \vec{S} = 0\]에너지 밀도 뿐만 아니라, 전자기파로 퍼져나가거나 들어오는 에너지까지 포함하여 에너지가 보존된다. 즉, 진공에서 에너지 밀도가 증가하면 전자기파를 통해 흘러 들어온 에너지 \(\nabla \cdot \vec{S} <0\)가 존재한 것이고, 에너지 밀도가 감소하면 전자기파로 에너지가 빠져나간 것 \(\nabla \cdot \vec{S} > 0\)이다.
각각의 물리량을 대충 평균내면 얼마일까? 즉, 대충 이정도 값이겠지~ 싶은 기대값이 얼마일까?
\[\langle u \rangle, \langle \vec{S} \rangle, \langle \vec{g} \rangle\] \[u = \epsilon_{0}E^2 = \epsilon_{0}E_{0}^2 \cos^2(\vec{k} \cdot \vec{r} - \omega t + \delta)\]\(\epsilon_{0}E^2_{0}\)은 상수이므로, 코사인을 평균내면 된다. 코사인은 \(\frac{2\pi}{\omega}\)만큼 주기를 갖는 주기함수이므로, 한 주기만 평균내도 무방하다.
\[\langle \cos^2(\vec{k} \cdot \vec{r} - \omega t + \delta) \rangle = \frac{w}{2\pi} \int_{0}^{2\pi/\omega} \cos^2(\vec{k} \cdot \vec{r} - \omega t + \delta)dt\] \[= \frac{\omega}{2\pi} \int_{0}^{2\pi/\omega} \frac{1}{2}(1+\cos(2(\vec{k} \cdot \vec{r} - \omega t + \delta)))dt\] \[= \frac{w}{2\pi} \frac{1}{2} \left[ t - \frac{1}{2\omega}\sin(2(\vec{k} \cdot \vec{r} - \omega t + \delta)) \right]^{2\pi/\omega}_{0}\] \[= \frac{1}{2} \frac{\omega}{2\pi} \left( \frac{2\pi}{\omega} \right) = \frac{1}{2}\]따라서 평균은 각 값의 절반이다. 평균 기호는 선형성이 있고, 상수 계수를 밖으로 뺄 수 있음.
전자기파의 세기(Intensity) 는 평균 포인팅 벡터의 크기로 정의한다.
\[I \equiv \lvert \langle \vec{S} \rangle \rvert = \frac{1}{2}c \epsilon_{0}E_{0}^2\]세기의 단위는 에너지 / (면적 \(\cdot\) 시간)이다. 이는 (일률 / 면적)과 같다.
또, 전자기파가 가하는 압력도 정의할 수 있다. 운동량의 변화량은 \(\Delta \vec{p} = \langle \vec{g} \rangle dV = \langle \vec{g} \rangle c\Delta t \Delta A\)와 같다. 운동량의 시간 변화는 힘과 같고, 단위 면적당 힘은 압력과 같다. 따라서 전자기파가 가하는 방사 압력 (radiantion pressure) 을 다음과 같이 정의한다.
\[P \equiv \frac{\Delta p}{\Delta t} \frac{1}{\Delta A} = \langle \vec{g} \rangle c = \frac{1}{2}\epsilon_{0}\vec{E}_{0}^2 = \frac{I}{c}\]방사 압력이란 단위 면적이 평균적으로 받는 힘의 크기와 같다. Photon의 질량은 0인데, 어떻게 압력을 만드는가? 전자기파가 만드는 압력은 질량에서 오지 않는다. 모든 입자는 미시적으로 전자 양성자에 의해 전하를 띈다. 전자기파의 전기장은 전하를 전기장 방향으로 움직이게 하고, 움직이는 전하는 전자기파의 자기장에 의해 \(q(\vec{v} \times \vec{B})\)만큼 힘을 받는다. 단위 면적이 받는 알짜힘의 총 합이 압력과 같다.
모든 전자기파는 평면파인가?
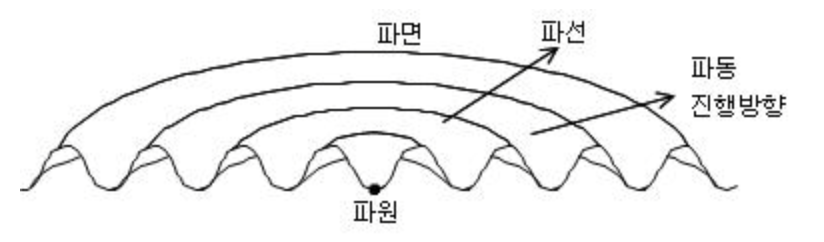
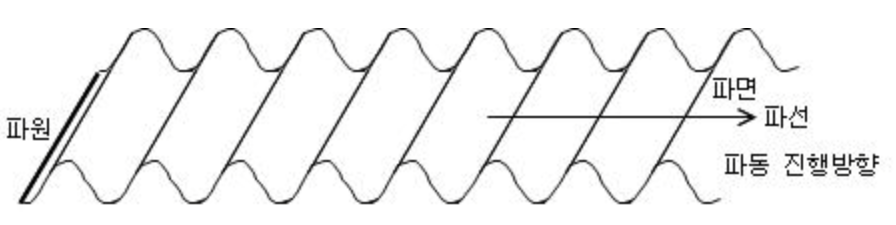
파동의 Source를 파원이라고 한다. 파원이 점이면 파동은 사방으로 퍼지고, 파원이 선이면 파동은 양쪽으로 퍼져나간다. 전자를 구면파, 후자를 평면파라고 부른다.
전자기파도 구면파가 있을 수 있고, 평면파가 있을 수 있다. 구면파가 아주 멀리 퍼져나가면, 평면파로 근사된다. 구면파에서 파원 근처에 있더라도, 좁은 영역이나 특정 방향만 보면 파면이 평면인 평면파로 볼 수도 있다.
.jpg)