기초전자기학 20. 파동방정식을 어떻게 풀까
파동 방정식을 어떻게 푸는가?
\[\frac{\partial^2f(z,t)}{\partial z^2} = \frac{1}{v^2} \frac{\partial^2f(z,t)}{\partial t^2}\]1차원 파동방정식을 풀어보자. 선형 동차 편미분방정식을 풀 때 가장 강력한 도구는 변수분리 방법이다. 따라서 다음과 같은 과감한 가정을 해보자.
\[f(z,t) = Z(z) U(t)\]따라서 다음과 같다.
\[Z''U = \frac{1}{v^2} ZU''\] \[\implies v^2\frac{Z''}{Z} = \frac{U''}{U} = \alpha\]좌변 우변이 각각 다른 변수로 분리된다. 두 독립변수가 항상 같으려면, 두 값이 상수어야 한다.
\[\frac{d^2U(t)}{dt^2} = \alpha U(t)\]만약 \(\alpha>0\)이면, 해는 \(U(t) = Ae^{\sqrt{ \alpha }t} + Be^{-\sqrt{ \alpha }t}\)로 쓸 수 있다. \(\alpha<0\)이면, 제곱해서 음수가 나온것과 같으므로 허수 항이 붙는다. 해는 \(U(t) = Ae^{i \sqrt{ \alpha }t} + Be^{-i \sqrt{ \alpha }t}\)와 같다. \(\alpha = 0\)이면, \(\frac{d^2U(t)}{dt^2} = 0 \implies U(t) = At+b\)와 같다.
\(\alpha\geq0\)의 경우, 지수함수 꼴이거나 선형 다항함수 꼴이다. 시간이 지나면 진폭이 무한이 커지고, 에너지가 무한히 커진다. 이는 물리적으로 맞지 않는 Soultion이다. 따라서, \(\alpha<0\) 해만 취하자. \(\alpha = -\omega^2\), \(\omega>0\)으로 정의한다.
\[U(t) = Ae^{i \omega t} + Be^{-i \omega t}\]이제 \(Z\)를 구해보자.
\[\frac{d^2Z(z)}{dz^2} = -\frac{\omega^2}{v^2} Z\]이때 \(k\)를 다음과 같이 정의한다. \(\omega>0\)임을 유의하라.
\[k^2 \equiv \frac{\omega^2}{v^2} \implies \omega^2 = v^2k^2 \implies \omega(k) = v \lvert k \rvert\]따라서 다음과 같다.
\[\frac{d^2Z(z)}{dz^2} = - k^2 Z \implies Z(z) = Fe^{ikz} + Ge^{-ikz}\]\(f(z,t)\)의 해는 무엇인가? \(f(z,t)\)는 복소 파동함수 \(\tilde{f}(z,t)\)를 구한 후 Real Part를 취하면 얻을 수 있다. 따라서 복소 파동함수 \(\tilde{f}(z,t)\)로 표현하기 위해, 모든 상수에 위상 상수를 포함하자.
\[\tilde{A} = Ae^{i \delta}, \dots\]즉, \(\tilde{f}(z,t)\)의 해는 다음과 같다.
\[\tilde{f}(z,t) = (\tilde{A}e^{iwt} + \tilde{B}e^{-i\omega t})(\tilde{F}e^{ikz} + \tilde{G}e^{-ikz})\] \[= \tilde{A}'e^{i(kz - \omega t)} + \tilde{B}'e^{-i(kz - \omega t)} + \tilde{F}'e^{i(kz + \omega t)} + \tilde{G}'e^{-i(kz + \omega t)}\]앞의 두 항은 오른쪽으로 가는 파동, 뒤의 두 항이 왼쪽으로 가는 파동을 의미한다. 위 Solution에서 \(k\)를 모든 범위에 대해 적분하면 General Solution을 얻을 수 있다.
여기서 잠시 왼쪽으로 가는 두 파동을 생각해보자.
\[\tilde{A}'e^{i(kz - \omega t)} + \tilde{B}'e^{-i(kz - \omega t)}\]두 복소 파동함수는 엄연히 다르다. \(\tilde{A}' = A'e^{i \delta}\), \(\tilde{B}'=B'e^{i\phi}\)로 설정하면 다음과 같다.
\[\tilde{A'}e^{i(kz-\omega t)} = A'e^{i \delta}e^{i kz - \omega t} = A'e^{i(kz - \omega t + \delta)}\] \[= A'(\cos (kz - \omega t + \delta) + i\sin(kz - \omega t + \delta))\] \[\tilde{B}'e^{-i(kz-\omega t)} = B'e^{-i(kz-\omega t-\phi)}\] \[= B'(\cos(kz - \omega t-\phi) - i\sin(kz - \omega t-\phi))\]위 두 함수는 같지 않다. 하지만 모든 \(k\)에 대해 적분한다면 이야기가 다르다. 첫번째 기저 \(e^{i(kz-\omega t)}\)는 푸리에 정리에 의해 오른쪽으로 가는 모든 파동함수를 표현할 수 있다. 두번째 기저 \(e^{-i(kz-\omega t)}\) 또한 오른쪽으로 가는 모든 파동함수를 표현할 수 있다. Span했을 때 두 기저가 표현하는 공간이 동일하므로, 두 기저는 종속 관계에 있다. General Solution를 쓸 땐 종속 관계에 있는 두 기저를 선형 결합할 필요가 없다. 따라서 하나를 생략해도 무방하다. 이 논리는 왼쪽으로 가는 파동도 동일하게 적용할 수 있다. 따라서 General Solution을 다음과 같이 간단하게 쓸 수 있다.
\[\tilde{f}(z,t) = \int_{-\infty}^{\infty}\tilde{C}_{right}(k)e^{i(kz-\omega t)}dk + \int_{-\infty}^{\infty} \tilde{C}_{left}(k)e^{i(kz+\omega t)}dk\]위 결과는 파동 방정식의 가장 일반적인 Solution인 달랑베르(d’Alembert)의 해와 동일하다.
\[f(z,t) = g(z-vt) + h(z+vt)\][!question] 푸리에 정리가 무엇인가?{title} \(L^1\) 또는 \(L^2\) 공간의 모든 함수는 \(e^{ikx}\)
\[f(x) = \frac{1}{\sqrt{ 2\pi }}\int_{-\infty}^{\infty} A(k)e^{ikx}dk\](사인파와 코사인파)를 잘 더하고 빼면 만들어낼 수 있다. 이것이 푸리에 정리다.\(x=z-vt\)를 대입하면 오른쪽으로 가는 파동함수가 만들어진다.
\[f(z-vt) = \frac{1}{\sqrt{ 2\pi }} \int_{-\infty}^{\infty}A(k)e^{ik(z-vt)}dk\]즉, 실수 함수 공간의 기저 \(e^{ik(z-vt)}\)는 오른쪽으로 가는 모든 파동을 만들어낼 수 있다.
(= 실수 함수 공간을 Span함)
[!question] 왜 \(e^{-i(kz-\omega t)}\)도 오른쪽으로 가는 모든 함수를 만들어 내는가?{title} 푸리에 변환 공식을 다음과 같이 적어보자.
\[f(x) = \mathrm{Re}\left[ \frac{1}{\sqrt{ 2\pi }} \int_{-\infty}^{\infty}\tilde{A}(k)e^{ikx}dk \right]\]\(f(x)\)는 Real 함수이므로, 복소켤레 \(*\)를 취해도 값이 같다.
\[f(x)^* = f(x) = \mathrm{Re}\left[ \frac{1}{\sqrt{ 2\pi }} \int_{-\infty}^{\infty}\tilde{A}(k)e^{ikx}dk \right]^*\] \[= \mathrm{Re}\left[ \frac{1}{\sqrt{ 2\pi }} \int_{-\infty}^{\infty}\tilde{A}(k)^*e^{-ikx}dk \right]\]\(x=z-vt\)를 대입하면, \(e^{-ik(z-vt)}\) 또한 실수 함수 공간 내의 오른쪽으로 가는 모든 파동을 만들어냄을 알 수 있다.
[!question] 달랑베르(d’Alembert)의 해가 무엇인가?{title} \(g(z-vt)\)는 파동방정식을 만족한다.
\[g''(z-vt) = \frac{\partial^2 g(z-vt)}{\partial z^2}\] \[\frac{\partial g(z-vt)}{\partial t} = -v g'(z-vt)\] \[\implies \frac{\partial^2g(z-vt)}{\partial t^2} = v^2 g''(z-vt)\] \[\therefore ~~ \frac{\partial^2 g(z-vt)}{\partial z^2} = \frac{1}{v^2} \frac{\partial^2 g(z-vt)}{\partial t^2}\]같은 논리로, \(h(z+vt)\) 또한 파동방정식을 만족한다. 두 해를 선형 결합한 결과도 파동 방정식을 만족한다. 따라서 일반적인 파동 방정식의 해는 다음과 같이 쓸 수 있다.
\[f(z,t) = g(z-vt) + h(z+vt)\]이것이 무엇을 의미하는가? 어떤 임의의 함수에 변수 대신 \(z\pm vt\)를 대입하면 파동 방정식을 만족하고, 따라서 파동 함수가 된다는 것을 의미한다.
위 일반해에서 Real Part만 취하면 \(f(z,t)\)를 구할 수 있다. 두 항을 쓰기 번거로운데, 아래와 같이 하나의 식으로 표현할 수 있을까?
\[f(z,t) = \mathrm{Re}\left[ \int_{-\infty}^{\infty}\tilde{C}(k)e^{i(kz-\omega t)}dk \right]\]위 식이 성립하려면, \(k\geq0\)일 때 아래 식
\[\int_{0}^{\infty}\tilde{C}(k)e^{i(kz-\omega t)}dk\]이 오른쪽으로 이동하는 모든 실수 파동 함수를 표현할 수 있어야 하고, \(k<0\)일 때 아래 식
\[\int_{-\infty}^{0}\tilde{C}(k)e^{i(kz+\omega t)}dk\]이 왼쪽으로 이동하는 모든 실수 파동 함수를 표현할 수 있어야 한다. 이것을 증명해보자.
[!question] 적분 범위의 절반만 사용해도, 복소 함수를 계수로 사용하면 모든 실수 함수를 표현할 수 있을까?{title}
\[f(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \tilde{A}(k)e^{ikx}dk\]이때 \(\tilde{A}(k)\)는 다음과 같다.
\[\tilde{A}(k) = \int_{-\infty}^{\infty} f(x')e^{-ikx'}dx'\]\(k>0\), \(k<0\)으로 두 적분으로 쪼개보자.
\[f(x) = \frac{1}{2\pi}\left[ \int_{0}^{\infty} \tilde{A}(k)e^{ikx}dk + \int_{-\infty}^{0}\tilde{A}(k)e^{ikx}dk \right]\]두번째 적분에 \(k\) 대신 \(-k\)를 대입해도 적분 값은 동일하다.
\[\int_{-\infty}^{0}\tilde{A}(k)e^{ikx}dk = \int_{\infty}^{0}\tilde{A}(-k)e^{-ikx}(-dk)\] \[= \int_{0}^{\infty} \tilde{A}(-k)e^{-ikx}dk\]이때, \(\tilde{A}(-k)\)는 다음과 같다.
\[\tilde{A}(-k) = \int_{-\infty}^{\infty} f(x')e^{-ikx'}dx'\]함수 \(f(x')\)는 실수 함수이므로, 아래와 같다.
\[\tilde{A}^*(k) = \int_{-\infty}^{\infty}f(x')e^{-ikx'}dx'\] \[\therefore ~~ \tilde{A}(-k) = \tilde{A}^*(k)\]따라서 다음과 같다.
\[f(x) = \frac{1}{2\pi} \left[ \int_{0}^{\infty} \tilde{A}(k)e^{ikx}dk + \int_{0}^{\infty}\tilde{A}^*(k)e^{-ikx}dk \right]\] \[f(x) = \frac{1}{2\pi} \left[ \int_{0}^{\infty} (\tilde{A}(k)e^{ikx} + \tilde{A}^*(k)e^{-ikx})dk \right]\]\(Z + Z^* = 2\mathrm{Re}[Z]\) 성질을 이용한다.
\[= \frac{1}{2\pi} \left[ \int_{0}^{\infty} 2\mathrm{Re}[\tilde{A}(k)e^{ikx}] dk\right]\] \[= \frac{1}{\pi} \mathrm{Re}\left[ \int_{0}^{\infty} \tilde{A}(k)e^{ikx}dk \right]\]따라서 기저가 \(e^{ikx}\)어도 계수가 복소 함수라면, \(k\)를 절반의 범위만 사용해도 실수 함수 \(f(x)\)정도는 모두 표현 가능함을 밝혔다.
결론적으로, 실수 파동 함수의 General Solution을 다음과 같이 표현할 수 있다.
\[f(z,t) = \mathrm{Re}\left[ \int_{-\infty}^{\infty}\tilde{C}(k)e^{i(kz-\omega t)}dk \right]\]1차원 파동 방정식을 어떻게 풀까? (Version 2)
변수분리 후 \(f(z,t)\) 를 찾아내는 과정까진 동일하다. 다음과 같이 쓸 수 있다.
\[\tilde{f}(z,t) = \tilde{D}(k,\omega)e^{i(\pm kz \pm \omega t)}\]실수 해를 취하면 다음과 같다.
\[f(z,t) = \mathrm{Re}[\tilde{D}(k,\omega)e^{i(\pm kz\pm \omega t)}]= \begin{cases} D(k,\omega) \cos(kz + \omega t) \\ D(k,\omega)\cos(kz - \omega t) \\ D(k,\omega) \cos(-kz + \omega t) \\ D(k,\omega) \cos(-kz - \omega t) \end{cases}\]이때 \(\cos(kz+\omega t) = \cos(-kz-\omega t)\), \(\cos(kz-\omega t) = \cos(-kz+\omega t)\)이므로 항을 줄일 수 있다.
\[f(z,t)=\mathrm{Re}[\tilde{A}e^{i(kz-\omega t)} + \tilde{B}e^{i(kz+\omega t)}]\]위 식을 모든 \(k\) 범위에 대해 적분하면 General Solution을 얻을 수 있다. \(\omega = v \lvert k \rvert\)이므로, 먼저 \(k>0\)에 대해 적분해보자.
\[f(z,t) = \mathrm{Re}\left[ \int_{0}^{\infty}\tilde{A}e^{i(kz-\omega t)}dk + \int_{0}^{\infty}\tilde{B}e^{i(kz+\omega t)}dk \right]\]두번째 항에 \(k\) 대신 \(-k\)를 대입해도 적분 결과는 같다.
\[= \mathrm{Re}\left[ \int_{0}^{\infty}\tilde{A}(k)e^{i(kz-\omega t)}dk + \int_{0}^{-\infty} \tilde{B}(-k)e^{i(-kz+\omega t)}(-dk) \right]\] \[= \mathrm{Re}\left[ \int_{0}^{\infty}\tilde{A}(k)e^{i(kz-\omega t)}dk + \int_{-\infty}^{0} \tilde{B}(-k)e^{-i(kz-\omega t)}dk \right]\] \[=\mathrm{Re}\left[ \int_{0}^{\infty} \tilde{A}(k)e^{i(kz-\omega t)}dk \right] + \mathrm{Re}\left[ \int_{-\infty}^{0}\tilde{B}(-k)e^{-i(kz-\omega t)}dk \right]\]두번째 항은 다음과 같이 만들 수 있다.
\[\mathrm{Re}\left[ \int_{-\infty}^{0}\tilde{B}(-k)e^{-i(kz-\omega t)}dk \right]= \mathrm{Re}\left[ \int_{-\infty}^{0}\tilde{B}(-k)e^{-i(kz-\omega t)}dk \right]\] \[= \mathrm{Re}\left[ \left( \int_{-\infty}^{0}\tilde{B}(-k)e^{-i(kz-\omega t)}dk \right)^* \right]\] \[= \mathrm{Re}\left[ \int_{-\infty}^{0}\tilde{B}^*(-k)e^{i(kz-\omega t)}dk \right]\]따라서 다음과 같다.
\[f(z,t)=\mathrm{Re}\left[ \int_{0}^{\infty}\tilde{A}(k)e^{i(kz-\omega t)}dk + \int_{-\infty}^{0}\tilde{B}^*(-k)e^{i(kz-\omega t)}dk \right]\] \[= \mathrm{Re}\left[ \int_{-\infty}^{\infty}\tilde{C}(k)e^{i(kz-\omega t)} dk\right], ~~~~\tilde{C}(k) \equiv \begin{cases} \tilde{A}(k)& k\geq 0 \\ \tilde{B}^*(-k)&k<0 \end{cases}\]푸리에 정리에 의해, \(e^{i(kz-\omega t)} = e^{ik(z-vt)}=e^{ikx}\)는 \(L_{1}\) or \(L_{2}\) 공간의 모든 함수를 표현한다.
\(k<0\)에 대해 적분하면 결과는 다음과 같다.
\[f(z,t) = \mathrm{Re}\left[ \int_{-\infty}^{0}\tilde{A}e^{i(kz-\omega t)}dk + \int_{-\infty}^{0}\tilde{B}e^{i(kz+\omega t)}dk \right]\]이번엔 첫번째 항의 \(k\)를 \(-k\)로 바꾸고, 같은 논리로 전개하면 다음 단계까지 도달 가능하다.
\[= \mathrm{Re}\left[ \int_{0}^{\infty} \tilde{A}^*(-k)e^{i(kz+\omega t)}dk + \int_{-\infty}^{0}\tilde{B}(k)e^{i(kz+\omega t)}dk \right]\] \[= \mathrm{Re}\left[ \int_{-\infty}^{\infty}\tilde{C}'(k) e^{i(kz+\omega t)}dk \right], ~~~~\tilde{C}'(k) \equiv \begin{cases} \tilde{A}^*(-k) & k \geq 0 \\ \tilde{B}(k) & k < 0 \end{cases}\]Let, \(k \to -k\)
\[= \mathrm{Re}\left[ \int_{\infty}^{-\infty}\tilde{C}'(-k) e^{i(-kz+\omega t)}(-dk) \right]\] \[= \mathrm{Re}\left[ \int_{-\infty}^{\infty}\tilde{C}'(-k)e^{-i(kz-\omega t)}dk \right]\] \[= \mathrm{Re}\left[ \left( \int_{-\infty}^{\infty}\tilde{C}'(-k)e^{-i(kz-\omega t)}dk \right)^* \right]\] \[= \mathrm{Re}\left[ \int_{-\infty}^{\infty}(\tilde{C}'(-k))^*e^{i(kz-\omega t)}dk \right]\]이 함수 또한 푸리에 정리에 의해, \(L_{1}\) or \(L_{2}\) 공간의 모든 함수를 표현한다. 이는 \(k>0\) 적분 결과의 다른 표현일 뿐이다. 두 결과 모두 같은 기저, 모든 \(k\)에 대해 같은 함수 공간을 Span하기 때문이다. 즉, General Solution은 하나의 결과를 사용해도 무방하다.
\[\therefore ~~ f(z,t) = \mathrm{Re}\left[ \int_{-\infty}^{\infty}\tilde{C}(k)e^{i(kz-\omega t)} dk\right]\]3차원 파동 방정식을 어떻게 풀까?
\[\nabla^2 f(x,y,z,t) = \frac{1}{v^2} \frac{\partial^2 f}{\partial t^2}\]변수분리를 해보자.
\[f(x,y,z,t) = X(x)Y(y)Z(z)\Phi(t)\] \[\Phi(X''YZ + XY''Z + XYZ'') = \frac{1}{v^2}XYZ \ddot{\Phi}\] \[\implies \frac{X''}{X} + \frac{Y''}{Y} + \frac{Z''}{Z} = \frac{1}{v^2} \frac{\ddot{\Phi}}{\Phi}\]좌변과 우변이 같으려면, 상수값이어야 한다. 특히 좌변의 합이 상수가 나오려면, 각각의 항 또한 상수어야 한다. 아까와 같이 상수값은 음수어야 의미 있으므로, 다음과 같이 정의하자.
\[\frac{X''}{X} = - k_{x}^2, ~~\frac{Y''}{Y} = - k_{y}^2, ~~ \frac{Z''}{Z} = - k^2_{z}, ~~ \frac{\ddot{\Phi}}{\Phi} = - \omega^2\] \[\implies v^2(k_{x}^2 + k_{y}^2 + k_{z}^2) = \omega^2\] \[\implies \omega = v \lvert \vec{k} \rvert, ~~~\vec{k} = (k_{x}, k_{y}, k_{z})\]일반해는 다음과 같이 쓸 수 있다.
\[f(\vec{r},t) = \mathrm{Re}\left[ \int_{-\infty}^{\infty}dk_{x}\int_{-\infty}^{\infty}dk_{y}\int_{-\infty}^{\infty}dk_{z} \tilde{C}(k_{x},k_{y},k_{z}) e^{i(k_{x}x+k_{y}y+k_{z}z-\omega t)} \right]\] \[= \mathrm{Re}\left[ \int_{-\infty}^{\infty} \tilde{C}(\vec{k}) e^{i(\vec{k} \cdot \vec{r} - \omega(\vec{k}) t)} d^3\vec{k} \right], ~~~~\omega(\vec{k}) = v \lvert \vec{k} \rvert\]복소 파동함수는 다음과 같이 정의한다. 복소 파동함수에서 Real을 취하여 실 파동함수를 구한다.
\[\tilde{f}(\vec{r},t) = \int_{-\infty}^{\infty} \tilde{C}(\vec{k}) e^{i(\vec{k} \cdot \vec{r}) - \omega(\vec{k})t}d^3\vec{k}\]\(\vec{k}\)는 무엇인가?
\(k\)는 파동의 wave number(파수) 와 같다. 만약 \(\vec{k}\) 방향이 \(\hat{z}\) 방향과 같으면, \(\vec{k} \cdot \vec{r} = k_{z}z\)와 같다. \(\hat{z}\) 방향은 파동의 진행방향이다. 즉, \(\vec{k}\)는 파동의 진행방향을 의미한다.
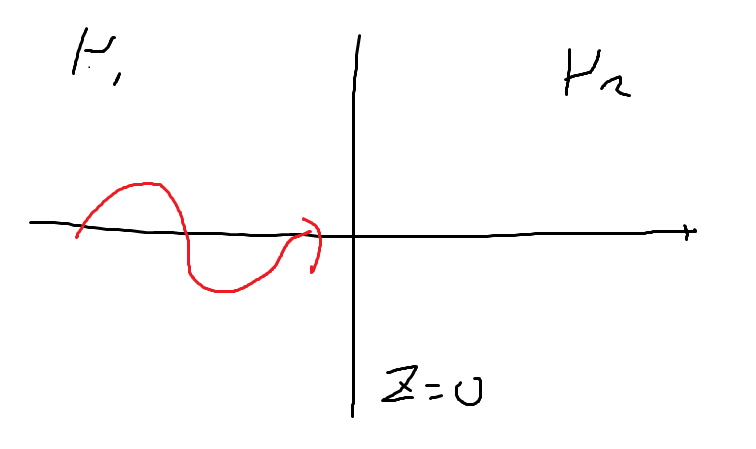
만약 성질이 서로 다른 줄을 연결하면 어떻게 될까?
서로 다른 두 줄 \(\mu_{1}, \mu_{2}\)를 이어붙이고, 그 경계를 \(z=0\)으로 설정한다.
실험 결과, 입사 파동(incident wave)은 경계면을 만나면 경계면에서 반사되는 반사 파동(reflected wave)과 경계면을 뚫고 들어가는 투과 파동(transmitted wave)으로 나뉜다.
입사파가 경계면을 지나 반사파와 투과파로 구분되는 상황의 파동함수 \(f(z,t)\)를 구해보자. 편의상 파동의 진행방향은 \(\vec{k} = \hat{z}k\)로 설정한다.
\(\mu_{1}\) 줄에서 파동의 속도는 \(v_{1} = \sqrt{ \frac{T}{\mu_{1}} }\)이고, \(\mu_{2}\) 줄에서 파동의 속도는 \(v_{2} = \sqrt{ \frac{T}{\mu_{2}} }\)다. 장력은 뉴턴 제3 법칙에 의해 같다. \(\omega\)는 줄을 흔드는 사람이 결정한다. 즉 Source에 의존한다. 줄은 물리적으로 연결되어 있기 때문에 양쪽의 \(\omega\)는 같다. 따라서 \(\omega = v_{1}k_{1} = v_{2}k_{2}\)이다.
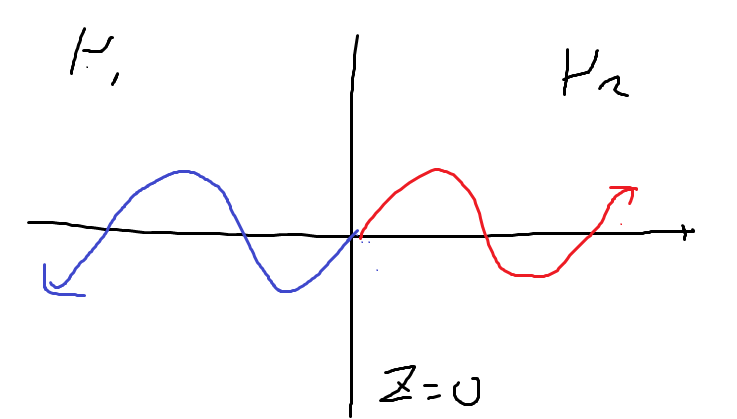
입사 파동은 오른쪽으로 가는 파동이므로 다음과 같다.
\[\tilde{f}_{I}(z,t) = \tilde{A}_{I} e^{i(k_{1}z - \omega t)}\]반사 파동은 왼쪽으로, 투과파동은 오른쪽으로 가는 파동이므로 다음과 같다.
\[\tilde{f}_{R}(z,t) = \tilde{A}_{R}e^{i(-k_{1}z-\omega t)}, ~~\tilde{f}_{T}(z,t) = \tilde{A}_{T}e^{i(k_{2}z-\omega t)}\][!question] 왼쪽으로 가는 파동은 \(e^{i(k_{1}z + \omega t)}\)로 써야하는 것 아닌가?{title} 그렇게 써도 되지만, \(-\omega t\)로 \(t\) 항의 부호를 통일하는게 편리하다. \(k\)의 부호를 바꿔도 진폭, 위상 상수, 진동수, 파장이 모두 동일하지만 반대쪽으로 가는 파동이 만들어진다.
\[\mathrm{Re}[\tilde{A}e^{i(kz-\omega t)}] = A\cos(kz - \omega t + \delta)\]\(k\)의 부호를 바꾸면 다음과 같다.
\[\mathrm{Re}[\tilde{A}e^{i(-kz - \omega t)}] = A\cos (-kz - \omega t + \delta)\] \[= A\cos(kz + \omega t - \delta)\]이는 정확히 위상 \(\delta\)의 파동의 방향이 뒤집힌 결과와 같다.
복소 파동함수는 다음과 같다.
\[\tilde{f}(z,t) = \begin{cases} \tilde{A}_{I} e^{i(k_{1}z - \omega t)} + \tilde{A}_{R}e^{i(-k_{1}z-\omega t)} & z<0 \\ \tilde{A}_{T}e^{i(k_{2}z-\omega t)} & z>0 \end{cases}\]Boundry Condition을 사용하여 계수를 결정해야 한다. 먼저, 물리적으로 파동함수 자체는 \(z=0\)에서 항상 연속이어야 한다.
\[\tilde{f}(0^+, t) = \tilde{f}(0^-, t)\]그리고, 파동의 기울기 \(\frac{\partial f}{\partial z}\)도 연속적이어야 한다. 연속적이지 않은 Boundry는, 질점에 질량이 존재하는 경우라면 연속적이지 않다. 예를들어 구슬을 묶어둔 상태를 상상하면 된다. 그런 것 없이 실의 단위 길이당 질량 \(\mu\)만 정의되어 있다면, 질점은 단위 길이가 0이므로 질량도 0이다. 따라서 파동의 기울기 \(\frac{\partial f}{\partial z}\) 또한 \(z=0\)에서 연속이다.
\[\frac{\partial f(z,t)}{\partial z}\mid_{z=0^+} = \frac{\partial f(z,t)}{\partial z}\mid_{z=0^-}\]두 Boundry Condition을 사용하면 다음과 같다.
\[\tilde{A}_{I} e^{-i\omega t} + \tilde{A}_{R}e^{-i\omega t} = \tilde{A}_{T} e^{-i\omega t} \implies \tilde{A}_{I} + \tilde{A}_{R} = \tilde{A}_{T}\] \[ik_{1}\tilde{A}_{I} - ik_{1}\tilde{A}_{R} = ik_{2}\tilde{A}_{T} \implies k_{1} (\tilde{A}_{I} - \tilde{A}_{R}) = k_{2}\tilde{A}_{T}\]계수가 세개인데 식은 두개이므로, 모든 계수를 하나의 문자로 통일할 수 있다. 이왕이면 반사파와 투과파를 입사파로 표현하는게 좋을 것이다. 두 식을 연립하여 관계를 찾아보자.
\[k_{1}(\tilde{A}_{I} - \tilde{A}_{R}) = k_{2}(\tilde{A}_{I} + \tilde{A}_{R})\] \[\implies (k_{1} - k_{2})\tilde{A}_{I} = (k_{1} + k_{2}) \tilde{A}_{R}\] \[\implies \tilde{A}_{R} = \frac{k_{1} - k_{2}}{k_{1} + k_{2}}\tilde{A}_{I}\] \[\tilde{A}_{T} = \tilde{A}_{I} + \frac{k_{1} - k_{2}}{k_{1} + k_{2}}\tilde{A}_{I}\] \[= \frac{2k_{1}}{k_{1}+k_{2}}\tilde{A}_{I}\]이때, \(\omega = v_{1}k_{1} = v_{2} k_{2}\)이므로 다음 관계에 있다.
\[\frac{k_{1}}{k_{2}} = \frac{v_{2}}{v_{1}}\]따라서 다음과 같이 정리할 수 있다.
\[\therefore ~~ \tilde{A}_{R} = \frac{v_{2} - v_{1}}{v_{1} + v_{2}}\tilde{A}_{I}\] \[\therefore ~~ \tilde{A}_{T} = \frac{2v_{2}}{v_{1} + v_{2}}\tilde{A}_{I}\]실수 진폭과 위상은 다음 관계에 있다.
\[\therefore ~~ A_{R}e^{i \delta_{R}} = \frac{v_{2} - v_{1}}{v_{1} + v_{2}}A_{I}e^{i\delta_{I}}\] \[\therefore ~~ A_{T}e^{i\delta_{T}} = \frac{2v_{2}}{v_{1} + v_{2}}A_{I}e^{i\delta_{I}}\]위 식은 양 변 모두 \(re^{i\theta}\) 꼴의 복소수와 같다. 두 복소수가 같으려면 크기 \(r\)과 복소 평면 위의 위상각 \(\theta\)가 서로 같아야 한다. 따라서, \(\mu_{1}\)과 \(\mu_{2}\)에 관계 없이 항상 다음 관계를 만족한다.
\[A_{R} = \left\lvert \frac{v_{2}-v_{1}}{v_{1}+v_{2}} \right\rvert A_{I}\] \[A_{T} = \frac{2v_{2}}{v_{1}+v_{2}} A_{I}\]위상의 경우 차이가 있다. 만약 \(\mu_{1} > \mu_{2}\)면? \(\mu\)는 \(v^2\)과 반비례하므로 \(v_{1}<v_{2}\)이다. 복소수의 크기의 부호가 같으므로, 위상만 같으면 두 복소수가 같아진다.
\[\delta_{R} = \delta_{T} = \delta_{I}\]만약 \(\mu_{1}<\mu_{2}\)면? \(v_{1}>v_{2}\)고, 이 경우 \(v_{2} - v_{1} < 0\)이다. \(re^{i\theta}\)에서 크기 \(r\)이 음수인 것은 무슨 의미를 갖는가? \(-1\)은 복소 평면 위에 어디 위치하는지 생각해보면, \(-1 = 1 \cdot e^{i\pi}\)와 같다. 따라서, 다음과 같다.
\[-r e^{i\theta} = e^{i\pi} \cdot e^{i\theta} = e^{i(\theta + \pi)}\]즉, 크기가 반대면 위상각이 180도 차이나는 것과 동등하다. 따라서, 다음과 같다.
\[\delta_{R} = \delta_{I} + \pi\] \[\delta_{T} = \delta_{I}\]두번째 줄이 첫번째 줄보다 무거우면, 반사파의 위상이 뒤집힌다.
만약 둘째줄이 아주 무거우면, \(\mu_{1} \ll \mu_{2}\) \(v_{1} \gg v_{2}\)이고, \(v_{2} \simeq 0\)으로 근사된다. 따라서
\[A_{T} \simeq 0, ~~A_{R} \simeq A_{I}\]와 같다. 투과되지 않고 대부분이 반사된다.