기초전자기학 2. 정전기학

건국대학교 여준현 교수님의 전자기학1 수업을 정리한 내용입니다. 교재: Introduction to electrodynamics, David J. Griffths (4판)

Electricity (전기)

전기란, 전하가 흐름에 따라 발생하는 물리 현상이다. 번개, 정전기, 전류, 통신 등등…

Electric charge (전하)

양성자와 전자가 가지는 고유한 성질. 모든 물질은 질량이라는 고유한 성질을 가지고, 질량을 가진 입자는 서로를 끌어당긴다. 라는 특징이 있듯이, 양성자와 전자 또한 질량과 같은 고유한 성질을 가지고, 전하를 가진 입자는 서로 끌어당기거나 미는 특징이 있다.

Maxwell’s equations (맥스웰 방정식)

• \(\displaystyle \nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_{0}}\)
• \(\displaystyle \nabla \cdot \mathbf{B} = 0\)
• \(\displaystyle \nabla \times \mathbf{E} = - \frac{ \partial \mathbf{B} }{ \partial t }\)
• \(\displaystyle \nabla \times \mathbf{B} = \mu_{0} \left( \mathbf{J} + \epsilon_{0} \frac{ \partial \mathbf{E} }{ \partial t } \right)\)

전자기학은 위 네가지 식으로 모두 설명된다. 이를 맥스웰 방정식이라고 한다. 각각 식의 의미는 다음과 같다.

1. 플러스 전하는 전기장을 내뿜고 마이너스 전하는 전기장을 빨아들인다.
2. 자석은 N극과 S극을 완전히 분리할 수 없기 때문에, N극에서 나온 자기장은 다시 S극으로 빨려들어간다. 따라서 발산이 없다.
3. 자석을 막 움직이면 주위에 회전하는 전기장이 생긴다.
4. 전류가 흐르면 그 주위로 자기장이 회전하면서 생긴다

ElectricStatics, MagneticStatics에선 맥스웰 방정식이 다음과 같이 단순화된다.

• \(\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_{0}}\)
• \(\nabla \cdot \mathbf{B} = 0\)
• \(\nabla \times \mathbf{E} = 0\)
• \(\nabla \times \mathbf{B} = \mu_{0} \mathbf{J}\)

[!question]- 전기와 자기의 근원은 무엇인가?{title} 3번 식에 \(\nabla \times\)를 곱하고 식을 연립해보자.

\[\displaystyle \nabla \times (\nabla \times \mathbf{E}) = - \frac{ \partial }{ \partial t }(\nabla \times \mathbf{B})\] \[\displaystyle \nabla(\nabla \cdot \mathbf{E}) - \nabla^2 \mathbf{E} = - \mu_{0} \frac{ \partial }{ \partial t } \mathbf{J} - \mu_{0} \epsilon_{0} \frac{ \partial^2 \mathbf{E} }{ \partial t^2 }\] \[\displaystyle \nabla^2 \mathbf{E} - \mu_{0} \epsilon_{0} \frac{ \partial^2 \mathbf{E} }{ \partial t^2 } = 0\]

갑자기 파동 방정식이 튀어나온다. 이 파동의 속도를 한번 구해봤더니, 빛의 속도가 나왔다…

전기장 식과 자기장 식을 연립해서 풀었더니 빛의 속도가 나왔다고?

\[\therefore~\text{전기와 자기가 얽혀서 진동하는 파동} = \text{빛}\]

Coulomb’s law

• \(\displaystyle \vec{F} = \frac{1}{4\pi\epsilon_{0}} \frac{qQ}{\eta^2}\hat{\eta}\)

두 전하 \(q\), \(Q\) 사이에 작용하는 힘을 쿨롱 법칙으로 설명한다. 이때 \(\epsilon_{0}\)는 유전 상수고 \(\displaystyle 8.85 \times 10^{-12} \frac{C^2}{N \cdot m^2}\)와 같다. \(\hat{\eta}\)는 분리 벡터다. 이는 실험으로 찾아낸 공식이다.

Separation vector (분리 벡터)

• \(\vec{\eta} \equiv \vec{r} - \vec{r}'\)
  • \(\vec{r}\) : Test Point
  • \(\vec{r}'\) : Source Point

전자기학에서 전기장을 만드는 Source Point와 Test Point 두개의 값을 다루는 일이 많다. Source Point \(\to\) Field Point의 의미를 갖는 벡터는 많이 사용하고, 이 벡터를 따로 이름을 붙여 Separation Vector (분리 벡터) 라고 한다.

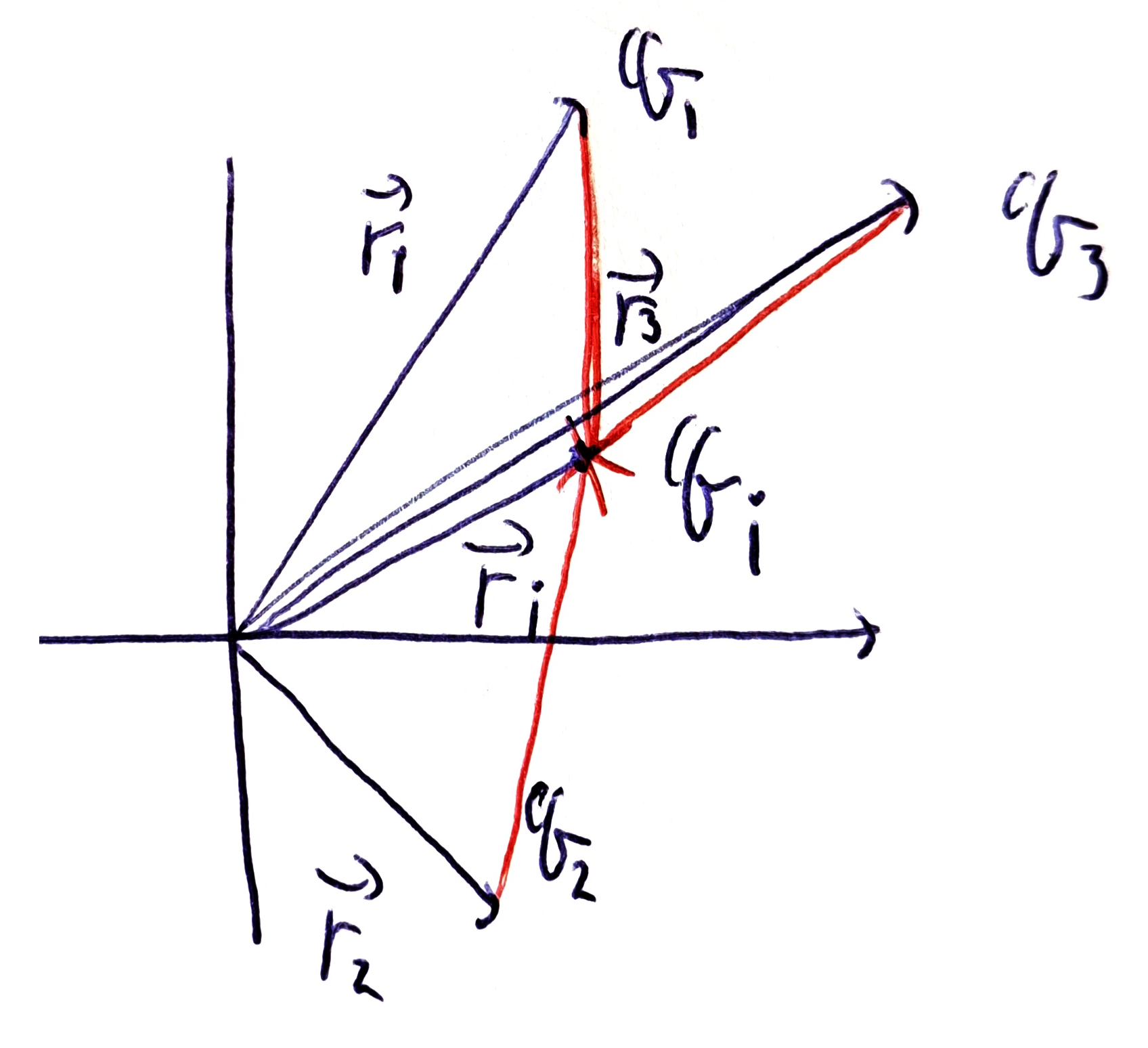
Superposition principle (중첩 원리)

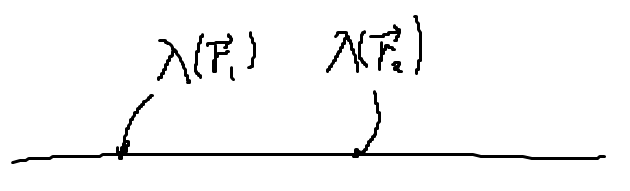
시험 전하 Q가 받는 힘은, 낱낱의 원천전하가 주는 힘을 더한것과 같다.

\[\vec{F} = \vec{F}_{1} + \vec{F}_{2} + \dots\]

양 변을 Q로 나누면, 전기장도 중첩 원리를 따른다는 것을 알 수 있다.

\[\vec{E} = \vec{E}_{1} + \vec{E}_{2} + \dots\]

즉 전기장은 낱낱의 원천전하가 만드는 전기장의 합과 같다. 공통의 기준으로부터 \(\vec{r}\)까지 선적분하면, 추후 등장하는 개념인 전위 또한 중첩원리를 따른다는 것을 알 수 있다.

\[- \int^{\vec{r}}_{O} \vec{E} \cdot d\vec{r} = - \int^{\vec{r}}_{O} (\vec{E}_{1} + \vec{E}_{2} + \dots) \cdot d\vec{r}= - \int^{\vec{r}}_{O} \vec{E}_{1} \cdot d\vec{r} - \int^{\vec{r}}_{O} \vec{E}_{2} \cdot d\vec{r} - \dots\] \[\implies V = V_{1} + V_{2} + \dots\]

Electric Field (전기장)

• \(\displaystyle \vec{E}(\vec{r}) = \frac{1}{4\pi \epsilon_{0}} \frac{q}{\eta^2} \hat{\eta}\) : 점전하 \(q\)가 만드는 전기장.
• \(\displaystyle \vec{E}(\vec{r}) = \frac{1}{4\pi \epsilon_{0}} \sum_{i=1}^{n} \frac{q_{i}}{\eta^2_{i}} \hat{\eta}_{i}\) : 여러개의 전하 \(q_{1}, q_{2}, \dots, q_{n}\)이 만드는 전기장.
• \(\displaystyle \vec{E}(\vec{r}) = \frac{1}{4\pi \epsilon_{0}} \int \frac{1}{\eta^2}\hat{\eta} dq\) : 연속 전하 분포가 만드는 전기장.
• \(\vec{F}(\vec{r}) = q \vec{E}(\vec{r})\)

Field라는 컨셉을 도입하여, 전기적 현상을 더 쉽게 설명할 수 있다. 무수히 많은 전하의 서로 상호작용을 하나하나 분석하는 것보다는, 무수히 많은 전하가 하나의 전기장을 만들고, 그 전기장을 구하는 것이 훨씬 쉽다. 전기장을 만드는 전하를 Source Charges (\(q\))라고 하며, 전기장 위에 올리는 Test Charge는 영향을 받는다.

전하를 가진 입자는 전기장을 만들며, 전기장 위에 전하를 가진 입자는 영향을 만든다. 전기장 위에 입자를 올리면, 그 입자가 받는 힘은 \(\vec{F} = q\vec{E}\)와 같다.

중첩 원리에 따라 여러개의 점전하가 만드는 전기장은 각각 점전하가 만드는 전기장의 합과 같으므로, \(\vec{E} = \vec{E}_{1} + \vec{E}_{2} + \dots + \vec{E}_{n} = \frac{1}{4\pi \epsilon_{0}} \sum_{i=1}^{n} \frac{q_{i}}{\eta^2_{i}} \hat{\eta}_{i}\)와 같다.

전하가 어떤 영역에서 연속적으로 퍼져있다면, 미소 전하 \(dq\)를 Sum하여 구할 수 있다. 따라서 \(\displaystyle \vec{E}(\vec{r}) = \frac{1}{4\pi \epsilon_{0}} \int \frac{\hat{\eta}}{\eta^2} dq\)와 같다. 이때 미소전하 \(dq\)는 (전하 밀도 x 미소 영역 (\(dl, dA, dV\)))를 통해 구할 수 있다.

• \(dq = \lambda(\vec{r}) dl\) : 전하가 선을 따라 분포함
• \(dq = \sigma(\vec{r})dA\) : 전하가 면을 따라 분포함
• \(dq = \rho(\vec{r}) = dV\) : 전하가 체적을 따라 분포함

Charge density (전하 밀도)

길이, 면적, 부피당 전하량을 의미한다. 길이당 전하량은 선전하 밀도 (\(\lambda\)), 면적당 전하량은 면전하 밀도(\(\sigma\)), 부피당 전하량은 부피전하 밀도(\(\rho\)) 라고 한다.

선전하 밀도

• \(\displaystyle Q_{total} = \int_0^L \lambda(\vec{r}) dl\)

전하가 선을 따라 분포하고 있다면, \(\lambda(\vec{r})\) 함수를 사용하여 표현한다. 일반적인 경우 전하가 균일하게 분포하지 않으므로, \(\vec{r}_{1}\)에 위치한 전하 밀도와 \(\vec{r}_{2}\)에 위치한 전하 밀도가 같지 않을 것이므로, 함수를 사용한다. 만약, 전하가 균일하게 분포하고 있다면 밀도 함수는 상수가 된다. (\(\lambda(\vec{r}) = \lambda\))

만약 길이 0부터 L까지 총 전하량을 알고싶다면, 아주 작은 단위 \(\lambda(\vec{r}) \cdot dl\)로 나눠서 Sum하면 된다.

면전하 밀도

• \(\displaystyle Q_{total} = \int_S \sigma(\vec{r}) dA\)

전하가 면을 따라 분포하고 있다면, \(\sigma(\vec{r})\) 함수를 사용하여 표현한다. 만약, 전하가 균일하게 분포하고 있다면 밀도 함수는 상수가 된다. (\(\sigma(\vec{r}) = \sigma\)) 만약 면적 내 총 전하량을 알고싶다면, 아주 작은 단위 \(\sigma(\vec{r}) \cdot d \vec{a}\)로 나눠서 Sum하면 된다.

부피전하 밀도

• \(\displaystyle Q_{total} = \int_V \rho(\vec{r}) dV\)

전하가 부피를 따라 분포하고 있다면, \(\rho(\vec{r})\)함수를 사용하여 표현한다. 만약, 전하가 균일하게 분포하고 있다면 밀도 함수는 상수가 된다. (\(\rho(\vec{r}) = \rho\)) 만약 부피 내 총 전하량을 알고싶다면, 아주 작은 단위 \(\rho(\vec{r}) \cdot dV\)로 나눠서 Sum하면 된다.

점전하 밀도

• \(\rho(\vec{r}) = q_{1} \delta^3(\vec{r} - \vec{r}_{1}) + q_{2} \delta^3 (\vec{r} - \vec{r}_{2}) + \dots\)

점전하는 Delta Function를 사용해서 밀도함수 \(\rho(\vec{r})\)로 표현할 수 있다.

Gauss’s law (가우스 법칙)

• \(\displaystyle \oint_{S} \vec{E} \cdot d\vec{a} = \frac{Q_{all}}{\epsilon_{0}}\)
• \(\displaystyle \nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}}\)

닫힌곡면을 지나는 선속 (Flux)이 그 속에 들어있는 총 전하량의 지표가 될 수 있다. 전하가 여러개가 아니라면, 모든 전하를 감싸는 닫힌 곡면으로 생각하면 된다.

[!question]- Why?{title} 총 전기장은 낱낱의 전하가 만드는 전기장의 합과 같다.

\[\vec{E} = \sum_{i=1}^{n} E_{i}\]

모든 전하를 감싸는 곡면을 지나는 선속은 다음과 같다.

\[\oint_{S} \vec{E} \cdot d\vec{a} = \oint_{S} \sum_{i=1}^{n} \vec{E_{i}} \cdot d\vec{a}\] \[= \sum_{i=1}^{n} \oint_{S} \vec{E}_{i} \cdot d \vec{a}= \sum_{i=1}^{n} \frac{q_{i}}{\epsilon_0} = \frac{Q_{all}}{\epsilon_{0}}\]

[!note]- 발산 정리를 써서 미분방정식으로 바꿀 수 있다.{title}

\[\oint_{S} \vec{E} \cdot d \vec{a} = \int_{V} (\nabla \cdot \vec{E}) dV\]

\(Q_{all}\)은 \(\int_{V} \rho dV\)와 같으므로

\[\int_{V} (\nabla \cdot \vec{E})dV = \int_{V} \frac{\rho}{\epsilon_{0}} dV\] \[\implies \nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}}\]

[!note]- 직접 전기장의 발산 계산해보기{title}

\[\vec{E} = \frac{1}{4\pi \epsilon_{0}} \int \frac{\hat{\eta}}{\eta^2} dq\]

부피 내 전하가 일반적인 상황이므로, \(dq = \rho(\vec{r})dV\)를 사용하자.

\[\vec{E} = \frac{1}{4\pi \epsilon_{0}} \int_{V} \frac{\hat{\eta}}{\eta^2} \rho(\vec{r}) dV\] \[\nabla \cdot \vec{E} = \nabla \cdot \frac{1}{4\pi \epsilon_{0}} \int_{V} \frac{\hat{\eta}}{\eta^2} \rho(\vec{r}) dV\]

\(\frac{1}{4\pi \epsilon_{0}} \int_{V} \frac{\hat{\eta}}{\eta^2} \rho(\vec{r}) dV\) 요소중 벡터는 \(\frac{\hat{\eta}}{\eta^2}\) 뿐이므로, 미분 연산자를 안에 넣어 직접 미분한다.

\[= \frac{1}{4\pi \epsilon_{0}} \int_{V} \nabla \cdot \left( \frac{\hat{\eta}}{\eta^2} \right) \rho(\vec{r}) dV\] \[\nabla \cdot \left( \frac{\hat{\eta}}{\eta^2} \right) = 4\pi \delta^3(\vec{\eta})\]

이므로

\[= \frac{1}{4\pi \epsilon_{0}} \int_{V} 4\pi \delta^3(\vec{\eta}) \rho(\vec{r}) dV\] \[= \frac{1}{\epsilon_{0}} \int_{V} \delta^3(\vec{r} - \vec{r}') \rho(\vec{r}) dV\] \[= \frac{1}{\epsilon_{0}} \rho(\vec{r})\]

핵심은 균일하고 대칭성이 있는 전기장은, 가우스 곡면 면적분 내에서 상수 취급할 수 있다는 것이다.

[!example]- 전하가 고르게 퍼진 반지름 R인 공이 만드는 전기장을 구하라{title}

구를 감싸는 임의의 가우스 곡면을 생각해보자.

\[\oint_{S} \vec{E} \cdot d\vec{a} = \int_{0}^{\pi}\int_{0}^{2\pi} \lvert \vec{E} \rvert \cdot r^2\sin \theta d\phi d\theta\]

이때, \(\vec{E}\)가 균일하고 대칭성이 있다면, \(\vec{E}\)의 크기는 가우스 곡면에서 일정하다. 따라서 \(\lvert \vec{E} \rvert\)를 적분 밖으로 꺼낼 수 있다.

\[= \lvert \vec{E} \rvert\int_{0}^{\pi}\int_{0}^{2\pi} r^2\sin \theta d\phi d\theta\] \[= \lvert \vec{E} \rvert 4\pi r^2 = \frac{q}{\epsilon_{0}}\] \[\therefore ~ \vec{E} = \frac{1}{4\pi \epsilon_{0}} \frac{q}{r^2} \hat{r}\]

[!example]- Example 1{title}

\[\displaystyle \oint \vec{E} \cdot d \vec{a} = E \cdot A + E \cdot A = \frac{1}{\epsilon_{0}}Q \implies E = \frac{1}{\epsilon_{0} \frac{Q}{2A}} = \frac{\sigma}{2 \epsilon_{0}}\]

[!example]- Example 2{title}

\[\displaystyle \oint \vec{E} \cdot d \vec{a} = E \cdot 2\pi s \cdot L\] \[\implies Q_{inside} = \int dv \rho = \int_{0}^{S} ds' s' \int_{0}^{2\pi} d \phi' \int_{0}^{L} dz' ks' = 2\pi L \cdot \frac{{ks^3}}{3}\] \[\displaystyle \therefore ~E = \frac{k}{3 \epsilon_{0}} s^2\]

Gaussian surface (가우스 곡면)

가우스 곡면이란 대칭성을 갖고, 모든 전하를 감싸는 닫힌 곡면이다. 가우스 곡면의 종류는 다음과 같다.

1. 중심이 일치하는 공 (구 대칭성)
2. 중심축이 일치하는 원통 (원통 대칭성)
3. 면을 품는 동전 모양

전기장의 Curl

• \(\nabla \times \vec{E}(\vec{r}) = \vec{0}\)

원점에서 전하가 q인 점전하가 만드는 전기장을 \(\vec{a}\)부터 \(\vec{b}\)까지 선적분 해보자.

\[\int^{\vec{b}}_{\vec{a}} \vec{E} \cdot d \vec{r} = \frac{1}{4\pi \epsilon_{0}} \int^\vec{b}_{\vec{a}} \frac{q}{r^2} dr= -\frac{1}{4\pi \epsilon_{0}} \left[ \frac{q}{r} \right]^{r_{b}}_{r_{a}} = \frac{1}{4\pi \epsilon_{0}} \left( \frac{q}{r_{a} - \frac{q}{r_{b}}} \right)\]

\(d \vec{r} = dr \hat{r} + r d \theta \hat{\theta} + r\sin \theta d\phi \hat{\phi}\) 이고, 내적하면 \(\hat{\theta}\)과 \(\hat{\phi}\)는 날아가고 \(\hat{r}\) 성분만 남는다. \(r_{a}\)와 \(r_{b}\)는 원점에서 \(\vec{a}\)와 \(\vec{b}\)까지의 거리이다. 만약 닫힌 곡선에 대해 선적분하면 \(r_{a} = r_{b}\)이므로 명백히 0이다. \(\displaystyle \oint \vec{E} \cdot d \vec{r} = 0\) 스토크스 정리에 의해 다음 값 또한 0이다.

\[\therefore ~ \displaystyle \int_{S} (\nabla \times \vec{E}) d\vec{a} = 0 \implies \nabla \times \vec{E} = \vec{0}\]

전기장을 쉽게 계산하는 방법

우리가 측정할 수 있는것은, 전하 분포밖에 없다. 전하 분포를 통해 전기장을 구할 수 있는 일반적인 식이 존재하긴 하지만, 적분이 너무 복잡하다. 이 적분을 피하거나 요령껏 푸는게 정전기학에서 하는 대부분이다.

1. 전기장이 대칭성이 있다면 : 가우스 법칙을 쓰면 된다.
2. 전위를 계산해서 전기장을 얻는 방법 : 전위를 구하고, \(\vec{E} = -\nabla V\) 관계를 통해 전기장을 얻을 수 있다.

점전하 분포가 갖는 총 에너지를 구하는 방법

• \(\displaystyle W = \frac{1}{2} \sum_{i=1}^{n}q_{i} V(\vec{r}_{i})\)

전하가 전기장 위에 있다면, 위치 에너지를 갖는다. 모든 점전하가 갖는 에너지의 합은 어떻게 계산할 수 있을까? 전하를 아주 먼곳에서 하나씩 가져오는 것을 상상해보자. 처음에 전하 \(q_{1}\)을 가져올 때는 전기장이 없으므로 일이 들지 않는다.

\[W_{1}=0\]

이후 전하 \(q_{2}\)를 가져올 때는 \(q_{1}\)이 전기장을 만든다. 그 전기장 내에서 \(q_{2}\) 전하를 \(\vec{r}\) 위치에 가져다 놓기 위해 필요한 에너지는 \(W = Q V(\vec{r})\)이다. 전위는 \(\displaystyle V(\vec{r}) = \frac{1}{4\pi \epsilon_{0}} \frac{q_1}{\eta}\)이므로 다음과 같다.

\[W_{2} = \frac{q_{2}}{4\pi \epsilon_{0}} \frac{q_{1}}{\eta}\]

다음 전하 \(q_{3}\)을 가져오는데 필요한 에너지는 똑같이 \(W = Q V(\vec{r})\)다. 이때 전위는, \(q_{1}\)과 \(q_{2}\)가 전기장을 만들고, 중첩 원리에 따라 \(q_{1}\)과 \(q_{2}\)가 만드는 전위는 각 점전하가 만드는 전위의 합과 같다.

\[V(\vec{r}) = \frac{1}{4\pi \epsilon_{0}} \left( \frac{q_{1}}{\eta_{13}} + \frac{q_{2}}{\eta_{23}} \right)\]

따라서 \(q_{3}\)을 가져오는데 필요한 에너지는 다음과 같다.

\[W_{3} = \frac{q_{3}}{4\pi \epsilon_{0}} \left( \frac{q_{1}}{\eta_{13}} + \frac{q_{2}}{\eta_{23}} \right)\]

똑같은 원리로, 다음 \(q_{4}\)를 가져오는데 필요한 에너지는 다음과 같다.

\[W_{4} = \frac{q_{4}}{4\pi \epsilon_{0}} \left( \frac{q_{1}}{\eta_{14}} + \frac{q_{2}}{\eta_{24}} + \frac{q_{3}}{\eta_{34}} \right)\]

\(q_{1}\) ~ \(q_{4}\)를 해당 위치에 셋팅하는데 필요한 총 에너지는 다음과 같다.

\[W = W_{1} + W_{2} + W_{3} + W_{4}\] \[= \frac{1}{4\pi \epsilon_{0}} \left( \frac{q_{1}q_{2}}{\eta_{12}} + \frac{q_{1}q_{3}}{\eta_{13}} + \frac{q_{2}q_{3}}{\eta_{23}} + \frac{q_{1}q_{4}}{\eta_{14}} + \frac{q_{2}q_{4}}{\eta_{24}} + \frac{q_{3}q_{4}}{\eta_{34}} \right)\] \[= \frac{1}{4\pi \epsilon_{0}} \left( \frac{q_{1}q_{2}}{\eta_{12}} + \frac{q_{1}q_{3}}{\eta_{13}} + \frac{q_{1}q_{4}}{\eta_{14}} + \frac{q_{2}q_{3}}{\eta_{23}} + \frac{q_{2}q_{4}}{\eta_{24}} + \frac{q_{3}q_{4}}{\eta_{34}} \right)\]

규칙을 통해 일반화하면 다음과 같다.

\[W= \frac{1}{2} \frac{1}{4\pi\epsilon_{0}} \sum_{i=1}^{n} \sum_{j=1, i \neq j}^{n} \frac{{q_{i} q_{j}}}{\eta_{ij} }= \frac{1}{2} \sum_{i=1}^{n} q_{i} \left( \frac{1}{4\pi \epsilon_{0}} \sum_{j=1, j\neq i}^{n} \frac{q_{j}}{\eta_{ij}} \right)\]

괄호 안의 항은 \(q_{i}\) 지점에서 \(q_{i}\)를 제외한 다른 모든 전하가 만드는 전위의 합과 같다. 이걸 \(V(\vec{r}_{i})\)라고 표현하면 최종 식은 \(\displaystyle W = \frac{1}{2} \sum_{i=1}^{n}q_{i} V(\vec{r}_{i})\)이다. 이것이 점전하를 모으는데 필요한 일의 양이며, 전하 무리가 갖는 총 에너지라고 볼 수 있다.

전기장의 에너지를 구하는 방법

• \(\therefore ~ W = \frac{\epsilon_{0}}{2} \int_{\text{all space}} E^2 d\tau\)

이는 연속 전하 분포가 갖는 에너지를 구하는 것과 관련있다. 만약 전하가 연속적으로 분포되어 있을 때, 그 전하들을 모으는데 필요한 일의 양은 점전하를 모으는데 필요한 일의 양을 계산하는 방법에서, 단위 전하로 바꾸기만 하면 된다.

\[W = \frac{1}{2} \int V dq\]

[!question]- 잠깐! 점전하의 \(V(r_{i})\) 식은 \(q_{i}\)가 제외된 전위인데?{title}

\[W = \frac{1}{2} \sum_{i=1}^{n}q_{i} V(\vec{r}_{i})\]

여기서 \(V(r_{i})\)은 정확히는 \(q_{i}\)를 제외한 나머지 전하들이 \(\vec{r}\)에 만드는 전위다.

그런데 연속된 분포에서는, \(dq\) 하나가 빠지던 말던 큰 차이가 없다.

전하가 부피 영역에서 분포해있으면 \(\displaystyle W = \frac{1}{2} \int V \rho d \tau\)와 같다. 가우스 법칙을 사용해서 \(\rho\)를 \(\nabla \cdot \vec{E}\)로 바꿀 수 있다. \(\displaystyle = \frac{1}{2} \int \epsilon_{0} V(\nabla \cdot \vec{E}) d\tau\) \(V(\nabla \cdot \vec{E})\)는… \(\nabla \cdot (V\vec{E})\)를 곱의 미분법을 하면 나올 것 같다.

\[\nabla \cdot (V \vec{E}) = \nabla V \cdot E + V (\nabla \cdot \vec{E})\] \[\implies V(\nabla \cdot \vec{E}) = \nabla \cdot (V \vec{E}) - \nabla V \cdot \vec{E}\]

따라서, \(\displaystyle W = \frac{\epsilon_{0}}{2} \int \nabla \cdot (V \vec{E}) d\tau - \int\nabla V \cdot \vec{E} d\tau= \frac{\epsilon_{0}}{2} \left(\oint_{S} (V \vec{E}) \cdot d \vec{a} + \int \vec{E}^2 d\tau \right)\)와 같다. 앞의 항의 닫힌 곡면 S는 내 마음대로 잡을 수 있다. \(V\vec{E}\)를 포함하기만 하면 된다. S를 무한히 크게 넓히면, 그곳에서 전위값 \(V=0\)이므로, 면적분 결과도 0이다.

\[\therefore ~ W = \frac{\epsilon_{0}}{2} \int_{\text{all space}} E^2 d\tau\]

전기장 \(\vec{E}(\vec{r})\)가 갖는 총 에너지는 위 식으로 구할 수 있겠다.

[!example]- uniform charge, sphrial shell{title}

\[V(\vec{r} )= \frac{{1}}{4\pi \epsilon_{0}} ~ \begin{cases}~ \frac{q}{r} & \text{if } r \leq R\\~ \frac{q}{R} & \text{if } r > R\end{cases}\]

이므로

\[W = \frac{1}{2} \int \rho V dV= \frac{1}{2} \int \sigma V dA\] \[= \frac{1}{2} \cdot \frac{q}{4\pi R^2} \int \frac{1}{4\pi \epsilon_{0}} \frac{q}{R} da\] \[= \frac{1}{2} \frac{q}{4\pi R^2} \frac{1}{4\pi \epsilon_{0}} \frac{q}{R} 4\pi R^2\] \[= \frac{q^2}{8\pi \epsilon_{0} } \frac{1}{R}\]

이런 구의 전기장은 다음과 같다.

\[\vec{E}= \frac{{1}}{4\pi \epsilon_{0}} ~ \begin{cases}~ \frac{q}{r^2} \hat{r} & \text{if } r > R\\~ 0 & \text{if } R > r\end{cases}\]

내부의 전기장은 0이다. 왜 내부의 전기장은 0일까?

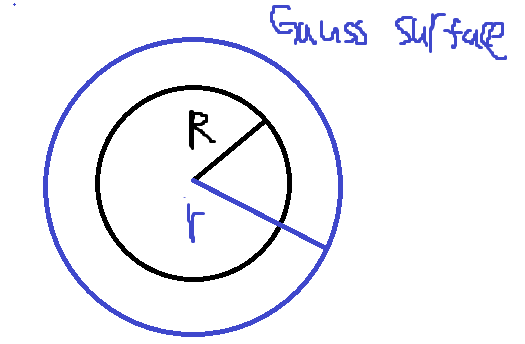
내부에 가상의 가우스 Surface를 잡아보자

가우스 곡면의 반지름을 a라고 하면

\[\oint_{S} \vec{E} \cdot d \vec{a} = E 4\pi a^2 = \frac{q_{inside}}{\epsilon_{0}}\]

그런데 내부의 전하가 없으므로 \(q_{inside}=0\)이다. 따라서 전기장이 0이다. 이런 애매한 직관을 수학으로 명확히 이해할 수 있다.

전기장으로 구해보자

\[W = \frac{\epsilon_{0}}{2} \int \vec{E}^2 dV\] \[= \frac{\epsilon_{0}}{2} \int_{R}^{\infty} \frac{q^2}{4\pi \epsilon_{0}}^2 \frac{1}{r^4} 4\pi r^2dr\] \[= \frac{\epsilon_{0}}{2} \frac{{q^2 4\pi}}{(4\pi \epsilon_{0})^2} \int_{R}^{\infty} \frac{dr}{r^2}\] \[= \frac{1}{2} \frac{q^2}{4\pi \epsilon_{0}} \frac{1}{R}\]

[!example]- 점전하가 만드는 전기장의 에너지{title}

\[E= \frac{q}{4\pi \epsilon_{0}} \frac{1}{r^2}\]

이고, 이 전기장이 갖는 에너지를 계산해보면

\[W = \frac{\epsilon_{0}}{2} \int \vec{E}^2dV\] \[= \frac{\epsilon_{0}}{2} \int\frac{q^2}{(4\pi\epsilon_{0})^2} \frac{1}{r^4} dV\] \[= \frac{\epsilon_{0}}{2} \frac{q^2}{(4\pi \epsilon_{0})^2} \int_{0}^{\infty} 4\pi r^2 \frac{1}{r^4}dr\]

그런데

\[\int_{0}^{\infty} \frac{1}{r^2}dr = \left[ - \frac{1}{r} \right]^\infty_{0} = \infty\]

왜 Infinty가 나올까?

사실 물리적으로 당연하다.

사이즈가 0인 점에 전하를 몰아 넣는것은 말도 안되고, 이론상 Infinity 에너지가 든다. 점전하라는 개념 자체가 우리가 생각하기 편하도록 만든 임의의 개념이기 때문

Conductor (도체)

전자가 원자에 묶여 잘 움직일 수 없는 물질이 절연체(insulator) 또는 유전체고, 전자가 원자에서 튀어나와 자유롭게 움직일 수 있는 것이 도체(conductor) 이다. 도체의 특징은 다음과 같다.

• 도체 내부의 전기장은 0이다.

[!question]- Why?{title}

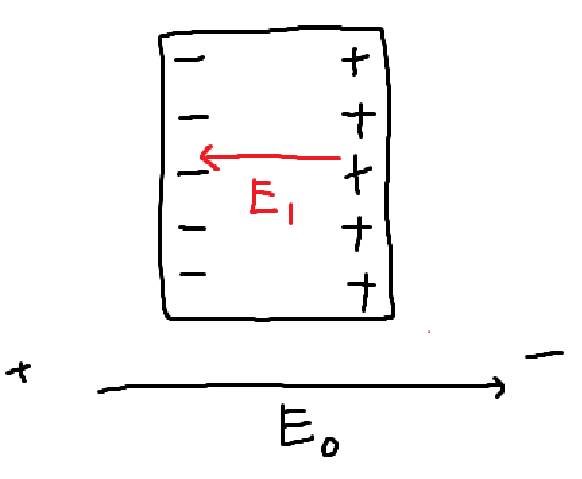
전기장의 + 쪽에 -전하가 몰리게 되고, - 쪽에 + 전하가 몰리게 된다. 이러한 전하 분포에 의해 도체 내부에도 전기장이 걸리게 되고, 항상 외부의 전기장과 상쇄되는 방향으로 만들어진다.

외부에 의한 전기장이 남아있으면, 그 전기장의 영향을 받아 전하가 계속 움직일 것이다. 따라서 외부의 전기장이 완전히 상쇄될 때까지 전하가 움직인다.

외부의 전기장과 내부의 전기장이 완전히 상쇄되면, 도체 내부의 총 전기장은 0이 된다.

따라서 도체 내부의 전하는 외부 전기장이 모두 상쇄될 때 까지 움직이므로 항상 도체의 내부 전기장이 0이다.

• 따라서 도체 내부의 전하 밀도는 0이다. : \(\rho = 0\)

[!question]- Why?{title} 도체 내부의 임의의 가우스 곡면을 잡아보자. 전기장이 0이므로, 가우스 곡면을 뚫고 나오는 전기장의 Flux도 0이다. 따라서 가우스 곡면 내부의 전하량도 0이다.

\[\oint_{S} \vec{E} \cdot d \vec{a} = \frac{q}{\epsilon_{0}}\]

가우스 곡면을 꼭 대칭으로 잡지 않아도, 이를 만족한다. 가우스 곡면을 점점 늘려서, 도체의 Surface 바로 직전까지 늘릴 수 있고, 그 안의 \(Q_{inside}\)는 모두 0이다.

이것의 의미하는 바는 무엇인가? 모든 전하는 표면에만 몰려있다.

• 알짜 전하(net charge)는 표면에 몰려있다.

• 도체 내부의 전위는 상수값이다. : \(\vec{E} = -\nabla V\)

• 도체 바로 밖의 \(\vec{E}\)는 표면에 항상 수직이다.

[!question]- Why?{title} 도체 경계면을 기준으로 내부에서 바로 들어가는 전기장의 평행 성분과, 바로 나오는 전기장의 평행 성분은 같다.

이때, 도체 내부에서 바로 들어가는 전기장은 0이므로, 바로 나오는 전기장은 수직 성분만 존재한다.

그 값은, \(\frac{\sigma}{\epsilon_{0}} \hat{n}\)와 같다.

• 도체 바로 바깥의 전기장은 \(\displaystyle \vec{E} = \frac{\sigma}{\epsilon_{0}} \hat{n}\)와 같다.

• 전기장 또는 전위를 알고있으면, 도체 표면의 전하를 계산할 수 있다.
  1. \(\sigma = E \epsilon_{0}\)
  2. \(\displaystyle \sigma = - \epsilon_{0} \frac{{\partial V}}{\partial n}\)
• 전기장이 있으면, 면전하는 힘을 받는다. 단위 면적이 받는 힘은 \(\displaystyle \vec{f} = \sigma \cdot \frac{1}{2} (\vec{E}_{above} + \vec{E}_{below})\)와 같다.

[!question]- Why?{title} 전기장을 알면 전하가 받는 힘을 계산할 수 있음.

\[\vec{F} = Q \vec{E}\]

\(\sigma = \frac{Q}{A}\)이고, 단위 면적이라고 하면 A=1이다.

\[\vec{f} = \sigma \vec{E}\]

전기장이 불연속적인데, 이때 사용되는 \(\vec{E}\)는 어떤 값을 사용해야 하는가?

총 전기장은 단위 면적이 만드는 전기장 + 나머지가 만드는 전기장으로 구분할 수 있다.

\[\vec{E} = \vec{E}_{\text{조각}} + E_{\text{나머지}}\]

조각은 스스로에게 힘을 줄 수 없다. 자기 몸을 자기가 밀어서 움직일 수 없는 것과 같이.

따라서 조각이 받는 힘은 오직 \(E_{\text{나머지}}\)에 의한 것이다.

위 전기장과 아래 전기장의 차이는 \(\frac{\sigma}{\epsilon_{0}} \hat{n}\)과 같으므로 다음과 같다.

\[E_{above} = E_{\text{나머지}} + \frac{\sigma}{2 \epsilon_{0}} \hat{n}\] \[E_{below} = E_{\text{나머지}} - \frac{\sigma}{2 \epsilon_{0}} \hat{n}\] \[\implies E_{\text{나머지}} = \frac{1}{2} (E_{above} + E_{below})\]

따라서, 계산에 사용되는 전기장은 위쪽 전기장과 아래쪽 전기장의 평균값이다.

\[\vec{f} = \sigma \cdot \frac{1}{2} (\vec{E}_{above} + \vec{E}_{below})\]

도체 면전하의 안쪽 전기장은 항상 0이고, 바깥 전기장은 항상 \(\frac{\sigma}{\epsilon_{0}} \hat{n}\)이므로 단위 전하가 받는 힘은 항상 동일한 식으로 표현할 수 있다.

\[\therefore ~ \vec{f} = \frac{1}{2 \epsilon_{0}} \sigma^2 \hat{n}\]

• 내부가 비어있는 도체 내부의 전기장 또한 \(\vec{E}= \vec{0}\)이다.

[!question]- Why?{title} 어차피 안이 차있는 도체도 전하는 다 표면에 몰려있다. 따라서 안이 차있던 비어있던, 상황이 다르지 않다.

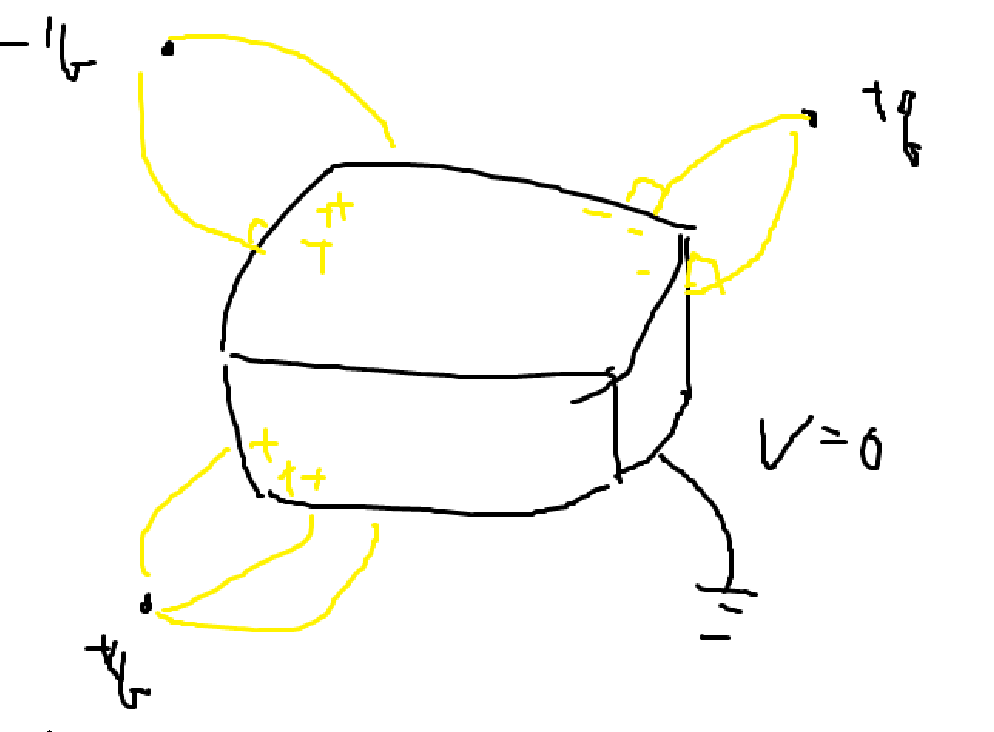
증명해보자. Consider. 내부가 비어있고, 접지해있는 도체 Box

이때 내부의 전기장을 구하는 것이 목표. 내부에 전하가 없으므로 라플라스 방정식 \(\nabla^2V = 0\)을 만족한다.

Boundry Condition은, 접지 상태이므로 표면에서 \(V=0\)이다. 찾을 수 있는 가장 간단한 해는, \(V=0\)이면 위 두 조건이 둘다 만족된다.

표면에서 전위가 주어지면, 그 내부의 전위값이 유일함이 보장되므로, 위 문제 상황에서 해는 유일하게 \(V=0\)으로 결정된다.

따라서 전기장 또한 \(\vec{0}\)이다.

Boundry Condition (경계 조건)

• \(\displaystyle E^{\bot}_{above} - E^{\bot}_{below} = \frac{\sigma}{\epsilon_{0}}\) : 전기장의 수직 성분은 불연속이다.
• \(\displaystyle E^{\parallel}_{above} - E^{\parallel}_{below}=0\) : 전기장의 수평 성분은 불연속이다.
• \(V_{above} - V_{below} = 0\) : 전위는 항상 연속이다.
• 도체가 지면과 접지하면 \(V=0\)이다.
• 보통 \(r\to \infty\)이면, \(V=0\)이다.

도체의 특성 때문에, 도체의 경계면에 의해서만 외부의 전기장이 결정된다. 경계면에 따라 전기장이 결정되기 때문에, 이를 경계 조건 (Boundry Condition)이라고 한다. 만약, 전기장이 면전하 \(\sigma\)를 갖는 경계면과 만나면 어떻게 될까?

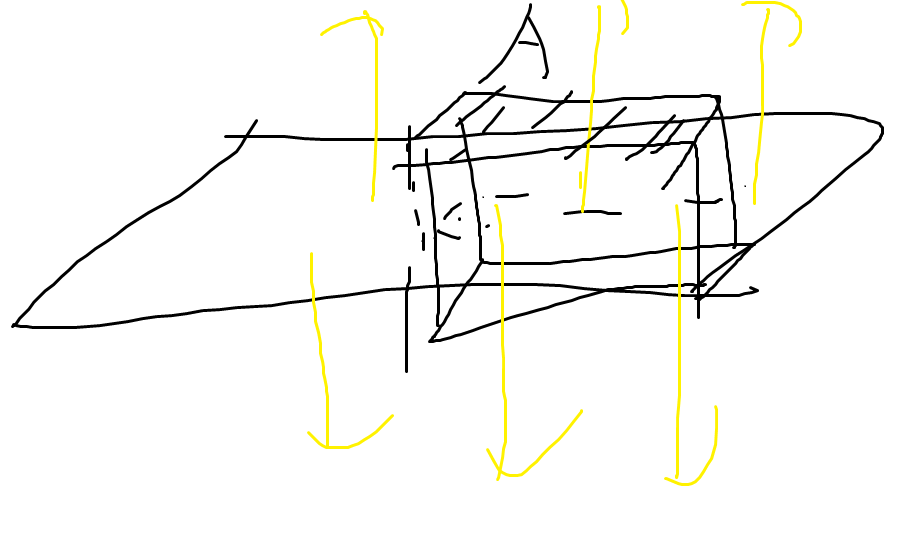
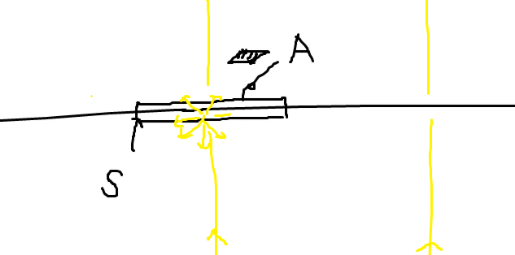
전기장의 수직 성분은, 곡면 위의 전기장과 아래의 전기장이 \(\displaystyle \frac{\sigma}{\epsilon_{0}}\)만큼 차이난다. 그 이유는 다음과 같다. 전하가 분포된 경계면을 아래에서 위로 전기장의 선속이 뚫고 나간다고 해보자. 동전 모양의 아주 얇고 경계면을 겹치는 가우스 곡면을 정의하자. 가우스 정리에 의해, 닫힌 곡면 내부에서 나오는 선속 (Flux)의 양은 내부 전하의 양으로 생각할 수 있다.

\[\oint_{S} \vec{E} \cdot d \vec{a} = E^{\bot}_{above} A - E^{\bot}_{below} A = \frac{Q_{inside}}{\epsilon_{0}} = \frac{{\sigma A}}{\epsilon_{0}}\] \[\therefore ~ E^{\bot}_{above} - E^{\bot}_{below} = \frac{\sigma}{\epsilon_{0}}\]

이때 side면은 아주 얇기 때문에 투과되는 Flux 양이 0이다. 따라서 전기장은 전하가 있는곳을 지나가면, 수직 성분은 불연속적이게 된다.

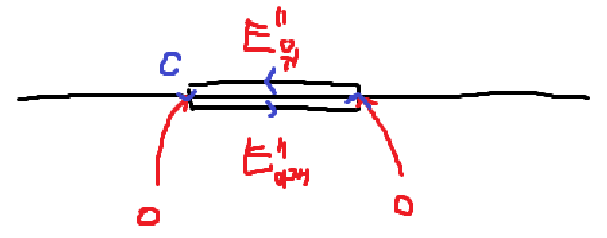
전기장의 평행 성분은, 곡면 위의 전기장과 아래의 전기장이 똑같다. 그 이유는 다음과 같다. 위와 같은 세로 폭이 아주 얇은 곡선 C를 잡아보자. 전기장에 대해 닫힌 경로 선적분한 결과는 항상 0이다. \(\displaystyle \oint_{C} \vec{E} \cdot d \vec{r} = 0\) 위 곡선은 수직 길이는 아주 얇기 때문에, 0과 같다. 따라서 적분을 하면, 위 전기장에서 l만큼 선적분한 것과 아래 전기장에서 l만큼 선적분한 것만 남는다.

\[\oint_{C} \vec{E} \cdot d \vec{r} = E^{\mid\mid}_{above}l - E^{\mid\mid}_{below}l = 0 \implies ~ E^{\mid\mid}_{above} - E^{\mid\mid}_{below}= 0\]

전위는 전위는 경계면에 관계없이 항상 연속이다.

\[V_{above} - V_{below} = - \int_{below}^{above} \vec{E} \cdot d\vec{r} \to 0\]

도체가 지면과 접지하면 \(V=0\)이다. 그 이유는 무엇인가? 지구는 하나의 거대한 도체다. 지구와 도체를 연결하면, (지구 + 도체)를 하나의 도체 덩어리로 간주한다. 도체 내부의 전위는 상수값이다. 보통 지구의 전위를 0으로 기준잡으므로, 연결한 도체의 전위도 0이다.

보통 \(r\to \infty\)이면, \(V=0\)이다. 하지만 특수한 케이스도 존재함.

[!example]- 특수 케이스 : 무한히 뻗은 가상의 Line Charge{title}

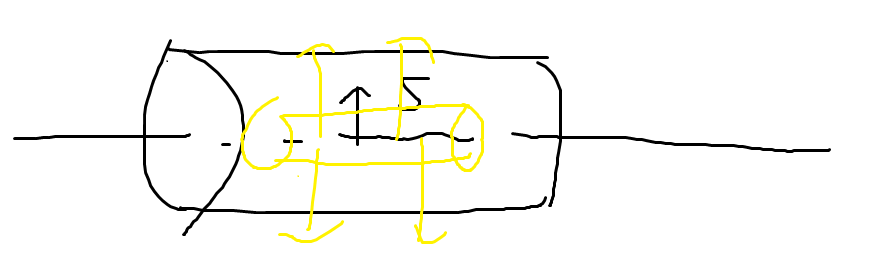
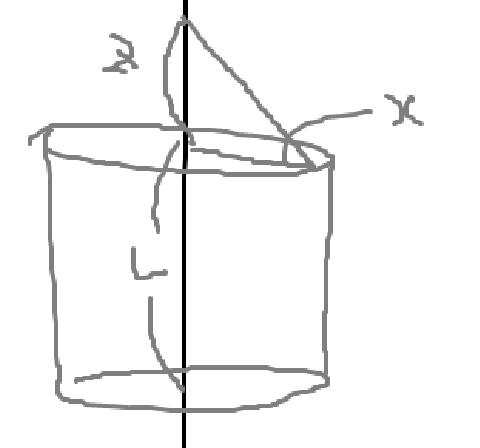
도선을 감싸는 길이가 L이고, 반지름이 x인 원통형 가우스 곡면을 정의해보자. 가우스 법칙에 따라 다음과 같다.

\[\oint_{S} \vec{E} \cdot d \vec{a} = \frac{q}{\epsilon_{0}} = \frac{\lambda L}{\epsilon_{0}}\]

위 가우스 곡면을 \(\vec{E}\) 면적분한 것은, 윗면과 밑면에 통과되는 전기장의 Flux는, 전기장을 상상해보면 0이라는걸 알 수 있다. 옆면을 통과하는 Flux 양은 대칭성을 가지므로, 전기장을 상수취급할 수 있다.

\[\oint_{S} \vec{E} \cdot d \vec{a} = E \oint_{S} d \vec{a}\]

\(\oint_{S} d \vec{a}\)는 원통 옆면의 넓이 \(2\pi xL\)과 같다.

\[E \cdot 2\pi xL = \frac{\lambda L}{\epsilon_{0}}\] \[\therefore ~ E = \frac{\lambda}{2\pi \epsilon_{0}} \frac{1}{x}\]

전위를 계산해보자. 계산하는 두가지 방법이 있다.

\[V(x) = -\int_{\infty}^{x} \vec{E} \cdot d \vec{r}\]

또는

\[E = - \nabla V =- \frac{dV}{dx} \implies dV = - E dx\] \[\implies V(x) - V(\infty) = -\int_{\infty}^{x} E dx'\] \[= - \int_{\infty}^{x} \frac{\lambda}{2\pi \epsilon_{0}} \frac{1}{x'} dx'\] \[= - \left[ \frac{\lambda}{2\pi \epsilon_{0}} \ln \lvert x' \rvert \right]^x_{\infty} = \infty\]

전위가 어느 위치에서든 \(\infty\)이다? 말이 안된다.

왜 이런 결과가 나오는가?

암묵적으로 \(V(\infty) = 0\)이라고 정의하고 있는데, 무한히 긴 도선이 있다면 \(V(\infty) \neq 0\)이기 때문이다.

따라서,

\[V(x) - V(x_{0}) = - \left[ \frac{\lambda}{2\pi \epsilon_{0}} \ln \lvert x' \rvert \right]^x_{x_{0}}\] \[= - \frac{\lambda}{2\pi \epsilon_{0}}(\ln x - \ln x_{0})\] \[\therefore ~ V(x) = - \frac{\lambda}{2\pi \epsilon_{0}} \ln x + C\]