기초전자기학 19. 파동이란 무엇인가

파동이란 무엇인가?

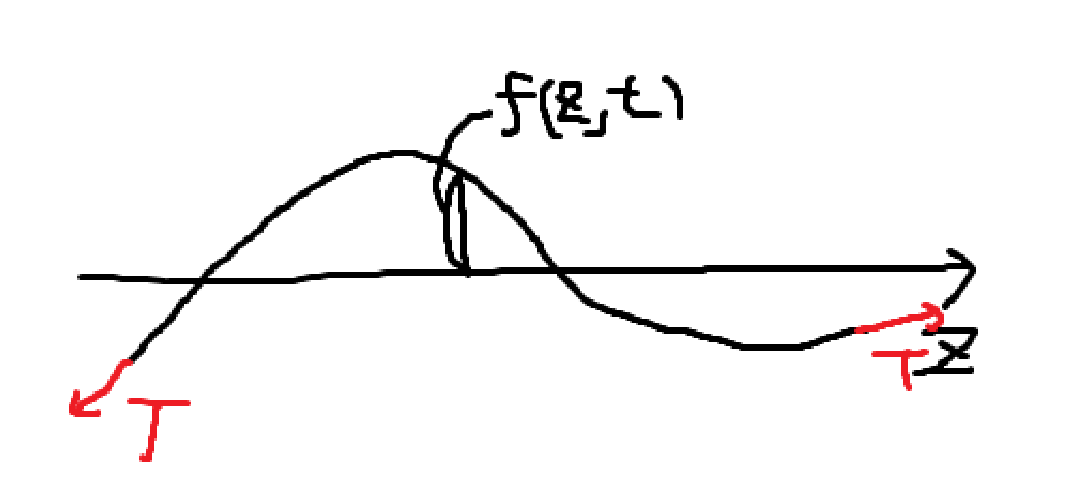
만약에 위치, 시간을 넣었을 때 그 지점에서의 파동의 변위(진폭)를 알려주는 함수가 있다면, 그 함수가 파동을 표현하고 있다고 볼 수 있을 것이다. 이 함수에 대한 방정식을 세워보자.

줄을 잡고 흔들면 파동이 생긴다. 파동이 생기는 원인은 장력이다. 파동의 한 지점에서의 합력을 계산하고, 뉴턴 방정식에 대입하면 되지 않을까?

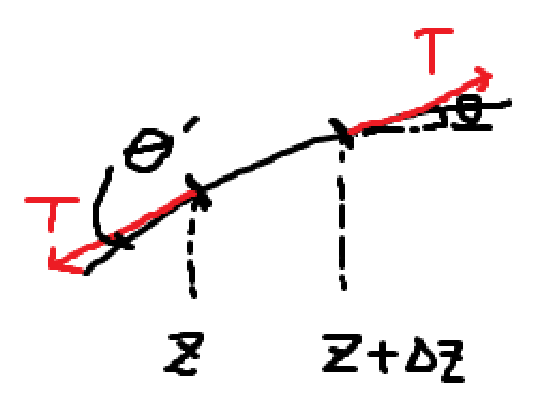
파동의 좁은 부분을 생각해보자. \(z, z+\Delta z\)를 계산하고 \(\Delta z\)를 0으로 보내면 파동의 한 지점의 정보를 알 수 있을 것이다.

우선, 해석적으로 풀기 위해 어떤 가정이 필요하다. \(\theta, \theta'\)가 아주 작아야 한다. 즉 앞으로 진폭 변화가 큰 파동은 기술하지 않을 것이다. 잔잔하게 요동치는 파동만을 고려하자.

\[\theta, \theta' \ll 1\]

중력 또한 고려하지 않고 파동에 대해서만 생각하자. 수평 방향의 장력은 상쇄된다.

\[T \cos \theta \simeq T \cos \theta' \simeq T\] \[T\cos \theta - T\cos \theta' \simeq 0\]

수직 방향의 장력은 다음과 같다.

\[T\sin \theta - T\sin \theta' \simeq T\tan \theta - T\tan \theta'\]

탄젠트는 기울기고, 기울기는 그 지점에서의 도함수 값과 같다.

\[= T \frac{\partial f(z,t)}{\partial z}\mid_{z+\Delta z} - T \frac{\partial f(z,t)}{\partial z}\mid_{z}\]

이것이 파동의 좁은 System의 합력이고, 이는 뉴턴방정식에 따라 \(ma\)와 같다.

\[= ma\]

파동의 단위 길이당 질량을 \(\mu\)로 정의한다. 가속도는 파동의 변위인 \(f(z,t)\)를 시간에 대해 두번 미분한 것과 같다.

\[\implies \mu \Delta z \frac{\partial^2 f}{\partial t^2}=T \frac{\partial f(z,t)}{\partial z}\mid_{z+\Delta z} - T \frac{\partial f(z,t)}{\partial z}\mid_{z}\] \[\implies \mu \frac{\partial^2f}{\partial t^2} = T(\frac{\partial f(z,t)}{\partial z}\mid_{z+\Delta z} - \frac{\partial f(z,t)}{\partial z}\mid_{z})\] \[\implies \lim_{ \Delta z \to 0 } \mu \frac{\partial^2f}{\partial t^2} = T\lim_{ \Delta z \to 0 }\frac{\left( \frac{\partial f(z,t)}{\partial z}\mid_{z+\Delta z} - \frac{\partial f(z,t)}{\partial z}\mid_{z} \right)}{\Delta z}\] \[\implies \mu \frac{\partial^2f}{\partial t} = T \frac{\partial^2f}{\partial z^2}\] \[\therefore ~~ \frac{\partial^2f}{\partial z^2} = \frac{1}{v^2} \frac{\partial^2f}{\partial t^2}\]

위 방정식이 바로 파동 방정식(wave equation) 이다. \(v\)는 다음과 같다.

\[v \equiv \sqrt{ \frac{T}{\mu} }\]

상수 \(v\)는 무엇을 의미할까?

\[[v] = \left[ \frac{kg \cdot m / s^2}{kg / m} \right]^{1/2} = \left[ \frac{m^2}{s^2} \right]^{1/2} = \left[ \frac{m}{s} \right]\]

\(v\)는 파동의 전파 속도를 의미한다. 파동의 전파 속도는 줄의 장력과 단위 길이당 줄의 무게가 결정하는구나!