기초전자기학 18. 전자기장이 각운동량도 가지고 있을까
전자기장이 각운동량도 갖고 있을까?
고전역학에서 각운동량은 다음과 같다.
\[\vec{L} = \vec{r} \times \vec{p}\]전자기장이 갖는 각운동량 밀도는 다음과 같다.
\[\vec{l} = \vec{r} \times \vec{g} = \epsilon_{0} \vec{r} \times (\vec{E} \times \vec{B})\]전자기장이 각운동량을 갖는다는 것을 보여주는 좋은 실험이 있다.
.jpg)
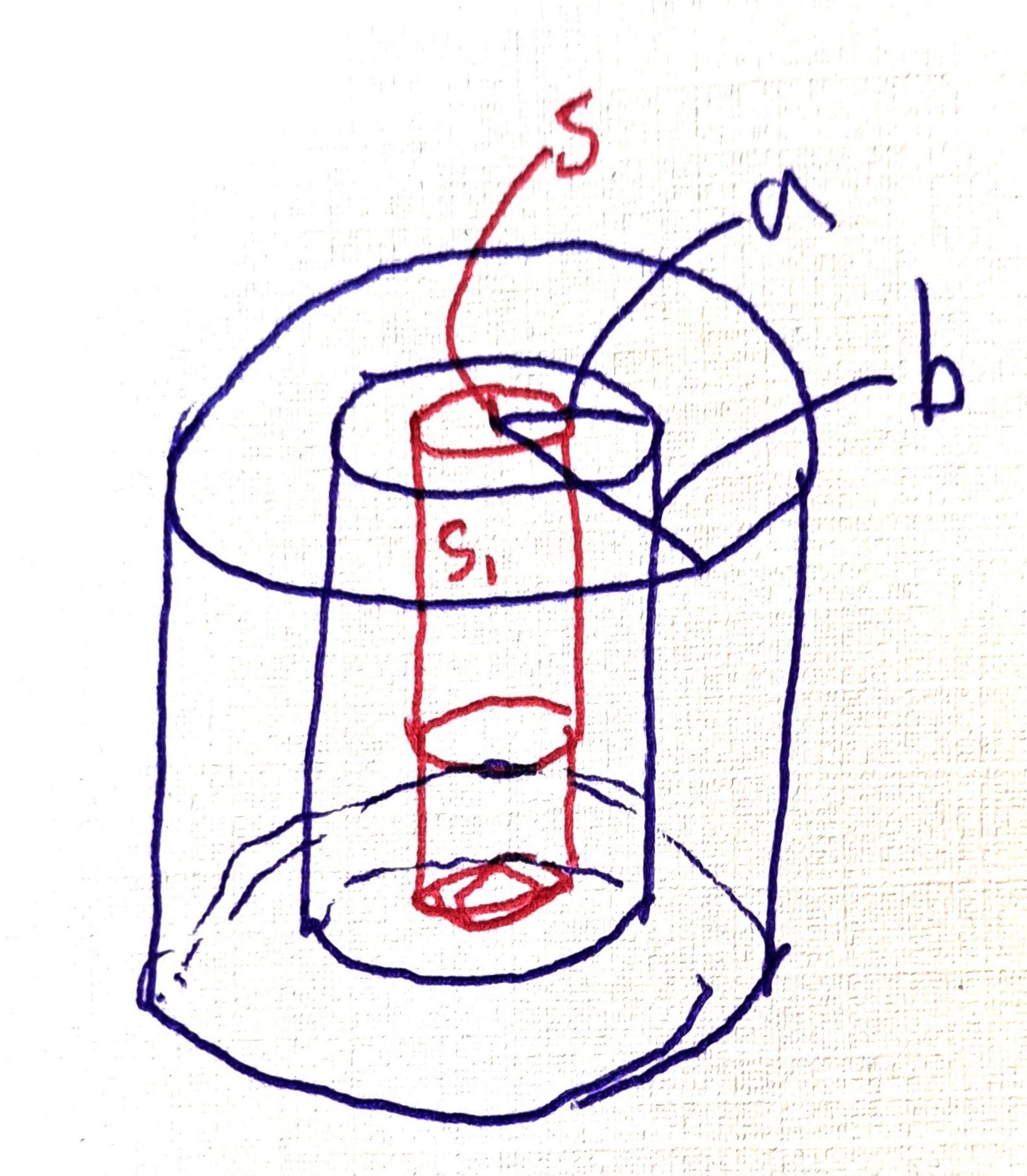
반지름이 R, 길이가 l, 길이당 감은 수 n인 솔레노이드에 전류 I를 흘리고 있다. 그 내부와 외부에 각각 반지름이 a, b이고 길이가 l이고 균일한 전하 +Q, -Q를 깔아둔 원통 껍질이 있다. 전류를 점점 줄이면 안팎에 있는 원통이 회전한다. 각운동량은 보존하는데, 아무것도 없어 보였던 각운동량이 어디서 생겼는가?: 전자기장이 갖고 있던 각운동량이 원통으로 이동한다.
전류를 줄이면 솔레노이드가 만드는 자기장의 세기가 줄고, 패러데이 법칙에 의해 원통 방향의 자기장을 만든다.. (1) 원통이 만들어 내는 유도 전기장이 반대쪽 원통에 힘을 가해 원통이 도는 Torque를 계산한다. 또, (2) 전자기장이 품고 있는 총 각운동량을 계산해서 비교해보자.
(1) 원통이 만들어 내는 유도 전기장이 반대쪽 원통에 힘을 가해 원통이 도는 Torque 패러데이 법칙에 의해 \(\hat{z}\) 방향으로 변하는 자기장은 \(\hat{\phi}\) 방향으로 전기장을 만들어낸다.
\[\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}\]솔레노이드에 수직한 반지름이 \(s\)인 앙페르 고리를 가정하자.
\[\implies \int_{S} \nabla \times \vec{E} \cdot d \vec{a} = - \frac{\partial}{\partial t} \int_{S} \vec{B} \cdot d \vec{a}\] \[\implies \oint_{C} \vec{E} \cdot d\vec{l} = - \frac{\partial}{\partial t}(\mu_{0}nI) \int_{S} d \vec{a}\]\(\int_{S} \vec{B} \cdot d \vec{a}\)는 자기 선속이고, 앙페르 고리를 통과하는 자기 선속은 앙페르 고리 반지름에 따라 달라지므로 case를 구분해야 한다.
(1-1) \(s<R\)
\[E \cdot2\pi s = - \mu_{0}n \frac{dI}{dt} \pi s^2\] \[\implies E = - \frac{1}{2} \mu_{0}n \frac{dI}{dt} s\](1-2) \(s>R\)
\[E \cdot2\pi s = - \mu_{0}n \frac{dI}{dt} \pi R^2\] \[\implies E = - \frac{1}{2} \mu_{0}n \frac{dI}{dt} \frac{R^2}{s}\]토크와 각운동량은 다음 식으로 계산한다.
\[\vec{N} = \vec{r} \times \vec{F} = \vec{r} \times (q\vec{E})\] \[= \vec{r} \times \frac{\partial \vec{p}}{\partial t} = \frac{\partial}{\partial t} (\vec{r} \times \vec{p}) = \frac{\partial \vec{L}}{\partial t}\]작은 원통이 받는 토크는 다음과 같다.
\[\vec{N}_{a} = \vec{r} \times \vec{E}(s)\] \[= a \hat{s} \times Q\left( -\frac{1}{2} \mu_{0}n \frac{dI}{dt}a \hat{\phi} \right)\] \[= - \frac{1}{2} \mu_{0}n a^2Q \frac{dI}{dt} \hat{z}\]그로 인해 생기는 각운동량의 변화량은 다음과 같다.
\[\frac{d\vec{L}_{a}}{dt} = - \frac{1}{2}\mu_{0}na^2Q \frac{dI}{dt} \hat{z}\] \[\implies \int \frac{d\vec{L}_{a}}{dt}dt = - \frac{1}{2} \mu_{0}na^2 Q \int \frac{dI}{dt}dt \hat{z}\] \[\implies \Delta \vec{L}_{a} = - \frac{1}{2}\mu_{0} na^2 Q \int_{I}^{0} dI \hat{z}\] \[= - \frac{1}{2}\mu_{0}na^2Q(-I)\hat{z}\] \[= \frac{1}{2}\mu_{0}na^2QI\hat{z}\]큰 원통이 받는 토크는 다음과 같다.
\[\vec{N}_{b} = \vec{r} \times \vec{E}(s)\] \[= b\hat{s} \times (-Q)\left( -\frac{1}{2}\mu_{0}n \frac{dI}{dt} \frac{R^2}{b} \hat{\phi} \right)\] \[= \frac{1}{2}\mu_{0}nR^2Q\frac{dI}{dt} \hat{z}\]그로 인해 생기는 각운동량의 변화량은 다음과 같다.
\[\frac{d\vec{L}_{b}}{dt} = \frac{1}{2}\mu_{0}nR^2Q \frac{dI}{dt} \hat{z}\] \[\implies \Delta \vec{L}_{b} = \frac{1}{2}\mu_{0} nR^2 Q \int_{I}^{0} dI \hat{z}\] \[= -\frac{1}{2}\mu_{0}nR^2QI\hat{z}\]전류가 0이 되었을 때 원통들이 갖는 총 각운동량은 다음과 같다.
\[\vec{L}_{total} = \Delta\vec{L}_{a} + \Delta\vec{L}_{b} = -\frac{1}{2}\mu_{0}nQI(R^2-a^2)\hat{z}\](2) 전자기장이 품고 있는 총 각운동량
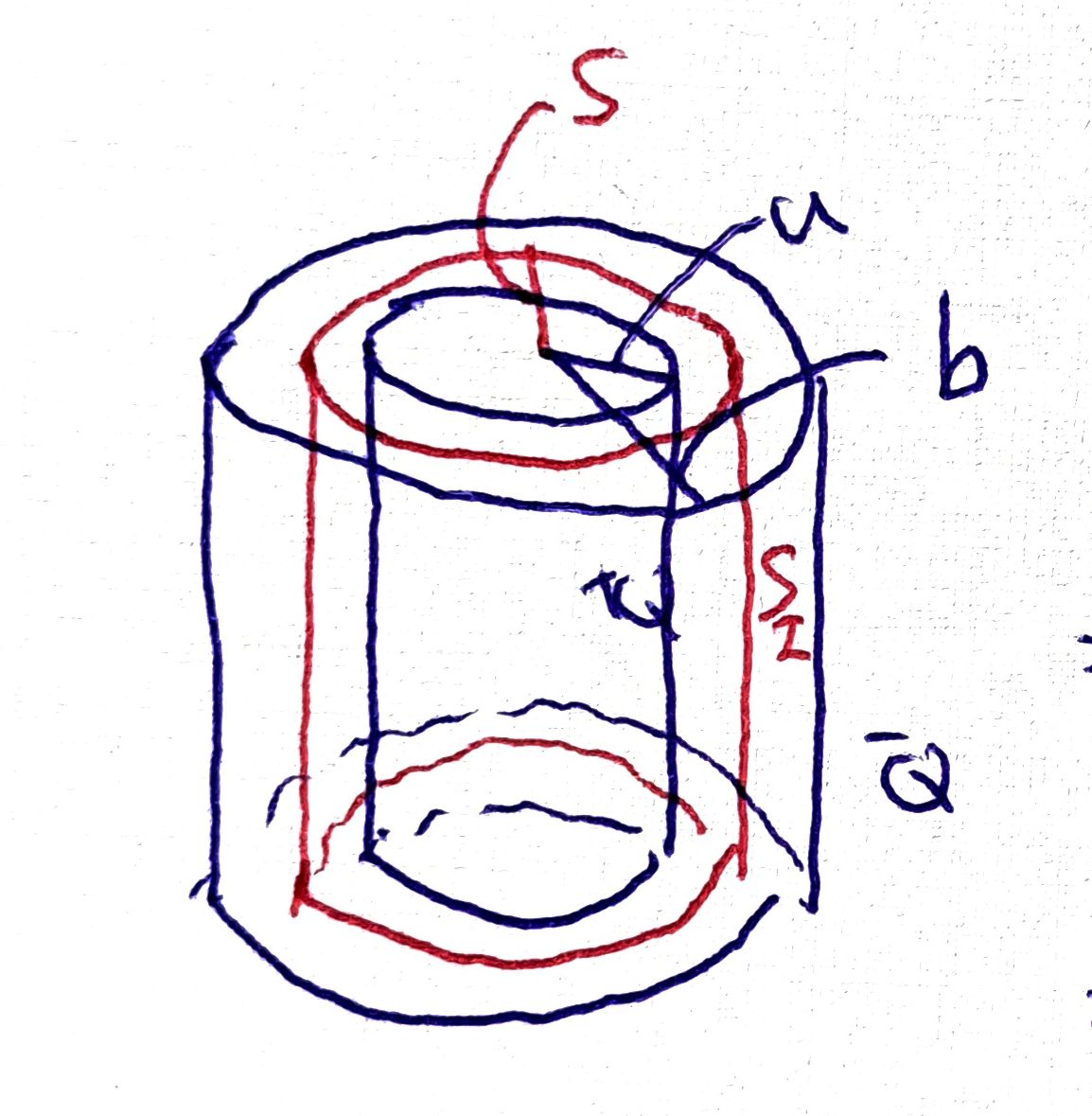
\[\vec{l} = \epsilon_{0} \vec{r} \times (\vec{E} \times \vec{B})\]자기장은 \(s<R\) 범위에서 \(\vec{B} = \mu_{0}nI \hat{z}\)임을 알고 있다. 전기장을 구해보자. 전하 분포가 대칭적이므로 가우스 법칙의 적분꼴을 이용해보자.
(2-1) \(s<a\) 
\(S_{1}\) 내의 전하는 0이고, 가우스 폐곡면 원통은 대칭적이다. 또한 폐곡면 뚜껑의 Flux는 0이므로 옆면만 고려하면 된다.
\[E\cdot 2\pi sl = 0 \implies E =0\](2-2) \(a<s<b\)
(2-3) \(s>b\)
따라서 전기장은 \(a<s<b\)일 때 \(\vec{E}=\frac{Q}{2\pi\epsilon_{0}l} \frac{1}{s} \hat{s}\)이다. 전기장과 자기장이 동시에 존재하는 구간은 \(a<s<R\)이고, 나머지 구간은 \(\vec{E} \times \vec{B}\) 값이 0이다.
\[\vec{l} = \epsilon_{0} \vec{r} \times (\vec{E} \times \vec{B})\] \[= \epsilon_{0}\vec{r} \times \left( \frac{Q}{2\pi\epsilon_{0}l} \frac{1}{s} \hat{s} \times \mu_{0}nI \hat{z} \right)\] \[= \frac{\mu_{0}nIQ}{2\pi ls} \vec{r} \times (-\hat{\phi})\]\(\vec{r} = r\hat{r} = s\hat{s} + z\hat{z}\)이다.
\[= - \frac{\mu_{0}nIQ}{2\pi ls} (s\hat{s} + z\hat{z}) \times \hat{\phi}\] \[= - \frac{\mu_{0}nIQ}{2\pi ls} (s\hat{z} - z\hat{s})\]이제 전자기장이 갖는 각운동량은 \(0<z<l\), \(a<s<R\) 범위에서 전자기장의 각운동량 밀도를 부피 적분하면 구할 수 있다.
\[\vec{L}_{em} = \int_{V} \vec{l} d\tau\] \[= \int_{V} - \frac{\mu_{0}nIQ}{2\pi ls} (s\hat{z} - z\hat{s}) d\tau\] \[= -\frac{\mu_{0}nIQ}{2\pi l} \int_{V} d\tau \hat{z} + \frac{\mu_{0}nIQ}{2\pi l} \int_{V} \frac{z}{s} \hat{s} d\tau\]\(\hat{z}\)는 \(s, z, \phi\) 성분이 바뀌든 말든 고정값이므로 적분 밖으로 나올 수 있다. \(\hat{s}\)는 \(\phi\)가 바뀌면 변하는 값이므로 적분 밖으로 나올 수 없다. 이를 주의하라.
\[= -\frac{\mu_{0}nIQ}{2\pi l} \pi l(R^2-a^2) \hat{z} + \frac{\mu_{0}nIQ}{2\pi l} \int_{0}^{2\pi}\int_{0}^l \int_{a}^R \left( \frac{z}{s} \hat{s} \right) s ds dz d\phi\]두번째 항의 적분값을 따로 계산해보자.
\[\int_{0}^{2\pi} \int_{0}^l \int_{a}^R \left( \frac{z}{s} \hat{s} \right) s ds dz d\phi = \left( \int_{0}^{2\pi} \int_{a}^{R} (s \cos \phi \hat{x} + s \sin \phi \hat{y}) ds d\phi \right)\left( \int_{0}^{l} z dz \right)\] \[= \left( \int_{a}^{R} s ds \right) \left( \frac{1}{2}l^2 \right)\left( \int_{0}^{2\pi} \cos \phi \hat{x} + \sin \phi \hat{y} d\phi \right)\] \[= \frac{1}{2} (R^2 - a^2) \cdot\frac{1}{2}l^2\cdot [\sin \phi \hat{x} - \cos \phi \hat{y}]^{2\pi}_{0}= 0\] \[\vec{L}_{em} = - \frac{1}{2} \mu_{0}nIQ (R^2-a^2)\hat{z}\]시간 0부터 T까지 원통에게 생긴 총 각운동량이, 전자기장이 품고 있던 각운동량과 동일하다.
\[\vec{L}_{total} = \vec{L}_{em}\]각운동량도 보존된다.
가우스 폐곡면의 모양을 어떻게 잡아야 할까?
\[\oint_{S}\vec{E} \cdot d \vec{a} = \frac{Q_{in}}{\epsilon_{0}}\]위 가우스 법칙의 적분 형태를 활용하기 위해 가우스 폐곡면을 잘 잡으면 문제를 쉽게 풀 수 있다. 주로 쓰이는 가우스 폐곡면은 구, 원통, 직육면체, 얇고 납작한 원기둥 등이 있다. 가우스 면 위에서 전기장의 크기와 방향이 일정하다면 적분이 \(E \cdot A\)로 바뀐다.
대칭의 기준이 무엇인가? 그냥 딱봐도 전하가 분포하고 있는 모양이 대칭적이라면 전기장을 구할 때 가장 먼저 고려해야 할 방법이다.
이때 전하 \(Q\)는 페곡면 \(S\) 내의 부피 속 총 전하와 같다.