기초전자기학 17. 전자기학의 운동량 보존 법칙이 무엇인가
전자기학의 운동량 보존 법칙이 무엇인가?
고전역학의 운동량 보존 법칙이 무엇인가? 고립계의 알짜 외력이 0일 때, 계의 모든 운동량 변화량의 합이 0이라는 것이다.
\[\sum_{i} \frac{d \vec{p_{i}}}{dt} = 0\]물체가 받는 힘은, 그 물체의 운동량의 변화율과 같다.
\[\vec{F} = \frac{d \vec{p}_{mech}}{dt}\]따라서, 운동량 보존 법칙에 따르면 고립계 내부의 모든 합력이 0과 같아야 한다.
\[\sum_{i} \vec{F}_{i} = 0\]부호가 플러스인 두 전하 \(q_{1}, q_{2}\)를 각각 x, y축에 \(\vec{v}\)만큼의 속도로 움직이게 해보자. 그 경우 전기장은 대칭이다. 전하가 움직이고 있으므로 자기장을 만든다. 본인이 만든 자기장은 본인의 운동량 변화에 영향을 주지 못하므로, 다른 전하가 만든 자기장에 로렌츠 힘 \(\vec{v} \times \vec{B}\)만을 받는다. 방향을 계산하면, 위 그림과 같다. 모든 힘의 합력을 합쳐보면 운동량이 보존되지 않는다!
나머지 운동량은 어디로 갔을까? 전자기장이 가지고 있다. 에너지 보존 법칙에서 보았듯이, 전하끼리는 운동량이 보존되지 않는다. 보존되는 양은 (전자기장 + 전하)의 운동량이다.
전자기학의 운동량 보존 방정식 또한 세가지 항이 존재한다. (1) 전자기장이 전하에 가하는 힘 (에 의한 전하의 운동량 변화), (2) 전자기장 자체가 갖는 운동량, (3) 전자기파에 의해 퍼져나가는 운동량. 이를 각각 계산하여 방정식을 유도해보자.
(1) 전자기장이 전하에 가하는 힘 + (2) + (3) 전자기장이 단위 전하에 가하는 로렌츠 힘의 합력은 다음과 같다.
\[\vec{F} = \int dq (\vec{E} + \vec{v} \times \vec{B})\]\(dq = \rho d\tau\)이므로, 부피 적분으로 바꾼다.
\[= \int_{V} (\vec{E} + \vec{v} \times \vec{B}) \rho d\tau\] \[= \int_{V} (\rho \vec{E} + \vec{J} \times \vec{B}) d\tau\]단위 부피 속 전하가 받는 힘은 \(\rho \vec{E} + \vec{J} \times \vec{B}\)와 같다.
\[\vec{f} = \rho \vec{E} + \vec{J} \times \vec{B}\]\(\rho\)와 \(\vec{J}\)를 가우스 (\(\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}}\)), 암페어-맥스웰 법칙 (\(\nabla \times B = \mu_{0} \vec{J} + \mu_{0} \epsilon_{0} \frac{\partial \vec{E}}{\partial t}\))을 사용하여 교체한다.
\[= \epsilon_{0}(\nabla \cdot \vec{E})\vec{E} + \left( \frac{1}{\mu_{0}} \nabla \times \vec{B} - \epsilon_{0} \frac{\partial \vec{E}}{\partial t} \right) \times \vec{B}\] \[= \epsilon_{0}(\nabla \cdot \vec{E})\vec{E} + \frac{1}{\mu_{0}} (\nabla \times \vec{B})\times \vec{B} - \epsilon_{0} \frac{\partial \vec{E}}{\partial t} \times \vec{B}\]\(\frac{\partial}{\partial t}(\vec{E} \times \vec{B}) = \frac{\partial \vec{E}}{\partial t} \times \vec{B} + \vec{E} \times \frac{\partial \vec{B}}{\partial t}\)와 패러데이 법칙 \(\nabla \times \vec{E} = -\frac{\partial \vec{B}}{\partial t}\)을 대입한다.
\[= \epsilon_{0} (\nabla \cdot \vec{E})\vec{E} + \frac{1}{\mu_{0}}(\nabla \times \vec{B})\times \vec{B}- \epsilon_{0}\left( \frac{\partial}{\partial t}(\vec{E} \times \vec{B}) + \vec{E} \times (\nabla \times \vec{E}) \right)\] \[= \epsilon_{0}((\nabla \cdot \vec{E})\vec{E} - \vec{E} \times (\nabla \times \vec{E})) + \frac{1}{\mu_{0}}(-\vec{B} \times (\nabla \times \vec{B})) - \epsilon_{0} \frac{\partial}{\partial t}(\vec{E} \times \vec{B})\]대칭성을 맞추기 위해 \(\frac{1}{\mu_{0}}(\nabla \cdot \vec{B})\vec{B}\)를 더하자. \(\nabla \cdot \vec{B} = 0\)이기 때문에 문제되지 않는다.
\[= \epsilon_{0}((\nabla \cdot \vec{E})\vec{E} - \vec{E} \times (\nabla \times \vec{E})) + \frac{1}{\mu_{0}}((\nabla \cdot \vec{B})\vec{B}-\vec{B} \times (\nabla \times \vec{B})) - \epsilon_{0} \frac{\partial}{\partial t}(\vec{E} \times \vec{B})\]\(\vec{E} \times (\nabla \times \vec{E})\)와 \(\vec{B} \times (\nabla \times \vec{B})\)는 다음 규칙을 사용한다.
\[\vec{E} \times (\nabla \times \vec{E}) = \frac{1}{2} \nabla (E^2) - (\vec{E} \cdot \nabla)\vec{E}\] \[\vec{B} \times (\nabla \times \vec{B}) = \frac{1}{2} \nabla (B^2) - (\vec{B} \cdot \nabla)\vec{B}\][!question]- Why?{title}
\[(\vec{A} \times (\nabla \times \vec{A}))_{i} = \sum_{j,k}\epsilon_{ijk} \vec{A}_{j} (\nabla \times \vec{A})_{k}\] \[= \sum_{j,k} \epsilon_{ijk} A_{j} \sum_{l,m} \epsilon_{klm} \partial_{l} A_{m}\] \[= \sum_{j,k,l,m} \epsilon_{kij} \epsilon_{klm} A_{j} \partial_{l} A_{m}\] \[= \sum_{j} (\delta_{il} \delta_{jm} - \delta_{im} \delta_{jl}) A_{j} \partial_{l} A_{m}\] \[= \sum_{j} (A_{j} \partial_{i} A_{j} - A_{j} \partial_{j} A_{i})\] \[= \sum_{j} \left( \frac{1}{2} \partial_{i} A_{j}^2 - A_{j} \partial_{j} A_{i}\right)\] \[= \frac{1}{2} \partial_{i} \vec{A}^2 - (\vec{A} \cdot \nabla)A_{i}\] \[\therefore ~~ \vec{A} \times (\nabla \times \vec{A}) = \frac{1}{2} \nabla(\vec{A}^2) - (\vec{A} \cdot \nabla)\vec{A}\]
이 결과를 그대로 대입한다.
\[= \epsilon_{0}\left( (\nabla \cdot \vec{E})\vec{E} + (\vec{E} \cdot \nabla)\vec{E} - \frac{1}{2}\nabla (E^2) \right) + \frac{1}{\mu_{0}}\left( (\nabla \cdot \vec{B})\vec{B} + (\vec{B} \cdot \nabla)\vec{B} - \frac{1}{2} \nabla(B^2) \right) - \epsilon_{0} \frac{\partial}{\partial t}(\vec{E} \times \vec{B})\]\(S= \frac{1}{\mu_{0}} \vec{E} \times \vec{B}\)였으므로, 뒤의 항은 \(-\epsilon_{0}\mu_{0} \frac{\partial \vec{S}}{\partial t}\)다. 이 항은 어떤 의미가 존재하는 것 같다. 하지만 앞에 항이 너무 복잡하다. 이 복잡한 항을 한큐에 표현하는 방법이 존재한다! 맥스웰 변형력 텐서 (Maxwell stress tensor)를 도입하면 된다.
\[T_{ij} \equiv \epsilon_{0} \left( E_{i}E_{j} - \frac{1}{2} \delta_{ij}E^2 \right) + \frac{1}{\mu_{0}}\left( B_{i} B_{j} - \frac{1}{2} \delta_{ij}B^2 \right)\]벡터는 아래 첨자가 하나인데, 텐서는 두개이므로 쌍방향 화살표 \(\overleftrightarrow{T}\)로 표기한다. \(\nabla \cdot \overleftrightarrow{T}\)는 복잡한 6개의 항을 한큐에 표현한다.
\[\vec{f} = \nabla \cdot \overleftrightarrow{T} - \epsilon_{0} \mu_{0} \frac{\partial \vec{S}}{\partial t}\]전자기장이 갖는 운동량 밀도를 다음과 같이 정의하자.
\[\vec{g} \equiv \epsilon_{0}\mu_{0}\vec{S} = \epsilon_{0}(\vec{E} \times \vec{B})\]따라서 다음과 같이 쓸 수 있다.
\[\vec{f} = \nabla \cdot \overleftrightarrow{T} - \frac{\partial \vec{g}}{\partial t}\]다시, \(V\)속의 모든 전하가 받는 총 힘을 생각해보자.
\[\vec{F} = \oint_{S} \overleftrightarrow{T} \cdot d \vec{a} - \frac{\partial}{\partial t} \int_{V} \vec{g} d\tau\]그 힘은 \(V\) 속의 모든 전하의 운동량의 변화량과 같다.
\[\vec{F} = \frac{\partial\vec{p}_{mech}}{\partial t} =\oint_{S} \overleftrightarrow{T} \cdot d \vec{a} - \frac{\partial}{\partial t} \int_{V} \vec{g} d\tau\]우변의 두번째 항은 전자기장의 운동량 밀도를 부피 \(V\)만큼 적분하고 있으므로, 부피 \(V\) 내의 전자기장이 갖는 총 운동량과 같다.
\[\vec{p}_{em} \equiv \int_{V} \vec{g} d\tau\]따라서 다음과 같이 방정식을 기술할 수 있다.
\[\frac{\partial(\vec{p}_{mech} + \vec{p}_{em})}{\partial t} + \oint_{S} (-\overleftrightarrow{T}) \cdot d\vec{a}= 0\]위 방정식의 해석은 ‘(총 전하 + 전자기장)의 운동량 변화는 경계면 \(S\)를 기준으로 유출되거나 유입되는 운동량과 같다’ 이다. 이것이 전자기 운동량에 대한 연속 방정식이다. 저 텐서는 두가지 물리적 의미가 있다. \(\overleftrightarrow{T}\)는 경계면 S에 가하는 층밀림힘이고, \(-\overleftrightarrow{T}\)는 \(\vec{J}\) 또는 \(\vec{S}\)과 같이 운동량의 흐름을 의미한다.
텐서란 무엇인가?
벡터는 크기와 방향을 갖는다. 텐서는 크기와 여러 방향성을 갖는다. 예를들어 2계계 텐서(rank-2 tensor) \(T_{ij}\)는 크기는 \(T_{ij}\)이지만 방향은 \(i\), \(j\)방향을 갖는다.
맥스웰 변형력 텐서가 무엇인가?
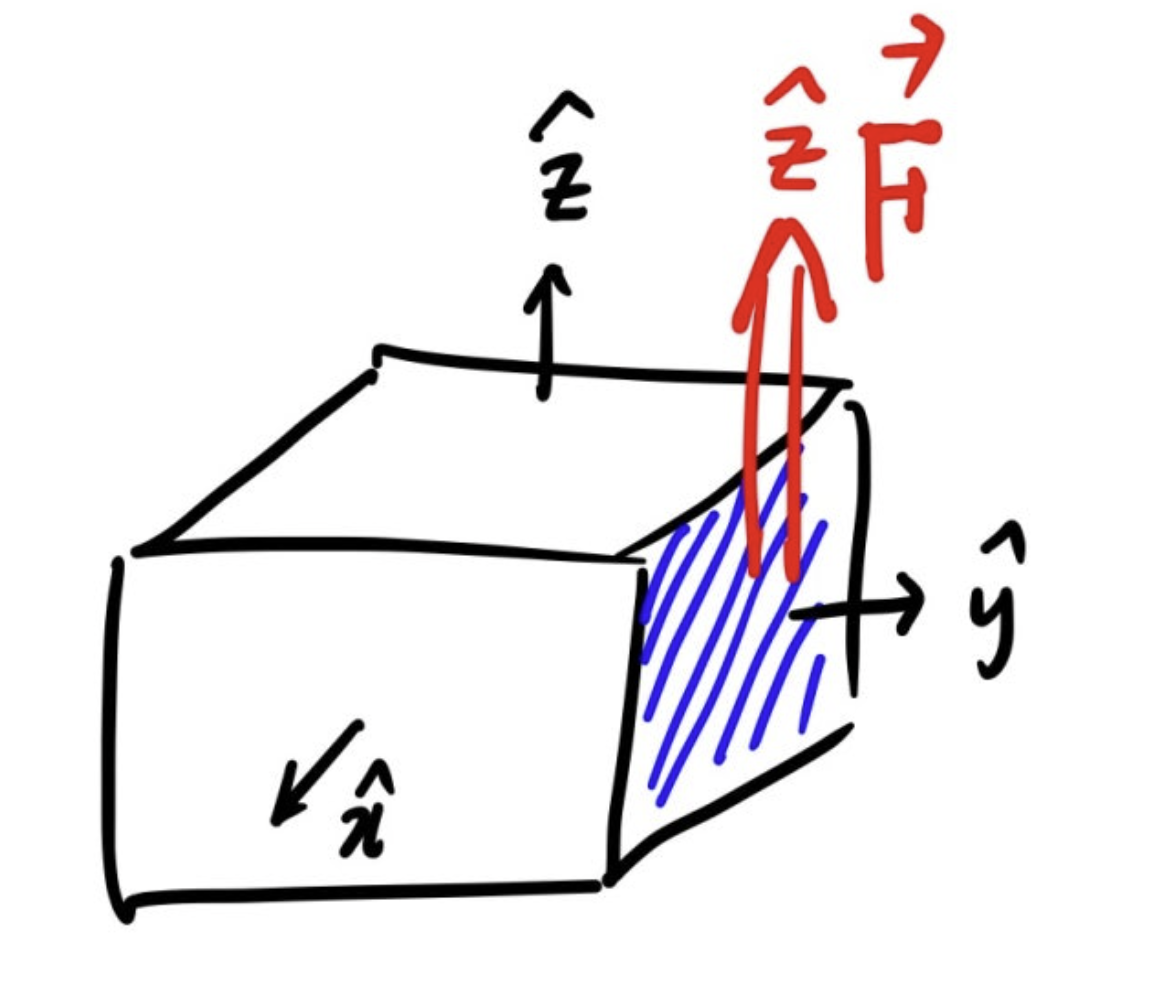
\[T_{ij}\]이것이 무슨 의미냐면, \(i\) 방향의 면에 \(j\) 방향으로 가해지는 힘을 의미한다. 즉 층밀림힘과 같다.
예를들어, \(T_{yz}\)는 위 그림처럼 \(y\) 방향 면에 \(z\) 방향으로 받는 힘의 양이다. \(T_{yz}>0\)이면, 물질이 다음과 같이 변형될 것이다.
하지만 위 방법은 구와 같이 방향이 다른 경우 적용하기 어렵다. 더 일반적으로 특정 지점에서 받는 층밀림힘을 계산하는 방법은 무엇인가?
해당 단위 면의 면적 벡터를 알면, 그 단위 면에 작용하는 층밀림힘을 계산할 수 있다.
\[\vec{t} = \overleftrightarrow{T} \cdot \hat{n}\]텐서 표기법을 사용하면 다음과 같다.
\[t_{i} = \sum_{j} T_{ij} n_{j}\]즉, \(t_{i}\)의 각각 성분을 계산하여 그 지점에서 받는 힘 벡터를 알 수 있다.
[!error] 텐서와 벡터의 점곱은 내적이 아니다!{title} 2계 텐서는 행렬이고, 텐서와 벡터의 곱은 행렬 벡터 곱과 같다. 내적이 아닌 이유는, 내적의 결과는 두 벡터 공간 위의 벡터를 내적하면 항상 어떤 체 \(F\) 위의 스칼라를 할당해야 하기 때문이다. 하지만 위 연산의 결과는 벡터이기 때문에, 내적이 아니다.
[!tip] 행렬 벡터 곱은 인덱스 표기법으로 표현하면 다음과 같다.{title}
\[(A\vec{v}) = \sum_{j}A_{ij}v_{j}\]
왜 맥스웰 변형력 텐서가 저 복잡한 식을 한큐에 표현하는가?
\[(\nabla \cdot \overleftrightarrow{T})_{i} = \sum_{k} \partial_{k}T_{ki}\] \[= \sum_{k}\partial_{k}\left( \epsilon_{0}\left( E_{k}E_{i}-\frac{1}{2} \delta_{ki} E^2 \right) + \frac{1}{\mu_{0}}\left( B_{k}B_{i} - \frac{1}{2} \delta_{ki} B^2 \right) \right)\] \[= \sum_{k} \left( \epsilon_{0} \left( \partial_{k}(E_{k}E_{i} ) - \frac{1}{2} \delta_{ki} \partial_{k} E^2 \right) + \frac{1}{\mu_{0}}\left( \partial_{k}(B_{k}B_{i}) - \frac{1}{2} \delta_{ki} \partial_{k} B^2 \right) \right)\]첫번째 항만 살펴보자.
\[\sum_{k}\epsilon_{0} \left( E_{i} \partial_{k} E_{k} + E_{k} \partial_{k}E_{i} - \frac{1}{2} \delta_{ki}\partial_{k}E^2 \right)\] \[= \epsilon_{0}\left( (\nabla \cdot \vec{E})E_{i} + (\vec{E} \cdot \nabla)E_{i} - \frac{1}{2} \partial_{i}E^2 \right)\] \[\implies \epsilon_{0}(\nabla \cdot \vec{E})\vec{E} + (\vec{E} \cdot \nabla)\vec{E} - \frac{1}{2}\nabla (E^2)\]이는 정확히 방정식의 세 항과 같다. 자기장항 또한 대칭이므로, \(\nabla \cdot \overleftrightarrow{T}\) 항이 복잡한 여섯개의 항을 한큐에 표현한다.
\(\nabla (\vec{A} \cdot \vec{B})\)를 어떻게 유도할까?
\[(\nabla(\vec{A} \cdot \vec{B}))_{i} = \partial_{i} (\vec{A} \cdot \vec{B})\] \[= \partial_{i} \sum_{j} A_{j}B_{j}\] \[= \sum_{j}( B_{j} \partial_{i}A_{j} + A_{j} \partial_{i}B_{j})\]핵심 아이디어는 다음과 같다: \(\partial\)과 미분된 항의 아래 첨자를 바꾼 값을 더하고 빼어 식을 조작해야 한다.
\[= \sum_{j}( (B_{j} \partial_{i} A_{j} + B_{j} \partial_{j} A_{i} - B_{j} \partial_{j} A_{i}) + (A_{j} \partial_{i} B_{j} + A_{j} \partial_{j} B_{i} - A_{j} \partial_{j} B_{i}))\] \[= (\vec{B} \cdot \nabla)A_{i} + (\vec{A} \cdot \nabla)B_{i} + \sum_{j}(B_{j}(\partial_{i} A_{j} - \partial_{j}A_{i}) + A_{j}(\partial_{i}B_{j} - \partial_{j}B_{i}))\]뒤 항은 \(\vec{B} \times (\nabla \times \vec{A})\)와 \(\vec{A} \times (\nabla \times \vec{B})\)와 관련있다. 그 이유는 다음과 같다.
\[(\vec{B} \times (\nabla \times \vec{A}))_{i} = \sum_{j,k} \epsilon_{ijk} B_{j} (\nabla \times \vec{A})_{k}\] \[= \sum_{j,k} \epsilon_{ijk} B_{j} \sum_{l,m} \epsilon_{klm} \partial_{l}A_{m}\] \[= \sum_{j,k,l,m} \epsilon_{kij}\epsilon_{klm} B_{j} \partial_{l} A_{m}\] \[= \sum_{j,k,l,m} (\delta_{il}\delta_{jm} - \delta_{im}\delta_{jl}) B_{j}\partial_{l}A_{m}\] \[= \sum_{j}(B_{j} \partial_{i} A_{j} - B_{j} \partial_{j} A_{o})\]정확히 세번째 항과 동일하다. 결론은 다음과 같다.
\[\therefore ~~\nabla (\vec{A} \cdot \vec{B}) = (\vec{B} \cdot \nabla)\vec{A} + (\vec{A} \cdot \nabla)\vec{B} + \vec{B} \times (\nabla \times \vec{A}) + \vec{A} \times (\nabla \times \vec{B})\].jpg)