기초전자기학 12. 맥스웰 방정식이 무엇인가

맥스웰 방정식이 무엇인가?

\[\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}}, ~\nabla \times \vec{E} = - \frac{\partial B}{\partial t}, ~\nabla \cdot \vec{B} = 0, ~\nabla \times \vec{B} = \mu_{0}\vec{J}\]

위 네개의 식이 지금까지 발견한 공식이다. 위 공식에는 모순이 존재한다.

\[\nabla \cdot (\nabla \times \vec{B}) = \mu_{0} \nabla \cdot \vec{J}\]

좌변은 반드시 0이지만, 우변은 steady current일 때만 0이다. 따라서, 우변이 항상 0이 되도록 상쇄하는 항을 하나 더 추가해야 한다. 연속방정식과 가우스 법칙을 사용해보자.

\[\nabla \cdot \vec{J} = - \frac{\partial \rho}{\partial t} = - \frac{\partial(\epsilon_{0} \nabla \cdot \vec{E})}{\partial t} = - \epsilon_{0} \nabla \cdot \frac{\partial \vec{E}}{\partial t}\]

즉, 앙페르 법칙을 다음과 같이 고친다.

\[\nabla \times \vec{B} = \mu_{0}\vec{J} + \mu_{0}\epsilon_{0}\frac{\partial \vec{E}}{\partial t}\]

새롭게 추가한 항을 대체 전류(displacement current)라고 부르지만, 좋은 이름은 아니다. 전류와 무관하기 때문이다.

완성된 맥스웰 방정식은 다음과 같다.

\[\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}}, ~\nabla \times \vec{E} = - \frac{\partial B}{\partial t}, ~\nabla \cdot \vec{B} = 0, ~\nabla \times \vec{B} = \mu_{0}\vec{J} + \mu_{0}\epsilon_{0} \frac{{\partial \vec{E}}}{\partial t}\]

물질 속의 맥스웰 방정식이 무엇인가?

만약 유전체(부도체) 외부에 전기장을 걸면, 원자에 구속된 전자들이 전기장의 +쪽으로 쏠린다. 그로 인해 유전체의 한쪽이 +, 한쪽이 -를 띄는 편극이 일어난다. 내부의 편극된 moment의 방향, 세기 등을 전기 편극밀도 \(\vec{P}\)로 나타낸다.

이번엔 물질에 자기장을 걸면, 전자의 스핀이 한쪽 방향으로 정렬된다. 어떻게 정렬되는지에 따라 상자성체, 반자성체, 강자성체 등으로 구분된다. 내부의 정렬된 moment의 방향, 세기 등을 자화 밀도 \(\vec{M}\)로 나타낸다.

핵심은 물질의 외부에 전기장 또는 자기장을 걸면 편극 밀도 \(\vec{P}\), \(\vec{M}\)가 생긴다는 것이다. 전기 편극 밀도 \(\vec{P}\)는 아래 공식 유도로 인해, 두개의 전하 분포로 해석될 수 있음을 밝혔다.

\[V(\vec{r}) = \frac{1}{4\pi\epsilon_{0}} \int_{V}\frac{\hat{\eta}}{\eta^2} \cdot \vec{P}(\vec{r}') d^3\vec{r}'= \frac{1}{4\pi\epsilon_{0}} \oint_{\partial V} \frac{1}{\eta} \vec{P} \cdot d\vec{a} - \frac{1}{4\pi\epsilon_{0}}\int_{V} \frac{1}{\eta} \nabla' \cdot \vec{P} d^3\vec{r}'\] \[\sigma_{b} = \vec{P} \cdot \hat{n}, ~~\rho_{b} = - \nabla' \cdot \vec{P}\]

자화 밀도 \(\vec{M}\) 또한 아래 공식 유도로 인해, 두개의 전류로 해석될 수 있음을 밝혔다.

\[\vec{A}(\vec{r}) = \frac{\mu_{0}}{4\pi} \int_{V} d^3\vec{r}' \vec{M} \times \frac{\hat{\eta}}{\eta^2} = \frac{\mu_{0}}{4\pi} \oint_{\partial V} \frac{1}{\eta} \vec{M} \times \hat{n} da + \frac{\mu_{0}}{4\pi} \int_{V} \frac{1}{\eta} (\nabla \times \vec{M}) d^3\vec{r}'\] \[\vec{K}_{b} = \vec{M} \times \hat{n}, ~ \vec{J}_{b} = \nabla \times \vec{M}\]

전기 편극 밀도와 자화 밀도가 존재하면, \(\rho\)는 \(\rho_{f} + \rho_{b}\) 두개를 고려해야 하며, \(\vec{J}\)는 \(\vec{J}=\vec{J}_{f} + \vec{J}_{b} + \vec{J}_{p}\) 세개를 고려해야 한다. \(\vec{J}_{p}\)는 또 뭐냐? 외부 전기장이 시간에 대해 변화가 존재하면 (\(\frac{\partial \vec{E}}{\partial t}\)) 전기 편극밀도 \(\vec{P}\) 또한 변하게 된다. 그로 인해 \(\rho_{b}\)가 움직이며, 그 효과로 발생하는 전류를 편극 전류 \(\vec{J}_{p}\)로 정의한다. dynamicelectric에선 이 편극 전류까지 고려한다.

\[\vec{J}_{p} = \frac{\partial \vec{P}}{\partial t}\]

아무튼, \(\rho\)과 \(\vec{J}\)가 여러개이므로 \(\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}}\)과 \(\nabla \times \vec{B} = \mu_{0}\vec{J} + \mu_{0}\epsilon_{0} \frac{{\partial \vec{E}}}{\partial t}\) 식이 복잡해진다. 이를 \(\vec{D}\)와 \(\vec{H}\)를 사용해서 간단히 나타내보자.

(1) 가우스 법칙

\[\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}} = \frac{1}{\epsilon_{0}}(\rho_{f} + \rho_{b}) = \frac{1}{\epsilon_{0}}(\rho_{f} - \nabla \cdot \vec{P})\] \[\implies \nabla \cdot (\epsilon_{0} \vec{E} + \vec{P}) = \rho_{f}\] \[\implies \nabla \cdot \vec{D} = \rho_{f}\]

(2) 앙페어-맥스웰 법칙

\[\nabla \times \vec{B} = \mu_{0}\vec{J} + \mu_{0}\epsilon_{0} \frac{\partial \vec{E}}{\partial t}\] \[= \mu_{0}(\vec{J}_{f} + \vec{J}_{b} + \vec{J}_{p}) + \mu_{0}\epsilon_{0} \frac{\partial \vec{E}}{\partial t}\] \[= \mu_{0} \left( \vec{J}_{f} + \nabla \times \vec{M} + \frac{\partial \vec{P}}{\partial t} \right) + \mu_{0}\epsilon_{0} \frac{\partial \vec{E}}{\partial t}\] \[\implies \nabla \times \left( \frac{\vec{B}}{\mu_{0}} - \vec{M} \right) = \vec{J}_{f} + \frac{\partial}{\partial t}(\epsilon_{0}\vec{E} + \vec{P})\] \[\implies \nabla \times \vec{H} = \vec{J}_{f} + \frac{\partial \vec{D}}{\partial t}\]

따라서 물질 속의 맥스웰 방정식은 다음과 같다.

\[\nabla \cdot \vec{D} = \rho_{f}, ~~\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}, ~~ \nabla \cdot \vec{B} = 0, ~~\nabla \times \vec{H} = \vec{J}_{f} + \frac{\partial \vec{D}}{\partial t}\]

이 방정식을 사용하려면, \(\vec{D}\)와 \(\vec{H}\)를 \(\vec{E}\)와 \(\vec{B}\)로 나타내는 물성 관계식(constitutive relations)을 덧붙여야 한다. 그것은 재료에 따라 달라지며, 선형 매질에선 다음과 같다.

\[\vec{P} = \epsilon_{0} X_{e} \vec{E}, ~~\vec{M} = X_{m} \vec{H}, ~~ \vec{D} = \epsilon \vec{E}, ~~ \vec{H} = \frac{1}{\mu} \vec{B}\]

이때 \(\epsilon\equiv\epsilon_{0}(1+X_{e})\)이고, \(\mu\equiv \mu_{0}(1+X_{m})\)이다. \(X_{e}\)과 \(X_{m}\)은 물질마다 다른 상수 값이다.

\(\vec{J}_{p}\)를 어떻게 유도하는가?

연속방정식을 사용한다.

\[\nabla \cdot \vec{J}_{p} + \frac{\partial \rho_{b}}{\partial t} = 0\] \[\implies \nabla \cdot \vec{J}_{p} = - \frac{{\partial \rho_{b}}}{\partial t} = \nabla \cdot \frac{\partial \vec{P}}{\partial t}\] \[\implies \vec{J}_{p} = \frac{\partial \vec{P}}{\partial t}\]

\(\vec{D}, \vec{H}\)의 경계 조건은 무엇인가?

맥스웰 방정식을 적분 꼴로 바꾸면, 각각의 식에서 경계 조건을 하나씩 얻을 수 있다. 경계 조건은 미분 방정식을 풀 때 반드시 필요하다.

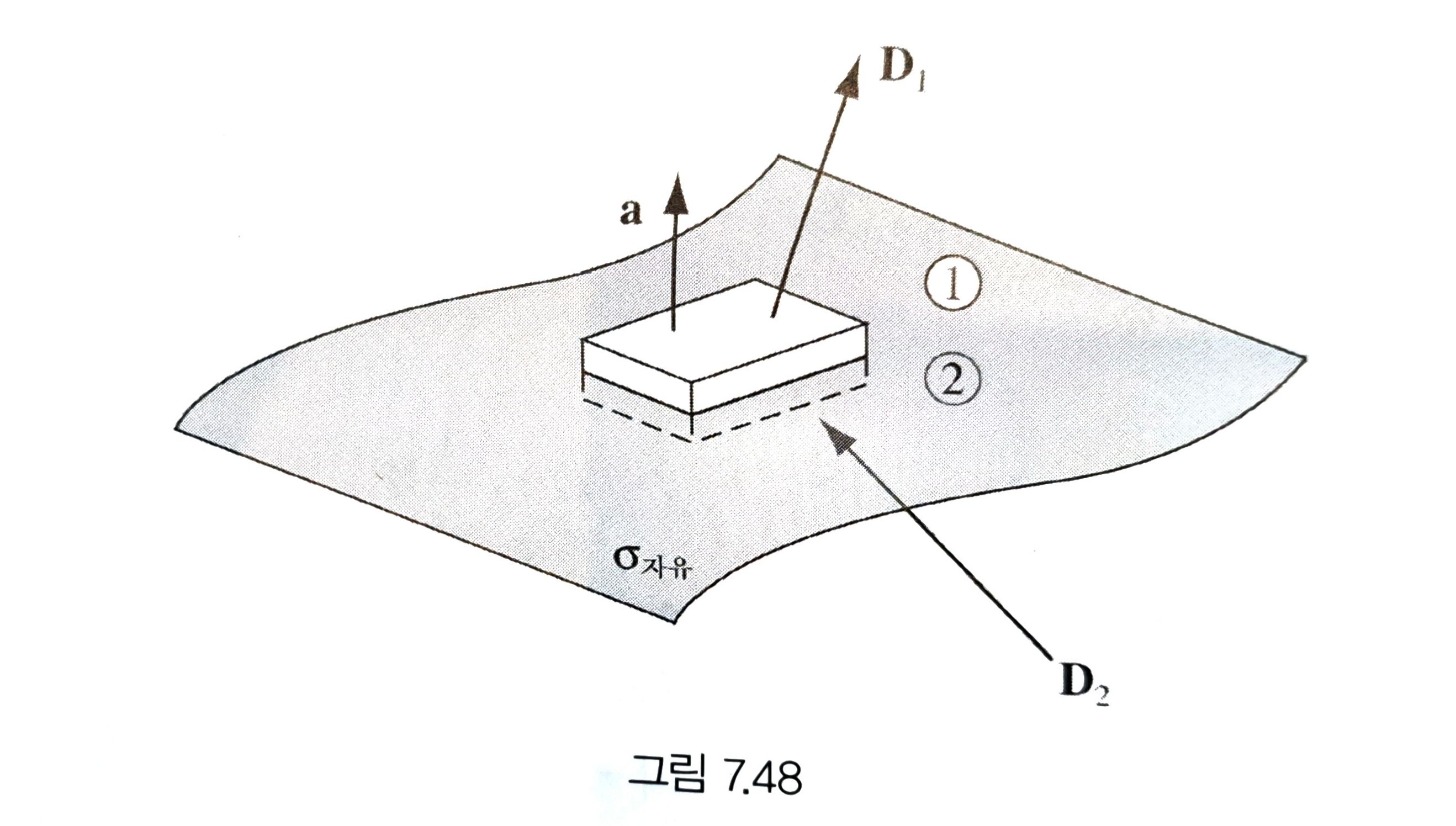
(1) \(\nabla \cdot \vec{D} = \rho_{f}\)

\[\int_{V} \nabla \cdot \vec{D} d\tau = \int_{V} \rho_{f} d\tau\] \[\implies \oint_{S} \vec{D} \cdot d\vec{a} = Q_{f,~in}\] \[\implies \vec{D}^{\text{above}} \cdot d \vec{a} - \vec{D}^{below} \cdot d \vec{a} =Q_{f, ~in}\] \[\implies D_{\bot}^{\text{above}} A-D_{\bot}^{\text{below}}A = \sigma_{f}A\] \[\implies D_{\bot}^{\text{above}}-D_{\bot}^{\text{below}} = \sigma_{f}\]

Free charge \(\rho_{f}\)가 존재하면, \(\vec{D}\)의 수직 성분은 불연속이다.

(2) \(\nabla \cdot \vec{B} = 0\)

\[\int_{V} \nabla \cdot \vec{B}d\tau = 0\] \[\implies \oint_{S} \vec{B} \cdot d \vec{a} = 0\] \[\implies \vec{B} ^{above} \cdot d \vec{a} - \vec{B}^{\text{below}} \cdot d \vec{a} = 0\] \[\implies B_{\bot}^{\text{above}}A - B_{\bot}^{\text{below}}A = 0\] \[\implies B_{\bot}^{\text{above}} = B_{\bot}^{\text{below}}\]

\(\vec{B}\)의 수직 성분은 항상 연속이다.

(3) \(\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}\)

\[\int_{S} (\nabla \times \vec{E}) \cdot d \vec{a} = \int_{S} \left( - \frac{\partial \vec{B}}{\partial t} \right) \cdot d \vec{a}\] \[\implies \oint_{C} \vec{E} \cdot d\vec{l} = - \frac{\partial}{\partial t} \int_{S} \vec{B} \cdot d \vec{a}\]

이때, 고리의 수직 길이가 0에 가까우므로, 면적 또한 0에 가깝다. 따라서, 자기장의 면적 Flux 값은 0이다.

\[\implies \vec{E}^{above} \cdot d\vec{l} - E^{\text{below}} \cdot d\vec{l} = 0\] \[\implies E_{\parallel}^{\text{above}}l - E_{\parallel}^{\text{below}}l = 0\] \[\implies E_{\parallel}^{\text{above}} = E_{\parallel}^{\text{below}}\]

\(\vec{E}\)의 평행 성분은 항상 연속이다.

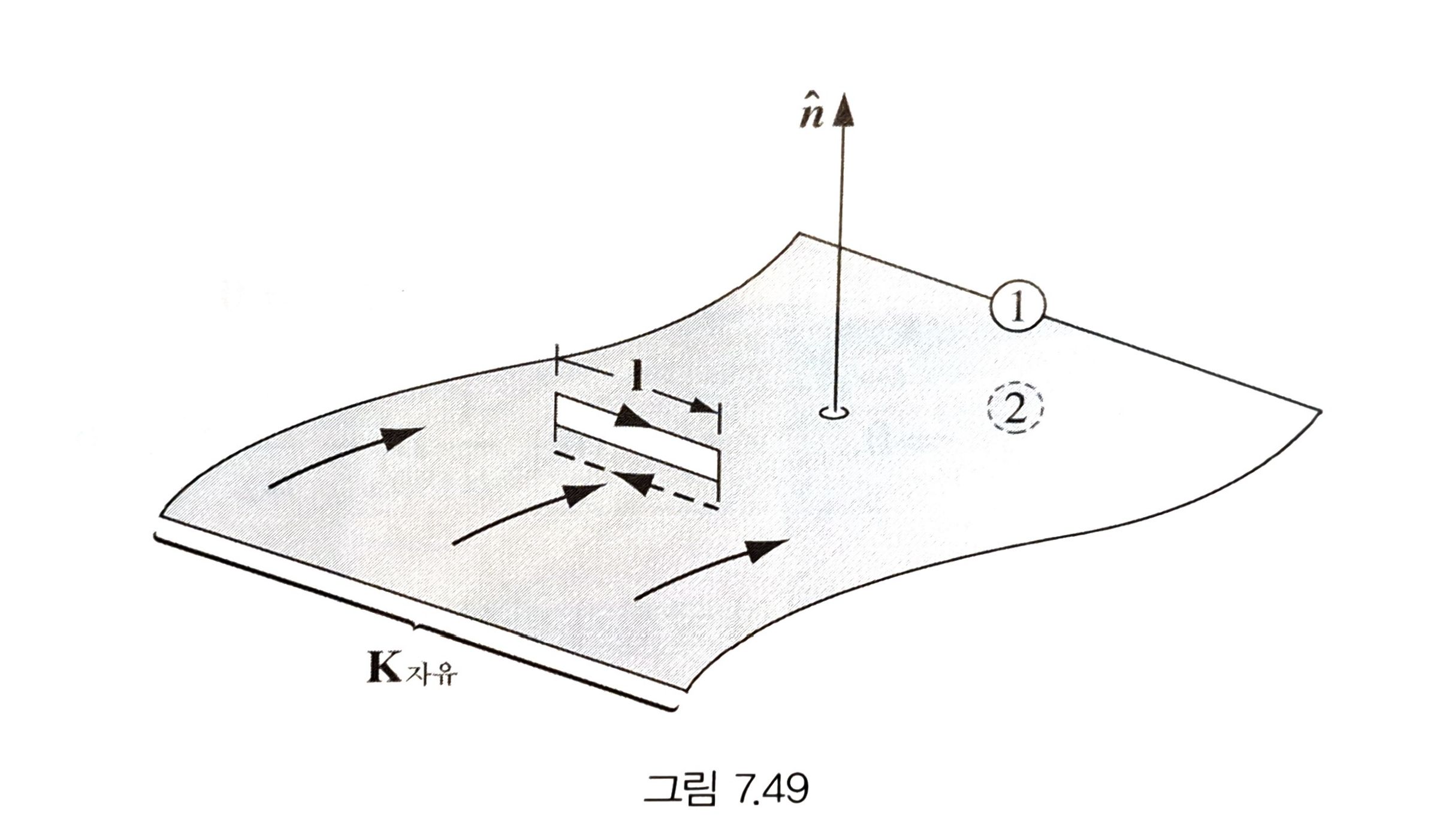
(4) \(\nabla \times \vec{H} = \vec{J}_{f} + \frac{\partial \vec{D}}{\partial t}\) \(\vec{K}_{f}\)와 수직한 앙페르 고리를 \(C_{1}\), 나란한 앙페르 고리를 \(C_{2}\)라고 하자.

\[\int_{S_{1}}(\nabla \times \vec{H}) \cdot d \vec{a} = \int_{S_{1}} \left( \vec{J}_{f} + \frac{\partial \vec{D}}{\partial t} \right) \cdot d \vec{a}\] \[\implies \oint_{C_{1}} \vec{H} \cdot d \vec{l} = \int_{S_{1}} \vec{J}_{f} \cdot d\vec{a} + \int_{S_{1}} \frac{\partial \vec{D}}{\partial t} \cdot d \vec{a}\]

\(I_{f, ~in}\)은 앙페르 고리 \(C\)를 지나는 자유 전류다. 세로 폭이 아주 작으므로, 면적을 지나는 \(\vec{D}\)는 0이다.

\[= \oint_{C_{1}} \vec{K}_{f} \cdot d\vec{l}\] \[\implies \vec{H}^{above} \cdot d \vec{l} - \vec{H}^{below} \cdot d \vec{l} = \vec{K}_{f} \cdot d\vec{l}\] \[\implies H^{above}_{\parallel} - H^{below}_{\parallel} = K_{f}\]

\(C_{2}\) 앙페르 고리를 사용하면, 앙페르 고리를 통과하는 자유 전류가 없다.

\[H^{above}_{\parallel} - H^{below}_{\parallel} = 0\]

앙페르 고리의 면적 벡터를 \(\hat{n}\)라고 하자. \(\hat{n}\)와 \(\vec{K}_{f}\)가 나란하면 \(K_{f}\), 수직하면 0이다. 따라서 외적으로 한번에 표현할 수 있다.

\[H^{above}_{\parallel} - H^{below}_{\parallel} = \vec{K}_{f} \times \hat{n}\]

Free current \(\vec{K}_{f}\)가 존재하면, \(\vec{H}\)의 평행 성분은 불연속이다.