기초전자기학 10. 패러데이 법칙이 무엇인가
기초전자기학 10. 패러데이 법칙이 무엇인가
패러데이 법칙이 무엇인가?
\[\nabla \times \vec{E} = - \frac{\partial \vec{B}}{\partial t}\](a) 실험에선 균일한 자기장 위에 일부만 걸친 도선을 움직이면 \(\varepsilon = - \frac{{\partial \Phi}}{\partial t}\)의 기전력이 생김을 보인다. (b) 실험에선 도선을 멈추고 자기장을 움직였을때도 똑같이 \(\varepsilon = - \frac{{\partial \Phi}}{\partial t}\)의 기전력이 생김을 보인다. 전하는 자기장에 의해 상대적으로 움직이기 때문에, 로렌츠 힘이 기전력을 만든다는 사실은 납득 가능하다. 정말 이상한 실험은 (c)다.
(c) 실험은 자기장을 변화시켰을 때 \(\varepsilon = - \frac{{\partial \Phi}}{\partial t}\) 기전력이 생겼다는 것이다. 선속 규칙으로 보면 이상할 것은 없다. 하지만 패러데이는 의문점을 가진다. 자기장과 전하는 모두 정지해있다. 정지해있는 전하를 움직일 수 있는 것은 전기장 밖에 없는데, 그 전기장은 어디서 오는가? 다음과 같은 결론을 도출한다:
\[\text{변화하는 자기장은 전기장을 만들어낸다.}\]따라서, 실험 (c)의 기전력의 원천은 유도된 전기장과 같다.
\[\varepsilon = \oint \vec{E} \cdot d\vec{l} = - \frac{\partial \Phi}{\partial t} = - \frac{\partial}{\partial t} \int_{S} \vec{B} \cdot d\vec{a} = - \int_{S} \frac{\partial \vec{B}}{\partial t} \cdot d\vec{a}\]스토크스 정리를 써서 정리하면 다음과 같다.
\[\int_{S} (\nabla \times \vec{E}) \cdot d\vec{a} = \int_{S} \left( - \frac{{\partial \vec{B}}}{\partial t} \right) \cdot d\vec{a}\] \[\implies \nabla \times \vec{E} = -\frac{ \partial \vec{B}}{\partial t}\]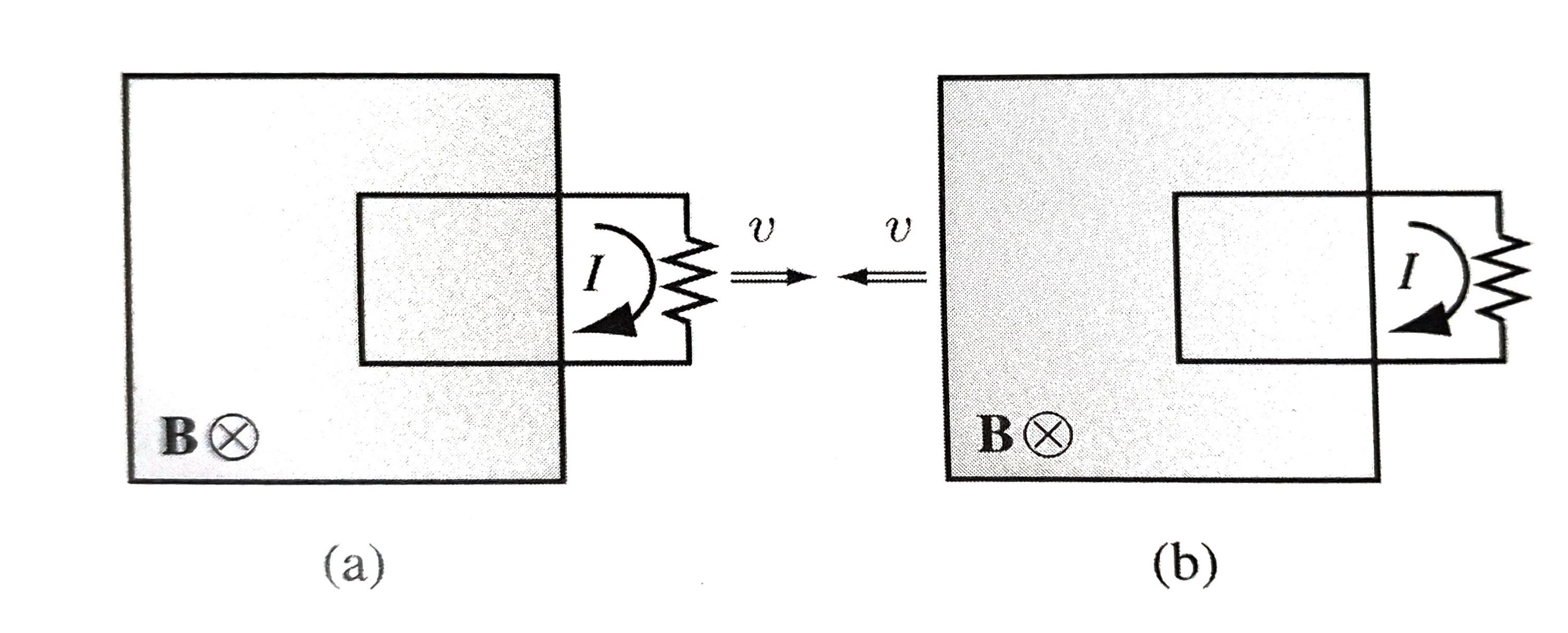
.jpg)